Factor the following trinomial: x2 + 8x + 15.
Answers
Answer:
(x + 3) (x + 5)
Related Questions
help me plz----------------------------

Answers
9514 1404 393
Answer:
A. 5 should have been subtracted in step 4
Step-by-step explanation:
No question is stated, so there is no "answer."
__
If we assume the question is, "What error did Keith make?" then choice A properly describes it.
Step 4 should look like ...
x -5 = 7y . . . . . . . 5 should be subtracted from both sides
and the final result should be ...
g(x) = (x -5)/7
What is 17,574 in expanded form?
Answers
Answer:
10,000 + 7,000 + 500 + 70 +4
Step-by-step explanation:
>
The following figure is made of 3 triangles and 1 rectangle!

Answers
The area for each part of the figure is given as follows:
Triangle A: 20 square units.Triangle D: 6 square units.Whole figure: 32 units squared.How to obtain the areas?The area of a right triangle is given by half the multiplication of it's sides.
Triangle A has the side lengths given as follows:
4 units.2 + 2 + 6 = 10 units.Hence the area is given as follows:
A = 0.5 x 4 x 10 = 20 units squared.
Triangle D is has the side lengths given as follows:
2 units 6 units.Hence the area is given as follows:
D = 0.5 x 2 x 6 = 6 units squared.
The total area is given by the sum of the areas of each part of the figure, hence:
20 + 2 + 4 + 6 = 32 units squared.
More can be learned about areas at https://brainly.com/question/21735282
#SPJ1
2 TO THE POWER OF 17 WHAT DA ANSWER
Answers
Answer:
131072
Step-by-step explanation:
Answer: The answer is 131072.
Step-by-step explanation:
Using a calculator, we find that \(2^{17}=\boxed{131072}.\)
A woman deposits $300 in a savings account that pays 6% annually. If she withdraws all the money in the account after 120 days, how much does she withdraw (rounded to the nearest dollar)?
Answers
The woman will withdraw $300 given 6% interest rate annually.
We can use the formula for simple interest to solve this problem:
I = Prt
where I is the interest earned, P is the principal (initial deposit), r is the annual interest rate as a decimal, and t is the time in years. Since the interest rate is given as an annual rate, we need to convert it to a daily rate by dividing by 365:
r = 0.06/365 = 0.00016438356
The time in years is 120/365 = 0.3287671233 years. Now we can plug in the values and solve for I:
I = 300 * 0.00016438356 * 0.3287671233 = 0.01699999999
The interest earned is $0.017, which is negligible. Therefore, the woman will withdraw the entire principal plus any interest earned, which is:
300 + 0.017 = $300.02
Rounding to the nearest dollar, the woman will withdraw $300.
To learn more about interest rate here:
https://brainly.com/question/29067327
#SPJ1
Amadi has jar with one dollar and two dollar coins in it.
There are coins in total.
A jar of one and two dollar coins.
The ratio of one dollar coins to two dollar coins is .
How many coins are two dollar coins
Answers
Without knowing the total number of coins or the ratio between one dollar and two dollar coins in the jar, we cannot accurately determine the number of two dollar coins.
Amadi has a jar with both one dollar and two dollar coins. The question is asking how many of the coins in the jar are two dollar coins.
To determine the number of two dollar coins, we need more information. The question does not provide any details about the total number of coins or the ratio between one dollar and two dollar coins in the jar. Without this information, it is not possible to give an accurate answer.
If we assume that the jar contains a total of 100 coins, we can use algebra to solve for the number of two dollar coins.
Let's say the number of two dollar coins is x. Then, the number of one dollar coins would be 100 - x.
Since the value of the two dollar coins is double the value of the one dollar coins, we can set up the equation 2x + 1(100 - x) = total value of coins.
Simplifying the equation, we get 2x + 100 - x = total value of coins.
Combining like terms, we have x + 100 = total value of coins.
Since we don't know the total value of coins, we cannot solve for x. Therefore, we cannot determine the number of two dollar coins without additional information.
For more such questions on dollar
https://brainly.com/question/30057220
#SPJ8
Triangle PQR has vertex coordinates at P(4, 0), Q(5, 4), R(5, 1). If the triangle is translated so that Q′(0, 4), determine the translation direction and number of units.
5 units down
5 units up
5 units to the right
5 units to the left
Answers
The translation direction is 5 units to the left.
To determine the translation direction and number of units, we can compare the original coordinates of point Q (Q(5, 4)) with the new coordinates of Q' after the translation (Q'(0, 4)).
By comparing the x-coordinates, we can see that the x-coordinate of Q' is smaller than the x-coordinate of Q, which means the triangle was translated to the left.
By comparing the y-coordinates, we can see that the y-coordinate of Q' is the same as the y-coordinate of Q, which means there was no vertical translation.
Therefore, the translation direction is 5 units to the left.
Learn more about Translation here:
https://brainly.com/question/11709244
#SPJ1
What is the measure of each interior angle of the regular polygon pictured below? If necessary, round to the nearest tenth.

Answers
\(\underset{in~degrees}{\textit{sum of all interior angles}}\\\\ n\theta = 180(n-2) ~~ \begin{cases} n=\stackrel{number~of}{sides}\\ \theta = \stackrel{degrees}{angle}\\[-0.5em] \hrulefill\\ n=5 \end{cases}\implies 5\theta =180(5-2) \\\\\\ 5\theta =180(3)\implies 5\theta =540\implies \theta =\cfrac{540}{5}\implies \theta =108\)
Geometry Support 4. Given: 6x-4 = 3x + 8. Prove: x = 4
Answers
Answer:
6(4)-4=3(4)+8
24-4=12+8
20=20
Step-by-step explanation:
To prove x=4, substitute four into the equation
6(4)-4=3(4)+8
24-4=12+8
20=20
Therefore x=4 is proved
Answer:
(Answer in Image)
Step-by-step explanation:
6x-4=3x+8
6x-4-3x=3x+8-3x subtract -3x on both sides
3x-4=8
3x-4+4=8+4 add four on both sides
3x=12 simplify
3/3x=12/3 divide both sides by 3
x=4

Suppose that a storm front is traveling at 33 mph. When the storm is 13 miles away a storm chasing van starts pursuing an average speed of 54 mph. How long does it take for the van to catch up with the storm? How far have they driven? (Hint: we can let our two variables be x= distance and t= time. Additionally, [speed x time= distance]. Won’t the van catch up when the distances are equal?
Please make it easy to understand your answer :)
Answers
Answer:
Time = X = 37.14 minutes
Distance they covered= 33.42 miles.
Step-by-step explanation:
Distance= speed * time
And the distance traveled by the two need to be equal.
Speed of storm = 33 mph
Speed of van = 54 mph
But storm is 13 miles away from van.
So
54*x = 33*x+ 13
54x-33x = 13
21x = 13
X= 0.62 hours
X = 37.14 minutes
54 *0.62= 33.42 miles.
help me fast rapidly is of khan academy:

Answers
Answer:
0 hundreds
0 tens
7 ones
.
4 tenths
0 hundredths
8 thousandths
Standard form=7.408
Step-by-step explanation:
Lets first solve (7x1)+(4x1/10)+(8x1/1000)
7+0.4+0.008
Simplify:
7.408
PLEASE MARK AS BRAINLIESTOn a blueprint, the length of a wall is 5 centimeters. If the actual length of the wall is 15 feet, what is the scale of the blueprint
Answers
Answer:
1 cm = 3 feet.
Step-by-step explanation:
Divide 15 by 5 to get 3; on the blueprint, every centimeter represents 3 feet.
The scale of scale factor of the blueprint is 1 cm = 3 feet.
What is a scale factor?The scale factor defines a variable in a ratio of two different measurements.
Sometimes drawings of large models are represented in a scale factor of a smaller unit.
Given, On a blueprint, the length of a wall is 5 centimeters and the actual length of the wall is 15 feet.
Therefore, The scale factor of the blueprint is,
= (5/15).
= 1/5.
So, It can be written as 1 cm = 3 feet.
learn more about scale factors here :
https://brainly.com/question/30215119
#SPJ2
4x + 5y = 7 3x – 2y = –12 Multiply each equation by a number that produces opposite coefficents for x or y
Answers
Answer:
Step-by-step explanation:
DO YOU MEAN :
\(4x + 5y = 7\\ 3x - 2y = -12\\Multiply-equation 1 -by -the-coefficient-of-x-in-equation-2\\multiply-equation-2 -by-the-co-efficient -of x -in-equation- 1\\\\3(4x + 5y = 7)\\4( 3x - 2y = -12)\\\\12x +15y=21\\12x -8y=-48\)
what are the assymptotes of this equation
Answers
Use a graphing tool to solve the equation below for x.
-3(-x) − 6 = -3x + 10
A. x ≈ -2.50
B. x ≈ 2.50
C. x ≈ -6.00
D. x ≈ -0.50
Answers
Answer:
C.
x ≈ 2.50
Step-by-step explanation:
The value of x in the given equation \(-3(-x) -6 = -3x+ 10\) is 2.66
What is a line graph?A line graph is a type of chart used to show information that changes over time. We plot line graphs using several points connected by straight lines. We also call it a line chart. The line graph comprises of two axes known as 'x' axis and 'y' axis. The horizontal axis is known as the x-axis.
According to the given question.
We have a equation
\(-3(-x)-6 = -3x +10\)
To draw a graph for the above equation we have to simplify the given equation.
Therefore,
\(-3(-x) -6 = -3x + 10\)
⇒ \(+3x-6 = -3x + 10\)
⇒\(3x+3x = 10 + 6\)
⇒ \(6x = 16\)
⇒ \(x = \frac{16}{6}\)
⇒ \(x = 2.66\)
After solving the above equation for x we have,
x = 2.66
⇒ A line which is parallel to y axis.
Therefore, we draw a line graph at a point x = 2.66 which is parallel to y axis.
Find out more information about line graph here:
https://brainly.com/question/23680294
#SPJ3

HELP WITH THIS MATH QUESTION PLS ^^ TY!

Answers
Answer:
volume of a brick: 10(7)(5) = 350 \(in^3\)
14000/350 = 40 bricks
4:20::8:x
What is x equal to?
Answers
May be May be
Hope it is correct
Which equation is equivalent to (1/3)^x=27^x+2?

Answers
3^-x = 3^3x+6 ... since the bases are the same, set the exponents equal
-x=3x+6..... move the variable to the left-hand side and change its side
-x-3x=6 ... collect like terms
-4x = 6..... divide both sides of the equation by -4 and I got x=-3/2
I don’t want this text to be that long so they both seem calculated the same way that’s why i got -3/2 hope that helps;-;
Compare the investment below to an investment of the same principal at the same rate compounded annually.
principal: $5,000, annual interest: 9%, interest periods: 4, number of years: 18
After 18 years, the investment compounded periodically will be worth $? more than the investment compounded annually.
(Round to two decimal places as needed.)
Answers
After 18 years, the investment compounded periodically (quarterly) will be worth $1,230.23 more than the investment compounded annually.
What is compounded interest?Compounded interest refers to the interest system that charges interest on both principal and accumulated interest.
The period of compounding in a year determines the worth of the future value.
The future value can be ascertained using an online finance calculator as follows:
Interest periods: = 4 times yearly (Quarterly)
Principal = $5,000
Annual interest rate = 9%
Number of years: 18
N (# of periods) = 72 quarters (18 years x 4)
I/Y (Interest per year) = 9%
PV (Present Value) = $5,000
PMT (Periodic Payment) = $0
Results:
Future Value (FV) = $24,815.83
Total Interest = $19,815.83
Interest periods: = Annually
N (# of periods) = 18 years
I/Y (Interest per year) = 9%
PV (Present Value) = $5,000
PMT (Periodic Payment) = $0
Results:
Future Value (FV) = $23,585.60
Total Interest = $18,585.60
Difference in Future Values $1,230.23 ($24,815.83 - $23,585.60)
Thus, an investment compounded periodically earns more than an investment compounded annually.
Learn more about compounded interest at https://brainly.com/question/28020457.
#SPJ1
-8/9 + (-2)/57
find the absolute value of the following rational number
Answers
The absolute value of the Rational number -474/513 is 474/513.
To find the sum of the rational numbers -8/9 and -2/57, you need to have a common denominator. The least common multiple (LCM) of 9 and 57 is 513. So, you can rewrite the fractions with a common denominator:
-8/9 = (-8/9) * (57/57) = -456/513
-2/57 = (-2/57) * (9/9) = -18/513
Now, you can add the fractions:
-456/513 + (-18/513) = (-456 - 18)/513 = -474/513
To find the absolute value of the rational number -474/513, you simply ignore the negative sign and take the value as positive:
| -474/513 | = 474/513
Therefore, the absolute value of the rational number -474/513 is 474/513.
For more questions on Rational .
https://brainly.com/question/30339525
#SPJ8
which expressions are equivalent to 3^4/9/3^2/9? select all that apply

Answers
Answer:
first and third expressions
Step-by-step explanation:
using the rule of exponents
\(\frac{a^{m} }{a^{n} }\) = \(a^{m-n}\)
then
\(\frac{3^{\frac{4}{9} } }{3^{\frac{2}{9} } }\)
= \(3^{\frac{4}{9}-\frac{2}{9} }\) ← first expression
= \(3^{\frac{2}{9} }\) ← third expression
You are given: (i) The future lifetimes of (40) and (50) are independent. (ii) The survival function for (40) is based on a constant force of mortality, u = 0.05. (iii) The survival function for (50) is So(x) = 1 - x/10 (De Moivre's Law with w=110). Calculate the probability that (50) dies within 10 years and dies after (40). A) Less than .02 B) At least .02 but less than .04 C) At least .04 but less than .06 D) At least .06 but less than .08 E) At least.08 Select one: A. Less than .02 B. At least .02 but less than .04 C. At least.04 but less than 06 D. At least.06 but less than 08 E. At least .08
Answers
The probability that (50) dies within 10 years and dies after (40) is at least 0.02 but less than 0.04. So the answer is B. At least .02 but less than .04.
To calculate the probability that (50) dies within 10 years and dies after (40), we need to find the joint probability of the two events happening together.
Let X and Y be the future lifetimes of (40) and (50), respectively. We want to find P(Y≤10 and X<Y). Using the Law of Total Probability, we can write:
P(Y≤10 and X<Y) = ∫P(Y≤10 and X<Y|X=t) fX(t)dt
where fX(t) is the probability density function of X.
Since the force of mortality for (40) is constant, the probability density function for X is given by:
f X (t)=ue −ut
where u=0.05.
For (50), we have the survival function S(y) = 1 - y/10. So, the probability density function for Y is:
fY(y) = S'(y) = 1/10
Now, we can substitute these expressions into the integral and simplify:
P(Y≤10 and X<Y) = ∫P(Y≤10 and X<Y|X=t) fX(t)dt
= ∫∫P(Y≤10 and X<Y|X=t) fY(y)fX(t)dydt
= ∫∫P(Y≤10 and t<Y) (1/10)(0.05)e^(-0.05t)dydt
= (1/10)∫e^(-0.05t) ∫1≤y≤10 e^(0.1y) dydt
= (1/10)∫e^(-0.05t) (e - e^(-t/10)) dt
Evaluating this integral, we get:
P(Y≤10 and X<Y) ≈ 0.0286
Find out more about the Law of Total Probability
at brainly.com/question/14315459
#SPJ4
NEEED HELPPO!!!!!!!!

Answers
Answer:
p = 23
Step-by-step explanation:
using the rules of exponents
• \((a^m)^{n}\) = \(a^{mn}\)
• \(a^{m}\) × \(a^{n}\) = \(a^{(m+n)}\)
then
\((x^3)^{5}\) (\(x^{8}\) )
= \(x^{3(5)}\) × \(x^{8}\)
= \(x^{15}\) × \(x^{8}\)
= \(x^{(15+8)}\)
= \(x^{23}\)
= \(x^{p}\) ← with p = 23
Hello can anyone pls help with this multiple choice question
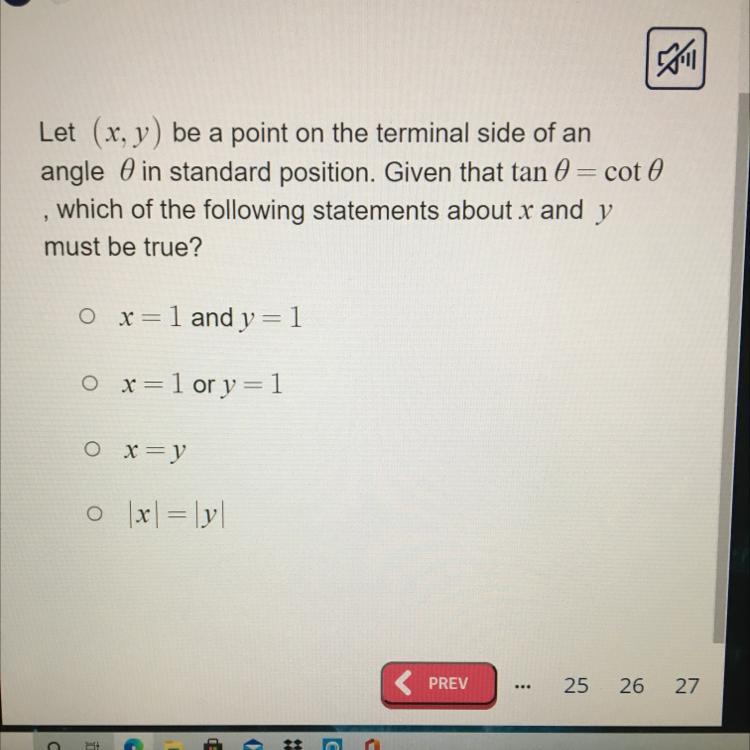
Answers
Answer:
The correct answer is the last one
Step-by-step explanation:
State the domain and range of the following function. {(6,-8), (9,3), (-3,5), (1,-6), (5,7)}

Answers
Answer:
Domain { -3,1,5,6,9}
Range { -8,-6,3,5,7}
Step-by-step explanation:
The domain is the inputs
Domain { 6,9,-3,1,5}
We normally put them in order from smallest to largest
Domain { -3,1,5,6,9}
The range is the outputs
Range { -8,-6,3,5,7}
The domain is the set of all x-coordinates.
So here, the domain is {6, 9, -3, 1, 5} which we
can write in ascending order as {-3, 1, 5, 6, 9}.
Note that the domain is usually written in ascending order.
In other words, from least to greatest.
Next, the range is the set of all y-coordinates.
So here, the range is {-8, 3, 5, -6, 7} which we
can write in ascending order as {-8, -6, 3, 5, 7}.
Like the domain, the range is usually written in ascending order.
How can i prove this property to be true for all values of n, using mathematical induction.
ps: spam/wrong answers will be reported and blocked.

Answers
Proof -
So, in the first part we'll verify by taking n = 1.
\( \implies \: 1 = {1}^{2} = \frac{1(1 + 1)(2 + 1)}{6} \)
\( \implies{ \frac{1(2)(3)}{6} }\)
\(\implies{ 1}\)
Therefore, it is true for the first part.
In the second part we will assume that,
\( \: { {1}^{2} + {2}^{2} + {3}^{2} + ..... + {k}^{2} = \frac{k(k + 1)(2k + 1)}{6} }\)
and we will prove that,
\(\sf{ \: { {1}^{2} + {2}^{2} + {3}^{2} + ..... + {k}^{2} + (k + 1)^{2} = \frac{(k + 1)(k + 1 + 1) \{2(k + 1) + 1\}}{6}}}\)
\( \: {{1}^{2} + {2}^{2} + {3}^{2} + ..... + {k}^{2} + (k + 1)^{2} = \frac{(k + 1)(k + 2) (2k + 3)}{6}}\)
\({1}^{2} + {2}^{2} + {3}^{2} + ..... + {k}^{2} + (k + 1)^{2} = \frac{k (k + 1) (2k + 1) }{6} + \frac{(k + 1) ^{2} }{6} \)
\({1}^{2} + {2}^{2} + {3}^{2} + ..... + {k}^{2} + (k + 1)^{2} = \frac{k(k+1)(2k+1)+6(k+1)^ 2 }{6} \)
\({1}^{2} + {2}^{2} + {3}^{2} + ..... + {k}^{2} + (k + 1)^{2} = \frac{(k+1)\{k(2k+1)+6(k+1)\} }{6}\)
\({1}^{2} + {2}^{2} + {3}^{2} + ..... + {k}^{2} + (k + 1)^{2} = \frac{(k+1)(2k^2 +k+6k+6) }{6} \)
\({1}^{2} + {2}^{2} + {3}^{2} + ..... + {k}^{2} + (k + 1)^{2} = \frac{(k+1)(2k^2+7k+6) }{6} \)
\({1}^{2} + {2}^{2} + {3}^{2} + ..... + {k}^{2} + (k + 1)^{2} = \frac{(k+1)(k+2)(2k+3) }{6} \)
Henceforth, by using the principle of mathematical induction 1²+2² +3²+....+n² = n(n+1)(2n+1)/ 6 for all positive integers n.
_______________________________
Please scroll left - right to view the full solution.
Which statement best describes the function below?
f(x) = 2x3 + 212
1
A. It is not a function,
B. It is a many-to-one function,
0 OOO
C. It fails the vertical line test.
D. It is a one-to-one function!
Answers
Answer:
B
Step-by-step explanation:
Calculate how many weeks, days and hours there are in 4 days 10 hours + 7 days and 16 hours
Answers
Answer:
1 week, 14 days, 24 hours = 1 day,
= 4 days + 7 days + 10 hours + 16 hours
= 11 days + 26 hours
= 11 days 26 hours
Answer:
1 week 5 days 2 hours
Step-by-step explanation:
10 hours + 16 hours = 26hrs = 1 day 2 hours
4 days + 7 days + 1 day 2hrs = 12 days 2 hrs
7 days in a week so 12 days = 1 week 5 days
A computer designer has to build a computer which can executes 300 instructions and represents integers in
\( - {10}^{14} \)
to
\( {10}^{14} \)
lf one instruction is stored in the entire memory word, what is the maximum memory capacity this computer can occupy?
Answers
The computer can occupy a maximum of 1200 bytes of memory.
To determine the maximum memory capacity of a computer that can execute 300 instructions, we need to consider the representation of integers and the storage requirements for instructions.
If each instruction is stored in the entire memory word, it implies that each instruction occupies one memory word. Therefore, the number of instructions executed (300) directly corresponds to the number of memory words required.
The memory capacity of a computer is typically measured in bytes. However, since we are assuming each instruction occupies one memory word, we can consider the memory capacity in terms of memory words.
Hence, the maximum memory capacity this computer can occupy would be 300 memory words.
To convert this capacity into bytes, we need to know the size of a memory word. If we assume the computer uses a 32-bit word size, which is common in many systems, each memory word would consist of 4 bytes (32 bits / 8 bits per byte). Therefore, the maximum memory capacity in bytes would be:
300 memory words * 4 bytes per word = 1200 bytes.
for more such questions on memory
https://brainly.com/question/31399102
#SPJ8
6.The heights of an adult female population are normally distributed
with mean 162 cm and standard deviation 7.5cm.
(a) Find the probability that a randomly chosen adult female is taller
than 150 cm.
(b) Sarah is a young girl. She visits her doctor and is told she is at the
60th percentile for height. Assuming that Sarah remains at the 60th
percentile, estimate her height as an adult. (use table V)

Answers
a) The probability that a randomly chosen adult female is taller than 150 cm, using the normal distribution, is of: 0.9452 = 94.52%.
b) Sarah's adult height will be estimated as: 164 cm.
How to obtain probabilities using the normal distribution?The z-score of a measure X of a variable that has mean symbolized by \(\mu\) and standard deviation symbolized by \(\sigma\) is obtained by the rule presented as follows:
\(Z = \frac{X - \mu}{\sigma}\)
The z-score represents how many standard deviations the measure X is above or below the mean of the distribution, depending if the obtained z-score is positive or negative.Using the z-score table, the p-value associated with the calculated z-score is found, and it represents the percentile of the measure X in the distribution.The mean and the standard deviation of the heights are given as follows:
\(\mu = 162, \sigma = 7.5\)
For item a, the probability that a randomly chosen adult female is taller than 150 cm is one subtracted by the p-value of Z when X = 150, hence:
\(Z = \frac{X - \mu}{\sigma}\)
Z = (150 - 162)/7.5
Z = -1.6
Z = -1.6 has a p-value of 0.0548.
1 - 0.0548 = 0.9452 = 94.52%.
The 60th percentile is X when Z = 0.253, hence:
0.253 = (X - 162)/7.5
X - 162 = 0.253 x 7.5
X = 164 cm.
More can be learned about the normal distribution at https://brainly.com/question/25800303
#SPJ1