Explain whether or not a continuous function can be considered a sequence.
Answers
Answer:
A function is considered continuous when it has no drastic changes in the sequence known as discontinuities. If not continuous, a function is said to be discontinuous.
Related Questions
To rent a van, a moving company charges $30.00 plus $2.50 per mile. The table shows the total cost for the number of miles driven. Enter an equation in slope-intercept form to represent this situation. PLS HELP MEHHHHHH PLS IT'S 100 POINTS
Answers
Answer:
$30.00 to rent the van
.50 per mile x 150 miles
.50*150 = $75.00
30.00 + 75.00 = $105.00
you budgeted 100.00 you do not have enough money
Step-by-step explanation:
I hope that helps i already did this assignment and it was right :)
natasha is in a class of 30 students that selects 4 leaders. how many ways are there to select the 4 leaders so that natasha is one of the leaders? a. (30 4 ) b. (29 4 ) c. (30 3 ) d. (29 3 )
Answers
the correct answer is b. (29 4), which represents the number of ways to select 4 leaders from the remaining 29 students after Natasha is already chosen as one of the leaders.
In this scenario, Natasha is already one of the leaders, so we need to select the remaining 3 leaders from the remaining 29 students. We can use the combination formula (n-1)C(r-1) to calculate the number of ways to choose the leaders.
Using the given options, we can determine the correct choice:
a. (30 4): This option represents selecting 4 leaders from the entire class of 30 students, not accounting for Natasha being one of the leaders.
b. (29 4): This option represents selecting 4 leaders from the remaining 29 students after Natasha is already chosen. This is the correct choice.
c. (30 3): This option represents selecting 3 leaders from the entire class of 30 students, not accounting for Natasha being one of the leaders.
d. (29 3): This option represents selecting 3 leaders from the remaining 29 students after Natasha is already chosen.
Learn more about combination formula here:
https://brainly.com/question/13090387
#SPJ11
A shoemaker sold a pair of for $245.99 if the buyer a $300.00 bill, how much will the buyer receive in change?
*two decimal places don't forget your $ sign. Example: $50.00 NOT 50*
Answers
Answer:
$54.01
Step-by-step explanation:
All you have to do is $300.00-$245.99 .
What’s the mean,median,mode, and range of 5,28,16,32,5,16,48,29,5,35
Answers
Answer:
Step-by-step explanation:
5, 5, 5, 16, 16, 28, 29, 32, 35, 48
Mode: 5, 16
Median: 44/2 = 22
range: 48 - 5 = 43
mean: (5 + 5 + 5 + 16 + 16 + 28 + 29 +32 + 35 + 48)/10 = 219/10 = 21.9
Please helppppppppppppppppppppppppppppppppppppppp

Answers
Answer:
Step-by-step explanation:
please help ! ASAP step by step explanation please

Answers
Answer:
0
Step-by-step explanation:
→ First find inverse cosine 1/2
60°
→ Now multiply this answer by 3 because then if you substitute it in you get 0.5
∝ = 180°
→ Now find sine of 180°
0
a sheet of gold weighing 10.0 g and at a temperature of 18.0°c is placed fl at on a sheet of iron weighing 20.0 g and at a temperature of 55.6°c. what is the fi nal temperature of the combined metals?
Answers
When different metals with different temperatures are placed together, they tend to exchange heat until the temperature becomes equal. This phenomenon is known as Thermal Equilibrium.
The final temperature of the combined metals can be calculated using the following formula:
Q = m * c * ∆T
Where,Q = Heat exchanged by metals m = Mass of metals c = Specific Heat of metal∆T = Change in temperature
Assuming no heat is lost to the surroundings, we can say that the Heat lost by the hot iron is equal to the Heat gained by the cold gold.
Hence, m1 * c1 * ∆T1 = m2 * c2 * ∆T2.
Rearranging the equation,
we get ∆T = (m1 * c1 * ∆T1) / (m2 * c2).
Now substituting the values, we get;For gold, m = 10 g, c = 0.129 J/g°C, ∆T = (Tfinal - 18°C).
For iron, m = 20 g, c = 0.449 J/g°C, ∆T = (55.6 - Tfinal).
We get ∆T = (10 * 0.129 * (Tfinal - 18)) / (20 * 0.449) = (1.29 * (Tfinal - 18)) / 8.98.
Now equating the two, we get (Tfinal - 18) / 8.98 = (55.6 - Tfinal) / 20.
Solving the equation,
we get Tfinal = (55.6 * 8.98 + 18 * 20) / (8.98 + 20) = 30.18°C.
Hence the final temperature of the combined metals is 30.18°C.
To know more about Thermal Equilibrium visit:
https://brainly.com/question/14473445
#SPJ11
Foster picked 50 figs and divided them into 5 baskets. If each fig was $3, how much is one basket?
Answers
Answer:
$30
Step-by-step explanation:
50÷5=10x3=30
answerrrr plzzzzzzzzzzzzz
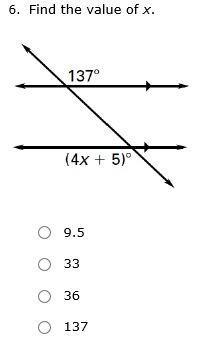
Answers
Answer:
33 big man
Step-by-step explanation:
i need brainliest plzz
Answer: 33
Explanation:
1) Subtract 5 from both sides of the equation
4+5=137
4x+5=137
4x+5=137
4+5−5=137−5
2)Simply
Subtract the numbers
Divide by 4
4=132
Cancel terms that are in both the numerator and denominator
Divide the numbers
=33
Solution
=33
need help asap ill give 100 points simplify the radicals

Answers
Answer:
8d\(\sqrt{e}\)
Step-by-step explanation:
using the rule of radicals
\(\sqrt{ab}\) = \(\sqrt{a}\) × \(\sqrt{b}\)
given
\(\sqrt{25d^2e}\) - \(\sqrt{d^2e}\) + 2\(\sqrt{4d^2e}\)
evaluating each term separately
\(\sqrt{25d^2e}\)
= \(\sqrt{25}\) × \(\sqrt{d^2}\) × \(\sqrt{e}\)
= 5 × d × \(\sqrt{e}\)
= 5d\(\sqrt{e}\)
-------------------
\(\sqrt{d^2e}\)
= \(\sqrt{d^2}\) × \(\sqrt{e}\)
= d × \(\sqrt{e}\)
= d\(\sqrt{e}\)
-------------------
\(\sqrt{4d^2e}\)
= \(\sqrt{4}\) × \(\sqrt{d^2}\) × \(\sqrt{e}\)
= 2 × d × \(\sqrt{e}\)
= 2d\(\sqrt{e}\)
-----------------------
then combining them gives
5d\(\sqrt{e}\) - d\(\sqrt{e}\) + 2(2d\(\sqrt{e}\))
= 4d\(\sqrt{e}\) + 4d\(\sqrt{e}\)
= 8d\(\sqrt{e}\)
Consider simple planer . 4-reguler graph with 6 verticles 4-regular means chat all verticles have degree 4. How many edges? how many regions ? Draw all verticies have degree Such a gr
Answers
A simple planar graph, 4-regular with 6 vertices will have 12 edges and 8 regions. Each vertex has a degree of 4, meaning it is connected to exactly 4 edges
To draw such a graph, we can start by placing the 6 vertices in a circular arrangement.
Each vertex will be connected to the 4 adjacent vertices, ensuring that the graph is 4-regular. By connecting the vertices accordingly, we will obtain a graph with 12 edges and 8 regions.
The regions are the bounded areas created by the edges of the graph when drawn on a plane.
To know more about planar graph refer here:
https://brainly.com/question/31771828#
#SPJ11.
The length of a rectangle is 1 7/9 in and its width is 3/4 of its length. Find the area of this rectangle.
Answers
Answer:
The answer is 4/3 or 1.33 square units.
Step-by-step explanation:
Length = 1 + 7/9 = 16/9 units.
Width = 3/4 units.
Since area of rectangle = Length * Width
Area = 16/9 * 3/4 = 4/3 square units.
Find the area of the shape below

Answers
Answer:
32 units^2
Step-by-step explanation:
This is a trapezoid
The area of a trapezoid is found by
A = 1/2 (b1+b2) h
A = 1/2 ( 4+12) *4
A = 1/2 (16) *4
A =32
Answer:
I think the answer is 32.!
Step-by-step explanation:
Anyone please correct me if I'm wrong.
I would divide the 12 into 3 to get 4 for the 3 parts.
I will start with the triangle on the left 4 times 4=16. Divide it 1/2, which you get 8.
On the triangle on the right is the same, so 8.
The middle is 4 times 4=16.
Last 8+8+16=32.
I think the answer is 32 units.!
find the horizontal and vertical asymptotes of the curve. y = 3ex ex − 5
Answers
The graph of y = 3ex ex − 5 has a horizontal asymptote of y = 3 and a vertical asymptote of x = -3/5.
The equation y = 3ex ex − 5 can be rewritten as y = 3x2ex − 5. In order to find the horizontal and vertical asymptotes of this function, we must first find its degree of the numerator and denominator. The numerator is a second degree polynomial while the denominator is a first degree polynomial.
The horizontal asymptote will be the line y = b/a, where b and a are the coefficients of the highest degree terms in the numerator and denominator, respectively. In this case, b = 3 and a = 1, so the horizontal asymptote is y = 3.
The vertical asymptote of a function is the line x = a/b, where a and b are the coefficients of the highest degree terms in the numerator and denominator, respectively. In this case, a = 3 and b = -5, so the vertical asymptote is x = -3/5.
Therefore, the graph of y = 3ex ex − 5 has a horizontal asymptote of y = 3 and a vertical asymptote of x = -3/5.
Learn more about vertical asymptote here:
https://brainly.com/question/12191454
#SPJ4
Solve for m
-8m-=7-9m
M=?
Answers
Answer:
\(\boxed{m = 7}\)
Step-by-step explanation:
Hey there!
Well to solve for m in the given equation,
-8m = -7 - 9m
Single out m
+ 9 to both sides
m = 7
Hope this helps :)
Answer:
m = 7
Step-by-step explanation:
-8m+9m=7-9m
Add 9m to each side
-8m+9m=7-9m
m = 7
If vertical angles are congruent, then two lines cut by a transversal are parallel.
a. True
b. False
Answers
The answer is True. If two vertical angles are congruent, then two lines cut by a transversal will be parallel.
Vertical angles are angles that are opposite each other and share the same vertex. They are congruent angles, meaning that they have the same measure. When two angles are congruent, the sides of the angles are parallel. This means that the two lines cut by a transversal will also be parallel.
The formula for this is that if two angles are congruent, then the lines cut by a transversal are parallel. This is also known as the Angle-Angle-Angle (AAA) Postulate. This postulate states that if two angles of one triangle are congruent to two angles of another triangle, then the two triangles are similar. This means that the lines cut by a transversal are parallel.
In other words, if two angles of a triangle are congruent, then the two sides of the triangle that make those angles are parallel. This is because the two angles are congruent, meaning that they have the same measure. Therefore, if two vertical angles are congruent, then two lines cut by a transversal will be parallel.
Learn more about Vertical angles here :
https://brainly.com/question/24460838
#SPJ4
You have a deck of cards. You pull 2 cards. What is the probability of pulling a red
card or a king with replacement.
a. 15/26
b. 0
c. 7/13
Answers
Answer:
7/13
Step-by-step explanation:
i just took the quiz
The center of a normal curve is a. cannot be negative b. always equal to zero c. is the mean of the distribution d. is the standard deviation
Answers
The center of a normal curve is the mean of the distribution, making option C the right choice.
A normal distribution—also known as the bell curve or De Moivre distribution—occurs naturally in a variety of circumstances. Bell curve symmetry is present. The data will split in two, falling half to the left and half to the right of the mean.
The characteristics of a normal curve are as follows:
Bell-like symmetrical form.The distribution's mean and median, both of which are situated in their center, are equal. ≈ 68% of the data is within one standard deviation of the mean. ≈ 95% of the data is within two standard deviations of the mean. ≈ 99.7% of the data is within three standard deviations of the mean.Thus, the center of a normal curve is the mean of the distribution, making option C the right choice.
Learn more about normal curves at
https://brainly.com/question/23418254
#SPJ4
If the diameter of the ball is 11 cm, what is the distance from the center of the ball to where the board meets the floor to the nearest tenth of a centimeter
Answers
The distance from the centre of the ball to where the ball meets the floor is 5.5 cm.
How to find the diameter of the ball?The diameter of the ball is 11 centimetres, Therefore, the distance from the centre of the ball to where the ball meets the floor to the nearest tenth of a centimetres can be calculated as follows:
Therefore, the distance form the centre of the ball to the floor is the radius of the floor.
Hence,
distance from the centre of the ball to where the ball meets the floor = 11 / 2
distance from the centre of the ball to where the ball meets the floor = 5.5 cm
learn more on diameter here: https://brainly.com/question/10012417
#SPJ1
Historically, the members of the chess club have had an average height of 5′6 ′′ with a standard deviation of 2 ′′. What is the probability of a player being between 5′3 ′′ and 5' 10"? (Submit your answer as a whole number. For example if you calculate 0.653 (or 65.3% ), enter 65. )
Answers
The probability of a player being between 5′3 ′′ and 5' 10" is 77%.
To calculate the probability of a player being between 5′3 ′′ and 5' 10", we need to standardize the values using the formula:
z = (x - μ) / σ
where x is the height of the player, μ is the mean height of the chess club members, and σ is the standard deviation of the heights.
For x = 5′3 ′′, z = (63 - 66) / 2 = -1.5
For x = 5'10", z = (70 - 66) / 2 = 2
Using a standard normal distribution table or calculator, we can find the area under the curve between z = -1.5 and z = 2, which represents the probability of a player being between 5′3 ′′ and 5' 10".
This area is approximately 0.7745 or 77%.
Therefore, the value obtained is 77%.
To know more about probability refer here:
https://brainly.com/question/11034287#
#SPJ11
For a family with 3 children, what is the probability that they have exactly 2 boys and 1 girl?
Answers
Answer:
\(\frac{3}{8}\)
Step-by-step explanation:
Possibilities (G for girls and B for boys):
GGG
GGB
GBG
GBB
BGG
BGB
BBG
BBB
Answer:
1/4
Step-by-step explanation:
There are a total of four possibilities,
- Three girls
- Three boys
- Two girls and One boy
- Two boys and One girl
and only one of those options are 2 boys and 1 girl
The outside temperature is -13 degrees. The temperature drops by 9 degrees, but then increases by 16 degrees. What is the final temperature outside? *
Answers
Answer:
The final outside temperature = -6°
Step-by-step explanation:
GIven that :
the outside temperature = -13°
The temperature drops by 9°
But then increases by 16°.
The final temperature can be expressed as:
the outside temperature - temperature drop
= -( 13° - 9°)
= - 22°
it is said that the temperature later increase by 16°
∴ - 22° + 16°
= -6°
The final outside temperature = -6°
determine the surface area of a box whose length l is 21 feet, width w is 6 feet, and height h is 8.5 feet.
Answers
To determine the surface area of the box, we need to find the area of each of its six sides and add them together. Let's start with the top and bottom of the box, which are both rectangles with length l and width w. The area of one of these rectangles is: l x w = 21 ft x 6 ft = 126 sq ft
Since there are two of these rectangles (top and bottom), we need to multiply this by 2 to get the total area of both:
2 x 126 sq ft = 252 sq ft
Next, let's look at the four vertical sides of the box, which are also rectangles. Each one has a height of h and a width of either l or w. The area of one of these rectangles is:
h x l = 8.5 ft x 21 ft = 178.5 sq ft
Again, there are two of these rectangles (front and back) with area 178.5 sq ft each, and two more (left and right) with area w x h = 6 ft x 8.5 ft = 51 sq ft each. So the total area of all four vertical sides is:
2 x 178.5 sq ft + 2 x 51 sq ft = 409 sq ft
Finally, we can add up the areas of all six sides to get the total surface area of the box:
252 sq ft + 409 sq ft = 661 sq ft
Therefore, the surface area of the box is 661 square feet.
To know more about surface area visit:
https://brainly.com/question/27963638
#SPJ11
PLEASE ANSWER THE FOLLOWING QUESTION GIVEN THE CHOICES!!!

Answers
Answer: 3/52
Step-by-step explanation:
You want to pick a diamond jack, diamond queen or diamond king
There are only 3 of those so
P(DJ or DQ or DK) = 3/52 There are 3 of those out of 52 total
Evaluate cos(780°) using the unit circle
Answers
The value of cos 780 using the unit circle is 0.5
Angle in a circleGiven the following angle
cos780To get the equivalent angle, we will need to write the angle to fall between the angles in a circle
cos 780 = cos(780 - 720)
cos 780 = cos 60
cos 780 = 0.5
Hence the value of cos 780 using the unit circle is 0.5
Learn more on unit circle here: https://brainly.com/question/23989157
One-third of the students in Mrs. Hayko's class walk to school. Of the students who do not walk to school, four-fifths take the bus.
a.) What fraction of the students in Mrs. Hayko's class take the bus to school?
b.) How many students might be there in her class?
Answers
Answer:
The possible number of students in Mrs. Hayko's class is limited to 15 or 30, as higher multiples of 15 would exceed the desired class size.
Step-by-step explanation:
a)
Let 'x' be the total number of students in Mrs. Hayko's class.
One-third of the students walk to school: (1/3)x.
The remaining students who do not walk to school: (2/3)x.
Four-fifths of the non-walking students take the bus: (4/5) * (2/3)x.
Simplify to find the fraction of students taking the bus: (8/15)x.
b)
Consider different values for 'x' to find a whole number of students taking the bus.
Start with a small number, such as x = 15.
Calculate the number of students taking the bus using (8/15)x.
If the result is a whole number, it's a possible class size.
Repeat with different values of 'x' until a whole number is obtained.
The possible number of students in Mrs. Hayko's class could be 15, 30, or any other multiple of 15.
teo has a combination of quarters loonies and toonies in his pocket .He knows he has 9 coins in total and that he has atleastone of each type of coin.
a) what is the probability that teo has more than $8
b) How many different combinations of coins could teo useto pay for an item that costs between $10 and $12, if he uses fewer toonies than loonies
Answers
a) The probability is 1 out of the total number of combinations.
b) Each case would involve finding the possible combinations of quarters that would result in a total value between $10 and $12.
a) To determine the probability that Teo has more than $8, we need to consider the possible combinations of quarters, loonies, and toonies that would result in a total value greater than $8. Since Teo has 9 coins in total, we can analyze the different scenarios:
Case 1: Teo has 1 toonie, 1 loonie, and 7 quarters. The total value would be $2 + $1 + (7 * $0.25) = $2 + $1 + $1.75 = $4.75, which is less than $8.
Case 2: Teo has 2 toonies, 1 loonie, and 6 quarters. The total value would be $4 + $1 + (6 * $0.25) = $4 + $1 + $1.50 = $6.50, which is less than $8.
Case 3: Teo has 3 toonies, 1 loonie, and 5 quarters. The total value would be $6 + $1 + (5 * $0.25) = $6 + $1 + $1.25 = $8.25, which is greater than $8.
Therefore, there is only one possible combination out of the total combinations where Teo has more than $8.
b) To determine the number of different combinations of coins that Teo could use to pay for an item between $10 and $12, considering fewer toonies than loonies, we can analyze the possible scenarios:
Case 1: Teo has 0 toonies, 1 loonie, and a combination of quarters. The value of 1 loonie is $1. Teo needs to have additional coins totaling between $9 and $11, which can be achieved using different combinations of quarters.
Case 2: Teo has 1 toonie, 1 loonie, and a combination of quarters. The value of 1 toonie and 1 loonie is $3. Teo needs to have additional coins totaling between $7 and $9, which can be achieved using different combinations of quarters.
We can continue analyzing different cases where Teo has more toonies and/or more loonies.
Determining the exact number of different combinations of coins would involve listing and calculating each scenario, which can be time-consuming. Therefore, it would be more practical to use a systematic approach, such as generating combinations using mathematical or programming methods, to calculate the total number of different combinations of coins that meet the given criteria.
for more such questions on probability
https://brainly.com/question/25839839
#SPJ8
What percent of 70 is 84?
% of 70 is 84.
Answers
Answer:
120
Step-by-step explanation:
Just did this
Answer:
ig 174
Step-by-step explanation:
A bag of popcorn is placed in a microwave. After the first kernel pops, the number of kernels popped doubles every 30 seconds. If it takes exactly two minutes for every kernel in the bag to have popped, what would the time be on the microwave when 25% of the kernels have popped?
Answers
Let there be N number of kernels in the bag.
Given that the number o
D²y(t) + 12 Dy(t) + 36y(t) = 2 e-5t y(0) = 1, Dy(0)=0 Solve the differemtial equation using Classical Method (30pts) and Laplace Transform Method(30pts)
Answers
The solution to the differential equation D²y(t) + 12 Dy(t) + 36y(t) = 2 \(e^{(-5t)}\), with initial conditions y(0) = 1 and Dy(0) = 0, is \(y(t) = (1 + 6t) e^{(-6t)}\).
To solve the given differential equation using the classical method, we can assume a solution of the form \(y(t) = e^{(rt)}\) and find the values of r that satisfy the equation. We then use these values of r to construct the general solution.
Using the classical method:
Substitute the assumed solution \(y(t) = e^{(rt)}\) into the differential equation:
D²y(t) + 12 Dy(t) + 36y(t) = \(2 e^{(-5t)}\)
This gives the characteristic equation r² + 12r + 36 = 0.
Solve the characteristic equation for r by factoring or using the quadratic formula:
r² + 12r + 36 = (r + 6)(r + 6)
= 0
The repeated root is r = -6.
Since we have a repeated root, the general solution is y(t) = (c₁ + c₂t) \(e^{(-6t)}\)
Taking the first derivative, we get Dy(t) = c₂ \(e^{(-6t)}\)- 6(c₁ + c₂t) e^(-6t).\(e^{(-6t)}\)
Using the initial conditions y(0) = 1 and Dy(0) = 0, we can solve for c₁ and c₂:
y(0) = c₁ = 1
Dy(0) = c₂ - 6c₁ = 0
c₂ - 6(1) = 0
c₂ = 6
The particular solution is y(t) = (1 + 6t) e^(-6t).
Using the Laplace transform method:
Take the Laplace transform of both sides of the differential equation:
L{D²y(t)} + 12L{Dy(t)} + 36L{y(t)} = 2L{e^(-5t)}
s²Y(s) - sy(0) - Dy(0) + 12sY(s) - y(0) + 36Y(s) = 2/(s + 5)
Substitute the initial conditions y(0) = 1 and Dy(0) = 0:
s²Y(s) - s - 0 + 12sY(s) - 1 + 36Y(s) = 2/(s + 5)
Rearrange the equation and solve for Y(s):
(s² + 12s + 36)Y(s) = s + 1 + 2/(s + 5)
Y(s) = (s + 1 + 2/(s + 5))/(s² + 12s + 36)
Perform partial fraction decomposition on Y(s) and find the inverse Laplace transform to obtain y(t):
\(y(t) = L^{(-1)}{Y(s)}\)
Simplifying further, the solution is:
\(y(t) = (1 + 6t) e^{(-6t)\)
To know more about differential equation,
https://brainly.com/question/32622859
#SPJ11