Expand 1998 x 2002 without a calculator
Answers
Answer:
3,999,996.
Step-by-step explanation:
We can use the distributive property of multiplication to expand 1998 x 2002 as follows:
1998 x 2002 = (2000 - 2) x (2000 + 2)
Using the FOIL method, we can expand the product of these two binomials:
(2000 - 2) x (2000 + 2) = 2000 x 2000 + 2 x 2000 - 2 x 2000 - 2 x 2
Simplifying the terms, we get:
2000 x 2000 - 4 = 3,999,996
Therefore, 1998 x 2002 is equal to 3,999,996.
Related Questions
The weights of adult male rhesus monkeys are normally distributed, with a mean of 15 pounds and a standard deviation of 3 pounds.
1. The probability that a randomly chosen rhesus monkey weighs between 10 pounds and 13 pounds is closest to
a) 0.7961 b) 0.2514 c) 0.2047 d) 0.0475 e) 1.2334
2. If 50 rhesus monkeys are randomly selected, then approximately how many are expected to weigh less than 12 pounds?
a) 5 b) 25 c) 30 d) 8 e) 23
3. To be in the top 13% of the weights, a rhesus monkey should weigh at least
a) 18.38 pounds b) 25.27 pounds c) 17.52 pounds d) 15 pounds e) 20.64 pounds
Answers
1. The probability that a randomly chosen rhesus monkey weighs between 10 pounds and 13 pounds is closest to (C) 0.2047. 2. If 50 rhesus monkeys are randomly selected, then approximately (D) 8 are expected to weigh less than 12 pounds. 3. To be in the top 13% of the weights, a rhesus monkey should weigh at least (A) 18.38 pounds.
The Explanation to Question 1The probability that a randomly chosen rhesus monkey weighs between 10 pounds and 13 pounds can be calculated using the Z-score formula:
Z = (X - μ) / σWhere X is the value we are interested in, μ is the mean, and σ is the standard deviation.
For 10 pounds: Z = (10 - 15) / 3 = -1.67
For 13 pounds: Z = (13 - 15) / 3 = -0.67
Using the standard normal table, we can find the probability for these Z-scores:
P(Z < -1.67) = 0.0475P(Z < -0.67) = 0.2514
The probability that a randomly chosen rhesus monkey weighs between 10 pounds and 13 pounds is the difference between these two probabilities:
Therefore, the closest answer is c) 0.2047.
If 50 rhesus monkeys are randomly selected, then we can use the same Z-score formula to find the probability that a monkey weighs less than 12 pounds:
Z = (12 - 15) / 3 = -1P(Z < -1) = 0.1587The expected number of monkeys that weigh less than 12 pounds is the product of the probability and the sample size:
E = 0.1587 * 50 = 7.935Therefore, the closest answer is d) 8.
The Explanation to Question 3
To be in the top 13% of the weights, a rhesus monkey should have a Z-score that corresponds to the 87th percentile (100 - 13 = 87). Using the standard normal table, we can find the Z-score that corresponds to the 87th percentile:
P(Z < 1.13) = 0.8708Using the Z-score formula, we can solve for X:
1.13 = (X - 15) / 3X = 18.39Therefore, the closest answer is a) 18.38 pounds.
Learn more about probability of randomly chosen https://brainly.com/question/30359938
#SPJ11
Keisha buys 2 pens at the store. Each pen costs $2. Which graph shows the coordinates of the point that represents the number of pens that Keisha buys and the total cost? PLES IM DOING A TEST RN
Answers
The coordinate of the point that represents the number of pens that Keisha buys and the total cost is (2, 4)
How to determine the graph shows the coordinates of the point that represents the number of pens that Keisha buys and the total cost?The given parameters are
Number of pen = 2
Unit price = $2
This means that the total amount spent is
Total amount = Number of pen * Unit price
Evaluate the product
Total amount = 2 * 2
Evaluate the product
Total amount = 4
So, the coordinate of the point that represents the number of pens that Keisha buys and the total cost is (2, 4)
Read more about coordinate at:
https://brainly.com/question/17206319
#SPJ1
On Monday, Jake could lift 25 lbs. One
year later, the weight he could lift
increased by 30%. What is the number
of pounds he can lift a year later?
Answers
complete the missing value in the solutuion to the equation

Answers
Answer:
Step-by-step explanation:
5x-2y=30
Given x=8
5×8-2y=30
-2y=30-40
y=5
Use K-maps to minimize these sum-of-products expansions F(z,y,z)=xyz+xy
′
z
′
+x
′
yz
′
+x
′
y
′
z
′
Answers
The minimized sum-of-products expression is x'z' + y'z'.
To minimize the sum-of-products expression F(z, y, z) = xyz + xy'z' + x'y'z' + x'y'z, we can use Karnaugh maps (K-maps). K-maps provide a visual method for simplifying Boolean expressions.
Step 1: Construct the K-map
We create a K-map for the three variables z, y, and x. Each variable will have two rows and two columns since there are two possible values for each variable (0 and 1). Label the rows and columns with the binary representations of the variables.
yz\ x | 00 | 01 | 11 | 10 |
-----------------------------
00 | | | | |
-----------------------------
01 | | | | |
-----------------------------
11 | | | | |
-----------------------------
10 | | | | |
Step 2: Fill in the K-map
For each minterm in the sum-of-products expression, mark the corresponding cell in the K-map with a 1. The minterms in the expression are xyz, xy'z', x'y'z', and x'y'z.
yz\ x | 00 | 01 | 11 | 10 |
-----------------------------
00 | | 1 | | 1 |
-----------------------------
01 | 1 | | | |
-----------------------------
11 | | | | |
-----------------------------
10 | | | | |
Step 3: Group adjacent 1's in the K-map
Look for adjacent 1's in the K-map and group them in the largest power-of-2 rectangles possible. Each group should contain a number of 1's that is a power of 2 (1, 2, 4, 8, etc.).
yz\ x | 00 | 01 | 11 | 10 |
-----------------------------
00 | | 1 | | 1 |
-----------------------------
01 | 1 | | | |
-----------------------------
11 | | | | |
-----------------------------
10 | | | | |
In this case, we have two groups: one with two adjacent 1's and another with one 1.
Step 4: Determine the simplified expression
For each group, identify the common variables and their values (0 or 1). Write down the simplified expression based on these variables.
Group 1: x'z'
Group 2: y'z'
Combine the expressions for each group using the OR operator (+) to get the final simplified expression:
F(z, y, z) = x'z' + y'z'
So the minimized sum-of-products expression for F(z, y, z) is x'z' + y'z'.
To learn more about expression here:
https://brainly.com/question/28170201
#SPJ4
In a complete paragraph, pick a scenario where concepts from this algebra course would be used - it could be in your own life, it could be in a specific work field such as a construction worker, or working in a business, etc. Choose at least 2-3 concepts to include, explain your scenario, how these concepts apply, and provide a worked example for each concept. Use the following format: Topic Sentence: 1 concise sentence describing a scenario where concepts from this course could be used. Supporting Detail: 1-2 sentences explaining how 1 concept from the class can be applied to the scenario. Worked Example: Show a worked example for the concept described above. Supporting Detail: 1-2 sentences explaining how 1 concept from the class can be applied to the scenario. Worked Example: Show a worked example for the concept described above. Conclusion: 1-2 sentences describing how applying the concepts in this algebra course to a real-life situation helps in understanding the material in the course.
Answers
Scenario: A small business owner needs to analyze their sales data to make informed decisions about pricing and profitability.
Supporting Detail 1: The concept of linear equations can be applied to determine the break-even point and set optimal pricing strategies for the business.
Worked Example 1: Let's say the small business sells a product for $10 each, and the fixed costs (expenses that don't vary with the number of units sold) amount to $500. The variable costs (expenses that depend on the number of units sold) are $2 per unit. We can use the formula for a linear cost equation (C = mx + b) to find the break-even point where revenue equals total costs:
10x = 2x + 500
Simplifying the equation, we get:
8x = 500
x = 500/8
x = 62.5
The break-even point is 62.5 units. Knowing this information, the business owner can make decisions about pricing, cost control, and production targets.
Supporting Detail 2: The concept of systems of equations can be applied to optimize the allocation of resources in the business.
Worked Example 2: Let's consider a scenario where the business owner sells two different products. Product A generates a profit of $5 per unit, while Product B generates a profit of $8 per unit. The business owner has a limited budget of $500 and wants to determine the optimal allocation of resources between the two products. We can set up a system of equations to represent the profit constraints:
x + y = 500 (total budget)
5x + 8y = P (total profit, represented as P)
By solving this system of equations, the business owner can find the optimal values of x and y that maximize the total profit while staying within the budget constraints.
Conclusion: Applying concepts from this algebra course to real-life scenarios, such as analyzing sales data for a small business, helps in understanding the material by providing practical applications. It demonstrates the relevance of algebra in making informed decisions, optimizing resources, and maximizing profitability.
These examples highlight how algebraic concepts enable problem-solving and provide valuable tools for individuals in various fields, including business and entrepreneurship.
For more such questions on profitability
https://brainly.com/question/29982132
#SPJ8
Someone’s pls give me the answer to this!

Answers
Answer:
3/10
Step-by-step explanation:
(2/5)*2=4/10. 7/10-4/10=3/10
Answer:
3/10
Step-by-step explanation:
2/5 + x = 7/10
Get a common denominator of 10
2/5 * 2/2 = 4/10
4/10 +x = 7/10
Subtract 4/10 from each side
4/10 +x -4/10 = 7/10 -4/10
x = 3/10
The following confidence interval is obtained for a population proportion, p: (.688, .724). Use these confidence interval limits to find the point estimate, p.
A. .688
B. .724
C. .706
D. 708
Answers
The point estimate, p, based on the given confidence interval (.688, .724), is .706.
To find the point estimate, p, we take the midpoint of the confidence interval.
In this case, the lower limit is .688 and the upper limit is .724.
To find the midpoint, we calculate the average of these two values.
Midpoint = (lower limit + upper limit) / 2
= (.688 + .724) / 2
= 1.412 / 2
= .706
Therefore, the point estimate, p, is .706.
The point estimate represents our best estimate for the true population proportion based on the available sample data.
In this case, it suggests that the proportion, p, is most likely around .706.
However, it's important to note that the point estimate is subject to sampling variability and may not perfectly reflect the true population proportion.
706 is the correct answer as it represents the point estimate obtained from the confidence interval limits provided.
Learn more about Sample Data from the given link :
https://brainly.com/question/33527107
#SPJ11
simplify these expressions. a) x ⊕ 0 b) x ⊕ 1 c) x ⊕ x d) x ⊕ x
Answers
a) x b) 1 c) 0 d) x , x ⊕ x ⊕ 0 → Since 0 is the neutral element of the XOR operator, it will not affect the result of the expression. Therefore, the expression simplifies to just x.
a) x ⊕ 0 → Since 0 is the neutral element of the XOR operator, it will not affect the value of x. Therefore, the expression simplifies to just x.
b) x ⊕ 1 → Since 1 is the identity element of the XOR operator, it will return the opposite of x. Therefore, the expression simplifies to just 1.
c) x ⊕ x → Since x ⊕ x is equivalent to x XORing itself, the result will be 0. Therefore, the expression simplifies to just 0.
d) x ⊕ x ⊕ 0 → Since 0 is the neutral element of the XOR operator, it will not affect the result of the expression. Therefore, the expression simplifies to just x.
a) x ⊕ 0 simplifies to just x.
b) x ⊕ 1 simplifies to just 1.
c) x ⊕ x simplifies to just 0.
d) x ⊕ x ⊕ 0 simplifies to just x.
Learn more about expression here
https://brainly.com/question/14083225
#SPJ4
There are 120 calories in a 3/4 cup serving of cereal how many calories are there in 6 cups of cereal
Answers
Answer:
960 I believe.
Step-by-step explanation:
let the random variables and have the joint pmf find the means and , the variances and , the covariance , and the correlation coefficient . are and independent or dependent?
Answers
To find the means, variances, covariance, and correlation coefficient of random variables X and Y with a joint PMF:
- Calculate the means: E[X] and E[Y].
- Compute the variances: Var(X) and Var(Y).
- Find the covariance: Cov(X, Y).
- Determine the correlation coefficient: ρ(X, Y).
Based on the covariance, we can determine if X and Y are independent or dependent.
Let the random variables X and Y have a joint probability mass function (PMF). We need to find the means (expected values), variances, covariance, and correlation coefficient of X and Y, and determine whether they are independent or dependent.
The mean of a random variable X is denoted by E[X] or μX, and it is calculated as the sum of all possible values of X weighted by their respective probabilities. Similarly, the variance of X, denoted by Var(X) or σ²X, measures the spread or dispersion of the values of X around its mean.
The covariance between two random variables X and Y, denoted by Cov(X, Y), measures the degree to which they vary together. It is calculated as the sum of the products of the differences of the values of X and its mean, and the differences of the values of Y and its mean, weighted by their joint probabilities.
The correlation coefficient between X and Y, denoted by ρ(X, Y), quantifies the strength and direction of the linear relationship between them. It is calculated by dividing the covariance of X and Y by the product of their standard deviations.
To determine the means and variances, we can use the following formulas:
E[X] = ∑x∑y x * P(X = x, Y = y)
E[Y] = ∑x∑y y * P(X = x, Y = y)
Var(X) = E[X²] - (E[X])²
Var(Y) = E[Y²] - (E[Y])²
To calculate the covariance, we use the formula:
Cov(X, Y) = E[XY] - E[X]E[Y]
Once we have the means and variances, we can calculate the correlation coefficient using the formula:
ρ(X, Y) = Cov(X, Y) / (√Var(X) * √Var(Y))
Based on the calculations of means, variances, covariance, and correlation coefficient, we can determine whether X and Y are independent or dependent. If the covariance is zero (Cov(X, Y) = 0), then X and Y are independent. Otherwise, they are dependent.
In summary, to find the means, variances, covariance, and correlation coefficient of X and Y, we use the formulas mentioned above. Based on the calculated values, we can determine whether X and Y are independent or dependent.
To know more about joint probability mass function, refer here:
https://brainly.com/question/32066487#
#SPJ11
What happens to the value of the expression as 50/p decreases from a large positive number to a small positive number?
Answers
Answer:
50/p increases from a small positive number to a big positive number.
Step-by-step explanation:
p is in the denominator. This means that p and the value of the expression 50/p are inverse proportional. So for a big value of p, 50/p has a small positive value. For a small value of p, 50/p has a high positive value.
what happens to the value of the expression 50/p as p decreases from a large positive number to a small positive number?
50/p increases from a small positive number to a big positive number.
For example
50/1000 = 0.05
50/1 = 50
MATH HELP! BRAINLIESTT!!
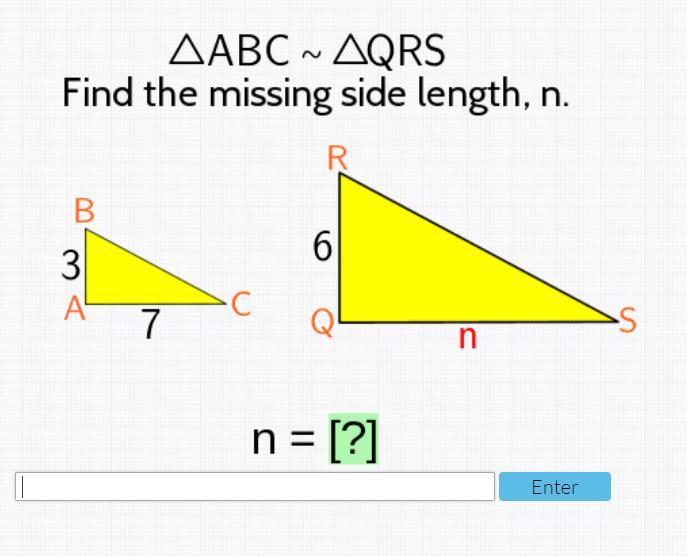
Answers
Answer:
14
Hope it helps.......⋋✿ ⁰ o ⁰ ✿⋌
Answer:
n = 14
Step-by-step explanation:
ΔABC was dilated by a scale factor of 2.
Simplify the expression:
-29 - 1 - 4 - 89
Answers
Answer:
-123
Step-by-step explanation:
Answer:
-123
Step-by-step explanation:
-(29+1+4+89)
-(30+4+89)
-(34+89)
-123
hope this helps good luck at school :))
dr. hellsing has designed a test to measure the level of scientific knowledge in high school graduates. to establish a norm against which individual scores may be interpreted and compared, dr. hellsing is currently administering the test to a large representative sample of high school graduates. dr. hellsing is in the process of:
Answers
She is now giving the test to a sizable representative sample of high school graduates in order to establish a norm against which individual scores may be evaluated and compared. Finding the test's aptitude is what Dr. Hellsing is doing right now.
What is meant by test's aptitude?A test known as an aptitude test is used to assess a person's aptitude for a certain activity. Aptitude tests create the assumption that each person contains their own unique set of strengths and limitations as well as a predisposition to succeed or fail in a given situation based on their innate traits.
A notable illustration of a multiple aptitude test is the Scholastic Assessment Test (SAT) that high school seniors take.
An aptitude test is a type of psychometric evaluation that measures a person's innate talents in a specific field. It is distinct from a knowledge-based test in that it doesn't demand expertise with a certain subject. Instead, it examines your natural talents and your capacity to use them in novel circumstances.
To learn more about test's aptitude refer to:
https://brainly.com/question/28000265
#SPJ1
Simplify the following
a)
\( \frac{5}{8} - \frac{1}{4} + 1 \ \frac{1}{2} \)
b)
\(1 \ \frac{2}{3} + \frac{1}{2} - \frac{1}{6} \)
c)
\(1 + \frac{1}{2} - \frac{1}{3} \)
Answers
a) 15/8
b) 2
c) 7/6
(Just pop them into a calculator)
B. 2
C. 7/6
Hope this helped!
All you have to do is use a calculator! :)
Would appreciate brainliest!
Mr. Rojas spent d dollars to go on vacation. He bought a plane ticket for $250 and stayed in a hotel for 5 nights. If the cost of the hotel room was the same each night, what expression can be used to find how much Mr. Rojas paid each night for the hotel?
Answers
Answer:
x = d/5 - $50
Step-by-step explanation:
Basiclly what this sentence is saying that the price d is equal to $250 + 5 prices of staying in a hotel for a night.
If we let "x" be the price per night then we can get the following..
d = $250 + 5x
5x = d - $250
\(x = \frac{d - 250}{5}\)
x = d/5 - $50
What does a hexagon look like in math?
Answers
A closed, two-dimensional, six-sided polygon in geometry is called a hexagon.
A closed, two-dimensional, six-sided polygon in geometry is called a hexagon. It has six vertices, which together create six internal angles and six line segments. The total of a hexagon's internal angles is 720°. A hexagon's form is also shown in the illustration below:
Based on the dimensions of the sides and angles, we can divide the hexagonal form into numerous categories. With the help of pertinent figures and examples, these are discussed here.
Standard hexagon
If all of the sides have the same length and all of the interior angles are the same size, a hexagon is said to be a regular hexagon. Moreover, the interior angle is 120 degrees. The regular hexagon has rotational symmetry of order six and six symmetrical lines.
learn more about hexagons,
https://brainly.com/question/3295271
#SPJ4
when group a loses an item or items to group b even though group a's population grew at a faster rate than group b's, the _______ paradox occurs.
Answers
When Group A loses an item or items to Group B even though Group A's population grew at a faster rate than Group B's, the Simpson's Paradox occurs.
This statistical anomaly happens when a trend appears in different groups of data, but disappears or reverses when the groups are combined. It is crucial to consider the context and variables involved when analyzing data, as the Simpson's Paradox may lead to incorrect conclusions if only aggregate data is examined.
This paradox serves as a reminder to always investigate the underlying factors that may influence statistical results.
Learn more about Simpson's paradox at
https://brainly.com/question/31679249
#SPJ11
I don’t know how to answer this ?

Answers
Answer:
36 + 72 + 36 = ?
Step-by-step explanation:
Answer:
AB and AC are equal because the triangle is an isosceles triangle
Step-by-step explanation:

The numbers in this sequence increase by 12 each time
24
36
48
60
The sequence is continued with the same rule.
Which number in the sequence will be closest to 100?
Answers
Ben reads 6 books in ten days what fraction of a book did Ben read each day
Answers
Evaluate the algebraic expression for the given values of x = 3 and y = 4. Tx - 2y - 1 = I
Answers
Answer:
7 or -9, dependent on if 2y is or is not negative
Step-by-step explanation:
If 2y is NOT negative
2(4)-1=i
8-1=i
i=7
If 2y IS negative
-2(4)-1=i
-8-1=i
i=-9
27°
15
Solve for b.
40°
b
b = [ ?
Round your final answer
to the nearest tenth.

Answers
10.59 is the value of the given side b.
In our case, we know that side A has a length of 15 units and is opposite angle A, which measures 27 degrees.
Using the sine rule, we can write:
b/sin(27°) = 15/sin(40°)
To find the value of b, we can rearrange the equation:
b = (15 * sin(27°)) / sin(40°)
evaluate the trigonometric functions and calculate b:
b ≈ 10.59
Therefore, using the sine rule of the triangle, we find that the value of side b is approximately 10.59 units.
Learn more about triangles here:
https://brainly.com/question/2773823
#SPJ1
remainder
20 ) 740 please I’m failing math

Answers
Answer:
37
Step-by-step explanation:
there's no remainder
:) hope this helps
The highest common factor (HCF) of 28, 36, and 48 is
A) 4
B) 48
C) 756
D) 1008
Answers
Answer: 4
Step-by-step explanation: 756 and 1008 are not factors of any of them, 48 isn't a factor of 28 or 36
Express the inequality a < -0.18 using interval notation
Answers
Answer:
( -∞, -0.18 )
Step-by-step explanation:
a < -0.18
Interval Notation: ( -∞, -0.18 )
Given: < 2. Choose the solution set. {x | x < 10/11} {x | x > 10/11} {x | x > 22/5} {x | x < 22/5}.
Answers
The solution set is {x | x < \(\frac{22}{5}\)}.of the given evaluation.
What is a Solution Set?
The solution set of an equation is, however defined as the set of all solutions that satisfy the equation and since that set has no members the solution set is empty.
Given: \(\frac{5x}{11}\)\(< 2\)
= \(5x < 22\)
= \(x < \frac{22}{5}\)
Hence, the correct solution set is {x | x < \(\frac{22}{5}\)}.
To learn more about solution set :
brainly.com/question/9859818
#SPJ4
#12-15) Given its 3 sides, classify the triangle as right, acute, or obtuse. You must
show work to verify your answer.
12) 5, 7, 9
13) 5, 10, 5√3
14) √13, 10, 12
15) 16, 30, 34
Answers
It should be noted that 5, 7, 9 forms an obtuse triangle.
Also, 5, 10, 5√3 forms an acute triangle.
How to explain the trianglea² + b² = c²
5² + 7² = 25 + 49 = 74
9² = 81
Since 74 < 81, we know that 5, 7, 9 forms an obtuse triangle.
Again, we apply the Pythagorean theorem.
5² + (5√3)² = 25 + 75 = 100
(2√13)² = 52
Since 100 > 52, we know that 5, 10, 5√3 forms an acute triangle.
Applying the Pythagorean theorem:
(√13)² + 10² = 13 + 100 = 113
12² = 144
Since 113 < 144, we know that √13, 10, 12 forms an obtuse triangle.
Applying the Pythagorean theorem:
16² + 30² = 256 + 900 = 1156
34² = 1156
Since 1156 = 1156, we know that 16, 30, 34 forms a right triangle.
Learn more about Triangle on
https://brainly.com/question/17335144
#SPJ4
For every 3 people that prefer soda, 7 people prefer water. If 18 people prefer soda, how many prefer water?
Answers
Answer:
Step-by-step explanation:
w/18=7/3
w=126/3
w=42