Evaluate this expression.
5^2 +3 (8-2)
A. 28
B. 32
C. 43
D. 47
E. 168
Answers
Answer:
C. 43
Step-by-step explanation:
Related Questions
If gas is $4. 00/gal, how much does it cost to travel from Portland, Maine, to Orlando, Florida (a distance of 1,500 mi)? Give your answer to the nearest whole dollar. $.
Answers
Answer:
300
Step-by-step explanation:
It's gonna cost 300 dollars because you first find how many miles you can get for a gallon and that is 20 miles so you do 1500 miles divided by 20 miles which equals 75 then you do 75 times 4 which equals 300!
Please Mark Brainliest
What is the value of 1/4+1/8+1/2?
A. 3/8
B. 4/8
C. 6/8
D. 7/8
Answers
Answer:
D
Step-by-step explanation:
Convert all of the fractions' denominators so that they are 8. This is because 4,2, and 8's least common multiple is 8.
Remember that when multiplying the denominator, we must also multiply the numerator. So:
\(\frac{1}{2} * \frac{4}{4} = \frac{4}{8} \\\)
\(\frac{1}{4} *\frac{2}{2} =\frac{2}{8}\)
Since we are asked to add all of them, we can do that easily since all of the fractions now share a common denominator.
\(\frac{2}{8} +\frac{4}{8} + \frac{1}{8} = \frac{7}{8}\)
Therefore, the answer is D.
A manufacturer of widgets finds that the production cost, C, in dollars per unit is a function of the number of widgets produced. The selling price, S, of each widget in dollars is a function of the production cost per unit. C(x)=-0.1x^2+100 S(C)=1.4C
Answers
Answer:
I guess that you want to find the profit:
We have two equations:
the cost equation:
C(x) = -0.1*x^2 + 100.
And the selling equation, that is a vertical stretch of the cost equation by a factor of 1.4:
S(x) = 1.4*C(x) = 1.4*( -0.1*x^2 + 100.) = -0.14*x^2 + 140
Now, whit those two equations we can find the profit equation, that is defined as the difference between the selling price, and the cost:
P(x) = S(x) - C(x) = 1.4*C(x) - C(x) = (1.4 - 1)*C(x) = 0.4*C(x).
Then the profit is 0.4 times the initial cost.
P(x) = 0.4*( -0.1*x^2 + 100.) = -0.04*x^2 + 40
Answer:
D. S(C(x))= –0.14x^2+140; $108.50
Step-by-step explanation:
Cause the others are wrong
A card is drawn at random from a standard deck of cards. Find the probability of drawing:
1. A queen or a spade.
II. A black or a face card.
III. A red queen.
Answers
Given that a card is drawn at random from a standard deck of cards. We are asked to find the probabilities of
1) A queen or a spade.
2) A black or a face card.
3) A red queen.
This can be seen below;
Explanation
The formula for the probability of an event is given as;
\(\text{Pr(event) =}\frac{\text{number of events}}{\text{number of total possible outcomes}}\)For a given deck of cards, the number of total possible outcomes is 52 different cards. Next, we find the number of events for each case
\(\begin{gathered} n(\text{queen)}=4 \\ n(\text{spades)}=13 \\ n(\text{black)}=26 \\ n(\text{face card)=}12 \\ n(\text{red queen) =2} \end{gathered}\)Therefore we can find the probability in each case. Recall that "or" in probability implies we will add the values of the probabilities we are comparing.
1) A queen or a spade
\(Pr(\text{queen or spade)= }\frac{4}{52}+\frac{13}{52}=\frac{17}{52}\)Answer
\(Pr(\text{queen or spade)=}\frac{17}{52}\)
2) A black or a face card
\(Pr(black\text{ or }facecard)=\frac{26}{52}+\frac{12}{52}=\frac{38}{52}=\frac{19}{26}\)
Answer:
\(Pr(\text{black or facecard)=}\frac{\text{19}}{26}\)3) A red queen
\(Pr(A\text{ }red\text{ }queen)=\frac{2}{52}=\frac{1}{26}\)
Answer
\(Pr(A\text{ }red\text{ }queen)=\frac{1}{26}\)
Hello, can any one help me? Please

Answers
Answer:
d divided by 1/15 is o.75
Step-by-step explanation:
what is the difference in perimeters of one square that has a side length of 3/4 of an inch and another square that has a side length of 1/4 of an inch?
Answers
The difference in perimeters between the two squares is 2 inches.
Here, we have,
To find the difference in perimeters between two squares, we subtract the perimeter of the smaller square from the perimeter of the larger square.
Let's denote the side length of the larger square as S = 3/4 inch and the side length of the smaller square as s = 1/4 inch.
The perimeter of a square is given by the formula: P=4s, where s is the side length.
For the larger square with side length S = 3/4 inch, the perimeter P is:
P = 4 × 3/4
=3 inches
For the smaller square with side length s = 1/4 inch, the perimeter p is:
p = 4 × 1/4 =1 inch
The difference in perimeters is then:
Difference = P - p
so, we get,
Difference
=P - p
=3−1
=2 inches
Therefore, the difference in perimeters between the two squares is 2 inches.
Learn more about perimeter here:
brainly.com/question/397857
#SPJ4
You have a mortagege of $275,000
after down payment with an interest
rate of 3% for 30 years.
What does P, r,n, and t are equal to?

Answers
Answer:
Our calculator limits your interest deduction to the interest payment that would be paid on a $1,000,000 mortgage. Interest rate: Annual interest rate for this
Step-by-step explanation:
When the p-value is used for hypothesis testing, the null hypothesis is rejected ifa)p-value ≤ αb)α < p-valuec)p-value ≥ αd)p-value = 1 - α
Answers
If he p-value is used for hypothesis testing , then the Null Hypothesis is rejected if (a) p-value ≤ α .
In a hypothesis testing, the p-value represents the probability of observing a test statistic as extreme or more extreme than the one observed, provided that the null hypothesis is True.
The significance level, represented by "α" , is a pre-determined threshold which determines the level of evidence required to reject the null hypothesis.
If the p-value is less than or equal to α, this indicates that the observed test statistic is sufficiently unlikely to occur under the null hypothesis, and therefore the null hypothesis is rejected.
Therefore , the Null hypothesis is rejected if (a) p-value ≤ α .
The given question is incomplete , the complete question is
When the p-value is used for hypothesis testing, the null hypothesis is rejected if
(a) p-value ≤ α
(b) α < p-value
(c) p-value ≥ α
(d) p-value = 1 - α
Learn more about Hypothesis here
https://brainly.com/question/16261813
#SPJ4
The correct answer is a) p-value ≤ α. In hypothesis testing, the null hypothesis is typically assumed to be true initially. The p-value is used to determine the probability of observing a test statistic as extreme or more extreme than the one obtained from the data, assuming that the null hypothesis is true.
The significance level (α) is chosen beforehand and represents the maximum acceptable probability of rejecting the null hypothesis when it is actually true.
If the p-value is less than or equal to the significance level (p-value ≤ α), then the result is considered statistically significant and the null hypothesis is rejected. This implies that the observed effect is unlikely to have occurred by chance alone and that the alternative hypothesis is more likely to be true.
Learn more about p-value here:
https://brainly.com/question/30461126
#SPJ11
approximately how fast is a person located at the earth's equator traveling due to the rotation of the earth? hint: a person located at the equator will go once along the circumference of a circle with radius equal to the radius of the earth in a time interval equal to 24 hours. speed is equal to distance traveled divided by the time interval.
Answers
The speed of the person located at earth's equator traveling due to rotation is, 1670 km/hr.
The person at equator traveling due to it's rotation will cover one complete round of earth in 24 hours. Hence the distance travelled is the circumference of the earth.
The radius of the earth is, 6 378.1 kilometers.
The circumference can be calculated as, 2×π×R
Using R = 6 378.1 kilometers,
Circumference = 2×π×6 378.1 kilometers
Circumference = 40090.91 kilometers.
The distance traveled = 40090.91 kilometers.
Time taken is 24 hrs.
Hence speed = distance/time
Speed = 40090.91/24
Speed = 1670 km/hr
The speed of the person is 1670 km/hr.
To know more about the speed, here
brainly.com/question/29775794
#SPJ4
Please give me correct answer fast

Answers
The table C) contains point representing the function f(x) = -x/4+2.
Function in mathThe definition of a function in mathematics can also be interpreted as a relation that connects each member of x in a set called the domain (domain) with a single value f(x) from a second set called the codomain (codomain).
The set of values obtained from these relations is called the range. A function is a rule that connects each element in a set, so that a function can be said to be a special part of a relation.
According to the question above:
To prove each points in table C:
x=0
f(0) = -x/4+2. = -(0) /4+2=2
x=4
f(4) = -x/4+2.=-(4) /4+2=1
x=6
f(6) = -x/4+2= -6/4+2=-3/2+4/2=1/2
x=8
f(8) = -x/4+2=-8/4+2=-2+2=0
Learn more about function in math at
https://brainly.com/question/15096947
#SPJ1
help this is easy middle school question

Answers
Answer:
5
Step-by-step explanation:
Five is the LCM or 35 and 15, since both can be divided by 5.
Hope this helped <3
Is it possible to define all the terms in geometry including the three terms which are point line and plane?
Answers
A point, a line, and a plane are undefined words in geometry.
A point is defined as a place without regard to size. A plane runs infinitely in two dimensions,A line is defined as anything that extends eternally either in direction but has no width.What is a geometry?A subfield of mathematics called geometry examines the dimensions, placements, angles, and sizes of objects.
2D Geometric Shapes2D shapes, which include flat shapes such squares, circles, and triangles, are a subset of flat geometry. The length and width are the only 2 dimensions of these forms.
3D Geometric ShapesA solid figure, object, or shape with three dimensions—length, breadth, and height—is referred to as a three-dimensional shape in geometry. Three-dimensional shapes contain thickness or depth, in contrast to two-dimensional shapes.
AngleIn terms of geometry, an angle is the shape created when two rays intersect at a single terminal. The sign is used to denote an angle. A protractor is used to measure angles in degrees (°).
To know more about geometry, here
https://brainly.com/question/24236629
#SPJ4
What value of z should we use when making a 93% confidence interval for p? A. 1.48 B. It's impossible to make a 93% CI. C. 2.70 D. 1.81
Answers
The value of z that should be used when making a 93% confidence interval for p is Z=1.81 that is option D.
The z score is a measure of how many standard deviations a raw score is below or above the population mean. It will be positive if the value is more than the mean and negative if it is less than the mean. It is often referred to as the standard score. It represents the number of standard deviations an entity has from the mean.
To utilise a z-score, both the mean and the population standard deviation must be known. The z score calculates the likelihood of a score occuring within a standard normal distribution. It also allows us to compare scores from various samples. A table for the values of, representing the values of the cumulative distribution function of the normal distribution, is known as a
At 93% confidence, the significance level is,
ɑ= 1-0.93
ɑ= 0.07
Divide alpha by 2,
ɑ/2= 0.07/2= 0.035
Now, from the ‘normal probability’ table, the z value corresponding to the inverse probability of 0.035 is 1.81.
As a result, the z value is 1.81 at 93% confidence level.
z= 1.81
The value for z score is 1.81
Learn more about Confidence interval :
https://brainly.com/question/27325376
#SPJ4
Please Help Me!
In the figure, p || 9. Find m<21.
a, m<1 = 63
b. m<1 = 52
c.m<1 = 38
d. m<1 = 65

Answers
Answer: B or 52
Step-by-step explanation: I will explain later
Write a recursive formula for the arithmetic sequence:a={12,17,22,...}a_1=Answera_n = a_{n-1} + Answer

Answers
1) A Recursive formula refers always to the previous term.
2) In this Arithmetic Sequence, the common difference is 5, the first term is 12. So we can set the following Arithmetic Sequence:
\(\begin{gathered} a_{1}=\textbf{12} \\ a_2=12+5n \\ a_n=a_{n-1}+\textbf{5n} \end{gathered}\)Thus, this is the answer.
Consider a triangle ABC like the one below. Suppose that B= 60°, C=76°, and a=33. (The figure is not
drawn to scale.) Solve the triangle.
Round your answers to the nearest tenth.
If there is more than one solution, use the button labeled "or".

Answers
The values of ∠A=44° , b=42.1 units and c=46.1 units for the triangle ABC in which ∠B=60° , ∠C=76° and a=33 is given was found using sine-law.
What is sine law?
Any triangle with a side and its opposite angle known can be solved using the sine rule (not just right-angled triangles). The sine rule is given by \(\frac{Sin A}{a} =\frac{sin B}{B} =\frac{Sin C}{C}\) . The other version of this is \(\frac{a}{Sin A} =\frac{b}{Sin B} =\frac{c}{Sin C}\). Use the Sine Rule version where the lengths are on top if you need to determine the length of a side. Use the Sine Rule version where the lengths are on top if you need to determine the length of a side.
Here given values of ΔABC, ∠B=60° , ∠C=76° and a= 33
We know that by angle sum property, ∠A + ∠B + ∠C =180°
∴∠A + ∠B + ∠C =180°
∠A + 60° + 76° =180°
∠A = 180 - 60 - 76
∠A=44°
According to Sine law, \(\frac{a}{Sin A} =\frac{b}{Sin B} =\frac{c}{Sin C}\)
Taking \(\frac{a}{Sin A} =\frac{b}{Sin B}\) , we can find side b.
\(\frac{a}{Sin A} =\frac{b}{Sin B}\)
\(\frac{33}{Sin 44} =\frac{b}{Sin 60}\)
\(\frac{33}{0.6946} = \frac{b}{0.866}\)
b = \(\frac{33}{0.6946} x 0.866\)
=42.143 units
On rounding off to nearest tenths value of b=42.1 units
Taking \(\frac{a}{Sin A} =\frac{c}{Sin C}\) , we can find side c.
\(\frac{a}{Sin A} =\frac{c}{Sin C}\)
\(\frac{33}{Sin 44}= \frac{c}{Sin 76}\)
\(\frac{33}{0.6946} =\frac{c}{0.970}\)
c = \(\frac{33}{0.6946} x 0.970\)
c = 46.084
On rounding off to nearest tenths value of c=46.1 units
The values are ∠A=44° , b=42.1 units and c=46.1 units.
To know more about sine-law, visit:;
https://brainly.com/question/27174058
#SPJ9
yall some hot cheetos with some fresh lime juice and Tajin be bussin P.S im eating some right now tehheee
what yall fav snack combo
Answers
Answer:
ruffles classic + those two bite cupcakes literally best thing to exist
Step-by-step explanation:
Answer:
Honestly, twinkies with twinkies
Step-by-step explanation:
#WhyNot
Landon analyzed data and found that the correlation coefficient for their line of best fit was -0.85. Marco analyzed a different set of data and found a correlation coefficient of 0.85. Marco states that since 0.85 is greater than -0.85, his data points have a better line of best fit than Landon. Is Marco correct? Why, or why not?
Answers
Marco's data points have a better line of best fit based on a comparison of Correlation coefficients.
Marco is incorrect in stating that his data points have a better line of best fit than Landon based solely on the comparison of correlation coefficients. The magnitude of the correlation coefficient alone does not determine the quality or strength of the line of best fit.
The correlation coefficient measures the strength and direction of the linear relationship between two variables. It ranges from -1 to +1. A positive correlation coefficient (such as 0.85) indicates a positive linear relationship, while a negative correlation coefficient (such as -0.85) indicates a negative linear relationship. The closer the correlation coefficient is to -1 or +1, the stronger the relationship. A correlation coefficient of 0 indicates no linear relationship.
In the case of Landon and Marco, both correlation coefficients have the same absolute value of 0.85, suggesting a strong linear relationship. However, the negative sign for Landon's correlation coefficient indicates a negative linear relationship, while the positive sign for Marco's correlation coefficient indicates a positive linear relationship.
The comparison between -0.85 and 0.85 should not be made in terms of greater or lesser quality of the line of best fit. The choice of a positive or negative correlation depends on the context and nature of the variables being analyzed.
The appropriateness of the line of best fit and the goodness-of-fit of the model should be evaluated based on additional factors such as the data points' distribution around the line, residuals, and the overall context of the analysis. These aspects provide more comprehensive insights into the quality of the fit and the reliability of the relationship being represented.
Therefore, Marco's data points have a better line of best fit solely based on a comparison of correlation coefficients. The interpretation of the correlation coefficient requires considering the nature of the variables and other factors influencing the analysis.
To know more about Correlation coefficients.
https://brainly.com/question/30634313
#SPJ11
The figure is not drawn to scale. PQ and MN are straight lines. Find
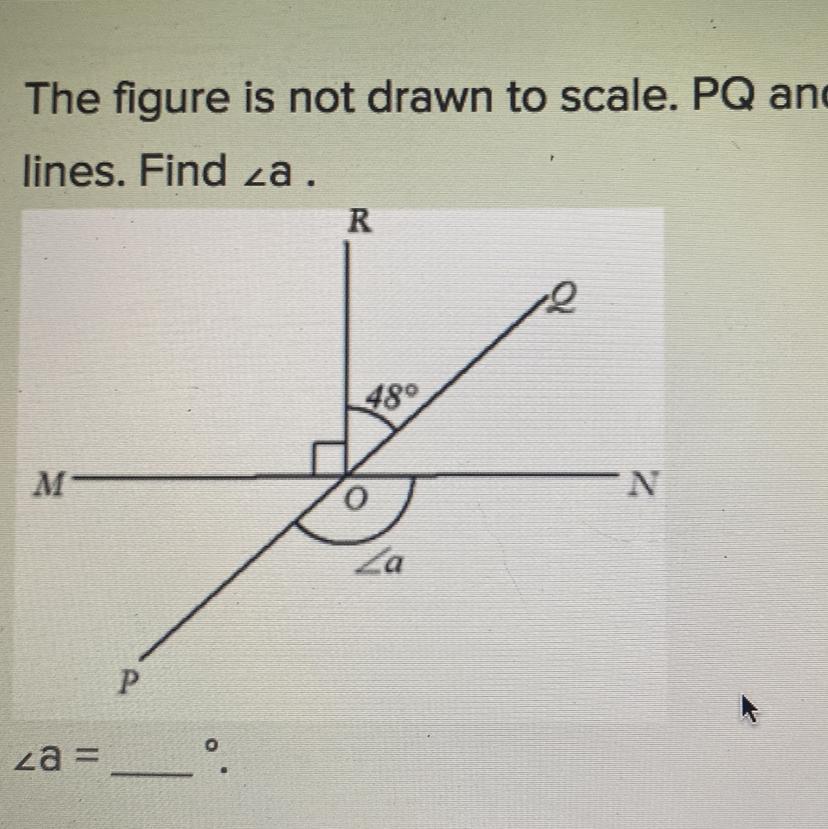
Answers
Answer:
a = 138
Step-by-step explanation:
Notice that from the figure, we can see that ∠MOQ and ∠PON are vertical angles, which means that by definition, they're congruent in measure.
∠MOQ = ∠MOR + ∠ROQ = 90 + 48 = 138°
So, this means that ∠PON is also equal to 138, which means a = 138.
Thus, the answer is a = 138.
~ an aesthetics lover
Given that the solutions of the previous question are W1= 20.27 and W2=-17.27, please answer question 9

Answers
Since we're talking about dimensions, the only solution that makes sense in the context of the problem is W1, because we cannot have negative measurements.
There 7 ducklings .they sleep in 1 large nest .write and solve an equation that shows how many ducklings sleep in the nest
Answers
Answer:
7 ÷ 1 = 7
Step-by-step explanation:
Answer:
I think
Step-by-step explanation:
I think you are subtracting
How much money do I need now if I am going to recieve $5000 every 6 months (starting in 6 months) for 10 years if the interest rates are 4%/a compounded semi-annually?
Answers
By using the compound interest model, the initial deposit required to receive $ 5 000 every 6 months is $ 125 000.
How many money should be deposited in the beginning to receive a certain amount periodically
In this problem we must apply the compound interest model, which represent a periodic accumulation of interest according to the following formula:
C' = C · (1 + r/100)ˣ (1)
Where:
C - Initial depositr - Interest rateC' - Resulting moneyx - Period indexIf we know that x = 1, r = 4, C = x and C' = x + 5 000, then the initial deposit is:
x + 5 000 = x · (1 + 4/100)
x + 5 000 = 1.04 · x
0.04 · x = 5 000
x = 125 000
By using the compound interest model, the initial deposit required to receive $ 5 000 every 6 months is $ 125 000.
To learn more on compound interest: https://brainly.com/question/14295570
#SPJ1
Q(3,5),R(3,1),S(-1,1),T(-1,5) Determine weather QRST is a rhombus, rectangle, or a square
Answers
Answer:
1/2
Step-by-step explanation:
1.0 :1/2
I used a graphing calculator
The answer is a square
y varies inversely with x. Write an equation relating x and y.
Then find the indicated value. Show your work.
y = 3 when x = 8. Find the value of y when
x = 6.
y = 9 when x = 6. Find the value of x when
y = 4.
y= 1.5 when x = 14. Find the value of y when
x = 9.
y = 20 when x = 10. Find the value of x when
y = 25.
Answers
The equation of variation is xy = k.
The required values are given below.
What is proportional relationship?A proportional relationship is a relationship between two expressions and where changes in one expression means some constant change in the other expression as well. Generally, it is represented as x/y = k, where x and y are two expressions and k is constant.
Given:
y inversely varies as x.
That means, y ∝ 1/x.
So, y = kx, where k constant of variation.
Then, x × y = k
When y = 8, x = 3.
k = 3 × 8 = 24
So, the equation of variation is xy = 24.
When x = 6,
6y = 24
⇒ y = 4
When y = 9, x = 6.
k = 6 × 9 = 54
So, the equation of variation is xy = 54.
When y = 4,
4x = 54
⇒ x = 27/2
When y = 1.5, x = 14.
k = 1.5 × 14 = 21
So, the equation of variation is xy = 21.
When x = 9,
9y = 21
⇒ y = 7/3
When y = 20, x = 10.
k = 20 × 10 = 200
So, the equation of variation is xy = 200.
When y = 25,
25x = 200
⇒ x = 8
Therefore, the values are given above.
To learn more about the proportional relationship;
brainly.com/question/28777033
#SPJ1
statistics the art and science of learning from data 4th edition
Answers
"Statistics: The Art and Science of Learning from Data" (4th edition) is a valuable resource for understanding and applying statistical principles, providing insights into data analysis and decision-making processes.
Statistics is the art and science of learning from data. It involves collecting, organizing, analyzing, interpreting, and presenting data to gain insights and make informed decisions. In the 4th edition of the book "Statistics: The Art and Science of Learning from Data," you can expect to find a comprehensive exploration of these topics.
This edition may cover important concepts such as descriptive statistics, which involve summarizing and displaying data using measures like mean, median, and standard deviation. It may also delve into inferential statistics, which involve making inferences and drawing conclusions about a population based on a sample.
Additionally, the book may discuss various statistical techniques such as hypothesis testing, regression analysis, and analysis of variance (ANOVA). It may also provide real-world examples and case studies to illustrate the application of statistical methods.
When using information from the book, it is important to properly cite and reference it to avoid plagiarism. Be sure to consult the specific edition and follow the guidelines provided by your instructor or institution.
In summary, "Statistics: The Art and Science of Learning from Data" (4th edition) is a valuable resource for understanding and applying statistical principles, providing insights into data analysis and decision-making processes.
Know more about Statistics here,
https://brainly.com/question/31538429
#SPJ11
please help please help

Answers
Answer:
C.) =
Step-by-step explanation:
the absolute value of 5 is 5, and the absolute value of -5 is 5, so they will be equal
Answer:
=
Step-by-step explanation:
The absolute value of a number is how far the number is from zero on a number line.
Both 5 and -5 are 5 units from zero on a number line, so
|5| = |-5| since |5| = 5 and |-5| = 5.
Draw a rectangle that is 4 squares long and 1 /2 of a square wide. Then add up the partial squares to find the area. Multiply to check your answer. ( i need a model )
Answers
According to the information, the area of a rectangle with the base of 4 squares (cm) and the height of 1/2 square (cm) would be: 2 cm²
How to find the area of this figure?To find the area of this rectangle we must take into account its dimensions. In this case, we have 4 squares (cm) (suppose each one is 1cm) long and 1/2 (cm) (0.5) long.
According to the above, we only have to multiply these values and we will have found the area of the rectangle:
4 * 0.5 = 2So the area of this rectangle would be 2cm².
Learn more about the area of rectangles in: https://brainly.com/question/29123947
#SPJ1
Find the orthogonal projection of v = 9 onto the plane-2x1-x2-3x3 = 0 7 projection =
Answers
The orthogonal projection of the vector v = [9] onto the plane -2x1 - x2 - 3x3 = 0 is [3, 1, -1]. To find the orthogonal projection, we need to find a vector in the plane that is closest to v.
The projection vector can be obtained by subtracting the component of v that is orthogonal to the plane from v itself.
The equation of the plane -2x1 - x2 - 3x3 = 0 can be rewritten as [2, 1, 3] ⋅ [x1, x2, x3] = 0, where ⋅ denotes the dot product. This equation represents the normal vector to the plane.
Next, we can find the component of v that is orthogonal to the plane by projecting v onto the normal vector. The projection of v onto the normal vector is given by (v ⋅ n) / ||n||^2 * n, where ||n|| denotes the magnitude of the normal vector.
Plugging in the values, we have (v ⋅ n) / ||n||^2 * n = (9 ⋅ [2, 1, 3]) / ||[2, 1, 3]||^2 * [2, 1, 3] = (9 ⋅ 5) / 14 * [2, 1, 3] = [45/14, 45/28, 135/14].
Finally, we subtract this component from v to obtain the orthogonal projection: [9] - [45/14, 45/28, 135/14] = [9 - 45/14, 0 - 45/28, 0 - 135/14] = [3, 1, -1].
Learn more about orthogonal projection here:
brainly.com/question/31185902
#SPJ11
Prove by mathematical induction each of the following identities: (a) 1+2+3+...+n= n(n+1) 2 (b) 1² +2²+3²+...+ n² = n(n + 1)(2n + 1) 6 (c) 1·2+2.3+3.4++ n(n + 1) = n(n+1)(n+2) 3 - (d) 1²+ 3² +5² + ... + (2n − 1)² = n(4n² − 1) 32 3 (e) 1+2.2+3.2²+...+n2"-1 = = (n-1)2" + 1. 1 1 1 1 + + + ... + 1.3 3.5 5.7 (2n-1)(2n + 1) n 2n + 1
Answers
In this problem, we are asked to prove several identities using mathematical induction. The identities are: (a) 1+2+3+...+n = n(n+1)/2, (b) 1² + 2² + 3² + ... + n² = n(n+1)(2n+1)/6, (c) 1·2 + 2·3 + 3·4 + ... + n(n+1) = n(n+1)(n+2)/3, (d) 1² + 3² + 5² + ... + (2n-1)² = n(4n²-1)/3, and (e) 1+2·2+3·2²+...+n²−1 = (n-1)2^n + 1.
To prove these identities by mathematical induction, we typically follow a two-step process. First, we prove the base case, which is usually n = 1. We substitute n = 1 into each identity and show that the base case holds true. Second, we assume the identity is true for some arbitrary positive integer k and then prove that it holds for k+1.
For each identity, we will use the mathematical induction process to prove it. We will show that the base case holds true, and then assume the identity is true for some k and prove it for k+1. By successfully completing both steps, we can conclude that the identity holds true for all positive integers n.
Learn more about mathematical induction here: brainly.com/question/29503103
#SPJ11
3x + 4 =22 what is the value of x
Answers
Answer:
Step-by-step explanation:
I’m pretty sure x= 10
Answer:
x=6
Step-by-step explanation: