Evaluate -2x^2 2y, if x = -3 and y = -1.
Answers
ANSWER is 16.
look at the photo to see the step by step equation :)
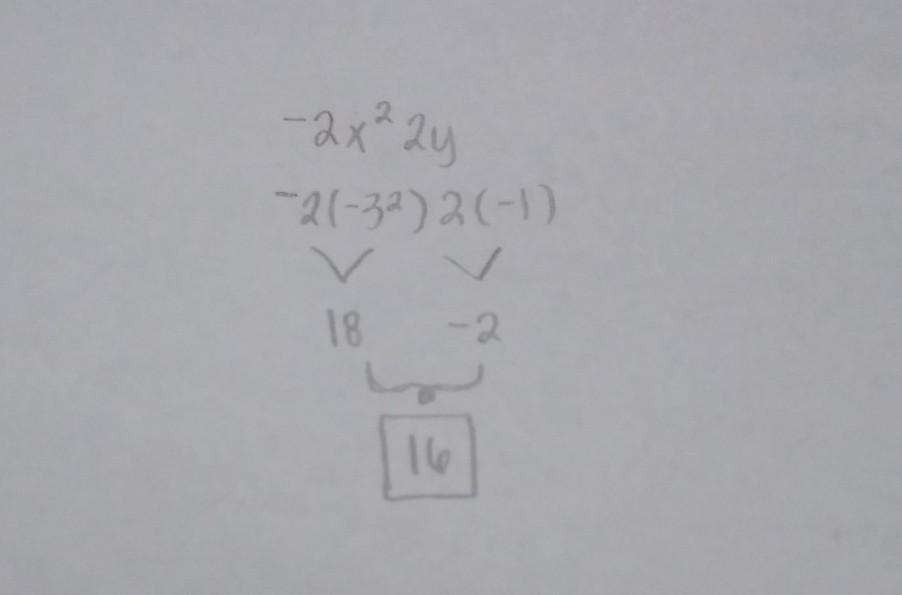
Related Questions
The electric field of a dipole situated at the origin and pointing in the z direction is given by where p- pl is the magnitude of the dipole moment and (r, θ) are the usual spherical coordinates.
Answers
The answer of the question is ,field along an arbitrary path gives
= - (p cosθ/4πεr) and,
the work done to move a charge Q from P is θ = arccos(z/r).
What is Work done?Work done is defined as energy transferred to or from object when force is applied to it, causing it to move certain distance in direction of the force.
(a) To integrate the electric field along an arbitrary path, we need to use the definition of potential difference, which is the negative of the line integral of the electric field:
V(F) = - ∫F Edl
where V(F) is the potential difference between the endpoints of the path, F is the path, E is the electric field, and dl is an infinitesimal element of the path.
the electric field in the spherical coordinates are given by:
Edipole (r, 0) = (P/4πε) [(2cosθ/r^2) i + (sinθ/r^2) j]
where θ = 0 on the z axis.
F = r(θ) i + r(φ)sinθ j
where r(θ) and r(φ) are the functions of θ and φ that describe the path.
Then, we can express dl in terms of these functions:
dl = dr(θ) i + r(θ) dφ j
Substituting the expression into line integral, we get:
Vdipole = - ∫F Edl = - ∫θ1θ2 ∫φ1φ2 Edr(θ) - Er(φ)sinθ dθ dφ
Integrating with the respect to φ , we get:
Vdipole = - ∫θ1θ2 [(P/4πε) (2cosθ/r^2) r(φ)]dθ
= - (P/4πε) [(r(φ)/r^2)|θ1θ2] ∫θ1θ2 2cosθ dθ
= - (P/2εr) [cosθ1 - cosθ2]
where r = r(θ1) = r(θ2) is the constant radius of the path.
Substituting θ1 = 0 and θ2 = θ, we get:
Vdipole = - (P/2εr) cosθ
= - (p cosθ/4πεr)
(b ) To find the work done to move a charge Q from P to Q, we need to use the formula for potential difference:
W = Q[V(Q) - V(P)]
where W is the work done, Q is the charge, and V(Q) and V(P) are the potentials at the endpoints of the path.
For a charge Q moved from P = √(x + y) to Q = - (ŷ+2), the potential difference is:
V(Q) - V(P) = - (p cosθ/4πεr(Q)) + (p cosθ/4πεr(P)))
where r(Q) and r(P) are the distances from the dipole to the endpoints of the path.
Substituting the given values for P and Q, we get:
r(P) = √(x^2 + y^2), r(Q) = √[(y+2)^2 + x^2]
θ = arccos(z/r).
To know more about Force visit:
https://brainly.com/question/13014979
#SPJ1
* The complete question is :
The electric field of a dipole situated at the origin and pointing in the z direction is given by
Edipole (r, 0) =P Απεργ
(2 cos 0 + + sin 00),
where p = [p] is the magnitude of the dipole moment and (r, 0) are the usual spherical coordinates.
(a) Integrate the field along an arbitrary path and show that V(F) = - [Ē - dī gives,
Vdipole (r, 0) =p cos 0 Απεργ
Note: You are requied to compute the indefinite integral and so no limits are required.
(b) Find the work done to move a charge Q from P = √(x + y) to Q = -(ŷ+2).
In nop, the measure of zp=90°, the measure of zn=39, and pn = 72 feet. find the length of op to the nearest tenth of a foot?
Answers
The length of OP to the nearest tenth of a foot is approximately 41.5 feet
To find the length of OP, we can use the Pythagorean theorem since we have a right triangle.
OP^2 = PN^2 - ON^2
First, we need to find ON using the trigonometric ratio of tangent.
tan(39) = ON/PN
ON = PN * tan(39)
ON = 72 * tan(39)
ON ≈ 53.4 feet
Now we can plug in our values:
OP^2 = 72^2 - 53.4^2
OP^2 ≈ 1720.84
OP ≈ 41.5 feet (rounded to the nearest tenth of a foot)
Therefore, the length of OP to the nearest tenth of a foot is approximately 41.5 feet.
To know more about length refer here
https://brainly.com/question/9842733#
#SPJ11
What is m∠A?
A- (3x+13)°
B- (x-8)°
C- x°

Answers
Answer:
216°.
Step-by-step explanation:
The work is in the photo, I suppose.

Converting Real Life Scale.. -Page 2-
NEED HELP ASAPPP 50 POINTS
(picture is linked belowww)
tysm like fr <33

Answers
The table with the scale measurements is given by the image shown at the end of the answer.
How to obtain the measurements?The measurements are obtained applying the proportion given for each table.
The symbols are given as follows:
': feet.'': inches.For the first table, we have that every inch on the table represents one feet in real life, hence:
2'' on the paper represents 2' in real life.2' on the paper represents 24' in real life. (as one feet = 12 inches, hence 24 inches = 24 feet according to the scale).0.5'' on the paper represents 0.5' in real life.9'' on the paper represents 9' in real life.For the second table, we have that every inch on the paper represents two feet in real life, hence the measurements are given as follows:
2'' on the paper represents 4' in real life.2' on the paper represents 48' in real life.0.5'' on the paper represents 1' in real life.9'' on the paper represents 18' in real life.More can be learned about scale measurements at https://brainly.com/question/29229124
#SPJ1

A Bluetooth speaker in the shape of a triangular pyramid has a height of 12 inches. The area of the base of the speaker is 10 square inches.
What is the volume of the speaker in cubic inches?
A.20
B.40
C.60
D.80
Answers
Answer:
The correct option is B. 40.
Step-by-step explanation:
To calculate the volume of a triangular pyramid, you need to know the height and the area of the base. In this case, the height of the triangular pyramid is given as 12 inches, and the area of the base is given as 10 square inches.
The formula for the volume of a triangular pyramid is:
Volume = (1/3) * Base Area * Height
Substituting the given values:
Volume = (1/3) * 10 square inches * 12 inches
Volume = (1/3) * 120 cubic inches
Volume = 40 cubic inches
(-25) devided (-5).

Answers
Answer:
Step-by-step explanation:
Here you go mate
step 1
(-25)/(-5)
step 2
(-25)/(-5) divide the equation by 5
answer
=5
Answer: 5
Step-by-step explanation:
Multiplying or dividing a negative by a negative results in a positive.
\((-10)/(-2)=5\)
Multiplying or dividing a negative by a positive results in a negative.
\((-10)/(2)=-5\)
Multiplying or dividing a positive by a negative results in a negative.
\((10)/(-2)=-5\)
Multiplying or dividing a positive by a positive results in a positive.
\((10)/(2)=5\)
Thus, because -25 and -5 are both negatives, the answer must be positive.
what is the largest number of comparisons needed to perform a binary search on an array with 42 elements?
Answers
In a binary search, the number of comparisons needed is determined by the number of elements in the array. In each comparison, the search range is halved, and the process continues until the target element is found or the search range becomes empty.
Since a binary search divides the search range in half with each comparison, the maximum number of comparisons needed is equal to the number of times the search range can be halved until it becomes empty.
In the case of an array with 42 elements, the maximum number of comparisons needed is given by the formula:
\(\( \lceil \log_2(42) \rceil \)\)
Where \(\( \log_2 \)\) represents the logarithm to the base 2, and \(\( \lceil x \rceil \)\) denotes rounding up to the nearest integer.
Evaluating the expression:
\(\( \lceil \log_2(42) \rceil = \lceil 5.392317 \rceil = 6 \)\)
Therefore, the largest number of comparisons needed to perform a binary search on an array with 42 elements is 6.
To know more about logarithm visit-
brainly.com/question/30426668
#SPJ11
Which are correct representations of the inequality –3(2x – 5) < 5(2 – x)? Select two options. x < 5 –6x – 5 < 10 – x –6x + 15 < 10 – 5x A number line from negative 3 to 3 in increments of 1. An open circle is at 5 and a bold line starts at 5 and is pointing to the right. A number line from negative 3 to 3 in increments of 1. An open circle is at negative 5 and a bold line starts at negative 5 and is pointing to the left.
Answers
The correct representations of the inequality -3(2x - 5) < 5(2 - x) include the following:
-6x + 15 < 10 - 5xAn open circle is at 5 and a bold line starts at 5 and is pointing to the right. What is an inequality?An inequality can be defined as a mathematical relation that is typically used for comparing two (2) or more numerical data and variables in an algebraic equation based on any of the following arguments (symbols):
Less than (<).Less than or equal to (≤).Greater than (>).Greater than or equal to (≥).Next, we would evaluate and simplify the given inequality in order to determine the solution to this algebraic equation as follows:
-3(2x - 5) < 5(2 - x)
Opening the bracket, we have:
-6x + 15 < 10 - 5x (correct representation)
Next, we would rearrange the algebraic equation by collecting terms:
-6x + 5x < 10 - 15
-x > -5
x > 5 (correct representation)
Read more on inequality here: https://brainly.com/question/13702369
#SPJ1

Write an
expression that is equivalent to -0.5(20f – 16).
Answers
Answer:
- 10f + 8Step-by-step explanation:
Given expression:
- 0.5(20f - 16)Distribute and simplify:
-0.5(20f) - 0.5(- 16) = - 10f + 8Apply distributive law
a(b-c)=ab-ac\(\\ \tt\longmapsto -0.5(20f-16)\)
\(\\ \tt\longmapsto -0.5(20f)-0.5(-16)\)
\(\\ \tt\longmapsto -10f+8\)
how many groups of 1/5 are in 4 in fraction form
Answers
He has 16 flowers 1/8 of them are purple how many purple flowers does windy have
Answers
Answer:
2
Step-by-step explanation:
1/8 of 16 = 2
I need help:) kinda urgent but ILL MARK brainliest!! :)
Each garden design shown
requires the same amount of
fencing, in feet.How many feet of fencing must be purchased for either garden design
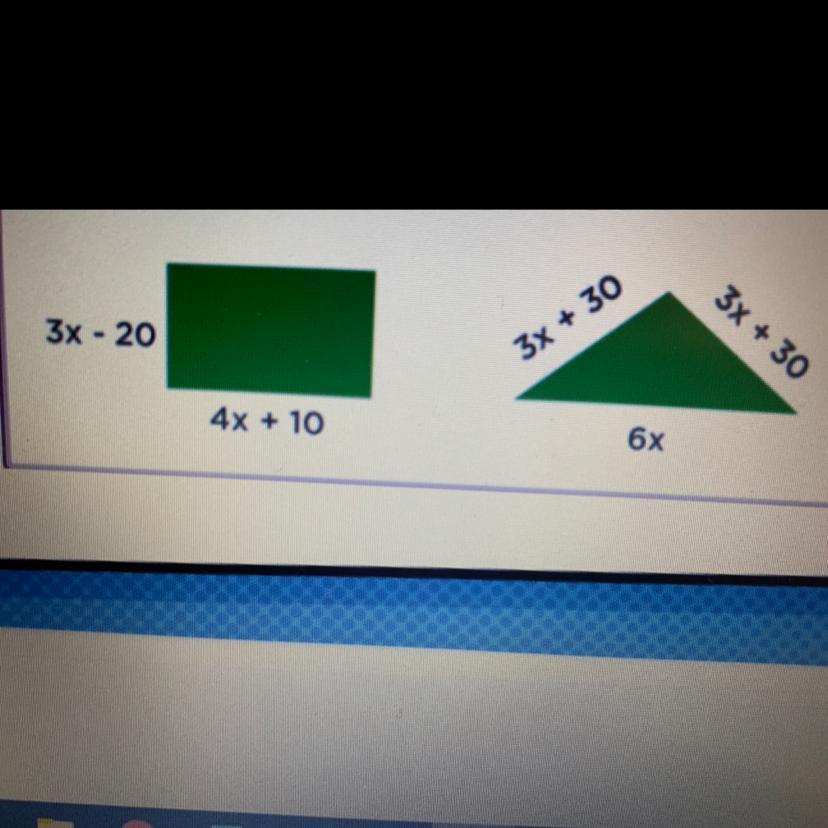
Answers
14x-20=12x+60
2x=80
X=40
George saves $163 a month. George saves $142 less each month than Lane. How much will Lane save in 2 years.
Answers
Answer:
504
Step-by-step explanation:
take 163 and subtract 142 then times by 24
3. If C is the input–output matrix for an economy with gross
production vector x, then C x is the net production vector
Answers
The statement "If C is the input-output matrix for an economy with gross production vector x, then Cx is the net production vector" is describing the relationship between the input-output matrix C, the gross production vector x, and the net production vector.
In an economy, the input-output matrix C represents the interdependencies between different sectors or industries. Each entry in the matrix represents the amount of output from one sector that is required as an input by another sector. The gross production vector x represents the total output produced by each sector without considering the interdependencies.
When we multiply the input-output matrix C by the gross production vector x, the result Cx represents the net production vector.
The net production vector takes into account the interdependencies between sectors by subtracting the inputs required from other sectors from the gross production. It gives us the final production available for consumption or further production.
In summary, by multiplying the input-output matrix C by the gross production vector x, we obtain the net production vector Cx, which accounts for the interdependencies between sectors and represents the final output available for consumption or further production.
Learn more about economy here: brainly.com/question/30131108
#SPJ11
The integral with respect to time of a force applied to an object is a measure called impulse, and the impulse applied to an object during a time interval determines its change in momentum during the time interval. The safety of a t-shirt launcher, used to help get crowds cheering at baseball games, is being evaluated. As a first step in the evaluation, engineers consider the design momentum of the launched t-shirts. The springs in the launcher are designed to apply a variable force to a t-shirt over a time interval of t1 = 0.5 s. The force as a function of time is given by F(t) = ať+ b, where a = –28 N/s2 and b = 7.0 N. The momentum of the t-shirt will be its initial momentum (po 0) plus its change in momentum due to the applied impulse: pf = po+SET+ F(t) dt. By applying the given time dependent function for F(t) and performing the integration, which of the following is the correct expression for Pf? ► View Available Hint(s) tl tl Pf= 0++)16 0+*+*+b) 0+++bt) 0++) ti Correct: We check that we have obtained the correct form of the integral by performing differentiation of gte + bt with respect to t, which gives at +6= F(t) as expected. Part B The units of the momentum of the t-shirt are the units of the integral si ti F(t) dt, where F(t) has units of N and t has units of S. Given that 1 N=1 kg. m/s",the units of momentum are: ► View Available Hint(s) - kg/s - kg.m/s3 - kg.m/s - kg•m/s2 Correct: The units of a quantity obtained by integration will be the units of the integrand times the units of the differential. Part C Evaluate the numerical value of the final momentum of the t-shirt using the results from Parts A and B.
► View Available Hint(s) kg.m Pf = 2.3 S
Answers
Part A: To find the expression for Pf, we need to integrate F(t) with respect to t over the given time interval.
Given that F(t) = ať + b, where a = -28 N/s^2 and b = 7.0 N, the integral can be calculated as follows:
Pf = po + ∫(F(t) dt)
Pf = po + ∫(ať + b) dt
Pf = po + ∫(ať dt) + ∫(b dt)
Pf = po + (1/2)at^2 + bt + C
Therefore, the correct expression for Pf is:
Pf = po + (1/2)at^2 + bt + C
Part B: The units of momentum can be determined by analyzing the units of the integral. Since F(t) has units of N (newtons) and t has units of s (seconds), the units of the integral will be N * s. Given that 1 N = 1 kg * m/s^2, the units of momentum are kg * m/s.
Therefore, the correct units of momentum are kg * m/s.
Part C: To evaluate the numerical value of the final momentum (Pf), we need to substitute the given values into the expression obtained in Part A. However, the initial momentum (po) and the time interval (t) are not provided in the question. Without these values, it is not possible to calculate the numerical value of Pf.
To know more about interval visit:
brainly.com/question/11051767
#SPJ11
$1500 at 9% for 2 years
Answers
Answer:$270
Step-by-step explanation:
I=PRT
Interest=principal times rate times time
Principal=1500
Rate=9%=0.09
Time=2
I=1500 times 0.09 times 2
I=1500 times 0.18
I=270
Interest=270
Total is 1500+270=1770 total paid
1. Write a congruence statement for the pair of triangles shown.
AUTS = ARST
AUTS = ASTR
AUTS = ARTS

Answers
Answer: ΔUTS ≅ ΔRST
Step-by-step explanation:
ΔTSU is congruent to ΔSTR, not ΔUTS
ΔUTS is congruent ΔRST not ΔRTS
ΔUTS ≅ ΔRST
Hope I helped!
4 pints, 3 cups = ____ fl oz.
Answers
Answer:
88
Step-by-step explanation:
4 pints = 8 cups
3 cups = 3 cups
8 cups + 3 cups = 11 cups
11 cups = 88 fl oz
Answer:
64 + 24 = 88 oz
Step-by-step explanation:
1 pint = 16 oz (4 x 16 = 64)
1 cup = 8 oz (3 x 8 =24)
when the angle of an incline with a block resting on it increases the normal support force? A) decreases B) increases C) stays the same
Answers
Answer:
normal force decreases
Step-by-step explanation:
N=mgcosθ, and cosine decreases as theta increases
consider joining our disc*rd server for unlimited hw help! we also have an active giveaway rn. code: RPEdT3erFm <3
Answer:
A) decreases
Step-by-step explanation:
As the angle of the incline increases, the normal force decreases, which decreases the frictional force. The incline can be raised until the object just begins to slide.
The expression (x - 6)2 is equivalent to
A. x2 - 36
B. x2 + 36
C. x2 - 12x + 36
D. x2 + 12x + 36
Answers
Answer:
x^2 -12x+36
Step-by-step explanation:
(x - 6)^2
(x-6)(x-6)
FOIL
x^2 - 6x-6x+36
Combine like terms
x^2 -12x+36
9a-b-2a-10b simplify this expression
A. -7a+11b
B. 11a+9b
C. -11a-9b
D. 7a-11b
please solve with explanation Q^Q
Answers
Step-by-step explanation:
answer is D
if u like it mrk me as brainliest
Answer: d) 7a-11b
Step-by-step explanation:
First collect all like terms
9a - 2a - 10b - b
= 9a - 2a = 7a
= -10b - b = -11b
Therefore the answer is 7a - 11b (D)
Show transcribed dataFind the general solution of the differential equation r ′(t)=(4−5t)i+10tj. (Use symbolic notation and fractions where needed. Give your answer in the form ⟨x(t),y(t),z(t)⟩.
Answers
The general solution of the differential equation is: r(t) = ⟨x(t),y(t),z(t)⟩ = ⟨(4t − (5/2)t^2), (5t^2), C⟩
The differential equation given is r ′(t)=(4−5t)i+10tj, where r(t) represents the position vector of a particle moving in a plane.
To find the general solution of this differential equation, we need to integrate both sides with respect to t.
Integrating the x-component of r ′(t), we get:
r(t) = ∫(4−5t) dt i + ∫10t dt j + C
r(t) = (4t − (5/2)t^2)i + (5t^2)j + C
where C is a constant of integration.
Therefore, the general solution of the differential equation is:
r(t) = ⟨x(t),y(t),z(t)⟩ = ⟨(4t − (5/2)t^2), (5t^2), C⟩
where C is an arbitrary constant.
Know more about the differential equations here:
https://brainly.com/question/1164377
#SPJ11
Find the smallest positive integer divisible by every positive integer less than or equal to ten.
please could you explain the method to me... i'm pretty confused
Answers
What is the range of the function f(x)= -6x^2 +5
Answers
Given:
\(f(x)=-6x^2+5\)If x=-2,
\(\begin{gathered} f(-2)=-6(-2)^2+5 \\ f(-2)=-6(4)+5 \\ f(-2)=-24+5 \\ f(-2)=-19 \end{gathered}\)If x=0,
\(\begin{gathered} f(0)=-6(0)^2+5 \\ f(0)=0+5 \\ f(0)=5 \end{gathered}\)Range of the function is:
\(\mleft\lbrace y|y\in\mathfrak{\Re },y\le5\mright\rbrace\)A square prism and a cylinder have the same height. the area of the cross-section of the square prism is 157 square units, and the area of the cross-section of the cylinder is 50π square units. based on this information, which argument can be made?
Answers
We can argue that the volume of square prism is greater than the volume of the cylinder.
To find the volume of a prism, we need to multiply the of area of base by the height. Since the height is the same for both the square prism and the cylinder, we can focus on comparing the areas of their respective cross-sections.
The area of the cross-section of the square prism is given as 157 square units. Since the cross-section is a square, we can find the side length by taking the square root of the area. So, the side length of the square is √157 units.
The area of the cross-section of the cylinder is given as 50π square units. Since the cross-section is a circle, we can find the radius by taking the square root of the area divided by π. So, the radius of the cylinder is √(50π/π) = √50 units.
Now, to compare the volumes, we need to calculate the volume of each shape. The volume of the square prism is equal to the area of the base multiplied by the height, which is (√157)^2 * height. The volume of the cylinder is equal to the area of the base (π * (√50)^2) multiplied by the height. Since the heights are the same, we can compare the volumes by comparing the areas of the bases.
Since (√157)^2 is greater than (√50)^2, we can conclude that the area of the base of the square prism is greater than the area of the base of the cylinder. Therefore, the volume of the square prism is greater than the volume of the cylinder.
In summary, based on the given information, we can argue that the volume of the square prism is greater than the volume of the cylinder.
Learn more about volume of square prism: https://brainly.com/question/28490327
#SPJ11
What Is the volume of the pyramid in the diagram?

Answers
Answer:
I think is A
Step-by-step explanation:
I hope it help
alfred and bonnie play a game in which they take turns tossing a fair coin. the winner of a game is the first person to obtain a head. alfred and bonnie play this game several times with the stipulation that the loser of a game goes first in the next game. suppose that alfred goes first in the first game, and that the probability that he wins the sixth game is m n , where m and n are relatively prime positive integers. what are the last three digits of m n ? (1993,
Answers
So, the last three digits of m*n is 001.
Let p be the probability that Alfred wins given that he goes first. Then, the probability that Bonnie wins given that she goes first is 1-p. Therefore, the probability that Alfred wins the second game given that Bonnie went first in the first game is 1-p. Similarly, the probability that Alfred wins the third game given that he went first in the second game is p, and so on.
Therefore, the probability that Alfred wins the sixth game given that he went first in the first game is:
p(1-p)(1-p)(p)(p)(p) = p^4 (1-p)^2
Since m and n are relatively prime, the last three digits of m*n are the last three digits of p^4 * (1-p)^2, which is the last three digits of p^4 and the last three digits of (1-p)^2. Since p is the probability of winning given that you go first, it is a number between 0 and 1. Therefore, the last three digits of p^4 and (1-p)^2 are 001, resulting in the last three digits of the final answer being 001.
Therefore, the last three digits of m*n is 001.
To learn more about probability
Visit; brainly.com/question/28525447
#SPJ4
Find an equation for the line tangent to the graph of the given function at the indicated point. 8 3) f(x): () = at at (4,2) X 1 4) f(x)=x2-x at (4, 12)
Answers
(a) tangent line to the graph of f(x) = x^3 at the point (4,2).
(b) equation of the tangent line to the graph of f(x) = x^2 - x at the point (4,12).
(a) To find the equation of the tangent line to the graph of f(x) = x^3 at the point (4,2), we need to find the slope of the tangent line at that point. We can do this by taking the derivative of f(x) with respect to x and evaluating it at x = 4. The derivative of f(x) = x^3 is f'(x) = 3x^2. Evaluating f'(x) at x = 4 gives us the slope of the tangent line. Once we have the slope, we can use the point-slope form of a linear equation to write the equation of the tangent line.
(b) Similarly, to find the equation of the tangent line to the graph of f(x) = x^2 - x at the point (4,12), we differentiate f(x) to find the derivative f'(x). The derivative of f(x) = x^2 - x is f'(x) = 2x - 1. Evaluating f'(x) at x = 4 gives us the slope of the tangent line. Using the point-slope form, we can write the equation of the tangent line.
In both cases, the equations of the tangent lines will be in the form y = mx + b, where m is the slope and b is the y-intercept.
Learn more about line tangent: brainly.com/question/30162650
#SPJ11
the combined perimeter of a circle and square is 16 cm. find the dimensions of the circle and square that produce a minimum total area.
Answers
the dimensions of the circle and square that produce a minimum total area are 1.12 and 2.24 respectively
given that
the combined perimeter of a circle and square is 16cm
let side length of the square is s
let radius of the circle with r
So, the perimeter (P) and the area (A) of the shape are:
P= 4s + 2\(\pi\)r
A = \(s^{2}\) + \(\pi\)\(r^{2}\)
given that perimeter is 16
so, 4s +2\(\pi\)r = 16
divide by 4
s +0.5\(\pi\)r = 4
s = 4 - 0.5\(\pi\)r
substitute s value in area
A = \((4-0.5\pi r)^{2}\) + \(\pi\)r
A = 16 - 4\(\pi\)r +0.25\((\pi r)^{2}\) +\(\pi\)\(r^{2}\)
A =16 - 4\(\pi\)r + (0.25 \(\pi ^{2}\) + \(\pi\))\(r^{2}\)
differentiate with respect to r
A' = 0 - 4\(\pi\) +2 (0.25 \(\pi ^{2}\) + \(\pi\))r
A' = - 4\(\pi\) +2 (0.25 \(\pi ^{2}\) + \(\pi\))r
now A' =0
- 4\(\pi\) +2 (0.25 \(\pi ^{2}\) + \(\pi\))r =0
2 (0.25 \(\pi ^{2}\) + \(\pi\))r = 4\(\pi\)
divide both sides by 2
(0.25 \(\pi ^{2}\) + \(\pi\))r = 2\(\pi\)
r = \(\frac{2\pi }{0.25\pi ^{2} +\pi }\)
r = \(\frac{2\pi }{\pi (0.25\pi +1)}\)
substitute \(\pi\) =3.14
r = 2/(0.25(3.14)+1)
r = 1.12
substitute r value in s
s = 4 - 0.5 * 3.14 *1.12
s =2.24
Hence, the dimensions of the circle and square that produce a minimum total area are 1.12 and 2.24 respectively
To learn more about area:
https://brainly.com/question/27683633
#SPJ4
Which shows the expression below simplified? (4.9 x 108) ÷ (7 x 105)
Answers
Hoping it helps...
Have a nice day!
