Evaluate 2x-y for x=3 and y= -2
A. 10
B. 14
C. 18
D. 20
Answers
2(3)-(-2)
6+2
8
Related Questions
PLEASE HELP ME!!!!!!!!!

Answers
Answer:
C
Step-by-step explanation:
Substitute x = -1 into \(f(x)=-\sqrt[3]{x-7}+3\) :
\(f(x)=-\sqrt[3]{-1-7}+3=-\sqrt[3]{-8}+3=2+3=5\)
Substitute x = 7 into \(f(x)=-\sqrt[3]{x-7}+3\) :
\(f(x)=-\sqrt[3]{7-7}+3=-\sqrt[3]{0}+3=0+3=3\)
Rewrite the equation in slope intercept form. 4x + 5y = 8
Answers
Answer:
y=-4/5+8/5, or y= -.8+1.6
Step-by-step explanation:
Slope intercept form-
y=mx+b
y=-4/5+8/5
what is the value of x ?

Answers
Step-by-step explanation:
2(2x - 6) + 2(x + 3) = 26
4x - 12 + 2x + 6 = 26
4x + 2x -12 + 6 = 26
6x - 6 = 26
6x = 26 + 6
6x = 32
x =32/6
x = 5.3333
Answer:
Step-by-step explanation:
2(2x -6) + 2(x + 3) = 26
4x - 12 + 2x + 6 = 26
6x - 6 = 26
6x = 32
x = 32/6= 16/3
If you are looking for a braniliest, if you get this right I will give one.
The question is, what app always says “gg”or “:)”
Answers
Answer:
amoung us
Step-by-step explanation:
Answer:
among us
Step-by-step explanation:
What is the least common multiple of numbers 20, 30 and 50?
Answers
Answer:300
Step-by-step explanation:
Answer:
answer is 300
hope it helps
plz mark as brainliest
THIS is due in a hour Justin gave the waiter a $2.25 tip at the restaurant. If his meal cost $12.50, what percent tip did he give?
Answers
2.25 / 12.50 = 0.18
0.18 x 100 = 18
18%
he gave 18% tip
Here's a graph of a linear function. Write the
equation that describes that function.
Express it in slope-intercept form.
Enter the correct answer.

Answers
Answer:
y= 3/2x + 1
Step-by-step explanation:
slope intercept form is y=mx+b. the m is the slope and the b is the y intercept. the y intercept is 1, where it crosses the y axis. the slope is 3/2 because from the y intercept which is 1, you go up 3 and over 2 right.
a coffee machine dispenses normally distributed amounts of coffee with a mean of 12 ounces and a standard deviation of 0.2 ounce. if a sample of 9 cups is selected, find the probability that the mean of the sample will be greater than 12.1 ounces. find the probability if the sample is just 1 cup.
Answers
Answer:i don't know really im just another student and i'm just doing this for the points my guy so don't be mad if you get a bad response
Step-by-step explanation:
1. I have no idea
At a rate of 42 miles per hour, it takes Henry 9 minutes to drive from the library to his house. Show how to find the distance that Henry traveled.
Answers
42 mph x .15 hours= 6.3 miles
Make a the subject of the formula v = u + at.
Hence, find the value of a when t = 4, u = 10 and v=50.
Answers
Step-by-step explanation:
v = u + at
v-u = at
a = (v -u)/t
When t = 4, u=10, v=50
a = (50-10)/4
a= 40/4
a = 10
You get a = 10

What must be subtracted from the product of 25 and 23 to equal 275
Answers
300 must be subtracted from the product of 25 and 23 to equal 275.
How do you dilate a triangle by?
Answers
To do dilatation a triangle by a scale factor of k, we have to multiply the x and y-value of each triangle point by k.
A coordinate plane is a system that graphs and describes the position of points and lines. It consists of horizontal (x) and vertical (y) axes.
We can perform dilatation for a point or line in a coordinate plane system based on specific criteria.
Dilation is a form of image transformation that produces a new image, which is larger, or smaller, based on a certain scale factor. The new image is the same in shape, but different in size.
The rule of dilatation:
\(D_{k}\)(x,y) = (kx, ky)
where \(D_{k}\) is the point of the new image and k is the scale factor.
When we want to dilate a triangle ABC, the result can be found by multiplying its original points with the scale factor.
For example:
Triangle ABC (-2,2), (-2,3), (1,2) is dilated by a scale factor of 2. The new triangle A'B'C' will be A’(-4,4), B’ (-4,6), and C’ (2,4).
Thus, to dilate a triangle by a scale factor of k, we have to multiply the x and y-value of each triangle point by k.
To learn more about dilatation, click here: brainly.com/question/16596053
#SPJ4
what value of x makes x/3 = 1.2/4 a proportion?
Answers
Answer:
0.9
Step-by-step explanation:
1.2/4 is 0.3. and 0.9/3 is 0.3. so... yeah
find the perimeter of GHI triangle
(on the bottom right corner)

Answers
The perimeter of triangle GHI is determined as 112.
What is the perimeter of triangle GHI?The perimeter of triangle GHI is determined by calculating the distance round the triangle GHI.
The given parameters include;
length GI = 52
length KI = length LI = 15
Length GL = GI - LI
GL = 52 - 15
GL = 37
Length GJ = GL = 37
Length GH = GJ + JH
GH = 37 + 4
GH = 41
Length HI is calculated as;
HI = HK + KI
HK = HJ = 4
HI = 4 + 15
HI = 19
The perimeter of triangle GHI is calculated as;
P = GI + GH + HI
P = 52 + 41 + 19
P = 112
Learn more about perimeter of triangles here: https://brainly.com/question/24382052
#SPJ1
How tell what the equation is if the vertical line is going through the y-axis?
Answers
Answer:
The equation of a vertical line in the graph, which is parallel to y-axis is x = a. The slope of a vertical line is infinity or undefined as it has no y-intercept and the denominator in the slope formula is zero.
Step-by-step explanation:
10. A line has equation y=3kx−2k and a curve has equation y=x 2
−kx+2, where k is a constant. a) Find the set of values of k for which the line and curve meet at two distinet points. b) For cach of two particular values of k, the line is a tangent to the curve. Show that these two tangents meet on the x-axis. 11. The equation x 2
+px+q=0, where p and q are constants, has roots −3 and 5 . a) Find the values of p and q. b) Using these values of p and q, find the value of the constant r for which the equation x 2
+px+q+r=0 has equal roots. 12. A curve has equation y=x 2
−4x+4 and a line has the equation y=mx, where m is a constant. a) For the case where m=1, the curve and the line intersect at the point A and B. b) Find the coordinates of the mid-point of AB. c) Find the non-zero value of m for which the line is the tangent to the curve, and find the coordinates of the point where the tangent touches the curve. Answer: 1. ( 2
1
,0) 9. a) 25−(x−5) 2
2. a) (3x− 2
5
) 2
− 4
25
b) (5,25) b) − 3
1
3
10. a) k>1,k<− 2
1
Answers
a) The set of values of k for which the line and curve meet at two distinct points is k < -2/5 or k > 2.
To find the set of values of k for which the line and curve meet at two distinct points, we need to solve the equation:
x^2 - kx + 2 = 3kx - 2k
Rearranging, we get:
x^2 - (3k + k)x + 2k + 2 = 0
For the line and curve to meet at two distinct points, this equation must have two distinct real roots. This means that the discriminant of the quadratic equation must be greater than zero:
(3k + k)^2 - 4(2k + 2) > 0
Simplifying, we get:
5k^2 - 8k - 8 > 0
Using the quadratic formula, we can find the roots of this inequality:
\(k < (-(-8) - \sqrt{((-8)^2 - 4(5)(-8)))} / (2(5)) = -2/5\\ or\\ k > (-(-8)) + \sqrt{((-8)^2 - 4(5)(-8)))} / (2(5)) = 2\)
Therefore, the set of values of k for which the line and curve meet at two distinct points is k < -2/5 or k > 2.
b) To find the two values of k for which the line is a tangent to the curve, we need to find the values of k for which the line is parallel to the tangent to the curve at the point of intersection. For m to be the slope of the tangent at the point of intersection, we need to have:
2x - 4 = m
3k = m
Substituting the first equation into the second, we get:
3k = 2x - 4
Solving for x, we get:
x = (3/2)k + (2/3)
Substituting this value of x into the equation of the curve, we get:
y = ((3/2)k + (2/3))^2 - k((3/2)k + (2/3)) + 2
Simplifying, we get:
y = (9/4)k^2 + (8/9) - (5/3)k
For this equation to have a double root, the discriminant must be zero:
(-5/3)^2 - 4(9/4)(8/9) = 0
Simplifying, we get:
25/9 - 8/3 = 0
Therefore, the constant term is 8/3. Solving for k, we get:
(9/4)k^2 - (5/3)k + 8/3 = 0
Using the quadratic formula, we get:
\(k = (-(-5/3) ± \sqrt{((-5/3)^2 - 4(9/4)(8/3)))} / (2(9/4)) = -1/3 \\or \\k= 4/3\)
Therefore, the two values of k for which the line is a tangent to the curve are k = -1/3 and k = 4/3. To show that the two tangents meet on the x-axis, we can find the x-coordinate of the point of intersection:
For k = -1/3, the x-coordinate is x = (3/2)(-1/3) + (2/3) = 1
For k = 4/3, the x-coordinate is x = (3/2)(4/3) + (2/3) = 3
Therefore, the two tangents meet on the x-axis at x = 2.
Learn more about " line and curve" : https://brainly.com/question/30162650
#SPJ11
In a sample of 28 participants, suppose we conduct an analysis of regression with one predictor variable. If Fobt= 4.28, then what is the decision for this test at a .05 level of significance?A) X significantly predicts Y.
B) X does not significantly predict Y.
C) There is not enough information to answer this question.
Answers
In a sample of 28 participants, suppose we conduct an analysis of regression with one predictor variable. If Fobt= 4.28, then the decision for this test at a .05 level of significance is there is not enough information to answer this question, option C.
To determine the decision for a regression analysis with one predictor variable at a 0.05 level of significance, we need to compare the observed F-statistic (Fobt) with the critical F-value.
Since the degrees of freedom for the numerator is 1 and the degrees of freedom for the denominator is 26 (28 participants - 2 parameters estimated), we can find the critical F-value from the F-distribution table or using statistical software.
Let's assume that the critical F-value at a 0.05 level of significance for this test is Fcrit.
If Fobt > Fcrit, then we reject the null hypothesis and conclude that X significantly predicts Y.
If Fobt ≤ Fcrit, then we fail to reject the null hypothesis and conclude that X does not significantly predict Y.
Since the information about the critical F-value is not provided, we cannot determine the decision for this test at a 0.05 level of significance. Therefore, the correct answer is C) There is not enough information to answer this question.
To learn more about variable: https://brainly.com/question/28248724
#SPJ11
Find the quotient of 1x10^-2 and 8x10^-2
Answers
Answer:
The first one is - 5 and the other is - 40
2 2.1 Mathematical intro show that there is another form for spherical harmonics: 1 3 3 Y₁ x iy 1/√√2 (²-1) 2πT 2π 1 3 3 z YO 2 2π π r 1 3 x iy Y₁¹ 3 2π - - 12 √ √ 2² (²+²) 2 2π
Answers
Spherical harmonics are an integral part of quantum mechanics. They describe the shape of the orbitals, which electrons occupy in atoms. Moreover, the spherical harmonics provide the angular distribution of a wave in spherical coordinates. In 3D, the spherical harmonics can be written as:
Ylm(θ, φ) = √(2l + 1)/(4π) * √[(l - m)!/(l + m)!] * Plm(cosθ) * e^(imφ)
Here, l and m are known as the angular quantum numbers. They define the shape and orientation of the orbital. Plm(cosθ) represents the associated Legendre polynomial, and e^(imφ) is the exponential function. The spherical harmonics have various forms, including:
Y1,1 = -Y1,-1 = 1/2 √(3/2π) sinθe^(iφ)
Y1,0 = 1/2 √(3/π)cosθ
Y2,2 = 1/4 √(15/2π)sin²θe^(2iφ)
Y2,1 = -Y2,-1 = 1/2 √(15/2π)sinθcosφ
Y2,0 = 1/4 √(5/π)(3cos²θ-1)
Y0,0 = 1/√(4π)
The spherical harmonics have various applications in physics, including quantum mechanics, electrodynamics, and acoustics. They play a crucial role in understanding the symmetry of various systems. Hence, the spherical harmonics are an essential mathematical tool in modern physics. Thus, this is how one can show another form for spherical harmonics.
To know more about Spherical harmonics visit
https://brainly.com/question/23067012
#SPJ11
Graph the function f(x)=
–
x2.
Answers
Answer:
f(x) = -x^2 is a downward parabola.
Step-by-step explanation:
The f(x) = x^2 graph is a parabola pointing up. Therefore, f(x) = -x^2 is a downward parabola.

Write the equation of the line in point-slope form:
(-8, 2) (-6, 8)
Answers
The equation of the line in point-slope form is:
y - 8 = 3(x + 6) or y - 2 = 3(x + 8).
What is the Equation of a Line in Point-Slope Form?The equation, y - b = m(x - a), represents the equation of a line in point-slope form, where:
(a, b) is a point on the linem is the slope of the line.Given two points, (-8, 2) and (-6, 8), find the slope (m) of the line that passes through the two points:
Slope (m) = change in y / change in x = (8 - 2)/(-6 -(-8))
Slope (m) = 6/2
Slope (m) = 3
Substitute m = 3 and (-6, 8) into y - b = m(x - a):
y - 8 = 3(x - (-6))
y - 8 = 3(x + 6)
Or substitute m = 3 and (-8, 2) into y - b = m(x - a):
y - 2 = 3(x - (-8))
y - 2 = 3(x + 8)
Therefore, the equation of the line in point-slope form is:
y - 8 = 3(x + 6) or y - 2 = 3(x + 8).
Learn more about point-slope form on:
https://brainly.com/question/24907633
#SPJ1
Taking a discount of 50% off followed by a discount of 50% off results in a total discount of _____. a. 25% b. 50% c. 75% d. 100%
Answers
Answer: 75% off the original price.
Step-by-step explanation:Say an item is $100. 50% off $100 is of coarse $50.
Now 50% off that price is $25.
So the new price is now $25 which is 75% off.
Answer:
c. 75%
Step-by-step explanation:
just took the test
brainliest pls?
HELPPPPPPPPPPPPPPPPP

Answers
Answer:
1/2 + 1/3 = 3/6 + 2/6 = 5/6
5/6 roughly equals to 0.8
The answer is C
Which of the following best estmates the sum: 1/2 + 1/3
Answer: C) 0.8
A model that describes the population of a fishery in whichharvesting takes place at a constant rate is given by (dP/dt) = kP- h,
where k and h are positive constants.
(a). Solve the DE subject to P(0) = P0.
(b). Describe the behavior of the population P(t) forincreasing time in three cases P0>h/k, P0=h/k, and0
(c). Use the results from part (b) to determine whether thefish population will ever go extinct in finite time, that is,whether there exists a time T>0 such that P(t) = 0. If thepopulation goes extinct, then find T
Answers
Based on the differential equation a) Solving the DE subject to P(0) = P0 will yield P = ((kP0 - h)e^(kt) + h)/k. b) For the three cases given (P0 > h/k, P0 = h/k, P0 = 0), the behavior of the population P(t) is will be population will grow without bound, the population will remain constant, and the population will decrease and approach zero as t approaches infinity respectively. c) The fish population will go extinct in finite time if there exists a time T > 0 such that P(T) = 0. At T = (1/k)ln(-h/(kP0 - h)) the fish population will go extinct.
(a) To solve the differential equation (dP/dt) = kP - h subject to P(0) = P0, we need to separate the variables and integrate both sides:
(dP/dt) = kP - h
dP/(kP - h) = dt
∫dP/(kP - h) = ∫dt
ln|kP - h| = kt + C
kP - h = e^(kt + C)
P = (e^(kt + C) + h)/k
Using the initial condition P(0) = P0, we can solve for C:
P0 = (e^(k*0 + C) + h)/k
P0 = (e^C + h)/k
e^C = kP0 - h
C = ln(kP0 - h)
Substituting back into the equation for P, we get:
P = (e^(kt + ln(kP0 - h)) + h)/k
P = ((kP0 - h)e^(kt) + h)/k
This is the solution to the differential equation subject to the initial condition P(0) = P0.
(b) The behavior of the population P(t) for increasing time depends on the initial condition P0:
- If P0 > h/k, then the term (kP0 - h)e^(kt) will be positive and will increase exponentially as t increases, so the population will grow without bound.
- If P0 = h/k, then the term (kP0 - h)e^(kt) will be zero and the population will remain constant at P = h/k for all time.
- If P0 < h/k, then the term (kP0 - h)e^(kt) will be negative and will decrease exponentially as t increases, so the population will decrease and approach zero as t approaches infinity.
(c) The fish population will go extinct in finite time if there exists a time T > 0 such that P(T) = 0. From the equation for P, we can see that this will happen if and only if P0 < h/k:
P(T) = ((kP0 - h)e^(kT) + h)/k = 0
(kP0 - h)e^(kT) = -h
e^(kT) = -h/(kP0 - h)
Since the exponential function is always positive, this equation has no solution for P0 > h/k or P0 = h/k. However, if P0 < h/k, then the term (kP0 - h) is negative and the equation has a solution:
kT = ln(-h/(kP0 - h))
T = (1/k)ln(-h/(kP0 - h))
This is the time at which the fish population will go extinct.
Learn more about Differential equation:
https://brainly.com/question/1164377
#SPJ11
Please answer with some work shown!
- Kirstin is decorating her bedroom wall with photographs.
She has 36 photographs of family and 28 photographs of friends.
She wants to arrange the photographs in rows so that each row
has the same number of photographs, and photographs of family
and photographs of friends do not appear in the same row.
a. How many rows will there be if Kirstin puts the greatest possible
number of photographs in each row?
b. How many photographs will be in each row?
Answers
Answer:
there will be 8 rows
the number of photographs in each row is 8
Ira enters a competition to guess how many buttons are in a jar. Ira’s guess is 200 buttons. The actual number of buttons is 250. What is the percent error of Ira’s guess?.
Answers
Using the percent error formula
200-250=-50
-50/250= -0.2
-0.2x100=-20
Help me ?? Please I’m stuck
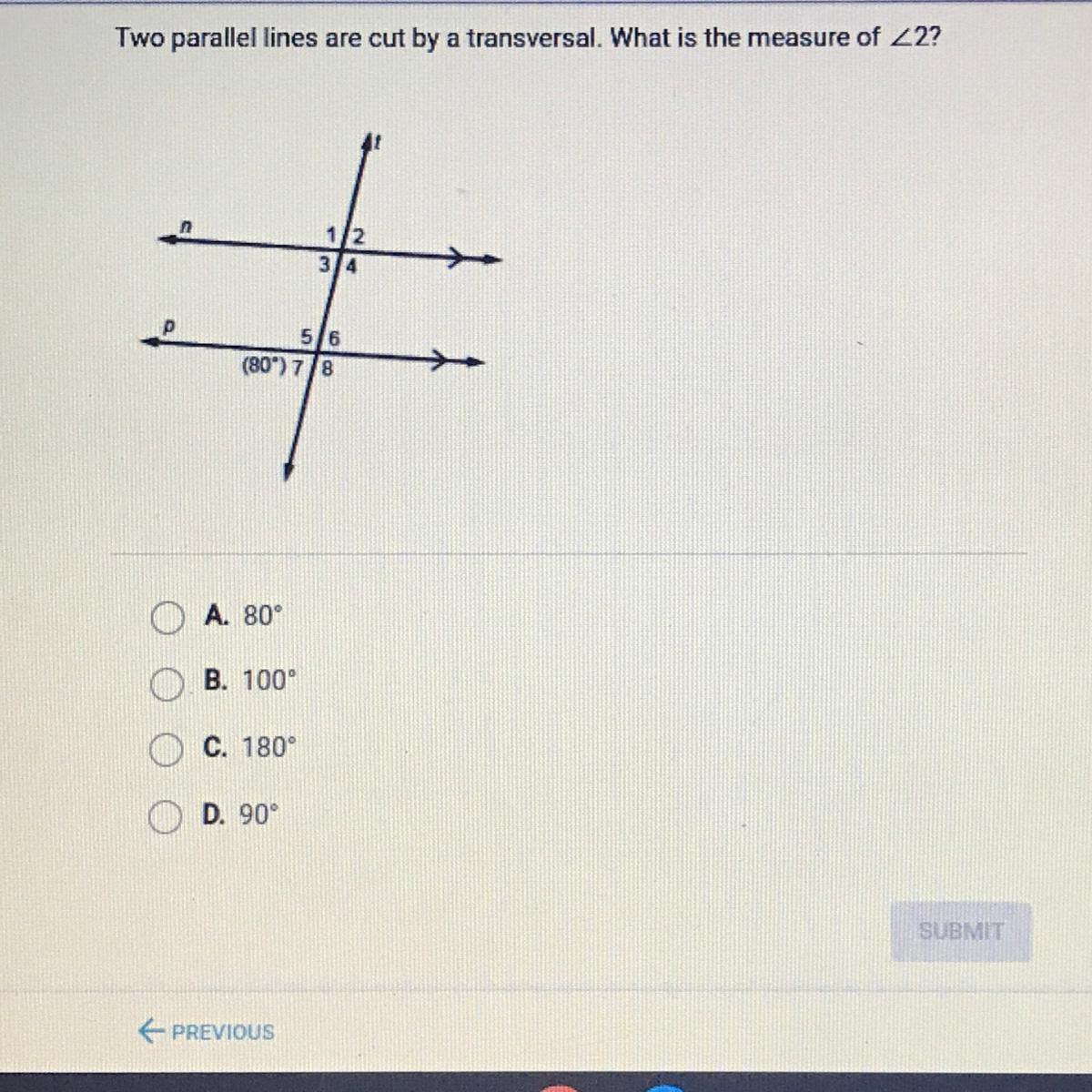
Answers
Answer:
A. 80
Step-by-step explanation:
2 is corresponding to 6 and 6 is vertical with 7. Making them all congruent. And since we know 7 is 80 degrees then there is your answer. Hope that helped :))
Help me with this question i don’t understand what to do

Answers
Answer:
- 36
Step-by-step explanation:
First evaluate g(18), then substitute the value obtained into h(x), then substitute the value obtained here into f(x).
g(18) = \(\sqrt{2(18)}\) = \(\sqrt{36}\) = 6, then
h(6) = | 4(6) | - 12 = | 24 | - 12 = 24 - 12 = 12, then
f(12) = - 3(12) = - 36
.8 Convert 23.4587{ha}+0: a) Square survey feet b) acres c) Square Gunter's Chains
Answers
23.4587 hectares is equal to 2,529,708.3512 square survey feet. 23.4587 hectares is equal to 57.9965 acres. 23.4587 hectares is equal to 0.9272 square Gunter's Chains.
Given: 23.4587 ha
To convert 23.4587 hectares to square survey feet, acres and square Gunter's Chains Conversions:
1 Hectare = 107639.1041671 Square Survey Feet
1 Hectare = 2.47105381 Acres
1 Hectare = 0.0395369 Square Gunter's Chains
To convert 23.4587 hectares to square survey feet, multiply by the conversion factor.
23.4587 ha × 107639.1041671 square survey feet/ha = 2529708.3512 square survey feet
Therefore, 23.4587 hectares is equal to 2,529,708.3512 square survey feet.
To convert 23.4587 hectares to acres, multiply by the conversion factor.
23.4587 ha × 2.47105381 acres/ha = 57.9965 acres
Therefore, 23.4587 hectares is equal to 57.9965 acres.
To convert 23.4587 hectares to square Gunter's Chains, multiply by the conversion factor.
23.4587 ha × 0.0395369 square Gunter's Chains/ha = 0.9272 square Gunter's Chains
Therefore, 23.4587 hectares is equal to 0.9272 square Gunter's Chains.
Learn more about Gunter's Chains visit:
brainly.com/question/30408280
#SPJ11
Suppose an insurance company wants to determine the average speed of cars passing through an intersection. They randomly selected 85 cars and found their average speed to be 42 miles per hour with standard deviation of 4.2 miles per hour. A 90% confidence interval for the average speed of all the cars passing through the intersection is
Answers
The 90% confidence interval for the average speed of all the cars passing through the intersection is (41.29, 42.71) miles per hour.
To calculate the confidence interval, we can use the formula:
Confidence interval = Sample mean ± (Critical value * Standard error)
Given that the sample mean is 42 miles per hour and the standard deviation is 4.2 miles per hour, we need to determine the critical value and the standard error.
Since we have a sample size of 85, we can use the t-distribution with (n-1) degrees of freedom to find the critical value. With a 90% confidence level, the corresponding critical value for a two-tailed test is approximately 1.66.
The standard error is calculated as the standard deviation divided by the square root of the sample size:
Standard error = (Standard deviation) / √(Sample size)
Standard error = 4.2 / √85 ≈ 0.456
Now we can plug in the values into the confidence interval formula:
Confidence interval = 42 ± (1.66 * 0.456)
Confidence interval ≈ (41.29, 42.71)
Therefore, the 90% confidence interval for the average speed of all the cars passing through the intersection is (41.29, 42.71) miles per hour.
Based on the given data and calculations, we can conclude that with 90% confidence, the average speed of all the cars passing through the intersection falls within the range of 41.29 to 42.71 miles per hour.
To know more about intersection , visit :
https://brainly.com/question/12089275
#SPJ11