estimate 54.68 +93 (please explain in number form as possible)
Answers
Answer:90+55=145
Step-by-step explanation:
54.68+93 is about 55+90 or 55+100
55+100=155
90+55=145
54.68+93=147.68
Related Questions
Hello, I am currently very stuck with this problem and I am unsure as to how I would solve it.

Answers
We have the equation
\(20y=x^2-10-15\)Let's complete the square, to do it let's add and subtract 25 on the right side
\(\begin{gathered} 20y=x^2-10-15+25-25 \\ \\ 20y=(x-5)^2-15-25_{} \\ \\ 20y=(x-5)^2-40 \\ \\ \end{gathered}\)Now we can have y in function of x
\(\begin{gathered} y=\frac{1}{20}(x-5)^2-2 \\ \\ \end{gathered}\)Now we can already identify the vertex because it's in the vertex form:
\(y=a(x-h)+k\)Where the vertex is
\((h,k)\)As we can see, h = 5 and k = -2, then the vertex is
\((5,-2)\)Now we can continue and find the focus, the focus is
\(\mleft(h,k+\frac{1}{4a}\mright)\)We have a = 1/20, therefore
\(\begin{gathered} \mleft(5,-2+5\mright) \\ \\ (5,3) \end{gathered}\)The focus is
\((5,3)\)And the last one, the directrix, it's
\(y=k-\frac{1}{4a}\)Then
\(\begin{gathered} y=-2-5 \\ \\ y=-7 \end{gathered}\)Hence the correct answer is: vertex (5, -2); focus (5, 3); directrix y = -7
plss help me do this giving brainliest

Answers
Answer:
Step-by-step explanation:
A right triangle has a right angle in it. The base and height are then the sides that make the right angle. You can change the 2.5 to a fraction 5/2 or leave it a decimal and just use your calculator. Once the base and height are drawn, you don't have to calculate the hypotenuse (the longest side) just connect the third side. See image. Also, def do this on graph paper it's easier. The new triangle should be bigger than the original this time bc 2.5 is bigger than 1 and so it makes your shape bigger.

How do you solve question 1
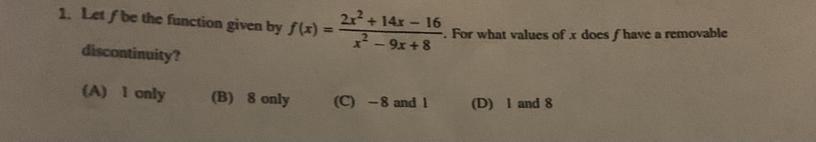
Answers
9514 1404 393
Answer:
(A) 1 only
Step-by-step explanation:
Factor numerator and denominator and see what cancels.
\(f(x)=\dfrac{2x^2+14x-16}{x^2-9x+8}=\dfrac{2(x-1)(x+8)}{(x-1)(x-8)}=\dfrac{x-1}{x-1}\cdot\dfrac{2(x+8)}{x-8}\\\\f(x)=\dfrac{2x+16}{x-8}\qquad x\ne1\)
The factor of x-1 in the original denominator means the expression is undefined at x=1. The reduced expression is defined there, so the discontinuity at x=1 could be removed by defining f(1) = -18/7.
There is a removable discontinuity at x=1 only. The discontinuity at x=8 is a vertical asymptote where the function changes sign. It cannot be removed by defining a value for the function there.
Which of these statements is true?

Answers
Answer: WX, ZY and WX and AB.
The 2nd one is correct.
Decide whether or not it is a function.

Answers
The table shows the greatest distance, In yards, that Bruce hit with six different clubs. State these distances in feet. The ratio of yards to feet Is 1: 3.
Answers
The answer for distance I will be explaining nothing else I’ll just say the distance of feet
The nine iron is 297 distance the 7-iron is 360 the 5 iron is 432 the 3 iron is 486 the 3 wood is 522 and the Driver is 576
how many miles could he ride in 3 hr

Answers
In case whereby Jake rides his bicycle 6 miles in 3/5 of an hour. At this rate, the number of miles could he ride in 3 hours is 30 miles
How can the number of miles be calculated?The distance = bicycle 6 miles
number of hours =3/5 of an hour
then the rate = 6/ (3/5)
Then we can calculate the number of miles with the 6milesi n 3/5 hours as;
= (6 * 5/3 )
=30/3
=10
Then the rate will be 10 miles in 1 hour , hence the number of miles he will ride in 3hrs
=10 * 3 hours
= 30 miles
Learn more about miles at:
https://brainly.com/question/29806974
#SPJ1
Find the open intervals on which the function f(x)= x+10sqrt(9-x) is increasing or decreasing.

Answers
The function f(x) = x + 10√(9 - x) is increasing on the interval (-∞, 9) and decreasing on the interval (9, ∞).
To determine the intervals on which the function is increasing or decreasing, we need to find the derivative of the function and analyze its sign.
Let's find the derivative of the function f(x) = x + 10√(9 - x) with respect to x.
f'(x) = 1 + 10 * (1/2) * (9 - x)^(-1/2) * (-1)
= 1 - 5√(9 - x) / √(9 - x)
= 1 - 5 / √(9 - x).
To analyze the sign of the derivative, we need to find the critical points where the derivative is equal to zero or undefined.
Setting f'(x) = 0:
1 - 5 / √(9 - x) = 0
5 / √(9 - x) = 1
(√(9 - x))^2 = 5^2
9 - x = 25
x = 9 - 25
x = -16.
The critical point is x = -16.
We can see that the derivative f'(x) is defined for all x values except x = 9, where the function is not differentiable due to the square root term.
Now, let's analyze the sign of the derivative f'(x) in the intervals (-∞, -16), (-16, 9), and (9, ∞).
For x < -16:
Plugging in a test value, let's say x = -17, into the derivative:
f'(-17) = 1 - 5 / √(9 - (-17))
= 1 - 5 / √(9 + 17)
= 1 - 5 / √26
≈ 1 - 0.97
≈ 0.03.
Since f'(-17) is positive, the function is increasing in the interval (-∞, -16).
For -16 < x < 9:
Plugging in a test value, let's say x = 0, into the derivative:
f'(0) = 1 - 5 / √(9 - 0)
= 1 - 5 / √9
= 1 - 5 / 3
≈ 1 - 1.67
≈ -0.67.
Since f'(0) is negative, the function is decreasing in the interval (-16, 9).
For x > 9:
Plugging in a test value, let's say x = 10, into the derivative:
f'(10) = 1 - 5 / √(9 - 10)
= 1 - 5 / √(-1)
= 1 - 5i,
where i is the imaginary unit.
Since the derivative is not a real number for x > 9, we cannot determine the sign.
Combining the information, we conclude that the function f(x) = x + 10√(9 - x) is increasing on the interval (-∞, 9) and decreasing on the interval (9, ∞).
For more such questions on function, click on:
https://brainly.com/question/11624077
#SPJ8
Zero(s) of multiplicity one:
Zero(s) of multiplicity two:
Zero(s) of multiplicity three:
Please look at photo for the full question. Thank you.

Answers
The zeros and the multiplicities are
Zero(s) of multiplicity one: x = 6Zero(s) of multiplicity two: x = 11Zero(s) of multiplicity three: x = -6 and x = -5How to determine the zeros and the multiplicitiesfrom the question, we have the following parameters that can be used in our computation:
f(x) = (x + 6)³(x - 11)²(x - 6)(x + 5)³
The power of each factor are the multiplicities
So, we have
Zero(s) of multiplicity one:
x - 6 = 0
Zero(s) of multiplicity two:
x - 11 = 0
Zero(s) of multiplicity three:
x + 6 = 0 and x + 5 = 0
When evaluated, we have
Zero(s) of multiplicity one:
x = 6
Zero(s) of multiplicity two:
x = 11
Zero(s) of multiplicity three:
x = -6 and x = -5
Read more about polynomial at
https://brainly.com/question/30833611
#SPJ1
The base of a hexagonal pyramid has an area of 92 square inches. The height of the pyramid is 6 inches. Find the volume of the pyramid.
Answers
The volume of the hexagonal pyramid is 508.93 cubic inches.
The formula for the volume of a pyramid is:
Volume = (1/3) x base area x height
In this case, we are given that the base of the pyramid is a regular hexagon with an area of 92 square inches, and the height is 6 inches.
To find the volume of the pyramid, we need to first find the area of one of the triangles that make up the hexagonal base. Each of the six triangles in the base is an equilateral triangle, so we can use the formula for the area of an equilateral triangle to find the area of one of the triangles:
Area of an equilateral triangle = (\(\sqrt{3}\)/4) x \((side)^{2}\)
Since the base of the pyramid is a regular hexagon, all six sides are equal. Let's call the length of one side "s". Then we have:
Area of one triangle = (\(\sqrt{3}\)/4) x \(s^{2}\)
To find the total area of the hexagonal base, we can multiply the area of one triangle by the number of triangles in the base:
Area of hexagonal base = 6 x(\(\sqrt{3}\)/4) x \(s^{2}\)
We are given that the area of the hexagonal base is 92 square inches, so we can solve for "s":
6 x (\(\sqrt{3}\)/4) x \(s^{2}\) = 92
(\(\sqrt{3}\)/4) x \(s^{2}\) = 92/6
\(\sqrt{3}\) x \(s^{2}\) = 46
\(s^{2}\) = 46/\(\sqrt{3}\)
s ≈ 6.21 inches
Now that we know the length of one side of the hexagonal base, we can find the area of the base by using the formula for the area of a regular hexagon:
Area of hexagonal base = (3\(\sqrt{3}\) /2) x \(s^{2}\)
Area of hexagonal base ≈ 254.47 square inches
Finally, we can use the formula for the volume of a pyramid to find the volume of the hexagonal pyramid:
Volume = (1/3) x base area x height
Volume = (1/3) x 254.47 x 6
Volume ≈ 508.93 cubic inches
To learn more about hexagonal pyramid here:
https://brainly.com/question/29713978
#SPJ4
What is the value of r

Answers
Step-by-step explanation:
Vertical angles are equal r = 70 degrees
Francium is an element with a half-life of 22 minutes. 1000 grams of francium is placed into a bowl determine how much Francium (in grams) will be left after 2 hours

Answers
The amount of the element, Francium, that will remain after 2 hours is 31.25 grams.
Half-life problemTo determine how much francium will be left after 2 hours, we need to calculate the number of half-lives that occur within that time period.
Given that the half-life of francium is 22 minutes, we can calculate the number of half-lives in 2 hours (120 minutes):
Number of half-lives = (Total time elapsed) / (Half-life)
Number of half-lives = 120 minutes / 22 minutes ≈ 5.4545
Since we can't have a fraction of a half-life, we take the integer part, which is 5.
Each half-life represents a halving of the amount of francium. So, after 5 half-lives, the remaining amount of francium can be calculated using the formula:
Remaining amount = Initial amount * (1/2)^(Number of half-lives)
Given that the initial amount is 1000 grams, we can calculate the remaining amount after 2 hours:
Remaining amount = 1000 grams * \((1/2)^5\)
Remaining amount ≈ 1000 grams * 0.03125
Remaining amount ≈ 31.25 grams
Therefore, after 2 hours, approximately 31.25 grams of francium will be left.
More on half-life can be found here: https://brainly.com/question/31666695
#SPJ1
Find the value of z.
X
7
Y
3
Z
Z = √[?]
![Find the value of z.X7Y3 Z Z = [?]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/lyH462HEzMZ5f6EQv6R7ScwGpUBNizoY.png)
Answers
Answer:
z = \(\sqrt{30}\)
Step-by-step explanation:
using the Altitude- on- Hypotenuse theorem
(leg of big Δ )² = (part of hypotenuse below it ) × (whole hypotenuse)
z² = 3 × (3 + 7) = 3 × 10 = 30 ( take square root of both sides )
z = \(\sqrt{30}\)
What is the first error Zoe made in her proof?
a. Zoe used an invalid reason to justify the congruence of a pair of sides or angles
b. Zoe only established some of the necessary conditions for a congruence criterion.
c. Zoe established all necessary conditions, but then used an inappropriate congruence criterion.
d. Zoe used a criterion that does not guarantee congruence
iui
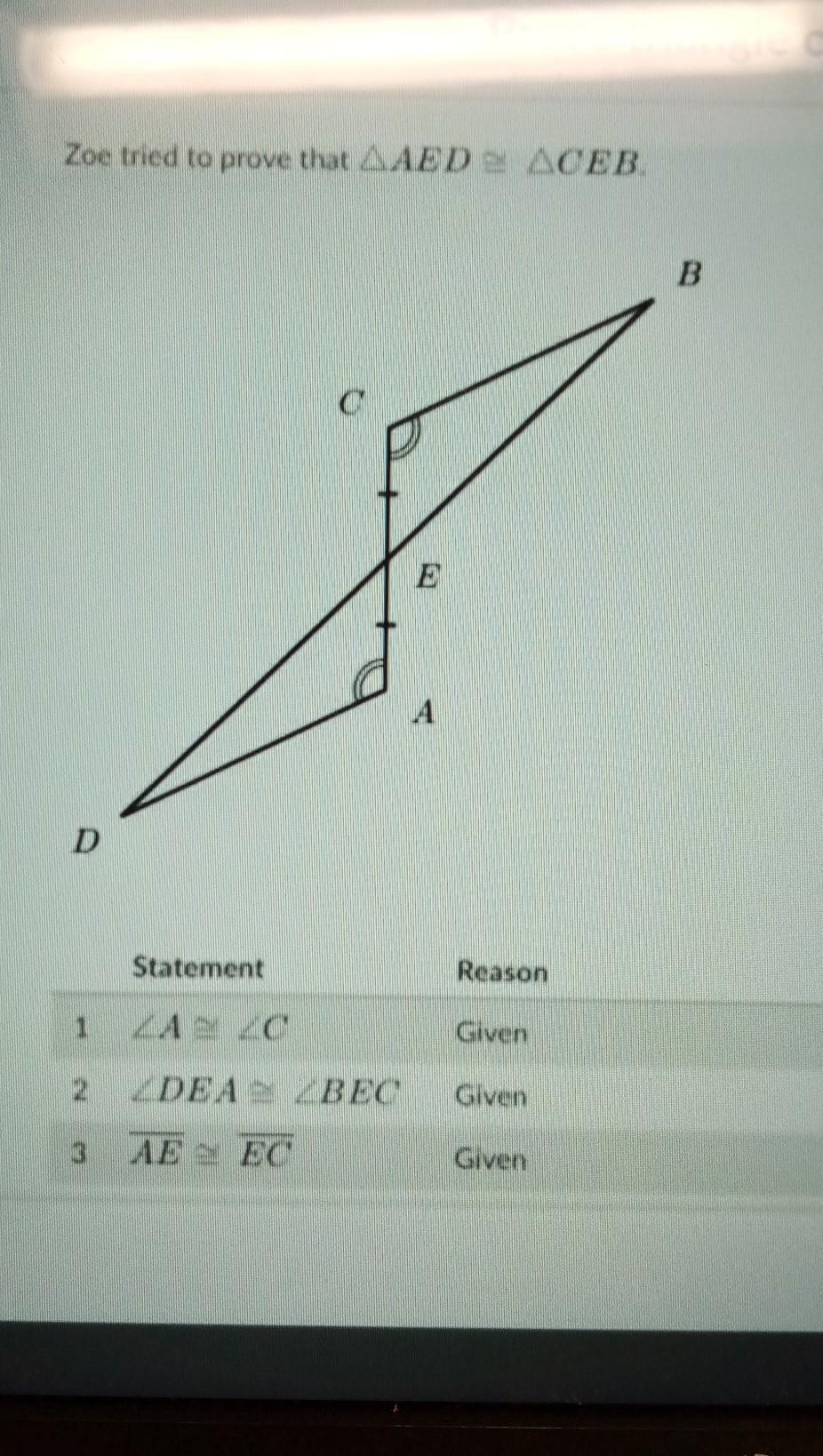
Answers
Answer:
a
Step-by-step explanation:
To prove congruence
1 ∠ A ≅ ∠ C → given
2 ∠ DEA ≅ ∠ BEC → vertically opposite angles
3. AE ≅ EC → given
We then have 2 angles and the included side ( side between the 2 angles )
congruent in both triangles, thus Δ AED ≅ Δ CEB ( ASA postulate )
Zoes' error was in assuming ∠ DEA ≅ ∠ BEC was given
Zoe used an invalid reason to justify the congruence of a pair of sides or angles.
Option a is correct.
From given diagram it is observed that,
Line segment AD and CB are parallel and AC is transversal line. So that alternate angles A and C are equal.
\(\angle A=\angle C\)
When two lines intersect at any point then vertically opposite angles are equal.
So that, \(\angle DEA=\angle BEC\)
Given that , \(AE=EC\)
The Angle-Side-Angle Postulate (ASA) states that if two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the two triangles are congruent.
Hence, both triangles are congruent to each other.
Learn more:
https://brainly.com/question/25920974
Test the claim below about the mean of the differences for a population of paired data at the level of significance α Assume the samples are random and dependent, and the populations are normally distributed Claim μ,-0: α-0.10. Sample statistics: d-3.5, sd-894, n-9 Identify the null and alternative hypotheses. Choose the correct answer below The test statistic is t (Round to two decimal places as needed) The critical value(s) is(are)- (Round to two decimal places as needed. Use a comma to separate answers as needed.) Since the test statistic isthe rejection region, the null hypothesis. There statistically significant evidence to reject the claim.
Answers
Complete Question
The complete question is shown on the first uploaded image
Answer:
The correct option is F
\(t = 1.17\)
\(t_ {\alpha , df} =t_ {0.10 , 8} = 1.86\)
Since the test statistics is outside the rejection region , we fail to reject the null hypothesis ,There is no statistically significant evidence to reject the claim
Step-by-step explanation:
From the question we are told that
The claim is \(\mu = 0\)
Hence
The null hypothesis is \(H_o : \mu = 0\)
The alternative is \(H_a : \mu \ne 0\)
Generally the test statistics is mathematically represented as
\(t = \frac{\= d - \mu_d }{ \frac{s_d}{ \sqrt{n} } }\)
=> \(t = \frac{3.5 -0 }{ \frac{8.94}{ \sqrt{9} } }\)
=> \(t = 1.17\)
Generally the degree of freedom is mathematically represented as
\(df = n- 1\)
\(df = 9 - 1\)
\(df = 8\)
From the student t-distribution table the critical value of \(\alpha\) at a degree of freedom of 8 is
\(t_ {\alpha , df} =t_ {0.10 , 8} = 1.86\)
Since the \(t_ {\alpha , df}\) is outside the rejection region , we fail to reject the null hypothesis ,There is no sufficient evidence to reject the claim

Which point lies on the y-axis?

Answers
Answer:
(0,2)
Step-by-step explanation:
Heather solved this problem:
75 is 300% of what number?
A tape diagram. StartFraction part Over whole EndFraction = StartFraction 300 Over 100 EndFraction = StartFraction 75 Over question mark EndFraction. StartFraction part Over whole EndFraction = StartFraction 75 times 4 Over 100 times 4 EndFraction = StartFraction 300 Over 400 EndFraction
What error did Heather make?
None. Her work is correct.
She multiplied 75 and 4 incorrectly.
She should have divided 75 by 4, and divided 100 by 4.
She used the part, 75, to write the percent ratio. The part-to-whole percent ratio is StartFraction 300 Over 100 EndFraction
Answers
Answer:
A tape diagram. StartFraction part Over whole EndFraction = StartFraction 300 Over 100 EndFraction = StartFraction 75
Step-by-step explanation:
Answer: (D)
Start Learning and Start Growing! edge2023!
*DROPS THE MIC*

Tickets for the school play sell for $4 each. Which graph shows the relationship between the number of tickets solo
(x) and the total income from the tickets (y)?

Answers
Answer:
I do not see all the graphs but it would be the reverse of what is shown for A. graph. The tickets sold to total income would have to be a 1:4 ratio where every 4 dollar leap in the y-axis is a one point (1 unit change in x).
Step-by-step explanation:
Isabella tossed a coin and spun a spinner that is divided into 3 equal sections. She did this 50 times. The results are shown in the table. What is the experimental probability that the next time Isabella tosses the coin and spins the spinner she will get a tails and a 2? *
Answers
Answer:
ur gay landen
Step-by-step explanation:
Limit x approaches 0 (tan^2x-sin) divide by x4

Answers
\(\displaystyle \lim_{\theta \to 0}\cfrac{\tan^2(\theta )-\sin(\theta )}{\theta 4}\implies \stackrel{\textit{\Large L'Hopital's rule}}{\lim_{\theta \to 0}\cfrac{\frac{d}{d\theta }[\tan^2(\theta )-\sin(\theta )]}{\frac{d}{d\theta }[\theta 4]}} \\\\[-0.35em] ~\dotfill\)
\(\cfrac{d}{d\theta }[\tan^2(\theta )-\sin(\theta )]\implies \cfrac{d}{d\theta }[[\tan(\theta )]^2-\sin(\theta )]\implies \stackrel{chain~rule}{2\tan(\theta )\cdot \sec^2(\theta )} ~~ -\cos(\theta ) \\\\\\ 2\tan(\theta )\cdot \cfrac{1}{\cos^2(\theta )}-\cos(\theta )\implies \cfrac{~~ \frac{2\sin(\theta) }{\cos(\theta) } ~~}{\cos^2(\theta )}~~ -\cos(\theta ) \\\\\\ \cfrac{2\sin(\theta) }{\cos^3(\theta) }~~ -\cos(\theta )\implies \cfrac{2\sin(\theta)-\cos^4(\theta)}{\cos^3(\theta)} \\\\[-0.35em] ~\dotfill\)
\(\cfrac{d}{d\theta}[4\theta]\implies 4 \\\\[-0.35em] ~\dotfill\)
\(\displaystyle \lim_{\theta \to 0}\cfrac{\tan^2(\theta )-\sin(\theta )}{\theta 4}\implies \lim_{\theta \to 0}\cfrac{ ~~ \frac{2\sin(\theta)-\cos^4(\theta)}{\cos^3(\theta)} ~~ }{4}\implies \lim_{\theta \to 0}\cfrac{2\sin(\theta)-\cos^4(\theta)}{4\cos^3(\theta)} \\\\\\ \displaystyle \lim_{\theta \to 0}\cfrac{2\sin(0)-\cos^4(0)}{4\cos^3(0)}\implies \lim_{\theta \to 0}\cfrac{2(0)-1^4}{4(1^3)}\implies {\Large \begin{array}{llll} -\cfrac{1}{4} \end{array}}\)
A scientist was tracking the diving patterns of whales. A whale was at a depth of 3 meters below sea level and then dove an amount of ten meters twice before ascending four meters. The scientist noted that the whale’s current depth in relation to sea level was -16 m. What error did the scientist make?
A The scientist used a negative amount when it should be positive. The correct answer is 16 m.
B The scientist did not include the whale’s starting depth. The correct answer is -19 m.
C The scientist needed to add all the amounts together. The correct answer is -27 m.
D The scientist did not make an error. The correct answer is -16 m.
Answers
Answer:
the answer is b
Step-by-step explanation:
i got the question correct with the answer b
4.8 is what percent of 12
Answers
Answer:
40%
Step-by-step explanation:
4.8 * 100 = 480
480 / 12 = 40
= 40%
I hope this helps.
Note: Enter your answer and show all the steps that you use to
solve this problem in the space provided.
You have a credit card with a balance of $1,367.90 at a 9.5%
APR. You pay $400.00 each month on the due date until the
card is paid off. How many months does it take to pay off the
card, and what is the total amount paid including interest?
Be sure to include in your response:
• the answer to the original question
. the mathematical steps for solving the problem
demonstrating mathematical reasoning
Answers
Given statement solution is :- It takes 4 months to pay off the card, and the total amount paid, including interest, is $1600.
To determine the number of months it takes to pay off the credit card and the total amount paid, including interest, we can follow these steps:
Step 1: Calculate the monthly interest rate.
The APR (Annual Percentage Rate) is given as 9.5%. To find the monthly interest rate, we divide this by 12 (the number of months in a year):
Monthly interest rate = 9.5% / 12 = 0.0079167
Step 2: Determine the monthly payment.
The monthly payment is given as $400.
Step 3: Calculate the interest and principal paid each month.
The interest paid each month can be calculated by multiplying the monthly interest rate by the current balance.
Principal paid = Monthly payment - Interest paid
Step 4: Track the remaining balance each month.
Starting with the initial balance of $1,367.90, subtract the principal paid each month to determine the new balance.
Step 5: Repeat Steps 3 and 4 until the balance reaches zero.
Continue calculating the interest and principal paid each month, updating the balance, until the remaining balance becomes zero.
Step 6: Determine the total number of months and the total amount paid.
Count the number of months it takes to reach a balance of zero. Multiply the number of months by the monthly payment ($400) to find the total amount paid.
Let's calculate the number of months and the total amount paid, including interest:
Month 1:
Interest paid = 0.0079167 * $1,367.90 = $10.84
Principal paid = $400 - $10.84 = $389.16
New balance = $1,367.90 - $389.16 = $978.74
Month 2:
Interest paid = 0.0079167 * $978.74 = $7.75
Principal paid = $400 - $7.75 = $392.25
New balance = $978.74 - $392.25 = $586.49
Month 3:
Interest paid = 0.0079167 * $586.49 = $4.64
Principal paid = $400 - $4.64 = $395.36
New balance = $586.49 - $395.36 = $191.13
Month 4:
Interest paid = 0.0079167 * $191.13 = $1.51
Principal paid = $400 - $1.51 = $398.49
New balance = $191.13 - $398.49 = -$207.36 (Paid off)
It takes 4 months to pay off the credit card. Now, let's calculate the total amount paid, including interest:
Total amount paid = 4 * $400 = $1600
Therefore, it takes 4 months to pay off the card, and the total amount paid, including interest, is $1600.
For such more questions on Credit Card Payoff
https://brainly.com/question/26867415
#SPJ8
Question:-
The area of two similar triangles are 81 cm2 and 49 cm² respectively. If one of the sides of the first triangle is 6.3 cm, find the corresponding side of the other triangle.
Answers
Let's assume that the corresponding side of the second triangle is \(\displaystyle\sf x\).
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides. Therefore, we can set up the following proportion:
\(\displaystyle\sf \left( \dfrac{x}{6.3} \right)^{2} =\dfrac{49}{81}\)
To find \(\displaystyle\sf x\), we can solve the proportion above:
\(\displaystyle\sf \left( \dfrac{x}{6.3} \right)^{2} =\dfrac{49}{81}\)
Taking the square root of both sides:
\(\displaystyle\sf \dfrac{x}{6.3} =\sqrt{\dfrac{49}{81}}\)
Simplifying the square root:
\(\displaystyle\sf \dfrac{x}{6.3} =\dfrac{7}{9}\)
Cross-multiplying:
\(\displaystyle\sf 9x = 6.3 \times 7\)
Dividing both sides by 9:
\(\displaystyle\sf x = \dfrac{6.3 \times 7}{9}\)
Calculating the value:
\(\displaystyle\sf x = 4.9\)
Therefore, the corresponding side of the second triangle is \(\displaystyle\sf 4.9 \, cm\).
\(\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}\)
♥️ \(\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}\)
Answer:
Step-by-step explanation:
let's assume that the corresponding side of the second triangle is .
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides. Therefore, we can set up the following proportion:
To find , we can solve the proportion above:
Taking the square root of both sides:
Simplifying the square root:
Cross-multiplying:
Dividing both sides by 9:
Calculating the value:
Therefore, the corresponding side of the second triangle is 4.9cm
hope it helped u dear...........
3. What is the product of 22.5 and 3.32?
A. 74.700
B. 747.00
C. 13.950
D. 139.50
Answers
Answer:
A
Step-by-step explanation:
22.5 times 3.32 results in 74.7, or A.
Janet is 33.3% finished with
her math homework. If she
has 24 questions, how many
does she have left to finish?
Answers
Solve for the missing side length. Round to the nearest tenth.
5.8
5.2
5.4
5.6

Answers
Answer:
C) 5.4-------------------------
Given two legs of a right triangle and we need to find the hypotenuse.
Use Pythagorean theorem:
\(PQ = \sqrt{QR^2+PR^2}\)\(PQ = \sqrt{2^2+5^2} =\sqrt{29} =5.385 = 5.4\ (rounded)\)The matching choice is C.
explain the types of frequency distribution in statistics
Answers
The two types of frequency distributions are Discrete Frequency Distribution and Grouped Frequency Distribution
What are the types of distribution?The two types of frequency distributions are;
Discrete Frequency Distribution:Grouped Frequency DistributionWhen the data consists of discrete, separate values, this sort of distribution is used. It displays the frequency or number of occurrences of each value.
The data is often expressed in a table with two columns: one for distinct values and another for the frequencies of those values.
This distribution is utilized when the data is continuous and has a wide range of values. It entails categorizing the data into intervals or classes and then calculating the frequency of values that fall within each interval.
Learn more about frequency distribution at: https://brainly.com/question/27820465
#SPJ1
5
4
3-
Mark this and return
N
-5-4-3-2-1₁.
24
1+
GAW N
y
+2+
-3
-4
1 2 3 4 5 x
What is the range of the function on the graph?
O all the real numbers
O
all the real numbers greater than or equal to 0
all the real numbers greater than or equal to 2
O all the real numbers greater than or equal to -3
Save and Frit
Answers
The range of the function on the graph would be: D. all real numbers greater than or equal to 2
How to calculate the function rangeTo obtain the range, observe the y values whose result can be obtained by the function of x. To obtain this range, we examine the graph and note that the range begins from 2 on the y-axis and extends upwards.
So, if we wish to define our range, we will enter all real numbers that are equal to or greater than 2 as seen in the direction of the graph.
Learn more about graphs here:
https://brainly.com/question/19040584
#SPJ1

THIS IS NOT MY WORK! Need help solving the problems to put on graph


Answers
The graph of the inequality -4 ≤ x - 5 < -1 is given by the image presented at the end of the answer.
How to graph the inequality?The inequality for this problem is defined as follows:
-4 ≤ x - 5 < -1
It is a compound inequality, hence the lower bound of the solution is obtained as follows:
x - 5 ≥ -4
x ≥ 1.
(closed border).
The upper bound of the solution is obtained as follows:
x - 5 < -1
x < 4.
(open border).
Then the solution is given as follows:
1 ≤ x < 4.
More can be learned about inequality at https://brainly.com/question/9774970
#SPJ1
