Erika is landscaping her front yard. The yard, which is
level, has the shape of a rectangle that is 60 feet wide
by 80 feet long. To cover the yard with a layer of
topsoil having a uniform depth of 4 inches (į foot),
Erika needs to use how many cubic feet of topsoil?
Answers
Erika would need 1,599.36 cubic feet of topsoil.
In order to determine the cubic feet of topsoil, the volume of the front yard has to be determined.
Volume = length x width x height
The dimensions of the depth has to converted to feet
1 inch= 0.0833 feet
4 inches x 0.0833 = 0.3332
Volume = 60 x 80 x 0.0332 = 1,599.36 cubic feet
To learn more, please check: https://brainly.com/question/3677954
Related Questions
2.35 × 10−3 in standard form?
Answers
Answer: 20.5
Step-by-step explanation:
the test statistic for testing equality of proportions multiple select question. assumes when samples are large that p1 - p2 is normally distributed. uses a pooled proportion to calculate the standard error. is a t statistic. is a z score
Answers
The test statistic for testing equality of proportions is a z-score. It is calculated by dividing the difference in sample proportions by the standard error. The resulting z-score is then compared to critical values from the standard normal distribution to determine the statistical significance of the difference in proportions.
The correct options for the test statistic for testing the equality of proportions in a multiple-select question are:
Assumes when samples are large that p1 - p2 is normally distributed.
Uses a pooled proportion to calculate the standard error.
Is a z-score.
When the samples are large, the difference between two proportions (p1 - p2) can be approximated to follow a normal distribution. This assumption is based on the Central Limit Theorem.
To calculate the standard error in this scenario, a pooled proportion is used. The pooled proportion combines the proportions from both samples to estimate the common population proportion.
Know more about test statistic here;
https://brainly.com/question/31746962
#SPJ11
hi so the question is, The Expression
\( \frac{4 x}{5} - \frac{2x}{3}\)
is equivalent to which other expression?
A.
\( \frac{x}{2} \)
B.
\( \frac{x}{5} \)
C.
\( \frac{x}{15} \)
D.
\( \frac{2x}{15} \)
Answers
What is the value of the expression -9*2.2?
Answers
Answer:
-19.8
Step-by-step explanation:
2.2(-9) = -19.8
Find the centroid of the region bounded by y=x+3 and y=x²-3. (0,4) (0,1.68) (1.68, 1.098) (1.098,1.68)
Answers
The centroid of the region bounded by the given curves is approximately located at (1.379, 2.897).
To find the centroid, we need to calculate the average x-coordinate and the average y-coordinate of the given points. The x-coordinate of the centroid is obtained by averaging the x-coordinates of the points (0, 4), (0, 1.68), (1.68, 1.098), and (1.098, 1.68). Adding up the x-coordinates and dividing by 4 gives us x-bar ≈ (0 + 0 + 1.68 + 1.098) / 4 ≈ 1.379.
Similarly, the y-coordinate of the centroid is obtained by averaging the y-coordinates of the points. Adding up the y-coordinates and dividing by 4 gives us y-bar ≈ (4 + 1.68 + 1.098 + 1.68) / 4 ≈ 2.897.
Therefore, the centroid of the region bounded by the given curves is approximately located at (1.379, 2.897).
Learn more about centroid here:
https://brainly.com/question/30887628
#SPJ11
The standard normal curve shown below is a probability density curve for a
continuous random variable. This means that the area underneath the entire
curve is 1. What is the area of the shaded region between the two z-scores
indicated in the diagram? z=-1.2 z=0.85
A.0.8937
B.0.6825
C.0.4263
D.0.6375
E.0.6872

Answers
Answer:
E
Step-by-step explanation:
Here, we want to find the area of the shaded portion on the graph.
That would be P(-1.2<z<0.85)
we complete this by checking these values on the standard score table as follows;
P( z< 0.85) - P(z<-1.2) = 0.68727
The table shows the total cost of different numbers of tickets decided whether it makes sense to use a constant rate to describe the relationship
Answers
34.50/6 = 5.75
44/8 = 5.5
52.5/10 = 5.25
As the number of tickets increase, the cost per ticket decreases.
So it does not make sense to use a constant rate.
Answer:34.50/6 = 5.75
44/8 = 5.5
52.5/10 = 5.25
Step-by-step explanation:
As the number of tickets increase, the cost per ticket decreases.
So it does not make sense to use a constant rate.
The list shows numbers in order from least to greatest.
-15,-3,-1.5.2.3,5
Which is an integer that can be inserted on the blank line in the list?
0-2
0 - 11/1
O 0
O 1.2
Answers
The integer that can be inserted on the blank line in the list is: -2
How to complete the number line?The number line is given as:
-15, -3, ____, -1.5, 2, 3, 5
Now, a number line is defined as a line on which numbers are marked at intervals, used to illustrate simple numerical operations.
In this case, we see that the interval of the number line is from -15 to 5.
Thus, the range of values for the blank space will fall in between those two numbers.
Now, since we have positive 2 on the number line, then we must likely also have the negative one to balance it as the blank number.
Read more about Number Line at: https://brainly.com/question/24644930
#SPJ1
-7 4/5 + blank = -9
what is the blank
Answers
Answer:
-1 1/5
Step-by-step explanation:
-9+7 4/5
question above please help due in a few minutes

Answers
Answer:
Step-by-step explanation:
here x\(\geq\)3
the circle is filled so it includes the value
Let (G,⋅) be a group. Prove that Z(G)={g∈G:xg=gx,∀x∈G} is a subgroup of G.
Answers
To prove that the center of a group, Z(G) = {g ∈ G: xg = gx, ∀x ∈ G}, is a subgroup of G, we need to show that it satisfies the three conditions for being a subgroup: closure, identity element, and inverse element.
Let (G, ⋅) be a group, and Z(G) be its center defined as Z(G) = {g ∈ G: xg = gx, ∀x ∈ G}. To prove that Z(G) is a subgroup of G, we need to show that it satisfies the three conditions: closure, identity element, and inverse element.
Closure: Let a, b ∈ Z(G). We need to show that ab^(-1) ∈ Z(G). For any x ∈ G, we have (ab^(-1))x = a(b^(-1)x) = a(xb^(-1)) = (ax)b^(-1) = (xa)b^(-1) = x(ab^(-1)). Therefore, ab^(-1) satisfies the condition for being in Z(G).
Identity Element: The identity element, e, is in Z(G) because for any x ∈ G, ex = xe = x. Inverse Element: Let a ∈ Z(G). We need to show that a^(-1) ∈ Z(G). For any x ∈ G, we have (a^(-1))x = a^(-1)(x) = x(a^(-1)). Therefore, a^(-1) satisfies the condition for being in Z(G).Since Z(G) satisfies the closure, identity, and inverse properties, it is a subgroup of G.
Learn more about subgroup here:
https://brainly.com/question/31432778
#SPJ11
ms tilly garden has an area of 28 1/4 square yards the width of the garden is 2 1/2 yards what is the length in yards of ms tillys garden
Answers
Answer:
length = 11³/₁₀ yards .Step-by-step explanation:
To find:-
The length of the garden in yards.Answer:-
We are here given that the area of MsTilly's garden is 28¼ yards² and the width of the garden is 2½ yards. We are interested in finding out the length of the graden.
Since the garden is rectangle, we can find out it's area as ,
→ Area = length*width
On substituting the respective values, we have;
→ 28¼ = l * 2½
Convert the given mixed fractions into improper fractions as ,
→ 113/4 = l * 5/2
Divide both the sides by 5/2 as ,
→ 113/4 ÷ 5/2 = l
Simplify,
→ 113/4 * 2/5 = l
→ l = 113/10
Convert the improper fraction into mixed fraction as ,
→ l = 11³/₁₀ yards
Hence the length of the garden is 11³/₁₀ yards .
Answer:
The length of Ms Tilly's garden is 11 ³/₁₀ yards.
Step-by-step explanation:
We can model Ms Tilly's garden as a rectangle.
The area of a rectangle is the product of its width and length:
\(\boxed{\sf Area\;of\;a\;rectangle=width \times length}\)
Given that the area of the garden is 28 ¹/₄ square yards and its width is 2 ¹/₂ yards, we can substitute these values into the formula and solve for length to find the length of her garden.
As the values are mixed numbers, begin by converting them into improper fractions.
To convert a mixed number into an improper fraction, multiply the whole number by the denominator of the fraction, add this to the numerator of the fraction, and place the answer over the denominator:
\(\implies 28 \frac{1}{4}=\dfrac{28 \times 4+1}{4}=\dfrac{113}{4}\)
\(\implies 2 \frac{1}{2}=\dfrac{2 \times 2+1}{2}=\dfrac{5}{2}\)
Now substitute the values into the area formula:
\(\begin{aligned} \textsf{Area of the garden}&=\sf width \times length\\\\\implies \dfrac{113}{4}&=\dfrac{5}{2} \times \sf length\end{aligned}\)
To solve the equation for length, divide both sides by ⁵/₂.
Remember that dividing by a fraction is the same as multiplying by the reciprocal of that fraction. Therefore, we can multiply both sides of the equation by ²/₅:
\(\begin{aligned} \textsf{Area of the garden}&=\sf width \times length\\\\\implies \dfrac{113}{4}&=\dfrac{5}{2} \times \sf length\\\\\implies \dfrac{2}{5} \times \dfrac{113}{4}&=\dfrac{2}{5} \times\dfrac{5}{2} \times\sf length\\\\\implies \dfrac{2 \times 113}{5 \times 4}&=\sf length\\\\\implies \textsf{length}&=\dfrac{226}{20}\\\\\implies \textsf{length}&=\dfrac{226\div2}{20\div2}\\\\\implies \textsf{length}&=\dfrac{113}{10}\end{aligned}\)
Finally, convert the improper fraction back into a mixed number by dividing the numerator by the denominator:
\(\implies 113 \div 10=11\;\rm remainder\;3\)
The mixed number answer is the whole number and the remainder divided by the denominator:
\(\implies \dfrac{113}{10}=11 \frac{3}{10}\)
Therefore, the length of Ms Tilly's garden is 11 ³/₁₀ yards.
Solve the following equation for x . 9=x2+2
Answers
Answer:
X=3.5
Step-by-step explanation:
9=x2+2
9-2=x2
(9-2)÷2=x
7. The ratio of basketball players to baseball players at Cypress High School is 4 to 3. If Coach Nelson has 20 basketball players, how many players does he have for basketball and baseball combined?
A. 15
A. 15
B. 140
B. , 140,
C. 35
C. 35
D. none of these
D. none of these
Answers
\( \huge{ \blue{ \frac{4}{3} = \frac{20}{n} }}\)
\( \bold{ = \frac{3 \times 20}{4n} }\)
\( = \frac{60}{4} \)
\( \huge{ \bold{ \gray{ \boxed{ = \boxed{15}}}}}\)
Step 2: Add the number of basketball players and the number of baseball players\( \huge{ \orange{20 + 15}}\)
\( \huge{ \bold{ \red{ \boxed{ = \boxed{35}}}}}\)
Answer:\( \huge{ \bold{ \green{ \boxed{ \boxed{ \underline{c. \: 35}}}}}}\)
#CARRYONLEARNING
Evaluate: Question(2): Z+8-6(z-2a)+5z
Answers
Answer:
Z+12a−z+8+12−+8
Step-by-step explanation:
Z+8−6(z−2a)+5z
+8−6(−2)+5
Z+8−6(−2a+z)+5z
+8−6(−2+)+5
Z+8−6(−2a+z)+5z
+8−6(−2+)+5
Z+8+12a−z+8+12−
Answer:
Z + 8 + 12a − z
12a + 8
Step-by-step explanation:

hello someone help please
what is the product of (cosA+2)(cosA-3)
Answers
Answer:
cos²A - cosA - 6
Step-by-step explanation:
Given
(cosA + 2)(cosA - 3)
Each term in the second factor is multiplied by each term in the first factor, that is
cosA(cosA - 3) + 2(cosA - 3) ← distribute both parenthesis
= cos²A - 3cosA + 2cosA - 6 ← collect like terms
= cos²A - cosA - 6
7. True or False: If a person makes a credit card payment earlier in the month versus later in
the month, it will result in a lower average daily balance, lower interest owed, and a smaller
minimum payment at the end of the billing cycle.
Answers
Answer: True.
explanation: If a person makes a credit card payment earlier in the month versus later in the month, it will result in a lower average daily balance, lower interest owed, and a smaller minimum payment at the end of the billing cycle. Paying off your balance early or making additional payments before the billing cycle ends decreases your credit utilization.
PLEASE ANSWER, HURRY!!!

Answers
Hello!
1/6 ≈ 0.167
the answer is 0.167
1.) Line segment AB has endpoints A(1,8) and B(7,−4). What are the coordinates of the point located 5/6 of the way from A to B?
O (-4, 11 1/3)
O (3, -2 1/3)
O (6, -2)
O (12, -14)
2.) Line segment AB has endpoints B (-3, 0) and A(5, 4). What are the coordinates of the point located 1/4 of the way from B to A?
O (1, -1)
O (1, 2)
O (3, 3)
O (-1, 1)
3.) Line segment AB has endpoints A(1, 8) and B(7, -4). What are the coordinates of the point located 1/6 of the way from A to B?
O (0, 8 2/3
O (2, 6)
O (8 2/3, -3 1/3)
O (6, -3 1/3)
^Please help, ASAP. These were due yesterday, however I am trying to get this done.
BRAINLIEST AND 5 STARS TO CORRECT RESPONSES ONLY! LOTS OF PTS AVAILABLE TO THOSE WHO PARTICIPATE HOWEVER.
Answers
The coordinates of the 3 respective points from the given parameters are; (6, -2); (-1, 1); (2, 6)
How to find the length of Line Segment?1) The coordinates of the point located 5/6 of the way from A to B is;
x = ⁵/₆(7 - 1) + 1
x = 6
y = ⁵/₆(-4 - 8) + 8
y = -2
x, y = (6, -2)
2) The coordinates of the point located ¹/₄ of the way from A to B is;
x = -3 + ¹/₄(5 - (-3))
x = -1
y = 0 + ¹/₄(4 - 0)
y = 1
x, y = (-1, 1)
3) The coordinates of the point located ¹/₆ of the way from A to B is;
x = ¹/₆(7 - 1) + 1
x = 2
y = ¹/₆(-4 - 8) + 8
y = 6
x, y = (2, 6)
Read more about Length of Line Segment at; https://brainly.com/question/27064838
#SPJ1
Select the correct answer from each drop-down menu.
1. If , _____ then ∆ABC and ∆DEF are congruent by the ASA criterion.
A.) AB=DE
B.)CA=FD
C.)Angle B is congruent to angle E
D.)Angle A is congruent to angle D
2. If , ______ then ∆ABC and ∆DEF are congruent by the SAS criterion.
A.) AB=DE
B.)CA=FD
C.)Angle B is congruent to angle E
D.)Angle A is congruent to angle D
3. ∆ABC and ∆DEF are congruent if
A.) Angle A is congruent to angle D
B.) AB=DE
C.) AB=DF
Answers
ASA: ∆ABC and ∆DEF are congruent if angle B is congruent to angle E. SAS: ∆ABC and ∆DEF are congruent if angle A is congruent to angle D and AB=DE.
What is congruent ?
In geometry, congruent refers to the condition where two or more figures have the same size and shape. Congruent figures have the same dimensions, angles, and proportions. Two figures are congruent if they can be superimposed exactly on each.
1) If, C.) Angle B is congruent to angle E then ∆ABC and ∆DEF are congruent by the ASA criterion.
2) If, D.) Angle A is congruent to angle D then ∆ABC and ∆DEF are congruent by the SAS criterion.
3) ∆ABC and ∆DEF are congruent if B.) AB=DE
ASA criterion: If in two triangles, two angles and the included side of one triangle are congruent to the corresponding parts of the other triangle, the two triangles are congruent.
ASA: ∆ABC and ∆DEF are congruent if angle B is congruent to angle E. SAS: ∆ABC and ∆DEF are congruent if angle A is congruent to angle D and AB=DE.
To learn more about congruent visit : brainly.com/question/12413243
#SPJ4
solve the following equation for x. Round any decimal to the nearest hundredth place ln 4^(x+3)= ln3^-3
Answers
Using the properties of logarithms we have that:
\(\begin{gathered} 4^{x+3}=3^{-x} \\ \log _2(4^{x+3})=\log _2(3^{-x}) \\ 2(x+3)=-x\log _2(3) \\ 2x+6=-x\log _2(3) \\ 2x+x\log _2(3)=-6 \\ x(2+\log _2(3))=-6 \\ x=-\frac{6}{2+\log _2(3)} \end{gathered}\)x has a value of -6/(2+log₂(3))
9) an employment agency wishes to place 125 employees into desirable statistical groups based on the time they spent commuting to work. The shortest time is 5 minutes and the longest commuting time is 120 minutes.
The first group will have commuting time of _____
A) none of the options
B) 0-15 minutes
D) 5-15 minutes
E) 5-20 minutes
Answers
Option (B) is correct. The first group will have a commuting time of 0-15 minutes, as it covers the desired range and includes the shortest commuting time of 5 minutes.
The first group will have a commuting time of 0-15 minutes. This range is selected because it covers the desired commuting time range of 5-120 minutes. Since the shortest commuting time is 5 minutes, a range starting from 0 minutes would include it. Additionally, the upper limit of 15 minutes ensures that employees with longer commuting times are not included in this group.
By placing employees with commuting times ranging from 0-15 minutes in the first group, the employment agency can create a statistical grouping that represents those who have relatively short commutes. This grouping allows for better analysis and understanding of the distribution of commuting times among the 125 employees and can aid in making informed decisions regarding job placements and other related factors.
To learn more about distribution , click here:
brainly.com/question/28060657
#SPJ11
Help me 20 points ........................

Answers
Answer:
Step-by-step explanation:
First, you need to find the slope of the line. To do this you need to choose two points on the graph. The points you are given are (-2, 1) and (4, 6). Then use these to find the slope.
\(m=\frac{y2-y1}{x2-x1}\)
\(m=\frac{6-1}{4-(-2)}\)
\(m=\frac{5}{6}\)
You can then plug this and one of your chosen points into the slope-intercept formula
\(y-y=m(x-x)\)
\(y-1=\frac{5}{6} (x-(-2))\)
\(y-1=\frac{5}{6} x+\frac{5}{3}\)
\(y=\frac{5}{6}x+\frac{8}{3}\)
Find the missing number based on the description below. 11 less than four times a number is the same as 46 less than the product of -1 and the number
Answers
Given:
11 less than four times a number is the same as 46 less than the product of -1 and the number.
To find:
The missing number.
Solution:
Let x be the missing number.
Four times a number = 4x
11 less than four times a number = 4x-11
Product of -1 and the number = (-1)x
= -x
46 less than the product of -1 and the number = -x-46
The given statement is "11 less than four times a number is the same as 46 less than the product of -1 and the number". So,
\(4x-11=-x-46\)
\(4x+x=11-46\)
\(5x=-35\)
Divide both sides by 5.
\(x=\dfrac{-35}{5}\)
\(x=-7\)
Therefore, the missing number is -7.
Construct the exponential function that contains the points (0,-2) and (3,-128) Provide your answer below:
Answers
To construct the exponential function that contains the points (0,-2) and (3,-128), we can use the general form of an exponential function:
y = a * b^x
where y is the function value, x is the input value, b is the base of the exponential function, and a is a constant representing the y-intercept. To find the specific exponential function that contains the two given points, we need to solve for a and b using the given coordinates.
First, we can use the point (0,-2) to find the value of a:
-2 = a * b^0
-2 = a * 1
a = -2
Next, we can use the point (3,-128) to find the value of b:
-128 = -2 * b^3
64 = b^3
b = 4
Now that we know the values of a and b, we can write the exponential function:
y = -2 * 4^x
Therefore, the exponential function that contains the points (0,-2) and (3,-128) is y = -2 * 4^x.
To view a related problem visit : https://brainly.com/question/18891502
#SPJ11
Find the linear approximation to g(y) Cos(y+1) at y = 0. Use the linear approximation to approximate the value of Cos (2) and Cos(15). Compare the approximated values to the exact value. (15 pts)
11) Estimate the value of Csc (0.2) using linear approximation and without using any kind of computational aid. (20 points)
Answers
Approximation of cos(15) from linear approximation: L(15) ≈ cos(1) - 15sin(1) ≈ 0.540302305868 - 15(0.841470984808) ≈ -11.0905365065
We cannot estimate the value of csc(0.2) using linear approximation without any computational aid.
First, let's find the derivative of g(y) with respect to y:
g'(y) = -sin(y+1)
Next, we evaluate g'(y) at y = 0:
g'(0) = -sin(0+1) = -sin(1)
The linear approximation to g(y) at y = 0 can be expressed as:
L(y) = g(0) + g'(0)(y - 0)
Since g(0) = cos(0+1) = cos(1), the linear approximation becomes:
L(y) = cos(1) - sin(1)y
To approximate the values of cos(2) and cos(15) using the linear approximation, we substitute the respective values of y into L(y):
Approximation of cos(2):
L(2) = cos(1) - sin(1)(2) = cos(1) - 2sin(1)
Approximation of cos(15):
L(15) = cos(1) - sin(1)(15) = cos(1) - 15sin(1)
To compare the approximated values to the exact values, we need to compute the exact values of cos(2), cos(15), and csc(0.2).
cos(2) ≈ 0.41614683654 (approximated using a calculator)
cos(15) ≈ 0.96592582629 (approximated using a calculator)
csc(0.2) ≈ 5.02553333034 (approximated using a calculator)
Now we can compare the approximated values using the linear approximation to the exact values:
Approximation of cos(2) from linear approximation: L(2) ≈ cos(1) - 2sin(1) ≈ 0.540302305868 - 2(0.841470984808) ≈ -1.14264104833
Error: |exact value - approximation| = |0.41614683654 - (-1.14264104833)| ≈ 1.55878788487
Approximation of cos(15) from linear approximation: L(15) ≈ cos(1) - 15sin(1) ≈ 0.540302305868 - 15(0.841470984808) ≈ -11.0905365065
Error: |exact value - approximation| = |0.96592582629 - (-11.0905365065)| ≈ 12.0564623328
For csc(0.2), we need to use a different approach as it involves the cosecant function. The linear approximation is not directly applicable to this trigonometric function. Therefore, we cannot estimate the value of csc(0.2) using linear approximation without any computational aid.
Learn more about approximation here : brainly.com/question/29669607
#SPJ11
The school is making this sidewalk six times longer.
Width = 5 feet
Length = 30 feet
Enter the new length of the sidewalk, in feet.
Enter the new area of the sidewalk, in square feet.
feet
square feet
Answers
Answer:
Area = 150
Step-by-step explanation:
Since the sidewalk is mostly rectangular in shape, we shall do the steps below.
Lengths more the school is making the sidewalk longer = 6x (6 times)
Width of the sidewalk = 5 ft
Length of the sidewalk = 30 ft
Area of the sidewalk
= Area = LxB
= Area = 5x30
= Area = 150
lemont has 30 books to pack the boxes each box holds 7 books if he fills each box how many boxes are left over
Answers
Answer:
2 books
Step-by-step explanation:
If 7 books= 1 box
Then 30 books= 30÷7= 4 boxes with a remainder of 2 books
Therefore books left over= 2 books
evaluate the expression 6x + 4 9/10 when x = 2/3.
Answers
x=2/3
6(2/3) + 4 9/10 =4 + 4 9/10 = 8 9/10
Answer:
2x-1=y,2y+3=x
Step-by-step explanation:
no explanation
Solve for X. Assume that lines that appear Tangent are Tangent.
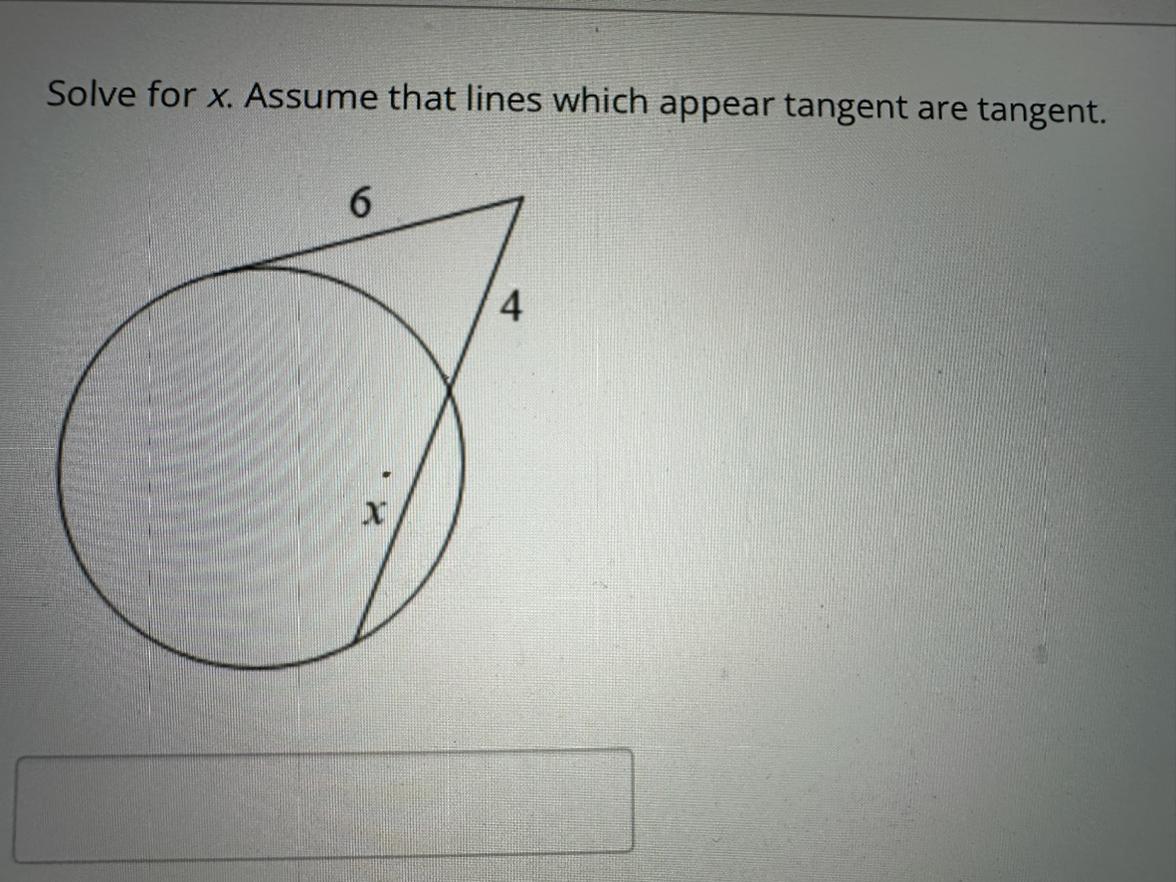
Answers
The value of x in the secant segment is 5.
What is the value of x?The secant-tangent power theorem states that "if a tangent and a secant are drawn from a common external point to a circle, then the product of the length of the secant segment and its external part is equal to the square of the length of the tangent segment".
( tangent segment )² = External part of the secant segment × Secant segment.
From the image:
Tangent segment = 6
External part of the secant segment = 4
Secant segment = ( 4 + x )
Plug these values into the above formula and solve for x.
( tangent segment )² = External part of the secant segment × Secant segment.
6² = 4 × ( 4 + x )
Simplify
36 = 16 + 4x
4x = 36 - 16
4x = 20
x = 20/4
x = 5
Therefore, the value of x is 5.
Learn more about secant tangent power theorem here: brainly.com/question/26407978
#SPJ1