enter the value of n so that the expression (-y+4)+(8y-9) is equivalent yo ny -5
Answers
The Value of n so that the expression (-y + 4) + (8y - 9) is equivalent to ny - 5 is n = 7.
The value of n so that the expression (-y + 4) + (8y - 9) is equivalent to ny - 5,
we need to equate the coefficients of y and the constant terms in both expressions.
So, let's start by simplifying the given expression: (-y + 4) + (8y - 9) = -y + 8y - 5 = 7y - 5
Now, we can equate this with the given expression, which is ny - 5.
Equating coefficients of y, we get: 7y = ny ⇒ n = 7
Equating the constant terms, we get: -5 = -5
Thus, the value of n so that the expression (-y + 4) + (8y - 9) is equivalent to ny - 5 is n = 7.
For more questions on Value .
https://brainly.com/question/843074
#SPJ8
Related Questions
Mrs.Lewis bought 100 yards of ribbon.She used some of the ribbon to decorate dresses .Now she has 67 yards of ribbon remaining. How many yards of ribbon did Mrs.Lewis use to decorate the dresses?
Answers
Answer:
33 yards
Step-by-step explanation:
To find the number of ribbons that she used to decorate the dresses can be gotten by subtracting the amount of ribbon left from the total amount of ribbon she had.
She bought 100 yards. She has 67 yards left.
Therefore, the amount of ribbon she used for the dresses is:
100 - 67 = 33 yards
can someone help plz


Answers
Answer:
the second picture answer is F.56
Step-by-step explanation:
if you add 16 + 40=56
factorize. (x+y)) ^24x^2y^2
Answers
Answer:
I guess this is the answer
Step-by-step explanation:
(x + y)²4x²y²
= [2xy(x + y)]²
= (2x²y²)²
Colleen has a wooden board that is 12 3/4 feet long. She cuts the board into three pieces. Two of the pieces are both 4 7/12 feet long.
How long is the other piece of Colleen's board?
Answers
Answer:
Step-by-step explanation: I don’t know
A bicycle manufacturer is studying the reliability of one of its models. the study finds that the probability of a brake defect is 4 percent and the probability of both a brake defect and a chain defect is 1 percent. if the probability of a defect with the brakes or the chain is 6 percent, what is the probability of a chain defect? 1.5 percent 2 percent 2.5 percent 3 percent
Answers
Using Venn probabilities, it is found that there is a 0.03 = 3% probability of a chain defect.
What is a Venn probability?In a Venn probability, two non-independent events are related to each other, as are their probabilities.
The "or probability" is given by:
\(\rm P(A \cup B ) = P(A)+P(B)-P(A\cap B)\)
In this problem, the events are:
Event A: Brake defect.
Event B: Chain defect.
For the probabilities, we have that:
The study finds that the probability of a brake defect is 4 percent, P(A) = 0.04.The probability of both a brake defect and a chain defect is 1 percent, P(A∩B) = 0.01.The probability of a defect with the brakes or the chain is 6 percent, P(A∪B) = 0.06.Substitute all the values in the formula
\(\rm P(A \cup B ) = P(A)+P(B)-P(A\cap B)\\\\0.06=0.04+P(B)-0.01\\\\P(B)=0.06-0.04+0.01\\\\ P(B)=0.03\)
0.03 = 3% probability of a chain defect.
Hence, there is a 0.03 = 3% probability of a chain defect.
You can learn more about Venn probabilities at brainly.com/question/25698611
Answer:
D
Step-by-step explanation:
Amir operates a large lobster boat. The operating cost for the boat is $2.250 each day. At the end of each day, he sells all his freshly caught lobster to either the local restaurant or the local grocery store with the following conditions:
• The price per pound that the restaurant is willing to pay follows a triangular distribution with minimum value $1.50, maximum value $5.50, and likeliest value $3.50.
• The price per pound that the grocery store is willing to pay is decreasing with more lobsters: $3.85 - 50.0005 * y, where y is the total lobster amount sold in pounds.
• The amount of lobster that Amir catches in a single day follows a normal distribution with mean 1,500 pounds and standard deviation sqrt(12,500) pounds.
Amir decides to sell a fixed percentage of lobster to the local restaurant and the rest to local grocery stores. Using either math or simulation, can you help Amir determine what percentage he should choose in order to maximize his expected profit in the long run?
Previous question
Answers
The expected profit in the long run can be determined by calculating the expected value of the total revenue from selling the lobsters. The expected total revenue is the sum of the expected revenue from selling the lobsters to the restaurant and the from selling the lobsters to the grocery store.
The expected value of the revenue from selling the lobsters to the restaurant can be calculated by multiplying the expected price per pound from the restaurant by the expected amount of lobsters caught in a day. The expected price per pound from the restaurant follows a triangular distribution with minimum value $1.50, maximum value $5.50, and likeliest value $3.50. The expected amount of lobsters caught in a day follows a normal distribution with mean 1,500 pounds and standard deviation sqrt(12,500) pounds.
The expected value of the revenue from selling the lobsters to the grocery store can be calculated by multiplying the expected price per pound from the grocery store by the expected amount of lobsters caught in a day. The expected price per pound from the grocery store is decreasing with more lobsters: $3.85 - 50.0005 * y, where y is the total lobster amount sold in pounds. The expected amount of lobsters caught in a day follows a normal distribution with mean 1,500 pounds and standard deviation sqrt(12,500) pounds.
Given the expected values of the total revenue from selling the lobsters to the restaurant and the grocery store, Amir can use simulation to determine the optimal percentage of lobsters to sell to the restaurant in order to maximize his expected profit in the long run. He can run several simulations with different percentages of lobsters to be sold to the restaurant and compare the expected profits for each simulation. The percentage that produces the highest expected profit is the optimal percentage for Amir to maximize his expected profit in the long run.
Amir can use simulation to determine the optimal percentage of lobsters to sell to the restaurant in order to maximize his expected profit in the long run. He can calculate the expected value of the total revenue from selling the lobsters to the restaurant and the grocery store, and then run several simulations with different percentages of lobsters to be sold to the restaurant to compare the expected profits for each simulation. The percentage that produces the highest expected profit is the optimal percentage for Amir to maximize his expected profit in the long run.
Learn more about profit here
https://brainly.com/question/33585
#SPJ4
What values on a number line will give me the absolute
value of 3?
Answers
Which is the best approximate solution of the system of linear equations y= -1 and y= 1?
Graph
Answers
There is no "best approximate solution" for this system of linear equations since no solution exists.
The given system of linear equations is y = -1 and y = 1. These are two horizontal lines parallel to the x-axis, where one line is located at y = -1 and the other at y = 1.
When we solve this system of equations, we find that there is no common solution for the variables x and y. The lines y = -1 and y = 1 do not intersect, meaning there is no point that satisfies both equations simultaneously.
On a graph, these two lines will appear as parallel lines running horizontally at different heights on the y-axis. They will never cross or intersect.
Therefore, there is no "best approximate solution" for this system of linear equations since no solution exists.
for such more question on linear equations
https://brainly.com/question/19803308
#SPJ8
Fiona asked her team to suggest ways of surveying the population of their middle school to find out how many students use bottled water.
Which student has the method that is most representative of the school’s population?
Raina suggested that she ask everyone in her math class on Friday.
Miya suggested that she ask students sitting in the first row of her classes on Friday.
Ryo suggested that he ask the basketball players at his practice on Friday.
Amir suggested that he ask every tenth student as he or she walks into school in the morning.
Answers
The students who has the method that is most representative of the school’s population is Amir.
What is a population?Population refers to the group of people being studied in an experiment or the group from which a sample is drawn.
Amir has the method that is most representative of the school’s population because the method includes all students in the school studying different subjects but picked at random (every tenth students)
Learn more about population survey:
https://brainly.com/question/7301139
#SPJ1
what is the surface area of the cube with edge length = 3 inches? 54 square inches 9 square inches 18 square inches 27 square inches 3
Answers
The surface area of a cube with an edge length of 3 inches is 9 square inches * 6 = 54 square inches.
The surface area of a cube can be calculated by finding the area of each face and summing them up.
For a cube with an edge length of 3 inches, the surface area can be determined as follows:
Each face of the cube is a square, and since all sides of a cube are equal, the area of each face is (3 inches * 3 inches) = 9 square inches.
Since a cube has six faces, we multiply the area of one face by 6 to find the total surface area.
Therefore, the surface area of a cube with an edge length of 3 inches is 9 square inches * 6 = 54 square inches.
Hence, the correct answer is 54 square inches.
Learn more about total surface area here:
https://brainly.com/question/8419462
#SPJ11
use a 99 percent confidence interval to estimate the difference between the mean wait times for ambulance transported patients and self-transported patients at this emergency room. based only on this confidence interval, do you think the difference in the mean wait times is statistically significant? justify your answer.
Answers
A 99% confidence interval for the difference in mean wait times for ambulance and self-transported patients is (0.15, 3.33) minutes. Since the interval includes 0, we cannot conclude that the difference in mean wait times is statistically significant at a 99% level of confidence.
To estimate the difference between the mean wait times for ambulance-transported patients and self-transported patients, we can use the two-sample t-interval for the difference in means, assuming equal variances:
\($\bar{x}_1 - \bar{x}2 \pm t{\alpha/2, n_1 + n_2 - 2} \times \sqrt{\frac{s_p^2}{n_1}+\frac{s_p^2}{n_2}}$\)
\($\bar{x}1$ and $\bar{x}2$\)where are the sample means, \($s_p$\) is the pooled standard deviation, \($n_1$\) and \($n_2$\) are the sample sizes, and\($t{\alpha/2, n_1 + n_2 - 2}$\) is the critical value from the t-distribution with\($n_1 + n_2 - 2$\) degrees of freedom.
Substituting the given values, we get:
\($\bar{x}_1 - \bar{x}_2 \pm 2.626 \times \sqrt{\frac{8.30^2}{77}+\frac{5.16^2}{73}}$$\implies 6.04 - 4.30 \pm 2.626 \times \sqrt{\frac{8.30^2}{77}+\frac{5.16^2}{73}}$\)
\($\implies 1.74 \pm 1.59$\)
Thus, the 99% confidence interval for the difference between the mean wait times is (0.15, 3.33) minutes.
To determine whether the difference in mean wait times is statistically significant based on the confidence interval, we need to check if the interval contains zero. Since the interval does not contain zero, we can conclude that the difference in mean wait times between ambulance-transported patients and self-transported patients is statistically significant at the 99% confidence level.
To know more about confidence interval:
https://brainly.com/question/29680703
#SPJ4
--The given question is incomplete, the complete question is given
"Patients with heart-attack symptoms arrive at an emergency room either by ambulance or self- transportation provided by themselves, family, or friends. When a patient arrives at the emergency room, the time of arrival is recorded. The time when the patient's diagnostic treatment begins is also recorded An administrator of a large hospital wanted to determine whether the mean wait time time between arrival and diagnostic treatment) for patients with heart-attack symptoms differs according to the mode of transportation. A random sample of 150 patients with heart-attack symptoms who had reported to the emergency room was selected. For each patient, the mode of transportation and wait time were recorded. Summary statistics for each mode of transportation are shown in the table below. Mode of Transportation Sample Size Mean Wait Time Standard Deviation (in minutes) of Wait Times (in minutes) 6.04 4.30 8.30 5.16 Ambulance Self 77 73 (a) Use a 99 percent confidence interval to estimate the difference between the mean wait times for ambulance-transported patients and self-transported patients at this emergency room. You may assume that conditions for inference are met. (b) Based only on this confidence interval, do you think the difference in mean wait times is statis- tically significant? Justify your answer."--
A graphical device used for enumerating sample points in a multiple-step experiment is a:.
Answers
A graphical device used for enumerating sample points in a multiple-step experiment is a tree diagram.
A tree diagram is a way of determining probabilities of different outcomes based on numerous different events.
It helps in identifying all the probable outcomes of an experiment and helps in understanding the likelihood of each of these events.
A tree diagram starts with a single root node that is then divided into different branches based on the potential outcomes of an experiment that are mutually exclusive.
These branches then split again into sub-branches until the final potential outcomes of an experiment are reached.
Know more about a tree diagram here:
https://brainly.com/question/24391505
#SPJ11
(¡) calculate the volume of the solid
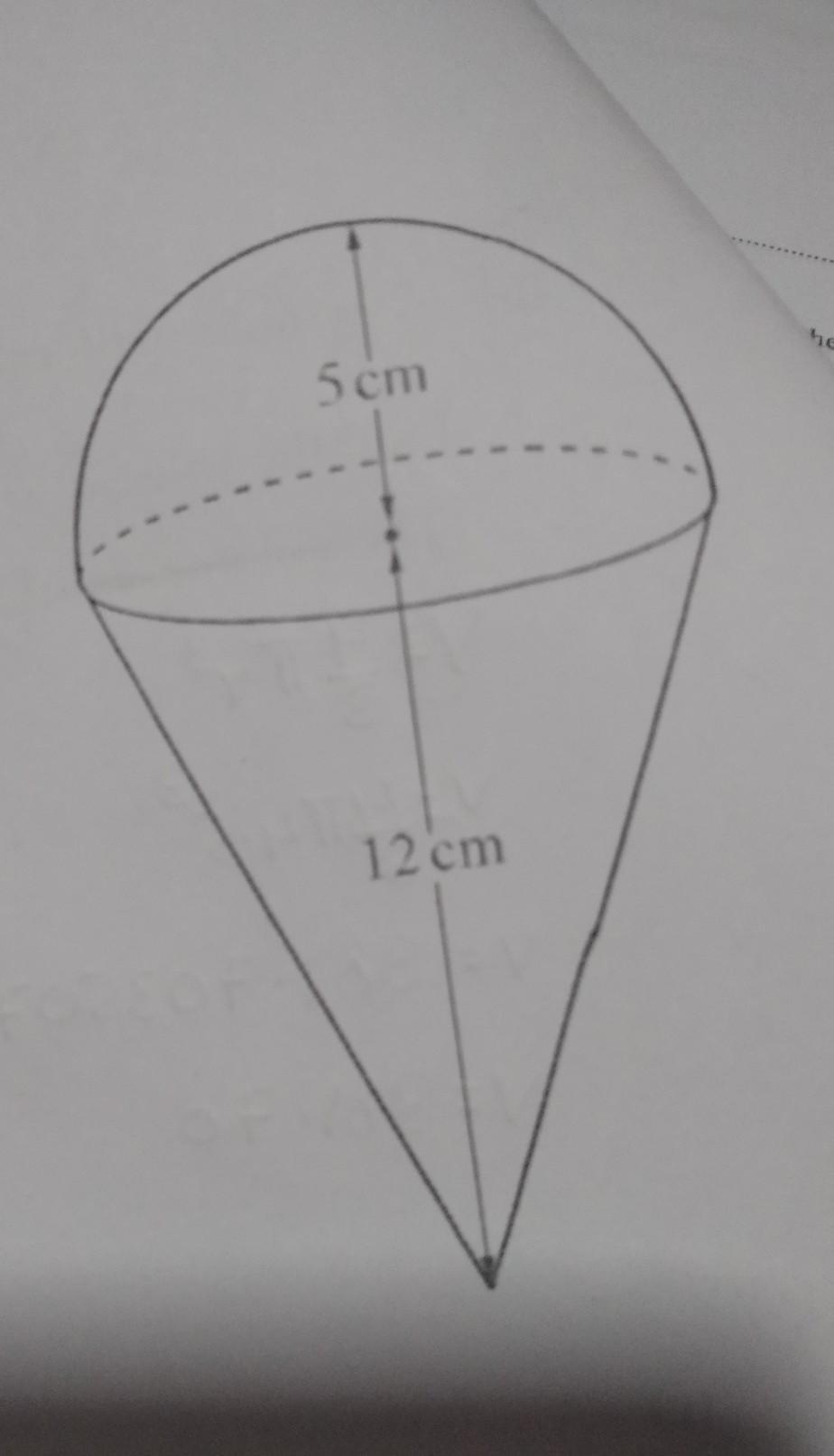
Answers
Answer:
\(\frac{550}{3} \pi \) cm³ = 576 cm³ (3 sf)
Step-by-step explanation:
Height of hemisphere = 5 cm therefore, radius (r) = 5
Volume of a hemisphere = \(\frac{2}{3} \pi r^3\) = \(\frac{2}{3} \pi \times 5^3\) = \(\frac{250}{3} \pi \)
Volume of a cone = \(\frac{1}{3} \pi r^2h\) = \(\frac{1}{3} \pi \times 5^2 \times 12\) = \(100\pi \)
Total volume of solid = \(\frac{250}{3} \pi +100\pi =\frac{550}{3} \pi =\) 576 cm³ (3 sf)
Which of these statements correctly interprets what it means to be "95% confident"? Choose the correct answer below. A. 95% of samples will produce a confidence interval that captures the true proportion. B. 95% of the time, the sample proportion will be in the interval. C. 95% of the sample is in the confidence interval.
Answers
95% of samples will produce a confidence interval that captures the true proportion. The correct answer is A.
When we say we are 95% confident in a particular interval estimate, it means that if we were to take many different samples from the same population and compute a confidence interval for each sample using the same method, about 95% of those intervals would contain the true population parameter.
So, Option A correctly states that 95% of samples will produce a confidence interval that captures the true proportion. Option B is incorrect because it refers to the sample proportion, rather than the true population proportion. Option C is also incorrect because it refers to the sample, rather than the confidence interval.
For more information about proportion, visit:
https://brainly.com/question/19994681
#SPJ11
if we select 4 young american men at random, what is the probability that they are all 68 inches or shorter (that is, each one of them is 68 inches or shorter)? enter your answer as a numerical value rounded to three decimal places (for ex., 0.111, no text).
Answers
The estimated probability that all four randomly selected young American men are 68 inches or shorter is approximately 0.004 or 0.4%.
To calculate the probability that all four randomly selected young American men are 68 inches or shorter, we need to consider the probability for each individual man and multiply them together.
Let's assume that the probability of an individual young American man being 68 inches or shorter is p. Since we are selecting four men at random, the probability of each man being 68 inches or shorter is the same, and we can multiply their probabilities together.
The probability of one man being 68 inches or shorter is p. Therefore, the probability of all four men being 68 inches or shorter is p × p × p × p = p^4.
However, we are not given the specific value of p in the problem statement. If we assume that the height of young American men follows a normal distribution, we can look up the corresponding z-score for a height of 68 inches or shorter and use the standard normal distribution to estimate the probability.
For example, if we find that a height of 68 inches corresponds to a z-score of -1.0, we can use a standard normal distribution table or a calculator to determine the probability of a z-score less than or equal to -1.0. Let's say this probability is approximately 0.1587.
Therefore, the estimated probability that all four randomly selected young American men are 68 inches or shorter would be (0.1587)^4 = 0.004.
Thus, the probability is approximately 0.004 or 0.4% rounded to three decimal places.
For more such questions on probability visit:
https://brainly.com/question/30768613
#SPJ8
Find the area of a regular octagon with
a side length of 8 cm. Round to the
nearest tenth.
8 cm
[? ] cm2
Enter
![Find the area of a regular octagon witha side length of 8 cm. Round to thenearest tenth.8 cm[? ] cm2Enter](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/OwnTqKz2OfYgoZd0JFHYvwzgkrw7D6bS.png)
Answers
Answer:
Step-by-step explanation:
Area=2(1+\(\sqrt{2}\))8²
=309.0(round to nearest tenth)
Which best describes the graph of the line that has slope of -2/5 and passes through (10, -2) and the line that passes through (0,1) and (5,-1)?
A) coincident lines
B) intersecting lines
C) parallel lines
D) vertical lines
Answers
Answer:
The line with a slope of -2/5 and passing through (10,-2) can be expressed in point-slope form as:
y - (-2) = (-2/5)(x - 10)
Simplifying this equation gives:
y = (-2/5)x + 2
The line passing through (0,1) and (5,-1) can be expressed in slope-intercept form as:
y - 1 = [-1 - 1]/[5 - 0](x - 0)
Simplifying this equation gives:
y = -0.4x + 1
Since the two lines have different slopes (-2/5 and -0.4), they are not parallel. To determine if they intersect, we can set the two equations equal to each other and solve for x:
(-2/5)x + 2 = -0.4x + 1
0.2x = 1
x = 5
Substituting x = 5 into either equation gives:
y = (-2/5)(5) + 2 = 0
Therefore, the two lines intersect at the point (5,0), and the answer is B) intersecting lines.
A piece of wire 20 cm long is bent in the shape of a triangle with interior angles 30, 60 and 90 . Find the length of the hypotenuse, giving your answer in surd form with rational denominator
Answers
Answer:
(60 - 20√3) / 3
Step-by-step explanation:
In a right-angled triangle, a ² + b ² = c ²
call the length of the opposite x and the adjacent x√3.
A 30, 60, 90 triangle takes the form x² + (x√3 )²
= x² + 3x²
= 4x² = hypotenuse²
hypotenuse = 2x.
so 2x + x + x√3 = 20
3x + x√3 = 20
x (3 + √3) = 20
x = 20 ÷ (3 + √3)
hypotenuse = 2x.
2x = 2 X [20 ÷ (3 + √3) ]
= 40 ÷ (3 + √3)
= [ 40 ÷ (3 + √3)] X [(3 - √3) ÷ (3 - √3)]
= (120 - 40√3) ÷ (9 - 3)
= (120 - 40√3) ÷ 6
= (60/3) ÷ [(20√3) / 3]
= (60 - 20√3) / 3
The length of the hypotenuse (side "c") is 20 cm.
Let's denote the sides of the triangle as follows:
Let "a" be the side opposite the 30-degree angle.
Let "b" be the side opposite the 60-degree angle.
Let "c" be the hypotenuse opposite the 90-degree angle.
We know that the sum of the interior angles of any triangle is 180 degrees, so:
30 + 60 + 90 = 180
Now, let's use the Law of Sines to relate the side lengths and the angles of the triangle:
a/sin(30) = b/sin(60) = c/sin(90)
Since sin(30) = 1/2, sin(60) = √3/2, and sin(90) = 1, we can rewrite the equation as:
a/(1/2) = b/(√3/2) = c/1
Now, let's simplify:
a/(1/2) = 2a
b/(√3/2) = 2b/√3
c/1 = c
The piece of wire is 20 cm long, and this forms the perimeter of the triangle:
a + b + c = 20
Now, let's substitute the simplified expressions into the perimeter equation:
2a + 2b/√3 + c = 20
To make the denominator rational, we can multiply the equation by √3:
2√3a + 2b + √3c = 20√3
Now, we have two equations:
2√3a + 2b + √3c = 20√3
2a + 2b + c = 20
Let's use these equations to solve for "c." Subtract the second equation from the first:
(2√3a + 2b + √3c) - (2a + 2b + c) = 20√3 - 20
Simplifying:
(2√3a - 2a) + (√3c - c) = 20√3 - 20
Factor out "a" and "c":
2a(√3 - 1) + c(√3 - 1) = 20√3 - 20
Now, divide both sides by (√3 - 1):
c = (20√3 - 20) / (√3 - 1)
To rationalize the denominator, we need to multiply the numerator and denominator by the conjugate of (√3 - 1), which is (√3 + 1):
c = [(20√3 - 20) / (√3 - 1)] * [(√3 + 1) / (√3 + 1)]
c = [20√3(√3 + 1) - 20(√3 + 1)] / [(√3 - 1)(√3 + 1)]
c = (20√3(√3) + 20√3 - 20√3 - 20) / (3 - 1)
c = (60 - 20) / 2
c = 40 / 2
c = 20
Therefore, the length of the hypotenuse (side "c") is 20 cm.
To know more about hypotenuse:
https://brainly.com/question/16893462
#SPJ2
is 63/20 equivalent to 4/9 divided by 5/7
Answers
Answer:
No
Step-by-step explanation:
4/9 divided by 5/7 is equal to 4/9 * 7/5 = 28/45. We can see that 63/20 is not equivalent to 28/45 as 28/45 is less than one and 63/20 is greater than one.
Could you please help. Thank you, also show me that solutions!

Answers
\(~~~~~~ \textit{Simple Interest Earned Amount} \\\\ A=P(1+rt)\qquad \begin{cases} A=\textit{accumulated amount}\dotfill & \pounds 1153.76\\ P=\textit{original amount deposited}\dotfill & \pounds 1100\\ r=rate\to r\%\to \frac{r}{100}\\ t=years\dotfill &4 \end{cases}\)
\(1153.76 = 1100[1+(\frac{r}{100})(4)] \implies \cfrac{1153.76}{1100}=1+\cfrac{r}{25}\implies \cfrac{1153.76}{1100}=\cfrac{25+r}{25} \\\\\\ 25\left( \cfrac{1153.76}{1100} \right)=25+r\implies \cfrac{1153.76}{44}=25+r \\\\\\ \cfrac{1153.76}{44}-25=r\implies \stackrel{ \% ~~ }{\boxed{1.22\approx r}}\)
Someone help worth 5 points :( help?

Answers
Answer:
29
Step-by-step explanation:
Answer:
29
Step-by-step explanation:
Since 3x and 87 are the same length, all we need to do is 87 divided by 3.
In the system shown below, what are the coordinates of the solution that lies in quadrant lll? 2x^2+y^2=33. X^2+y^2+2y=19
Answers
By applying the graphical approach, the solution of the nonlinear system that lies in the third quadrant of the Cartesian plane is the point (x, y) = (- 2, -5).
How to find the solution of two nonlinear equations
The first equation corresponds to an ellipse whose major axis is vertical and the second equation is another ellipse with similar characteristics. There are two manners to determine the solution of the given system: (i) Analytical, (ii) Graphical.
In this situation we decide to use a graphical approach, which consists in plotting each function on a Cartesian plane. We use a graphing tool herein.
Please notice that the third quadrant of the Cartesian plane is the region of the plane such that x < 0 and y < 0. The solution of the nonlinear system that lies in the third quadrant is (x, y) = (- 2, -5).
To learn more on ellipses: https://brainly.com/question/14281133
#SPJ1

Answer:
Quadrant III: (-2,-5)
Quadrant IV: (2,-5)
Step-by-step explanation:
Graphed the equations as a system and then found the points that intersect on the graph of each quadrant + was marked correct on APEX
Intro You want to buy a house financed with a 20-year fixed-rate mortgage that makes even monthly payments. The best annual interest rate, stated as an effective annual rate (i.e. the compound rate, "the right thing") you could find is EAR=8%. Part 1 - Attempt 1/1 What is the most you can borrow if you can only afford to pay $1,700 per month?
Answers
We can calculate the maximum amount you can borrow (PV) using the formula mentioned above and the given monthly payment: PV = $1,700 * ((1 - (1 + r)^(-n)) / r)
To determine the maximum amount you can borrow for the house, considering the monthly payment you can afford and the 20-year fixed-rate mortgage, we can use the formula for the present value of an annuity.
The formula is:
PV = PMT * ((1 - (1 + r)^(-n)) / r)
Where:
PV is the present value (loan amount)
PMT is the monthly payment
r is the monthly interest rate
n is the total number of payments
First, we need to convert the effective annual interest rate (EAR) to a monthly interest rate. Since there are 12 months in a year, the monthly interest rate (r) can be calculated as:
r = (1 + EAR)^(1/12) - 1
Plugging in the given values:
EAR = 8% = 0.08
r = (1 + 0.08)^(1/12) - 1
Next, we need to calculate the total number of payments (n) based on the loan term. In this case, since it's a 20-year mortgage with even monthly payments, the total number of payments is:
n = 20 years * 12 months/year
Substituting the values, we can calculate the maximum loan amount.
Know more about present value here:
https://brainly.com/question/28304447
#SPJ11
Question
Divide.
1582
Enter your answer as a mixed number in simplest form by filling in the boxes.
$$
Answers
Answer:
1582÷
Step-by-step explanation:
because u haven't told to divide wth any number
Answer:
Your question isn't complete. Kindly correct it.
A certain type of device has an advertised failure rate of 0.0025 per hour. The failure rate is constant and the exponential distribution applies.
a) What is the mean time to failure?
b) What is the probability that 1200 hours will pass before a failure is observed?
Answers
a) The failure rate of the device = 0.0025 per hour, in the exponential distribution, the mean time to failure is given by MTTF (Mean Time To Failure).
b) The probability that 1200 hours will pass before a failure is observed is approximately 0.368 or 36.8%.
We can find the mean time to failure of the device by using the exponential distribution formula.
MTTF = 1/λwhere
λ is the failure rate, so:
MTTF = 1/0.0025= 400 hours
Therefore, the mean time to failure is 400 hours.
b) To find the probability that 1200 hours will pass before a failure is observed, we can use the cumulative distribution function of the exponential distribution:
P(X > 1200) = e^(-λt), where
t is the time passed.
In this case, t = 1200 hours, so:
P(X > 1200) = \(e^{(-0.0025 * 1200)}\) ≈ 0.368
Therefore, the probability that 1200 hours will pass before a failure is observed is approximately 0.368 or 36.8%.
The formula gives us the average amount of time before a failure occurs, and it is found to be 400 hours.
This means that we can expect a failure to occur every 400 hours, on average.
To find the probability that 1200 hours will pass before a failure is observed, we use the cumulative distribution function of the exponential distribution.
The function gives us the probability that the time to failure is greater than a certain value.
In this case, we want to find the probability that 1200 hours will pass before a failure is observed, so we use the formula with t = 1200.
The result is a probability of approximately 0.368 or 36.8%.
To know more about exponential distribution, visit:
https://brainly.com/question/22692312
#SPJ11
help i don't understand

Answers
Answer:
x = mn+y
Step-by-step explanation:
=> \(m = \frac{x-y}{n}\)
Multiplying n to both sides
=> x-y = mn
Now, Adding y to both sides
=> x = mn+y
Answer:
x = m n + y
Step-by-step explanation:
solve the system of equations by the addition method3x - 7y = 45x - 5y = 4
Answers
Set up but DO NOT evaluate a definite integral to find the area that represents the area of the region R inside the circle r=6cosθ and outside the curve r=9−6cosθ. The area can be found by evaluating ∫∣dθ (enter θ by typing the word "theta")
Answers
The integral to find the area of the region R is:
A = 2∫[9 - 12cosθ]dθ from 0 to 0.7227
To find the area of the region R inside the circle r=6cosθ and outside the curve r=9−6cosθ, we need to set up an integral that integrates with respect to θ.
First, we need to find the values of θ where the two curves intersect.
Setting the two equations equal to each other, we have:
6cosθ = 9 - 6cosθ
12cosθ = 9
cosθ = 3/4
Taking the inverse cosine of both sides, we have:
θ = ±0.7227
Since the curves are symmetric about the y-axis, we only need to consider the region in the first quadrant. Therefore, we can set up the integral as:
A = 2∫[r(θ)]dθ from 0 to 0.7227
where r(θ) is the equation of the outer curve minus the equation of the inner curve:
r(θ) = (9 - 6cosθ) - 6cosθ
r(θ) = 9 - 12cosθ
Therefore, the integral to find the area of the region R is:
A = 2∫[9 - 12cosθ]dθ from 0 to 0.7227
Note that we multiply the integral by 2 because we are only considering the first quadrant and need to account for the full area of the region R. However, we do not evaluate the integral as per the question prompt.
To know more about integrals refer here:
https://brainly.com/question/29093298#
#SPJ11
The definite integral for the enclosed area can be found by determining the limits of theta where the two functions intersect. Then, set up an integral that represents the absolute value of the difference in the radii of the two curves with respect to theta.
Explanation:The student is required to set up the definite integral for the area enclosed by two curves in polar coordinates. The curves are r=6cosθ and r=9−6cosθ.
Firstly, find the intersection points of these two curves which will give the limits of theta, by setting the two equations equal to each other: 6cosθ = 9 - 6cosθ. Then, construct the integral in the form of ∫∣f(θ)-g(θ)∣dθ where f(θ) and g(θ) represent the two given functions in order of their position in the given region R.
Learn more about Definite Integral here:https://brainly.com/question/32963975
#SPJ12
The sum of three consecutive odd integers is 75 . Find the value of the middle of the three.
Answers
The value of the middle of the three is 25.
Let x be the first odd integer, then the next two consecutive odd integers are x+2 and x+4. The sum of these three consecutive odd integers is given as 75, so we can write the equation:
x + (x+2) + (x+4) = 75
Simplifying the left side of this equation gives:
3x + 6 = 75
Subtracting 6 from both sides gives:
3x = 69
Dividing by 3 gives:
x = 23
So the first odd integer is 23, and the next two consecutive odd integers are 25 and 27. The middle of these three is the second consecutive odd integer, which is 25. Therefore, the value of the middle of the three is 25.
Learn more about value from
https://brainly.com/question/24078844
#SPJ11
e) Explain the approach you would take to verify that the following equation is an identity and why you would choose that approach. Do not actually verify that the equation is an identity.
(sin(x) + cos(x))² / sin(2x)= csc (2x) + 1
Answers
See below for the proof of the trigonometry identity
The approach to takeThe identity is given as:
(sin(x) + cos(x))² / sin(2x)= csc (2x) + 1
Start by expanding the numerator
(sin²(x) + cos²(x) + sin(2x)) / sin(2x)= csc (2x) + 1
Express sin²(x) + cos²(x) as 1
(1 + sin(2x)) / sin(2x)= csc (2x) + 1
Expand the fraction
1/sin(2x) + sin(2x)/sin(2x) = csc(2x) + 1
Evaluate the quotient
csc(2x) + 1 = csc(2x) + 1
Hence, the trigonometry identity has been proved
Read more about trigonometry identity at
https://brainly.com/question/63577
#SPJ1