¿En que orden se deben escribir las funciones, para aplicar la integral definida cuando se desea calcular el área?
Answers
Answer:
Si querés calcular el área entre las funciones f(x) y g(x) en el rango (a, b), usualmente se calcula la integral de la función más grande en el intervalo menos la función más pequeña en el intervalo, es decir, si:
f(x) > g(x) para todo x ∈ (a, b)
Entonces calculamos:
\(\int\limits^b_a {(f(x) - g(x))} \, dx\)
Puesto que el área se define como la encerrada por las dos curvas, y si lo hiciéramos de otro modo, las curvas no encerrarían ningun área.
Ahora, si no se cumple lo anterior, es decir, g(x) > f(x) en algún dado intervalo, entonces separamos la integral en distintas partes de tal forma que siempre definamos un área positiva.
es decir, si:
f(x) ≥ g(x) para x ∈ (a, n)
g(x) ≥ f(x) para x ∈ (n, b)
entonces el área estará dada por:
\(\int\limits^n_a {f(x) - g(x)}dx \, +\int\limits^b_n {g(x) - f(x)} \, dx\)
Related Questions
WILL GIVE BRAINLIEST AND 25 POINTS! Which of the following statements are true? Check all that apply. A. If any row of a square matrix is zero, its determinant is zero. B. If all numbers in a matrix are equal, its determinant is zero. C. The determinant of any identity matrix is zero. D. The determinant of a matrix with all positive numbers is always positive. E. The determinant of any zero matrix is zero.
Answers
Answer:
Option A, B and E
Step-by-step explanation:
Determinant = ad-bc
Let's look at the picture and solve all
Option A)
If the row ( c and d ) is zero, the determinant will be zero
=> a(0)-b(0)
=> 0-0
=> 0 (So, True)
Option B)
If a = b = c = d (Let's say 1), the determinant will be
=> (1)(1)-(1)(1)
=> 1-1
=> 0 (So, True)
Option C)
An Identity matrix is
=> \(\left[\begin{array}{ccc}1&0\\0&1\end{array}\right]\)
So , it's determinant will be
=> (1)(1)-(0)(0)
=> 1-0
=> 1 (So, False)
Option D)
The determinant with matrix will all positive numbers can be negative as well as positive. This is not necessary that it would be positive. (So, False)
Option E)
A zero matrix is
=> \(\left[\begin{array}{ccc}0&0\\0&0\end{array}\right]\)
So, it's determinant is:
=> (0)(0)-(0)(0)
=> 0-0
=> 0 (So,True)

Answer: A B E
A. If any row of a square matrix is zero, its determinant is zero.
B. If all numbers in a matrix are equal, its determinant is zero.
E. The determinant of any zero matrix is zero
Step-by-step explanation:
edge assignment
Guys, someone got it wrong. Were back at 56..Please give me the correct answer, guys.

Answers
Answer:
8 + 6 = 14
14 x 4 = 56
56 x 1/2(basically just dividing by 2) = 28 mm2
Formula of area of a trapezoid:
B1(base 1) + B2(base 2) x H(height) x 1/2(basically just dividing by 2)
In this case, 8 is your base your other base is 6 and your height is 4.
can someone please help me I asked my teacher for help but they won't answer me.PLEASE

Answers
We have a kyte and we have to find the measures of x and y.
As the line KM is the axis of symmetry, the angle TJM is congruent with the angle TLM, that has the measure y.
So y is also the measure of angle TJM, that has a measure of 52 degrees,
Then y = 52 degrees.
To find x, we use the fact that the sum of the angles of a triangle is equal to 180 degrees. The angle at vertex L is y and the angle at vertex T is a right angle (90 degrees).
Then, for triangle TLM, we have:
\(\begin{gathered} m\angle L+m\angle T+m\angle M=180\degree \\ y+90+x=180 \\ x=180-90-y \\ x=90-y \\ x=90-52 \\ x=38\degree \end{gathered}\)Answer:
x = 38 degrees.
y = 52 degrees.
I am so sorry if you keep seeing me ask for help

Answers
Answer:
67°-------------------
Given three interior angle measures of a triangle:
38°, 75° and xUse the triangle sum theorem to find the missing angle:
38 + 75 + x = 180x + 113 = 180x = 180 - 113x = 67So the missing angle is 67°.
A biochemical experiment involves combining together two protein extracts. Suppose a function φ(t) monitors the amount (nanograms) of extract A remaining at time t (nanoseconds). Assume you know these facts: 1. The function φ is invertible; i.e., it has an inverse function. 2. φ(0) = 6, φ(1) = 5, φ(2) = 3, φ(3) = 1, φ(4) = 0.5, φ(10) = 0.
(a) At what time do you know there will be 3 nanograms of extract A remaining?
(b) What is φ −1 (0.5) and what does it tell you?
(c) (True or False) There is exactly one time when the amount of extract A remaining is 4 nanograms.
(d) Calculate φ(φ−1 (1)) =
(e) Calculate φ−1 (φ(6)) =
(f) What is the domain and range of φ?
Answers
b) φ^(-1)(0.5) = 4 and it tells us that at t = 4 nanoseconds, there will be 0.5 nanograms of extract A remaining. This represents the inverse relationship between the amount of extract A remaining and time.
(c) False. Based on the given facts, there is no specific time mentioned when the amount of extract A remaining is exactly 4 nanograms. The known data points do not include φ(t) = 4.
(d) To calculate φ(φ^(-1)(1)), we substitute φ^(-1)(1) into the function φ. Since φ^(-1)(1) = 3, we evaluate φ(3). The result is φ(3) = 1, which means that at t = 3 nanoseconds, there will be 1 nanogram of extract A remaining.
(e) To calculate φ^(-1)(φ(6)), we substitute φ(6) into the inverse function φ^(-1). Since φ(6) = 0, we evaluate φ^(-1)(0). The result is φ^(-1)(0) = 10, indicating that at t = 10 nanoseconds, there will be 0 nanograms (or none) of extract A remaining.
(f) The domain of the function φ is the set of possible values for time t, which can range from 0 to a positive value, based on the experiment's time frame. The range of the function φ is the set of possible values for the amount of extract A remaining, which can range from 0 to 6 nanograms, based on the given facts.
Learn more about inverse functions and their properties here:
brainly.com/question/30338585
#SPJ11
The hypotenuse of a right triangle is 25 inches. The sine of one of the acute angles is 24/25. Which represents the
cosine for the other acute angle?
Answers
7 inches
[25]^2-(24)^2=49
Г49=7
The cosine for the other acute angle will be 7 / 25.
What is trigonometry?Trigonometric functions examine the interaction between the dimensions and angles of a triangular form.
The hypotenuse of a right triangle is 25 inches. The sine of one of the acute angles is 24/25.
sin θ = 24 / 25
We know that the sum of square of the sine and cosine of the angle will be equal to one. That is given as,
sin² θ + cos² θ = 1
Then the cosine for the other acute angle will be given as,
sin² θ + cos² θ = 1
(24 / 25)² + cos² θ = 1
576 / 625 + cos² θ = 1
cos² θ = 1 - 576 / 625
cos² θ = 49 / 625
cos² θ = (7 / 25)²
cos θ = 7 / 25
The cosine for the other acute angle will be 7 / 25.
More about the trigonometry link is given below.
https://brainly.com/question/22698523
#SPJ2
FILL THE BLANK. in an instruction like: z = x y, the symbols x, y, and z are examples of _____.
Answers
In an instruction like "z = x y," the symbols x, y, and z are examples of variables.
Variables are placeholders that represent unknown or changing values in mathematical expressions or equations. They allow us to generalize mathematical relationships and solve problems using algebraic methods.
In mathematics, variables are symbols that represent unknown or varying quantities. They are used to express mathematical relationships, equations, and formulas.
In the given instruction "z = x y," the symbols x, y, and z are variables.
In this case, x and y represent the input values, and z represents the output or result of the mathematical operation defined by the equation.
Variables are used extensively in algebra to solve equations, manipulate expressions, and analyze mathematical relationships. They enable us to express and solve problems symbolically, without knowing the specific values of the variables.
By assigning specific values to variables, we can evaluate expressions, solve equations, and find solutions to mathematical problems.
Variables can represent a wide range of quantities, including numbers, measurements, constants, or even abstract concepts. They provide flexibility and generality in mathematical modeling and problem-solving.
By using variables, we can establish connections between different mathematical quantities and derive meaningful conclusions based on their relationships.
Learn more about mathematical expressions here:
https://brainly.com/question/30350742
#SPJ11
Given the right triangle, evaluate: sin 0.

Answers
Answer: B. 5/13
This is the same as writing \(\frac{5}{13}\)
==========================================================
Reason:
We have two given sides of this right triangle. Use the pythagorean theorem to find the missing side.
a = 5 and b = 12 are the two known legs; c is the unknown hypotenuse
\(a^2+b^2 = c^2\\\\c = \sqrt{a^2+b^2}\\\\c = \sqrt{5^2+12^2}\\\\c = \sqrt{25+144}\\\\c = \sqrt{169}\\\\c = 13\\\\\)
The hypotenuse is exactly 13 units long. This is a 5-12-13 right triangle.
Now we can compute sine of theta
\(\sin(\text{angle}) = \frac{\text{opposite}}{\text{hypotenuse}}\\\\\sin(\theta) = \frac{5}{13}\\\\\)
This points us to choice B as the final answer.
----------------
Extra Info (optional)
5/12 is the value of tan(theta) since it's opposite/adjacent12/5 is the value of cot(theta), the reciprocal of tangent12/13 is the value of cos(theta), because cos = adjacent/hypotenuseName the polygon. Write whether it is regular
or not regular.

Answers
Answer:
it is an octagon; it is not regular
Which of the following is equivalent to the expression below?
3(5-2i)
Answers
Answer: 15 - 6i
Step-by-step explanation:
3(5-2i)
3×5+3×(−2i)
Do the multiplications.
15−6i
For an m×n matrix A, we define a matrix 1-norm as follows: ∥A∥ 1
=max 1≤j≤n
∑ i=1
m
∣a ij
∣. Make your own R function that returns the matrix 1-norm of a matrix. Test your code using the following matrix, A= ⎝
⎛
1
−2
−10
2
7
3
−5
0
−2
⎠
⎞
Answers
The R function provided calculates the 1-norm of an m×n matrix by summing the absolute values of each column and returning the maximum sum. It was tested with a specific matrix, resulting in a 1-norm value of 15.
Here's an R function that calculates the 1-norm of a given matrix:
```R
matrix_1_norm <- function(A) {
num_cols <- ncol(A)
norms <- apply(A, 2, function(col) sum(abs(col)))
max_norm <- max(norms)
return(max_norm)
}
# Test the function
A <- matrix(c(1, -2, -10, 2, 7, 3, -5, 0, -2), nrow = 3, ncol = 3, byrow = TRUE)
result <- matrix_1_norm(A)
print(result)
```
The function `matrix_1_norm` takes a matrix `A` as input and calculates the 1-norm by iterating over each column, summing the absolute values of its elements, and storing the column norms in the `norms` vector.
Finally, it returns the maximum value from the `norms` vector as the 1-norm of the matrix.
In the given example, the function is called with matrix `A` and the result is printed. You should see the output:
```
[1] 15
```
This means that the 1-norm of matrix `A` is 15.
To know more about matrix refer here:
https://brainly.com/question/33187423#
#SPJ11
PLEASE HELP!! HURRY!!

Answers
Answer:
B
Step-by-step explanation:
Its the second one, Answer B
Let V be a finite dimensional vector space dimensional and U C V is a subspace of V. Prove or disprove the following statement:
"If U and invariant under every linear operator on V, then U = {0} or U = V."
Answers
The statement "If U is invariant under every linear operator on V, then U = {0} or U = V" is false.
To prove or disprove the statement: "If U is invariant under every linear operator on V, then U = {0} or U = V," we need to examine the properties of invariant subspaces.
Let's consider the two cases:
Case 1: U = {0}
If U is the zero subspace, then it is trivially true that U = {0}.
Case 2: U = V
If U is the entire vector space V, then it is also true that U = V.
Now we need to consider whether there can be any other nontrivial invariant subspaces besides {0} and V.
To disprove the statement, we need to find a counterexample where U is a nontrivial invariant subspace of V.
Consider the following counterexample:
Let V be a two-dimensional vector space spanned by the basis vectors {v₁, v₂}. Let U be a subspace of V spanned by only one of the basis vectors, say U = span{v₁}.
Now, let's define a linear operator T on V such that T(v₁) = v₁ and T(v₂) = 0.
It is clear that U is invariant under the linear operator T since T(v₁) ∈ U for any v₁ ∈ U.
However, U ≠ {0} and U ≠ V in this case. Therefore, the statement "If U is invariant under every linear operator on V, then U = {0} or U = V" is false.
Hence, we have disproven the statement by providing a counterexample.
for such more question on linear operator
https://brainly.com/question/19803308
#SPJ8
A car travels 120m along a straight road that is inclined at 8° to the horizontal. Calculate the vertical distance through which the car rises. (Sin8°=0.1392)
Answers
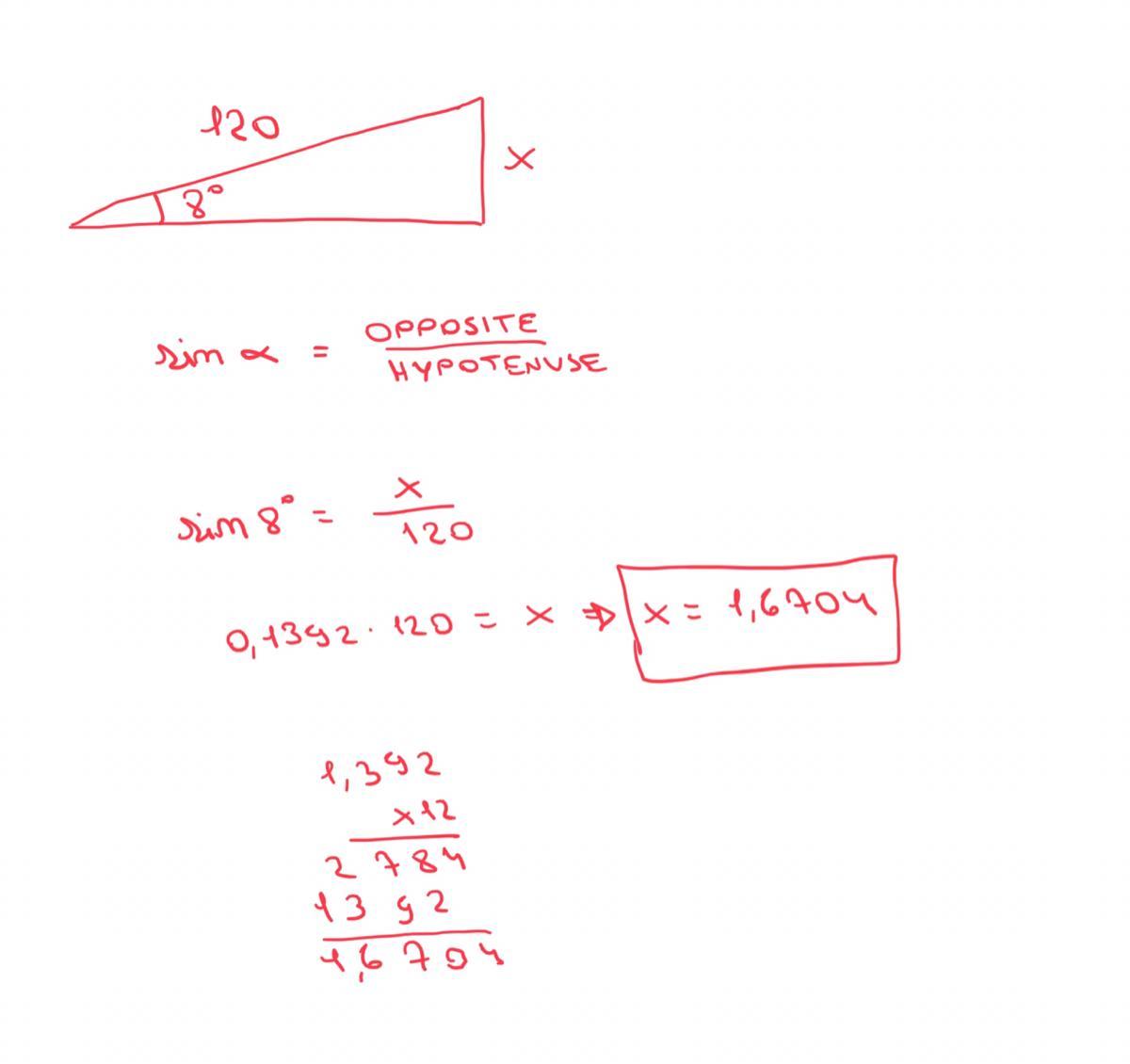
The vertical distance through which the car rises is 16.7 m
What is right triangle?"It is a triangle whose one of the angle is 90°."
What is sine of angle?In right triangle, for angle 'x',
sin(x) = (opposite side of angle x)/hypotenuse
For given example,
Consider the following figure for given situation.
A car travels 120 m along AC.
ΔABC is right triangle with hypotenuse AC.
∠C = 8°
Consider sine of angle C,
\(\Rightarrow sin(C)=\frac{AB}{AC}\\\\\Rightarrow sin(8^{\circ})=\frac{AB}{120}\\\\ \Rightarrow 0.1392=\frac{AB}{120}\\\\ \Rightarrow AB = 0.1392\times 120\\\\\Rightarrow AB = 16.70~ m\)
Therefore, the vertical distance through which the car rises is 16.7 m
Learn more the sine angle here:
https://brainly.com/question/14553765
#SPJ2

A square has vertices at (1,1), and (2, -1). Where are the two vertices located? How do you know you have created a square?

Answers
If you graph the point
(1,1)
and
(2,-1)
you see this. Shown below:
Here are some letters and what they represent. All costs are in dollars. m represents the cost of a main dish. n represents the number of side dishes. s represents the cost of a side dish. t represents the total cost of a meal. Discuss with a partner: What does each equation mean in this situation? a. M = 7.50
Answers
The given question is incomplete
Here are some letters and what they represent. All costs are in dollars.
m represents the cost of a main dish.
n represents the number of side dishes.
s represents the cost of a side dish.
t represents the total cost of a meal.
Discuss with a partner: What does each equation mean in this situation? a. a. m = 7.50
b. m = s + 4.50
c . ns = 6
d. m + ns = t
2. Write a new equation that could be true in this situation.
Answer:
t = 3m -n(s+1)
Step-by-step explanation:
Using the information we can describe the value of each letters
using a and b
we have m = 7.50 and m = s + 4.507.50 = s + 4.50
s = 3
substitute s in c, we get
ns = 6n = 6/3 = 2using equation d we have
m + ns = t7.50 + 6 = tt = 13.50so we an equation using the above data
t +ns = 3m - n
t = 3m -n(s+1)
You decide to make 10 lb of a peanut-and-raisin mixture to sell at the class snack sale. You can buy peanuts for $2.50 per pound and raisins for $1.75 per pound. If you want to sell the mixture for $2 per pound, how many pounds of peanuts and how many pounds of raisins should you use
Answers
On solving the provided question, we can say that by linear equation 10/3 pounds of peanuts and how many pounds of raisins should you use.
What is a linear equation?A linear equation is one that has the form y=mx+b in algebra. B is the slope, and m is the y-intercept. It's usual to refer to the previous clause as a "linear equation with two variables" because y and x are variables. The two-variable linear equations known as bivariate linear equations. There are several instances of linear equations: 2x - 3 = 0, 2y = 8, m + 1 = 0, x/2 = 3, x + y = 2, and 3x - y + z = 3. It is referred to as being linear when an equation has the form y=mx+b, where m stands for the slope and b for the y-intercept.When an equation has the formula y=mx+b, with m denoting the slope and b the y-intercept, it is referred to as being linear.
here,
the linear equation that is formed is
10p +7 (10 - p) = 80
10p + 70 - 7p = 80
3p = 70
p = 10/3
10/3 pounds of peanuts and how many pounds of raisins should you use
To know more about linear equation visit:
https://brainly.com/question/11897796
#SPJ4
someone please help me, I’m struggling :(

Answers
Answer:
constant because it isn't going up or down, just moving straight
Step-by-step explanation:
Answer:
constant
Step-by-step explanation:
Since this is a horizontal line the slope is zero
This means the graph is constant
What does it mean for two polynomials to be closed? How do you add/subtract polynomials?
Answers
what percentage of students earned A’s on their paper ?

Answers
Answer:
21% or C
Step-by-step explanation:
If 60 students either didn't pass, got Cs or Bs, then 16 out of the 76 got As which is 21 percent.
Using Table H, find the P-value interval for a right-tailed test when F = 2.97, d.f.N. - =
9, and d.f.D. = 14.
O 0.005 P-value < 0.01
O 0.01 P-value < 0.025
O 0.025 P-value < 0.05
O 0.05 P-value < 0.1
Answers
The correct answer is:
0.025 P-value < 0.05
In statistical hypothesis testing, the P-value is a measure of the strength of evidence against the null hypothesis. It represents the probability of observing a test statistic as extreme as the one calculated from the sample data, assuming the null hypothesis is true.
In this case, we have a right-tailed test, which means we are interested in the upper tail of the F-distribution. The test statistic is calculated as F = 2.97, with degrees of freedom for the numerator (d.f.N.) = 9 and degrees of freedom for the denominator (d.f.D.) = 14.
Using Table H (which provides critical values for the F-distribution), we can determine the P-value interval. In this table, we find the column for d.f.N. = 9 and locate the row that corresponds to d.f.D. = 14. The intersection of these values gives us the critical value, which is 0.025.
Since the F-value of 2.97 is greater than the critical value of 0.025, the P-value is less than 0.05. Therefore, we can conclude that 0.025 < P-value < 0.05, indicating strong evidence against the null hypothesis.
Learn more about P-value:
https://brainly.com/question/13786078
#SPJ11
Jim is making salsa recipe calls for 3 1/3 cups of tomato sauce for every 1/6 cups of the cilantro if Jim has one cup of cilantro how many cups of tomato sauce with he need 
Answers
Jim will need 20 cups of tomato sauce.
what is the probability, to the nearest hundredth, that a point chosen randomly inside the rectangle is in the triangle?
Answers
The probability that a point chosen randomly inside the rectangle is in the triangle is 1/3, or approximately 0.33 to the nearest hundredth.
The probability that a point chosen randomly inside the rectangle is in the triangle is equal to the area of the triangle divided by the area of the rectangle.
To find the area of the triangle, we need to first find its base and height. The base of the triangle is the length of the rectangle, which is 8 units. To find the height, we need to draw a perpendicular line from the top of the rectangle to the base of the triangle. This line has a length of 4 units. Therefore, the area of the triangle is (1/2) x base x height = (1/2) x 8 x 4 = 16 square units.
The area of the rectangle is simply the length times the width, which is 8 x 6 = 48 square units.
Therefore, the probability that a point chosen randomly inside the rectangle is in the triangle is 16/48, which simplifies to 1/3.
In conclusion, the probability that a point chosen randomly inside the rectangle is in the triangle is 1/3, or approximately 0.33 to the nearest hundredth.
To know more about probability visit:
brainly.com/question/31828911
#SPJ11
Please help me respond this

Answers
Option 2 is correct that is 1.79
What is third quartile ?When presented in ascending order, the value that 75% of data points fall within is known as the higher quartile, or third quartile (Q3).
The quartiles formula is as follows:
Upper Quartile (Q3) = 3/4(N+1)
Lower Quartile (Q1) = (N+1) * 1/3
Middle Quartile (Q2) = (N+1) * 2/3
Interquartile Range = Q3 -Q1,
1.74, 0.24, 1.56, 2.79, 0.89, 1.16, 0.20, and 1.84 are available.
Sort the data as follows: 0.20, 0.24, 0.89, 1.16, 1.56, 1.74, 1.84, 2.79 in ascending order of magnitude.
The data set has 8 values.
hence, n = 8; third quartile: 3/4 (n+1)th term
Q3 =3/4 of a term (9) term
Q3 =27/4 th term
Q3 = 1.74 + 1.84 / 2 (average of the sixth and seventh terms)
equals 1.76
Thus Q3 is 1.76 that is option 2
To know more about third quartile click the link:
brainly.com/question/24329548
#SPJ1
If there is a bag with the numbers
in it and you draw
out numbers, without replacing them, how
many different combinations can you make?
Group of answer choices
120
125
3
60
Answers
There are 84 different combinations that can be made when drawing 3 numbers from a set of 9 numbers without replacement.
The Combinations is used to calculate the number of ways you can select a certain number of items from a larger set, without regard to their order. In other words, combinations focus on the selection of items rather than their arrangement.
When drawing 3 numbers from a set of 9 numbers without replacement, the number of different combinations can be calculated using concept of combinations.
The total-number of items (n) = 9, and r is the number of items selected (3 in this case). Using this formula, the number of combinations is:
⁹C₃ = 9!/(3!(9-3)!) = 84,
Therefore, there are 84 different combinations.
Learn more about Combination here
https://brainly.com/question/3204685
#SPJ4
The given question is incomplete, the complete question is
If there is a bag with the numbers 1 to 9 in it and you draw out 3 numbers, without replacing them, how many different combinations can you make?
5. Seven more than three times a number is twenty-five.
Answers
Answer:
let the number be x
then, 3x + 7= 25
3x=18
x=6 so number is 6 and ewiation is 3x+7=25
Answer:
The number is 6
Step-by-step explanation:
Let x be the number
3x+7 = 25
Subtract 7 from each side
3x+7-7= 25-7
3x = 18
Divide by 3
3x/3 =18/3
x=6
A farm has 14 cows and 10 horses. Write the
ratio of cows to horses as a fraction in lowest
terms.
Answers
Answer: 7:5
Step-by-step explanation: 14/2 = 7 and 10/2 = 5
I am truly sorry if it was wrong or i did not understand ty.
- ♥ Roxy ♥
You buy a car for $22,000 and every year your car depreciates by 14% (in other words, you car decreases in value by 14% every year). What is your car worth in 4 years?
(Create an exponential function to solve this problem.)
Question options:
$18,920
$37,157
$12,034
$25,080
Answers
$12034 is the worth of the car after 4 years.
What is Percentage?Percentage, a relative value indicating hundredth parts of any quantity.
Given that we purchased a car for $22,000
Every year your car depreciates by 14%
We have to find the worth of the car after 4 years.
\(A=P(1-r)^{t}\)
P is the principal amount=$12000
r is rate of interest =14%=0.14
t is time =4 years
A=22000(1-0.14)⁴
A=22000(0.86)⁴
A=22000×0.547
A=$12034
Hence, $12034 is the worth of the car after 4 years.
To learn more on Percentage click:
https://brainly.com/question/28269290
#SPJ1
in a sample of 20 men, the mean height was 178 cm. in a sample of 30 women, the mean height was 164 cm. what was the mean height for b oth groups put together?
Answers
In a sample of 20 men, the mean height was 178 cm and a sample of 30 women, the mean height was 164 cm, then the mean height for both groups combined is approximately 172.4 cm.
To find the mean height for both groups combined, we need to calculate the weighted average of the means of each group, where the weight of each group is proportional to its sample size.
We can begin by finding the total height of all the individuals in both groups combined. The total height for the men's group would be 20 multiplied by the mean height of 178 cm, which is 3560 cm.
Similarly, the total height for the women's group would be 30 multiplied by the mean height of 164 cm, which is 4920 cm. Adding these two values gives a total height of 8480 cm for both groups combined.
Next, we need to find the total sample size, which is the sum of the sample sizes of the two groups. The total sample size is 20 + 30 = 50.
Finally, we can calculate the weighted average of the means of each group using the formula:
Weighted average = (weight of group 1 * mean of group 1 + weight of group 2 * mean of group 2) / (weight of group 1 + weight of group 2)
In this case, the weights of each group are proportional to their sample sizes. Therefore, the weighted average can be calculated as:
Weighted average = (20/50 * 178 cm) + (30/50 * 164 cm) = 172.4 cm
In summary, to find the mean height for both groups combined, we need to calculate the weighted average of the means of each group, where the weight of each group is proportional to its sample size. This is done by multiplying the sample size of each group by its mean height, adding the values, and then dividing by the total sample size.
To learn more about mean click on,
https://brainly.com/question/3699952
#SPJ4
chegg multiple regression is an extension of- a) bayesian linear regression. b) logistic regression. c) simple linear regression. d) polynomial regression.
Answers
The answer to your question is c) simple linear regression. Chegg multiple regression is an extension of simple linear regression.
Multiple regression involves using multiple predictor variables to predict the value of a dependent variable. In simple linear regression, there is only one predictor variable.
In multiple regression, there are two or more predictor variables. The main answer to your question is c) simple linear regression.
In simple linear regression, a single independent variable is used to predict the value of a dependent variable.
Multiple regression extends this concept by allowing for the use of multiple independent variables. Multiple regression allows for more complex relationships between the independent and dependent variables to be explored.
To summarize, Chegg multiple regression is an extension of simple linear regression and allows for the use of multiple predictor variables to predict the value of a dependent variable.
To know more about Multiple regression visit:
brainly.com/question/31389527
#SPJ11