Answers
Answer:
1. 52
2. 86
3. 55
Answer:
if its so easy, why cant you do it?
Step-by-step explanation:
but either way its
52
86
55
Related Questions
What is the equation of the blue line?
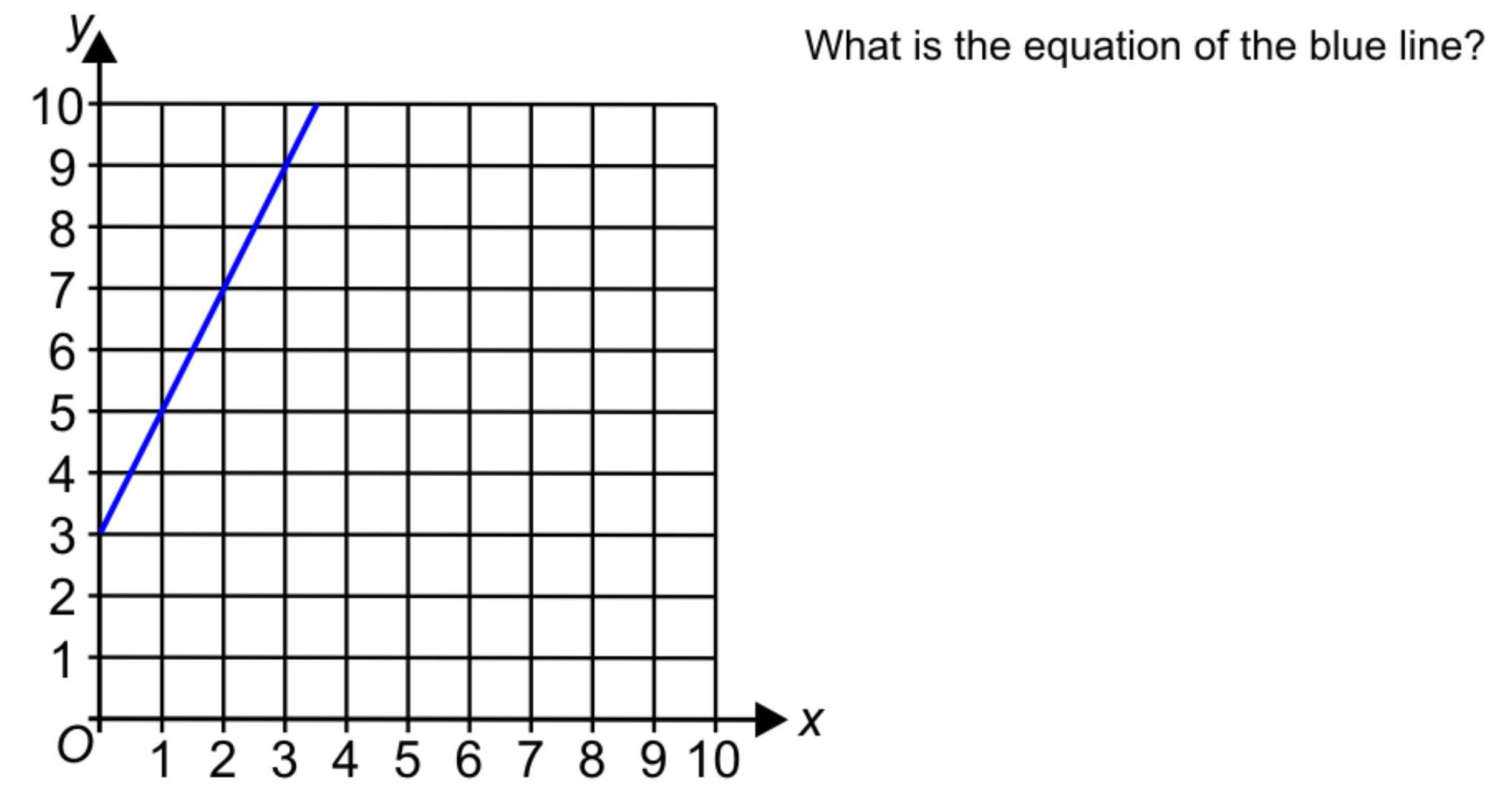
Answers
Answer:
y=2x+3
Step-by-step explanation:
The equation of a line is:
\(y=mx+b\) with m being the slope and b being the y-intercept.
The slope is \(\frac{rise}{run}\), where rise is how many units you go up/down from one point to another, and the run is how many units you go left/right from one point to another.
The y-intercept is when x=0, or where the line intercepts the y-axis.
In this case, we can see that the blue line intercepts the y-axis at (0,3), making 3 our y-intercept.
To find the slope, we first have to choose 2 points. Let's choose (0,3) and (1,5).
We can see that to go from (0,3) to (1,5), we have to go up 2 units and go right 1 unit. This means our slope is 2/1, or 2.
So, we can substitute the y-intercept and slope into our formula:
y=2x+3
Hope this helps! :)
Picture below has question/answer choices!!


Answers
The statements that is true about the similarity of the two triangles the option D
D. ΔMNO and ΔJKL are not similar triangles
What are similar triangles?Similar triangles are triangles which have proportional corresponding sides
The parameters in the question are;
The length of segment MN = 20
Length of segment NO = 12
Length of segment OM = 25
Measure of angle ∠O = 56°
Length of segment LJ =- 15
Length of segment JK = 12
Length of segment KL = 9
Measure of angle ∠L = 56°
Two triangles are similar if the ratio of two sides on one triangle are proportional to two sides of another triangle, and the included angle between the two sides are congruent
The included angle between sides ON and MO on triangle MNO is congruent to the included angle between segment LK and JL in triangle JKL
However, the ratio of the sides LK to ON and JL to MO are;
9/12 ≠ 15/25
Therefore, the triangles are not similar
The correct option is option D
Learn more about similar triangles here:
https://brainly.com/question/2644832
#SPJ1
what is the equation of the line in slope-intercept form?

Answers
The linear function for this problem is defined as follows:
y = x + 50.
How to define a linear function?The slope-intercept equation for a linear function is presented as follows:
y = mx + b
In which:
m is the slope.b is the y-intercept.The graph touches the y-axis at y = 50, hence the intercept b is given as follows:
b = 50.
When x increases by 10, y also increases by 10, hence the slope m is given as follows:
m = 10/10
m = 1.
Hence the function is given as follows:
y = x + 50.
More can be learned about linear functions at https://brainly.com/question/15602982
#SPJ1
What is an equation that is equivalent to -3/4x+1/8=-3/8?
Also the / is not a division symbol. The numbers with a / are fractions.
Answers
Hope this helps! Follow my Instagram trlamb822!

Solve this please! Will give correct answer brainiest!

Answers
Answer:
it is $5 per hour
Answer:
It is c.
Step-by-step explanation:
Divide the amount earned by hours. For example 10/2=5, 20/4=5, 30/6=5 and so on
n a survey, the ratio of students who prefer muffins to bagels is 4 to 5. if the number of students surveyed who prefer muffins is 420, how many prefer bagels?
Answers
If the ratio of students who prefer muffins to bagels is 4 to 5. if the number of students surveyed who prefer muffins is 420 then the number of students who prefer bagels is 21
Ratio: In mathematics the quantitative relation between two amounts showing the number of times one value contains or is contained within the other is known as ratio.
Given that,
The ratio of the students who prefer muffins to bagels is 4:5 means 4/5.
Number of students who prefer muffins is 420
Let, the number of students who prefer bagels is x
According to the question,
4a:5a = 420:x
⇒4a/5a = 420/x
⇒4/5 = 420/x
⇒x(4/5) = 420
⇒4x = 420×5
⇒4x = 84
⇒x = 21
Therefore the number of students who prefer bagels is 21
Learn more about ratio:
https://brainly.com/question/13513438
#SPJ4
Which property or postulate is shown? If A=B and B=C, then A=C.
Subtraction Postulate
Symmetric Property
Transitive Property
Reflexive Property
Answers
This is the transitive property :)
Find the possible coordinates of PI’m struggling to do the second part of this question and would like some assistance please

Answers
we have the equation of curve C
\(y=x^3-11x+1\)Part a
Find out the gradient, where x=3
To find the gradient, take the derivative of the function with respect to x, then substitute the x-coordinate of the point of interest for the x values in the derivative
so
the first derivative is equal to
\(y^{\prime}=3x^2-11\)Evaluate the first derivative for x=3
\(\begin{gathered} y^{\prime}=3(3^2)-11 \\ y^{\prime}=16 \end{gathered}\)the gradient is equal to 16Part b
we know that the gradient is equal to 1 at point P
so
equate the first derivative to 1
\(\begin{gathered} y^{\prime}=3x^2-11 \\ 3x^2-11=1 \\ 3x^2=12 \\ x^2=4 \\ x=\pm2 \end{gathered}\)Find out the possible y-coordinate of point P
For x=2
substitute in the given equation of C
\(\begin{gathered} y=2^3-11(2)+1 \\ y=8-22+1 \\ y=-13 \end{gathered}\)the first possible coordinate of P is (2,-13)For x=-2
\(\begin{gathered} y=-2^3-11(-2)+1 \\ y=-8+22+1 \\ y=15 \end{gathered}\)the second possible coordinate of P is (-2,13)segment ab is on the line y − 4 = −5(x − 1), and segment cd is on the line y − 4 = one fifth(x − 5). which statement proves the relationship of segments ab and cd?
Answers
The relationship between segments AB and CD is that they are perpendicular because they have slopes that are opposite reciprocals of -5 and 1/5.
Option B is the correct answer.
We have,
For segment AB, the equation of the line is y - 4 = -5(x - 1).
By rearranging this equation to the slope-intercept form (y = mx + b),
we get:
y = -5x + 5 + 4
y = -5x + 9
Comparing this with the general equation, we can see that the slope of segment AB is -5.
For segment CD, the equation of the line is y - 4 = 1/5(x - 5).
Again, rearranging to the slope-intercept form, we get:
y = 1/5 x + 1/5 * 5 + 4
y = 1/5 x + 1 + 4
y = 1/5 x + 5
Comparing this with the general equation, we can see that the slope of segment CD is 1/5.
Now,
The slopes are -5 and 1/5, respectively.
They are perpendicular because they have slopes that are opposite reciprocals of -5 and 1/5.
Therefore,
The relationship between segments AB and CD is that they are perpendicular because they have slopes that are opposite reciprocals of -5 and 1/5.
Learn more about the equation of a line here:
https://brainly.com/question/23087740
#SPJ12
The complete question.
Segment AB is on the line y − 4 = −5 (x − 1), and segment CD is on the line y − 4 = 1/5 (x − 5).
Which statement proves the relationship between segments AB and CD?
They are perpendicular because they have slopes that are opposite reciprocals of 5 and −1/5
They are perpendicular because they have slopes that are opposite reciprocals of -5 and 1/5.
They are parallel because they have the same slope of 5.
They are parallel because they have the same slope of −1/5.
Can someone help me with this please.

Answers
Answer: Rebate applied AFTER the discount
Step-by-step explanation:
Because the rebate value stays the same no matter what, but the discount doesn't.
its due today please help

Answers
Answer:
5
Step-by-step explanation:
Answer:
\( \boxed{0.76} \: is \: correct.\)
Step-by-step explanation:
\( let \: the \: unknown \: ounce \: be \to \: u_{kn}\\ if \: 1 \: ounce \: is = 23.8 \: grams \\ then \to \: u_{kn} = \frac{18 \: grams \times 1 \: ounce}{23.8 \: grams } \\ u_{kn} = \frac{18}{23.8} (1 \: ounce \:) = 0.756302521 \times 1 \: ounce \\ \boxed{u_{kn} = 0.756302521 \: ounce }\)
♨Rage♨
The average distance a swimmer swims
can be described by the equation
d= 30t, where d is the
horizontal
distance in meters and tis the time
in minutes. Find the distances the
swimmer swims at the times of 7, 10, 14,
and 20 minutes.
Answers
Answer:
the distance for 7 minutes is 210m
the distance for 10 minutes is 300m
the distance for 14 minutes is 420m
the distance for 29 minutes is 600m
Step-by-step explanation:
d=30(7)
d=210
d=30(10)
d=300
d=30(14)
d=420
d=30(20)
d=600
When x=-3, then y=______

Answers
Answer:-1
Step-by-step explanation:
Answer: -6
Step-by-step explanation:
the line pass through (-3,-6)
6sin^2 (x) + 6sin (x) + 1 = 0
solve and show steps for the graph ( i already have the graph )
Answers
To solve the equation \(6sin^2(x)\) + 6sin(x) + 1 = 0, we can use algebraic methods and the unit circle to determine the values of x that satisfy the equation.
1. Start by rearranging the equation to a quadratic form: \(6sin^2(x)\) + 6sin(x) + 1 = 0.
2. Notice that the equation resembles a quadratic equation in terms of sin(x). Let's substitute sin(x) with a variable, such as u: \(6u^2\) + 6u + 1 = 0.
3. Solve this quadratic equation for u. You can use the quadratic formula or factorization methods to find the values of u. The solutions are u = (-3 ± √3) / 6.
4. Since sin(x) = u, substitute back the values of u into sin(x) to obtain the values for sin(x): sin(x) = (-3 ± √3) / 6.
5. To find the values of x, we can use the inverse sine function. Take the inverse sine of both sides: x = arcsin[(-3 ± √3) / 6].
6. The arcsin function has a range of [-π/2, π/2], so the values of x lie within that range. Use a calculator to find the approximate values of x based on the values obtained in step 5.
7. Plot the obtained x-values on the graph to show the solutions of the equation \(6sin^2(x)\) + 6sin(x) + 1 = 0. The graph will illustrate the points where the curve intersects the x-axis.
For more such questions on algebraic, click on:
https://brainly.com/question/4344214
#SPJ8
Two buses leave Chicago at the same time traveling in opposite directions. One bus travels at54 mph and the other at63 mph. How soon will they be234 miles apart?
Answers
First, combine there speed
speed = 54 + 63 =117 mph
Distance given = 234 miles
Speed = distance / time
This implies that;
time = distance / speed
=234 / 117
= 2hours
In 2 hours, they will be 234 miles apart
The System of PolynomialsYou are aware of the different types of numbers: natural numbers, integers, rational numbers, and real numbers. Now you will work with a property of the number system called the closure property. A set of numbers is closed for a specific mathematical operation if you can perform the operation on any two elements in the set and always get a result that is an element of the set.Consider the set of natural numbers. When you add two natural numbers, you will always get a natural number. For example, 3 + 4 = 7. So, the set of natural numbers is said to be closed under the operation of addition.Similarly, adding two integers or two rational numbers or two real numbers always produces an integer, or rational number, or a real number, respectively. So, all the systems of numbers are closed under the operation of addition.Think of polynomials as a system. For each of the following operations, determine whether the system is closed under the operation. In each case, explain why it is closed or provide an example showing that it isn’t.1. AdditionType your response here:2. SubtractionType your response here:3. MultiplicationType your response here:4. DivisionType your response here:
Answers
Polynomials are closed under the operation of addition, subtraction, and multiplication only. Here's why:
1. Addition: (Closed)
Reason: Say we have two polynomials: (x⁴ + 2x³ - 4) and (3x³ - 2x² + 6x). If we add these two polynomials, (x⁴ + 2x³ - 4) + (3x³ - 2x² + 6x), it will result to x⁴ + 5x³ - 2x² + 6x - 4 which is also a polynomial.
When adding polynomials, the variables and the exponents don't change. This guarantees that the sum of these variables with exponents will always be a polynomial.
2. Subtraction: (Closed)
Reason: Say we have two polynomials: (x⁴ + 2x³ - 4) and (3x³ - 2x² + 6x). If we subtract these two polynomials, (x⁴ + 2x³ - 4) - (3x³ - 2x² + 6x), it will result to x⁴ - x³ + 2x² - 6x - 4 which is also a polynomial.
When subtracting polynomials, the variables, and the exponents don't change. This guarantees that the difference of these variables with exponents will always be a polynomial.
3. Multiplication: (Closed)
Reason: Say we have two polynomials (x + 2) and (x - 4). If we multiply these two polynomials, (x + 2)(x - 4), it will result in x² - 2x - 8, which is also a polynomial.
When multiplying polynomials, the variables do not change but the exponents will be added to each other. In this case, we can guarantee that the new exponents will be positive whole numbers still and this guarantees that the answer will be a polynomial.
4. Division: (Not closed)
Reason: When dividing polynomials, exponents are being subtracted from each other, therefore, we might have a result of a negative exponent. Negative exponents are not allowed in a polynomial. Example, say we have two polynomials (x²) and (x⁴), if we divide (x²) by (x⁴), the resulting value would be:
\(\frac{x^2}{x^4}=x^{-2}\)The resulting value is x to the power of negative 2, and is not a polynomial.
Set up the partial fraction decomposition for a given function. Do not evaluate the coefficients. f(x) = (b) √ 16x3 +12r² + 10x +2 (x4-4x²)(x² + x + 1)²(x²-3x + 2)(x+3x²+2) 2. Evaluate the following indefinite integrals. Hint: All of the questions can be reduced to an integral of a rational function by using a proper substitution, or integration by parts. (a) dx. 3x²-3x+1 ³+1 1 2+e+e- x² + 2x + 5 x +4 dx. dx. +4 (d) √2+2x+5 (e) x. Tan¹(x) dx. dr.
Answers
Set up the partial fraction decomposition for the given function:
\($f(x)=\frac{(b)\sqrt{16x^3+12r^2+10x+2}}{(x^4-4x^2)(x^2+x+1)^2(x^2-3x+2)(x+3x^2+2)}$\)
is: \(=\frac{3}{26}x^2-\frac{21}{13}x+\frac{9}{13}\ln|x+4|-\frac{1}{13}\arctan\frac{x+1}{2}+\frac{5}{39}\ln[(x+1)^2+4]+C\)
The denominator factors completely to:
\(x^4-4x^2=x^2(x^2-4)=x^2(x-\sqrt{2})(x+\sqrt{2})\)
\(x^2+x+1=(x-(\frac{-1+i\sqrt{3}}{2}))(x-(\frac{-1-i\sqrt{3}}{2}))$$\)
\(x^2-3x+2=(x-2)(x-1)\)
\(x+3x^2+2=(x+\frac{3}{2})^2-\frac{1}{4}\)
Therefore,
\(\begin{aligned}\frac{f(x)}{(b)\sqrt{16x^3+12r^2+10x+2}}&=\frac{A}{x}+\frac{B}{x-\sqrt{2}}+\frac{C}{x+\sqrt{2}}+\frac{Dx+E}{x^2+x+1}+\frac{Fx+G}{(x^2+x+1)^2}\\&+\frac{H}{x-2}+\frac{J}{x-1}+\frac{Kx+L}{x+\frac{3}{2}+\frac{1}{2}}+\frac{Nx+M}{(x+\frac{3}{2}+\frac{1}{2})^2}\end{aligned}\)
(a) \($\int\frac{3x^2-3x+1}{(x^2+2x+5)(x+4)}dx$\) is
\($\frac{1}{13}\int\frac{3x^2-3x+1}{x+4}dx-\frac{1}{13}\int\frac{3x^2-3x+1}{x^2+2x+5}dx$\).
\(=\frac{3}{13}\int\frac{x^2-x}{x+4}dx+\frac{1}{13}\int\frac{1}{x+4}dx-\frac{1}{13}\int\frac{3x^2-3x+1}{(x+1)^2+4}dx\)
\(=\frac{3}{13}\int\frac{x^2-x}{x+4}dx+\frac{1}{13}\ln|x+4|-\frac{1}{39}\int\frac{3x-7}{(x+1)^2+4}d(x+1)\)
\(=\frac{3}{13}\int x-4+\frac{16}{x+4}dx+\frac{1}{13}\ln|x+4|-\frac{1}{39}\int\frac{3}{t^2+4}dt-\frac{1}{39}\int\frac{x+5}{(x+1)^2+4}d(x+1)\)
\(=\frac{3}{26}x^2-\frac{21}{13}x+\frac{9}{13}\ln|x+4|-\frac{1}{13}\arctan\frac{x+1}{2}+\frac{5}{39}\ln[(x+1)^2+4]+C\)
where t=x+1 is used. The answer is obtained by partial fraction decomposition and substitution. The value of the constant C is not given.
Conclusion: Partial fraction decomposition is a technique to decompose complex rational functions into simpler rational functions. In this technique, we decompose a complex rational function into simpler fractions whose denominators are linear factors or irreducible quadratic factors. This is the easiest way to solve integrals of rational functions that are complex.
To know more about visit fraction visit
https://brainly.com/question/25101057
#SPJ11
The partial fraction decomposition for the given function and evaluated the given indefinite integrals.
∫dx/[(3x²-3x+1)³+1] = -1/6[1/(3x² - 3x + 2)] + 1/6[1/[(3x² - 3x + 2)²]] + 1/2[arctan(6x² - 6x + 1)] + C
∫dx/[(x² + 2x + 5)(x + 4)] = 1/(x + 4) - 2x + 1/(x² + 2x + 5) + C
∫dx/√(2 + 2x + 5) = (1/2) ∫du/√u
The partial fraction decomposition for the given function and evaluated the given indefinite integrals.
The steps to set up the partial fraction decomposition for a given function
f(x) = (b) √ 16x³ +12r² + 10x +2 (x⁴-4x²)(x² + x + 1)²(x²-3x + 2)(x+3x²+2) are given below:
Step 1: Factorise the denominator: x⁴ - 4x² = x²(x² - 4)
= x²(x + 2)(x - 2) (x² + x + 1)²(x² - 3x + 2)(x + 3x² + 2)
Step 2: Determine the degree of the numerator, which is less than the degree of the denominator. In this case, the degree of the numerator is 1. So, the partial fraction decomposition will be of the form
A/x + B/(x² + x + 1) + C/(x² - 3x + 2) + D/(x + 3x² + 2) + E/[(x² + x + 1)²]
Step 3: Multiply the original function f(x) by the denominator, set the numerator of the result equal to the sum of the numerators of the partial fractions, and simplify. Then, equate the coefficients of the resulting polynomial equations in x with each other. Solve the system of equations for the unknown constants. Then, use partial fraction decomposition to break up a rational function into simpler fractions.
Explanation: Given function is f(x) = (b) √ 16x³ +12r² + 10x +2 (x⁴-4x²)(x² + x + 1)²(x²-3x + 2)(x+3x²+2). Partial fraction decomposition is the decomposition of a rational function into simpler fractions. The steps to set up the partial fraction decomposition for a given function f(x) = (b) √ 16x³ +12r² + 10x +2 (x⁴-4x²)(x² + x + 1)²(x²-3x + 2)(x+3x²+2) are as follows:
Step 1: Factorise the denominator: x⁴ - 4x² = x²(x² - 4) = x²(x + 2)(x - 2) (x² + x + 1)²(x² - 3x + 2)(x + 3x² + 2)
Step 2: Determine the degree of the numerator, which is less than the degree of the denominator. In this case, the degree of the numerator is 1. So, the partial fraction decomposition will be of the form A/x + B/(x² + x + 1) + C/(x² - 3x + 2) + D/(x + 3x² + 2) + E/[(x² + x + 1)²]
Step 3: Multiply the original function f(x) by the denominator, set the numerator of the result equal to the sum of the numerators of the partial fractions, and simplify. Then, equate the coefficients of the resulting polynomial equations in x with each other. Solve the system of equations for the unknown constants. Then, use partial fraction decomposition to break up a rational function into simpler fractions.
The answers for the given integrals are as follows:
(a) ∫dx/[(3x²-3x+1)³+1] = 1/3 ∫du/u³
(by substitution, let u = 3x² - 3x + 1)
= -1/6[1/(u² + u + 1)] + 1/6[1/[(u² + u + 1)²]] + 1/2[arctan(2u - 1)] + C
= -1/6[1/(3x² - 3x + 2)] + 1/6[1/[(3x² - 3x + 2)²]] + 1/2[arctan(6x² - 6x + 1)] + C
(b) ∫dx/[(x² + 2x + 5)(x + 4)] = A/(x² + 2x + 5) + B/(x + 4)
= [A(x + 4) + B(x² + 2x + 5)]/[(x² + 2x + 5)(x + 4)]
= [(A + B)x² + (4A + 2B)x + (5B)]/[(x² + 2x + 5)(x + 4)]
= 1/(x + 4) - 2x + 1/(x² + 2x + 5) + C
(d) ∫dx/√(2 + 2x + 5)
= ∫dx/√(7 + 2x) = (1/√2)arcsin((2x + 1)/√7) + C
(e) ∫xdx/(1 + x²) = (1/2)ln(1 + x²) + (1/2)arctan(x) + C(d) ∫dr/[(b) √ 16r³ + 12r² + 10r + 2]
= (1/2) ∫du/√u
(by substitution, let u = 16r³ + 12r² + 10r + 2)
= (1/2) √u + C
= (1/2) √(16r³ + 12r² + 10r + 2) + C.
Conclusion: Thus, we have set up the partial fraction decomposition for the given function and evaluated the given indefinite integrals.
To know more about integrals visit
https://brainly.com/question/31433890
#SPJ11
-4(-2x-9) I really need help it's simplify
Answers
Answer:
2x+9
Step-by-step explanation:
-4(-2x-9)
8x+36
2x+9
Hope u got it
If you have any question just ask me
If you think this the best answer please mark me as brainliest
Answer:
2x + 9
Step-by-step explanation:
-4(-2x-9)
^ first start with distributive property
8x + 36
^ and simplify
2x + 9
and you've got your expression!
let me know if you're confused on anything else
pls help i will give brainliest to the quickest correct answer
graph the line with slope of 7 and y-intercept of -6

Answers
Jackrabbits are capable of reaching speeds up to 40 miles per hour. How fast is this in feet per second? (Round to the nearest whole number.)
Answers
Nick's mark on a test was 39.
This mark was 60%.
What was the total possible mark?
Answers
Answer:
65
Step-by-step explanation:
Since 39 is 60%, 100/60= 1 2/3
39*1 2/3 is 65
Find the common ratio of the geometric sequence 8, 16, 32, ...

Answers
Answer:
64?
Step-by-step explanation:
The system of equations is graphed on the coordinate plane.
y=-5/3x+3
y=1/3x - 3
Enter the coordinates of the solution to the system of equations
in the boxes.

Answers
Answer: The solution is (3, -2)
This means that x = 3 and y = -2 pair up together.
=====================================================
Explanation:
The solution is where the two lines cross. Note if we started at the origin (0,0) and moved to the right 3 units, and then down 2 units, we would arrive at the location (3, -2).
-----------------
As a way to check, we can plug x = 3 into each equation. We should get y = -2 as a result for each equation
y = (-5/3)x + 3
y = (-5/3)*3 + 3
y = -5+3
y = -2
The first equation is confirmed. Let's check the second equation
y = (1/3)x - 3
y = (1/3)*3 - 3
y = 1 - 3
y = -2
Both equations have the y value equal -2 when x = 3. Therefore, the overall solution is confirmed.
Colleen already owns 28 hair bands, and additional hair bands are priced at 1 for a dollar.
With $15 to spend on new hair bands, how many total hair bands can Colleen own?
Please help

Answers
Answer:
After buying additional hair bands, Colleen can own a total of 43 hair bands.
Step-by-step explanation:
Solving this problem entails of finding out the total number of hair bands Colleen can own, based on the amount she already owns and how many more she purchases. Start by reading the problem carefully to break down the information provided.
We know that Colleen already owns twenty eight hair bands. This is important to remember to include. The problem also states that she has a total of fifteen dollars and each individual hair band is priced at one dollar.
Because the hair bands are only a dollar, Colleen can purchase an additional fifteen hair bands.
Setting up an equation will help us solve. Here is how we could set up the equation:
(amount of hair bands already owned = 28) + (number hair bands bought = 15) = (total number of hair bands owned = x)
28 + 15 = x
The equation is now in place. Solve by adding both terms. This is how you will reach the answer.
28 + 15 = x
43 = x
This means that Colleen will have 43 hair bands in total, after purchasing fifteen hair bands.
When coding the phrase "supravesical fissure of urinary bladder," the main term to reference in the index is ________ .a. urinaryb. bladderc. fissured. supravesical
Answers
The correct option of the given question is option (c) fissure.
When coding the phrase "supravesical fissure of urinary bladder," the main term to reference in the index is c. fissure.
To know more about Coding visit:
https://brainly.com/question/29775307
#SPJ11
The main term to reference in the index when coding the phrase "supravesical fissure of urinary bladder" is c. fissure.
In medical coding, the index is typically organized alphabetically based on the main terms or significant words within medical terminology. In this case, "fissure" is the main term that represents the specific condition or anatomical feature being coded.
The other terms, such as "urinary," "bladder," and "supravesical," provide additional context but are not the primary focus when searching for the appropriate code in the index.
To know more about Fissure related question visit:
https://brainly.com/question/28953403
#SPJ11
Your newspaper article will end with recommendations to fans about buying
tickets. Your research indicates the average local baseball fan plans to attend
67 games during the season. What are your recommendations to the average
fan about buying tickets? Should they buy season tickets or single-game
tickets?
Make a recommendation for fans buying tickets in each section:
• main box
• bleachers
• left field reserve
Include all necessary work to support your answer.
Answers
I recommend the average fan buy season tickets when purchasing seats.
Based on the research, the average local baseball fan plans to attend 67 games during the season. For a fan who is planning to attend this many games, it would be more cost-effective to purchase season tickets rather than individual game tickets.
For fans considering season tickets, here are some recommendations based on the seating section:
Main Box: If cost is not a concern and the fan is looking for a premium experience, purchasing season tickets in the Main Box section is the way to go. The fan will have the best view of the field and access to the best amenities.Bleachers: For the more budget-conscious fan who wants to attend the most games possible, purchasing season tickets in the Bleachers section is the best choice. These tickets are typically the least expensive and provide an energetic atmosphere with a close view of the field.Left Field Reserve: For fans who want a good balance between cost and comfort, season tickets in the Left Field Reserve section would be a good option. These tickets are often priced in between Main Box and Bleachers tickets and provide a good view of the field.Purchasing season tickets rather than individual game tickets is the most cost-effective choice for the average fan who plans to attend 67 games during the season. The best choice of section will depend on the fan's budget and personal preferences.
Learn more about ticket price here: brainly.com/question/11418438
#SPJ4
If f(x) = 6x - 4. what is f(x) when x = 8?
Answers
Answer:
44
Step-by-step explanation:
* means multiply
put 8 where the x is
6 * 8 - 4
48 - 4
44
which expression is equal to 6 (3x+4) ?
Answers
Answer: 18x+24
Step-by-step explanation:
find the surface area of a cylinder with a base diameter of 4 yd and a height of 4 yd . write your answer in terms of π , and be sure to include the correct unit. How do I solve this?
Answers
Answer:
Surface area of cylinder = 24π
Step-by-step explanation:
Given:
Base diameter = 4 yd
So Radius = 4 / 2 = 2 yd
Height = 4 yd
Find:
Surface area of cylinder
Computation:
Surface area of cylinder = 2πr(h+r)
Surface area of cylinder = 2π(2)(4+2)
Surface area of cylinder = 2π(2)(6)
Surface area of cylinder = 24π
screenshot underneath

Answers
Simplify them
Answer =11

a= bc-3c-3b/6c
look at the screenshots for steps



