Each square below represents one whole.
What percent is represented by the shaded area?

Answers
9514 1404 393
Answer:
110%
Step-by-step explanation:
Each stripe is 1/10 of a whole, so represents 100%/10 = 10% of the whole.
There are 11 shaded stripes, representing 11×10% = 110%.
Related Questions
solve the following question

Answers
14. The trigonometric equation (sin47°/cos43°)² + (cos43°/sin47°)² - 4cos²45° = 4
15. In the trigonometric equation 2(cos²θ - sin²θ) = 1, θ = 15°
What is a trigonometric equation?A trigonometric equation is an equation that contains a trigonometric ration.
14. To find the value of (sin47°/cos43°)² + (cos43°/sin47°)² - 4cos²45°, we proceed as follows
Since we have the trigonometric equation (sin47°/cos43°)² + (cos43°/sin47°)² - 4cos²45°,
We know that sin47° = sin(90 - 43°) = cos43°. So, substituting this into the equation, we have that
(sin47°/cos43°)² + (cos43°/sin47°)² - 4cos²45° = (cos43°/cos43°)² + (cos43°/cos43°)² - 4cos²45°
= 1² + 1² - 4cos²45°
We know that cos45° = 1/√2. So, we have
1² + 1² - 4cos²45° = 1² + 1² - 4(1/√2)²
= 1 + 1 + 4/2
= 2 + 2
= 4
So, (sin47°/cos43°)² + (cos43°/sin47°)² - 4cos²45° = 4
15. If 2(cos²θ - sin²θ) = 1 and θ is a positive acute angle, we need to find the value of θ. We proceed as follows
Since we have the trigonometric equation 2(cos²θ - sin²θ) = 1
We know that cos2θ = cos²θ - sin²θ. so, substituting this into the equation, we have that
2(cos²θ - sin²θ) = 1
2(cos2θ) = 1
cos2θ = 1/2
Taking inverse cosine, we have that
2θ = cos⁻¹(1/2)
2θ = 30°
θ = 30°/2
θ = 15°
So, θ = 15°
Learn more about trigonometric equation here:
https://brainly.com/question/28025415
#SPJ1
If a ring costs a jeweler $2100, at what price should it be sold to yield a profit of 50% on the selling price?
Answers
2100/2 = 1050
Meaning 50% is $1050
please help and answer ASAP please will mark Brainlest
What is the value of x?
Enter your answer in the box.
x =
°

Answers
Answer:
80 degrees
Step-by-step explanation:
The sum of the angles in a triangle is 180 degrees so we can create the equation 70+30+x=180. This solves out to 80 so x=80 degrees.
Adult tickets to a basketball game cost $5. Student tickets cost $1. A total of $3,142 was collected on the sale of 1,330 tickets. How many of each type of ticket were sold?
The basketball game sold
______adult tickets and
_______student tickets.
Answers
Answer:
453 adult tickets and 877 student tickets were sold.
Step-by-step explanation:
Given that adult tickets to a basketball game cost $ 5 and student tickets cost $ 1, and a total of $ 3,142 was collected on the sale of 1,330 tickets, to determine how many of each type of ticket were sold the following calculations must be performed:
5 - 1 = 4
1330 x 1 = 1330
3142 - 1330 = 1812
1812/4 = 453
1330 - 453 = 877
877 x 1 + 453 x 5 = X
877 + 2265 = X
3142 = X
Therefore, 453 adult tickets and 877 student tickets were sold.
need help............

Answers
Answer:
Answer=A
Step-by-step explanation:
(when dividing two powers we subtract the upper power by the bottom one)
\(\frac{7^{10} }{7^{3} }\)
=\(7^{10-3}\)
\(7^{7}\)
Complete the table of values for the equation 4x + 2y =64
Answers
The completed table of values for the equation 4x + 2y = 64 is provided .
To complete the table of values for the equation 4x + 2y = 64, we can assign different values to x and solve for y. Let's choose a range of values for x and calculate the corresponding values of y.
Table of Values:
x y
0 32
4 28
8 24
12 20
16 16
20 12
24 8
28 4
32 0
To find the values of y, we substitute each x-value into the equation and solve for y. For example, when x is 0, we have 4(0) + 2y = 64, which simplifies to 2y = 64 and y = 32. Similarly, for x = 4, we have \(4(4) + 2y = 64\), which simplifies to \(16 + 2y = 64\) and\(y = 28.\)
By continuing this process for the remaining values of x, we can complete the table of values for the equation 4\(x + 2y = 64.\)
For more questions on equation
https://brainly.com/question/29174899
#SPJ8
Please help!!!!!
(50 points)

Answers
Answer:Hope this helps
Step-by-step explanation:
Now classify the polynomial.
5x
A linear monomial
B quintic binomial
C. quadratic binomial
Answers
PLSS HELP MEEE ITS MATH ND IDRK HOW TO ANSWER ITT

Answers
Answer: D is the answer. trust me.
Step-by-step explanation:
The problem that could be solved using the equation 10x+5=35 is option D: After a $5 discount, an order of 10 items cost $35. How much did each item cost?
To solve this problem, we can use the equation 10x + 5 = 35, where x represents the cost of each item. The $5 discount reduces the total cost of the 10 items by $5, so the total cost of the 10 items before the discount would be 10x. Therefore, we can set up the equation:
10x + 5 = 35
Subtracting 5 from both sides, we get:
10x = 30
Dividing both sides by 10, we get:
x = 3
So, each item cost $3 before the discount.
Answer:
A
Step-by-step explanation:
Bridges in mathematics grade book page 124 answers
Answers
A statistician calculates that 8% of Americans own a Rolls Royce.
If the statistician is right, what is the probability that the proportion of Rolls Royce owners in a sample of 694 Americans would differ from the population proportion by less than 3%? Round your answer to four decimal places.
Answers
The probability that the proportion of Rolls Royce owners in a sample of 694 Americans would differ from the population proportion by less than 3% is; 0.36%
How to use the central limit theorem?
The Central Limit Theorem states that, for a normally distributed random variable X, with mean μ and standard deviation σ, the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean μ and standard deviation s = σ/√n
The standard deviation for proportion is given by the formula;
s = √(p(1 - p)/n)
We are given;
p = 8% = 0.08
n = 694
Thus;
s = √(0.08(1 - 0.08)/694)
s = 0.0103
Proportion above 8% + 3% = 11% or below 8% - 3% = 5%. Due to the fact that the normal distribution is symmetric, the probabilities will be equal, and as a result, we find one of them and multiply by 2.
Probability the proportion is less than 5%:
P-value of Z when X = 0.05.
z = (X - μ)/s
z = (0.05 - 0.08)/0.0103
z = -2.91
From p-value from z-score calculator, we have;
p-value = 0.001807
We multiply it by 2 to get the probability
Probability = 2 * 0.001807 = 0.0036 = 0.36%
Read more about central limit theorem at; https://brainly.com/question/25800303
#SPJ1
PLS! Due in 30 Minutes :( Help me with this graphing question. High school level

Answers
The set of points related to an exponential function and matched with set of translated points are, respectively:
(x, y) = (- 1, 0.5) → (x', y') = (2, - 1.5)
(x, y) = (0, 1) → (x', y') = (3, - 1)
(x, y) = (2, 4) → (x', y') = (5, 2)
(x, y) = (3, 8) → (x', y') = (6, 6)
(x, y) = (1, 2) → (x', y') = (4, 0)
(x, y) = (- 2, 0.25) → (x', y') = (1, - 1.75)
How to match a set of points related to an exponential function with a set of translated points
According to statemente, we find the case of set of points related to an exponential function and a set of translated points, after a quick inspection we derive the transformation rule:
Horizontal translation: 3 units right, vertical translation: 2 units down.
Now we check the statement on each ordered pair:
(x, y) = (- 1, 0.5):
(x', y') = (- 1, 0.5) + (3, - 2) = (2, - 1.5)
(x, y) = (0, 1):
(x', y') = (0, 1) + (3, - 2) = (3, - 1)
(x, y) = (2, 4):
(x', y') = (2, 4) + (3, - 2) = (5, 2)
(x, y) = (3, 8):
(x', y') = (3, 8) + (3, - 2) = (6, 6)
(x, y) = (1, 2):
(x', y') = (1, 2) + (3, - 2) = (4, 0)
(x, y) = (- 2, 0.25):
(x', y') = (- 2, 0.25) + (3, - 2) = (1, - 1.75)
To learn more on translations: https://brainly.com/question/29712965
#SPJ1
Through calculations, Jack and Kelsey estimated the diameter of the fountain in the park. If the actual length is 15 feet, which student's estimate is more accurate? Explain your reasoning.
Answers
Answer:
cual es? ósea la pregunta?
HELP (20 points) using triangle ABC how does extending vertex c further away to the left of vertex b verify the relationship between sides and angles in triangles?

Answers
Answer:
a stays the same but cb cahanges
Step-by-step explanation:
This is the bone density score separating the bottom, 7% from the top 93%
Answers
This means that bone density scores below -1.88 are in the bottom 7% of scores, and scores above 1.88 are in the top 93% of scores.
What is Algebraic expression ?
Algebraic expression can be defined as combination of variables and constants.
It is relates to bone density score distribution, where the bottom 7% of scores are separated from the top 93% of scores. This could be interpreted in a few different ways, but here's one way to approach it:
If we assume that the bone density scores are normally distributed (which is a common assumption in statistics), then we can use the properties of the normal distribution to estimate the cutoff values for the bottom 7% and top 93% of scores.
The standard normal distribution has a mean of 0 and a standard deviation of 1. Using this distribution, we can look up the cutoff values for the bottom 7% and top 93% of scores using a standard normal distribution table or calculator. These cutoff values represent the bone density scores below which 7% of scores fall and above which 93% of scores fall.
For example, using a standard normal distribution table, we can find that the cutoff value for the bottom 7% of scores is approximately -1.88, and the cutoff value for the top 93% of scores is approximately 1.88.
Therefore, This means that bone density scores below -1.88 are in the bottom 7% of scores, and scores above 1.88 are in the top 93% of scores.
To learn more about Algebraic expression from given link.
brainly.com/question/953809
#SPJ1
Which number line shows the solution if 4x - 36 < -12?
Answers
One solution was found :
x = 9
-3 < n < 1
n is an integer.
Write down the possible values of n.
Answers
Answer:
-2, -1
Step-by-step explanation:
they're the only integers you can get
For an investment of 26,245, a quarterly statement reports that the account is 26,292. The statement reports that for the same quarter, the rate of return of the investment was - 0.02%. Given the information regarding the investment quarterly activity, does the reported rate of return seem reasonable?
Answers
No. The reported return rate appears lower than expected.
Rate of returnsTo determine whether the reported rate of return is reasonable or not, we can calculate the expected rate of return based on the investment amount and the ending value of the account.
First, we need to calculate the total number of quarters that have elapsed between the initial investment and the current quarter. Let's assume that the investment has been held for n quarters.
Then, we can use the following formula to calculate the expected rate of return:
Expected rate of return = (Ending value / Initial investment) ^ (1/n) - 1
Plugging in the given values, we get:
n = 1 (since we are only given information for a single quarter)
Initial investment = 26,245
Ending value = 26,292
Expected rate of return = (26,292 / 26,245) ^ (1/1) - 1 = 0.18%
Comparing the expected rate of return of 0.18% with the reported rate of return of -0.02%, we can see that they are quite different. However, it's important to note that a single quarter's rate of return may not be indicative of the overall performance of the investment.
Therefore, while the reported rate of return seems lower than expected, we would need to consider the performance over a longer period of time to make a more informed assessment of the investment's performance.
More on rate of returns can be found here: https://brainly.com/question/24232401
#SPJ1
if john is 13 what will he be in 63 years
Answers
Answer:
76
Step-by-step explanation:
Answer: 76
Step-by-step explanation: may be dead
I need help please tell the right answer

Answers
Answer: 47.6 is your answer hope this helped
plz make brainly
Step-by-step explanation:
Answer:
36 - 4
Step-by-step explanation:
(6x - 2)(6x + 2)
= (6x)(6x) + (6x)(-2) + (2)(6x) + (-2)(2)
= 36 - 12x + 12x - 4
= 36 - 4Step-by-step explanation:
Approximate the logarithm using the properties of logarithms, given
logb 2 ≈ 0.3562,
logb 3 ≈ 0.5646,
and
logb 5 ≈ 0.8271.
(Round your answer to four decimal places.)
㏒b(2b^3)
Answers
que representa Laos hombres con relacion al total
What is 35 degree angle in standard position?

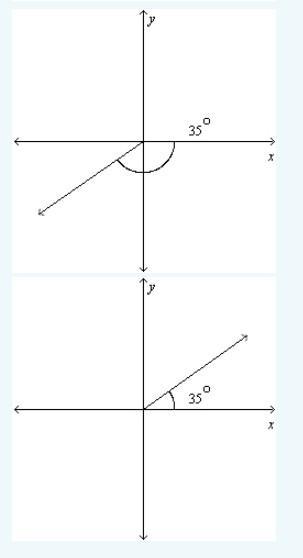
Answers
After using ruler and following the steps described below
We get the standard position of 35 degree.
The given angle is = 35 degree
To draw standard position of angle:
We proceed it to draw by ruler
So, in order to get position,
Follow the following steps:
1: Draw a straight line with your ruler.
2: Place your protractor on the line and align the base of the protractor with the line.
3: Find the 35 degree mark on the protractor and make a small mark on the line at that point.
4: Move your protractor to the mark you just made.
5: Align the base of the protractor with the line and make another small mark on the line at the 35 degree mark.
6: Draw a straight line connecting the two points you just marked.
And there you have it! A 35 degree angle drawn on paper.
And after following these steps we get the standard potion angle 35 degree.
Learn more about the angle visit:;
https://brainly.com/question/25716982d
#SPJ1

Which of the following describes a situation for finding volume?
A) The amount of cereal inside a cereal box
B) The amount of space a garden takes up in the backyard
C) The total square feet of a kitchen floor
D) The amount of floor space that a rug covers
Answers
Answer:
A) The amount of cereal inside a cereal box.
Hope this helps
To solve the problem we must know about the volume.
What is Volume?Volume is described as the total amount of space taken by an object. It is a scalar quantity and it is 3 dimensional.
The amount of cereal inside a cereal box has volume.
As we know that the cereal box has space inside to hold something therefore, the cereals or something can be put inside this that will make the space inside the box. Also, the box has length, breadth, and height, therefore, it is 3 dimensional.
Hence, the amount of cereal inside a cereal box has volume.
Learn more about Volume:
https://brainly.com/question/1578538
Find the measure of Arc AD.
Pls help me

Answers
Answer:
arc AD = 138°
Step-by-step explanation:
Recall: if two inscribed angles are subtended by the same arc, the two angles are congruent or equal to each other based on the inscribed angle theorem.
<ABD and <ACD are two inscribed angles subtended by the same arc, therefore, they are equal.
Thus:
7x + 20 = 55 + 2x
Solve for x. Collect like terms
7x - 2x = 55 - 20
5x = 35
Divide both sides by 5
x = 35/5
x = 7
✔️m<ACD = ½(arc AD) (Inscribed angle theorems)
Substitute
55 + 2x = ½(arc AD)
Plug in the value of x
55 + 2(7) = ½(arc AD)
55 + 14 = ½(Arc AD)
69 = ½(Arc AD)
Multiply both sides by 2
2*69 = Arc AD
138° = arc AD
arc AD = 138°
Which statement is true about the graphed function

Answers
A homeowner wants to carpet three rooms that measure 12 ft 12 ft, 10 ft x 14 ft, and 21 ft x 20 ft. How many square yards of carpet should be ordered, rounded to the nearest tenth?
Answers
1000 tickets were sold . Adult tickets cost 8.50 , children’s cost 4.50 and total of 7300 was collected. How many tickets of each kind were sold ?
Answers
tanx(1+cos2x)=sin2x prove the identity
Answers
Using double angle identity, we are able to prove tan(x)(1 + cos(2x)) = sin(2x).
What is the prove of the given identity?To prove the identity tan(x)(1 + cos(2x)) = sin(2x), we can start by using trigonometric identities to simplify both sides of the equation.
Starting with the left-hand side (LHS):
tan(x)(1 + cos(2x))
We know that tan(x) = sin(x) / cos(x) and that cos(2x) = cos²(x) - sin²(x). Substituting these values, we get:
LHS = (sin(x) / cos(x))(1 + cos²(x) - sin²(x))
Next, we can simplify the expression by expanding and combining like terms:
LHS = sin(x) / cos(x) + sin(x)cos²(x) / cos(x) - sin³(x) / cos(x)
Simplifying further:
LHS = sin(x) / cos(x) + sin(x)cos(x) - sin³(x) / cos(x)
Now, let's work on the right-hand side (RHS):
sin(2x)
Using the double angle identity for sine, sin(2x) = 2sin(x)cos(x).
Now, let's compare the LHS and RHS expressions:
LHS = sin(x) / cos(x) + sin(x)cos(x) - sin³(x) / cos(x)
RHS = 2sin(x)cos(x)
To prove the identity, we need to show that the LHS expression is equal to the RHS expression. We can combine the terms on the LHS to get a common denominator:
LHS = [sin(x) - sin³(x) + sin(x)cos²(x)] / cos(x)
Now, using the identity sin²(x) = 1 - cos²(x), we can rewrite the numerator:
LHS = [sin(x) - sin³(x) + sin(x)(1 - sin²(x))] / cos(x)
= [sin(x) - sin³(x) + sin(x) - sin³(x)] / cos(x)
= 2sin(x) - 2sin³(x) / cos(x)
Now, using the identity 2sin(x) = sin(2x), we can simplify further:
LHS = sin(2x) - 2sin³(x) / cos(x)
Comparing this with the RHS expression, we see that LHS = RHS, proving the identity.
Learn more on trigonometric identity here;
https://brainly.com/question/24496175
#SPJ1
Heeeelp please, Can be zero or not?
with all steps and explanay.

Answers
The value of integral is 3.
Let's evaluate the integral over the positive half of the interval:
∫[0 to π] (cos(x) / √(4 + 3sin(x))) dx
Let u = 4 + 3sin(x), then du = 3cos(x) dx.
Substituting these expressions into the integral, we have:
∫[0 to π] (cos(x) / sqrt(4 + 3sin(x))) dx = ∫[0 to π] (1 / (3√u)) du
Using the power rule of integration, the integral becomes:
∫[0 to π] (1 / (3√u)) du = (2/3) . 2√u ∣[0 to π]
Evaluating the definite integral at the limits of integration:
(2/3)2√u ∣[0 to π] = (2/3) 2(√(4 + 3sin(π)) - √(4 + 3sin(0)))
(2/3) x 2(√(4) - √(4)) = (2/3) x 2(2 - 2) = (2/3) x 2(0) = 0
So, the value of integral is
= 3-0
= 3
Learn more about Definite integral here:
https://brainly.com/question/30760284
#SPJ1
Answer:
\(3-\displaystyle \int^{\pi}_{-\pi} \dfrac{\cos x}{\sqrt{4+3 \sin x}}\; \text{d}x\approx 0.806\; \sf (3\;d.p.)\)
Step-by-step explanation:
First, compute the indefinite integral:
\(\displaystyle \int \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x\)
To evaluate the indefinite integral, use the method of substitution.
\(\textsf{Let} \;\;u = 4 + 3 \sin x\)
Find du/dx and rewrite it so that dx is on its own:
\(\dfrac{\text{d}u}{\text{d}x}=3 \cos x \implies \text{d}x=\dfrac{1}{3 \cos x}\; \text{d}u\)
Rewrite the original integral in terms of u and du, and evaluate:
\(\begin{aligned}\displaystyle \int \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&=\int \dfrac{\cos x}{\sqrt{u}}\cdot \dfrac{1}{3 \cos x}\; \text{d}u\\\\&=\int \dfrac{1}{3\sqrt{u}}\; \text{d}u\\\\&=\int\dfrac{1}{3}u^{-\frac{1}{2}}\; \text{d}u\\\\&=\dfrac{1}{-\frac{1}{2}+1} \cdot \dfrac{1}{3}u^{-\frac{1}{2}+1}+C\\\\&=\dfrac{2}{3}\sqrt{u}+C\end{aligned}\)
Substitute back u = 4 + 3 sin x:
\(= \dfrac{2}{3}\sqrt{4+3\sin x}+C\)
Therefore:
\(\displaystyle \int \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x= \dfrac{2}{3}\sqrt{4+3\sin x}+C\)
To evaluate the definite integral, we must first determine any intervals within the given interval -π ≤ x ≤ π where the curve lies below the x-axis. This is because when we integrate a function that lies below the x-axis, it will give a negative area value.
Find the x-intercepts by setting the function to zero and solving for x in the given interval -π ≤ x ≤ π.
\(\begin{aligned}\dfrac{\cos x}{\sqrt{4+3\sin x}}&=0\\\\\cos x&=0\\\\x&=\arccos0\\\\\implies x&=-\dfrac{\pi }{2}, \dfrac{\pi }{2}\end{aligned}\)
Therefore, the curve of the function is:
Below the x-axis between -π and -π/2.Above the x-axis between -π/2 and π/2.Below the x-axis between π/2 and π.So to calculate the total area, we need to calculate the positive and negative areas separately and then add them together, remembering that if you integrate a function to find an area that lies below the x-axis, it will give a negative value.
Integrate the function between -π and -π/2.
As the area is below the x-axis, we need to negate the integral so that the resulting area is positive:
\(\begin{aligned}A_1=-\displaystyle \int^{-\frac{\pi}{2}}_{-\pi} \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&=- \left[\dfrac{2}{3}\sqrt{4+3\sin x}\right]^{-\frac{\pi}{2}}_{-\pi}\\\\&=-\dfrac{2}{3}\sqrt{4+3 \sin \left(-\frac{\pi}{2}\right)}+\dfrac{2}{3}\sqrt{4+3 \sin \left(-\pi\right)}\\\\&=-\dfrac{2}{3}\sqrt{4+3 (-1)}+\dfrac{2}{3}\sqrt{4+3 (0)}\\\\&=-\dfrac{2}{3}+\dfrac{4}{3}\\\\&=\dfrac{2}{3}\end{aligned}\)
Integrate the function between -π/2 and π/2:
\(\begin{aligned}A_2=\displaystyle \int^{\frac{\pi}{2}}_{-\frac{\pi}{2}} \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&= \left[\dfrac{2}{3}\sqrt{4+3\sin x}\right]^{\frac{\pi}{2}}_{-\frac{\pi}{2}}\\\\&=\dfrac{2}{3}\sqrt{4+3 \sin \left(\frac{\pi}{2}\right)}-\dfrac{2}{3}\sqrt{4+3 \sin \left(-\frac{\pi}{2}\right)}\\\\&=\dfrac{2}{3}\sqrt{4+3 (1)}-\dfrac{2}{3}\sqrt{4+3 (-1)}\\\\&=\dfrac{2\sqrt{7}}{3}-\dfrac{2}{3}\\\\&=\dfrac{2\sqrt{7}-2}{3}\end{aligned}\)
Integrate the function between π/2 and π.
As the area is below the x-axis, we need to negate the integral so that the resulting area is positive:
\(\begin{aligned}A_3=-\displaystyle \int^{\pi}_{\frac{\pi}{2}} \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&= -\left[\dfrac{2}{3}\sqrt{4+3\sin x}\right]^{\pi}_{\frac{\pi}{2}}\\\\&=-\dfrac{2}{3}\sqrt{4+3 \sin \left(\pi\right)}+\dfrac{2}{3}\sqrt{4+3 \sin \left(\frac{\pi}{2}\right)}\\\\&=-\dfrac{2}{3}\sqrt{4+3 (0)}+\dfrac{2}{3}\sqrt{4+3 (1)}\\\\&=-\dfrac{4}{3}+\dfrac{2\sqrt{7}}{3}\\\\&=\dfrac{2\sqrt{7}-4}{3}\end{aligned}\)
To evaluate the definite integral, sum A₁, A₂ and A₃:
\(\begin{aligned}\displaystyle \int^{\pi}_{-\pi} \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&=\dfrac{2}{3}+\dfrac{2\sqrt{7}-2}{3}+\dfrac{2\sqrt{7}-4}{3}\\\\&=\dfrac{2+2\sqrt{7}-2+2\sqrt{7}-4}{3}\\\\&=\dfrac{4\sqrt{7}-4}{3}\\\\ &\approx2.194\; \sf (3\;d.p.)\end{aligned}\)
Now we have evaluated the definite integral, we can subtract it from 3 to evaluate the given expression:
\(\begin{aligned}3-\displaystyle \int^{\pi}_{-\pi} \dfrac{\cos x}{\sqrt{4+3 \sin x}}\; \text{d}x&=3-\dfrac{4\sqrt{7}-4}{3}\\\\&=\dfrac{9}{3}-\dfrac{4\sqrt{7}-4}{3}\\\\&=\dfrac{9-(4\sqrt{7}-4)}{3}\\\\&=\dfrac{13-4\sqrt{7}}{3}\\\\&\approx 0.806\; \sf (3\;d.p.)\end{aligned}\)
Therefore, the given expression cannot be zero.

Based on the graph, if Joe earned $400, how many hours did he work?
