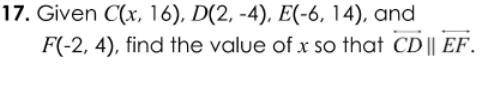Answers
Answer:
x = - 6
Step-by-step explanation:
Parallel lines have equal slopes
Calculate the slopes of EF and CD and equate them
Calculate slopes using the slope formula
m = \(\frac{y_{2}-y_{1} }{x_{2}-x_{1} } \)
with (x₁, y₁ ) = E (- 6, 14 ) and F (- 2, 4 )
\(m_{EF} \) = \(\frac{4-14}{-2-(-6)} \) = \(\frac{-10}{-2+6} \) = \(\frac{-10}{4} \) = - \(\frac{5}{2} \)
Repeat with (x₁, y₁ ) = C (x, 16 ) and (x₂, y₂ ) = D (2, - 4 )
\(m_{CD} \) = \(\frac{-4-16}{2-x} \) = \(\frac{-20}{2-x} \)
Equate the 2 slopes and solve for x
\(\frac{-20}{2-x} \) = \(\frac{5}{-2} \) ( cross- multiply )
5(2 - x) = 40 ( divide both sides by 5 )
2 - x = 8 ( subtract 2 from both sides )
- x = 6 ( multiply both sides by - 1 )
x = - 6
Related Questions
In an effort to persuade customers to reduce their electricity consumption, special discounts have been offered for low consumption customers. In Florida, the EPA estimates that 70% of the residences have qualified for these discounts. If, instead, a sample of 20 residences is selected, what is the probability 12 or more will have qualified for the discounts
Answers
Answer:
please mark me brainlist
Step-by-step explanation:
p = proportion of residents qualified for discounts = 0.70
Sample size = 20
If X is the no of residences selected for discounts then x is binomial with (20,0.7)
P(X>=12) = 0.8867
Hello I need help. What's 10.40 + 66.9 + 100.4 x 2 =
help please
Answers
Answer:
278.1
Step-by-step explanation:
Follow order of operations
Multipacation first (in this situation) and then just add left to right :)
a rectangular water tank has length 25 ft, width 10 ft, and depth 15 ft. if the tank is full, how much work does it take to pump all the water out? (water weights
Answers
It takes 3,510,000 ft-lbs of work to pump all the water out of the rectangular water tank.
To calculate the work done in pumping all the water out of a rectangular water tank, we need to find the volume of the tank and then multiply it by the weight of water and the distance it needs to be lifted.
Step 1: Calculate the volume of the tank.
The volume of a rectangular tank can be calculated using the formula:
Volume = length × width × depth
In this case:
length = 25 ft
width = 10 ft
depth = 15 ft
Volume = 25 ft × 10 ft × 15 ft = 3750 cubic feet
Step 2: Find the weight of the water in the tank.
The weight of water is given as 62.4 pounds per cubic foot.
Therefore, the weight of the water in the tank is:
Weight = Volume × Weight per cubic foot
Weight = 3750 cubic ft × 62.4 lbs/cubic ft = 234000 lbs
Step 3: Calculate the work done.
Since the depth of the tank is 15 ft, we can assume that the water needs to be pumped out to a height of 15 ft.
Work can be calculated using the formula:
Work = Force × Distance
In this case:
Force = Weight of the water = 234000 lbs
Distance = Depth of the tank = 15 ft
Work = 234000 lbs × 15 ft = 3,510,000 ft-lbs.
For similar question on rectangular.
https://brainly.com/question/29466399
#SPJ11
View image trig maths

Answers
The value cosθ is 0.707.
The value angle z is -45⁰, and 45⁰.
The value of angle θ is 45⁰ and 315⁰.
What is the cosθ?The value cosθ, and angle Z is calculated by applying trigonometry ratio as follows;
for question 6,
tan θ = opposite side/adjacent
tan θ = 5/5
tan θ = 1
θ = 45⁰ = z
cos θ = 0.707
for question 7;
tan z = opp/adjacent
tan z = -5/5
tan z = -1
z = arc tan (-1)
z = -45⁰ =
The value of θ is calculated as;
θ = 360 - 45
θ = 315
cos (315) = 0.707
Learn more about trig ratios here: https://brainly.com/question/10417664
#SPJ1
If the 4th and 7th terms of a geometric sequence are 1/16 and
1/128, then the sum of the first 7 terms of this sequence is equal
to
Answers
Therefore, the sum of the first 7 terms of the given geometric sequence is 127/128.
To find the sum of the first 7 terms of a geometric sequence, we need to determine the common ratio and the first term of the sequence.
Let's denote the first term of the sequence as 'a' and the common ratio as 'r'.
Given that the 4th term is 1/16 and the 7th term is 1/128, we can write the following equations:
a * r^3 = 1/16 (equation 1)
a * r^6 = 1/128 (equation 2)
Dividing equation 2 by equation 1, we get:
(r^6)/(r^3) = (1/128)/(1/16)
r^3 = 1/8
Taking the cube root of both sides, we find:
r = 1/2
Substituting the value of r back into equation 1, we can solve for 'a':
a * (1/2)^3 = 1/16
a * 1/8 = 1/16
a = 1/2
Now we have the first term 'a' as 1/2 and the common ratio 'r' as 1/2.
The sum of the first 7 terms of the geometric sequence can be calculated using the formula:
Sum = a * (1 - r^n) / (1 - r)
Substituting the values into the formula, we have:
Sum = (1/2) * (1 - (1/2)^7) / (1 - 1/2)
Simplifying the expression
Sum = (1/2) * (1 - 1/128) / (1/2)
Sum = (1/2) * (127/128) / (1/2)
Sum = (127/128)
For such more question on ratio
https://brainly.com/question/2914376
#SPJ8
santiago needs to build a ramp 3 times longer in every dimension than the ramp he has, which is in the shape of a triangular prism with surface area 40.2 ft2 . what is the surface area of the new ramp, in square feet? do not round your answer.
Answers
To solve this problem, we need to use the formula for surface area of a triangular prism, which is: Surface Area = 2 × (base area) + (lateral area). So, the surface area of the new ramp that Santiago needs to build is 361.8 square feet.
Let's first find the base area of Santiago's current ramp. Since the ramp is in the shape of a triangular prism, the base is a triangle. Let's call the base dimensions b and h, and the length of the ramp l. Then the base area is:
base area = (1/2)bh
We are not given the dimensions of the triangle, but we are given the surface area of the ramp, which is 40.2 ft^2. So we can set up an equation:
2 × (base area) + (lateral area) = 40.2
Substituting the formula for base area, we get:
2 × (1/2)bh + (lateral area) = 40.2
Simplifying:
bh + (lateral area) = 40.2
Now we need to find the lateral area. Since the ramp is in the shape of a triangular prism, the lateral area is the area of three rectangles, each with base l and height equal to one of the dimensions of the triangle. Let's call these dimensions x, y, and z, so that:
lateral area = xl + yl + zl
We are given that Santiago needs to build a ramp 3 times longer in every dimension than the ramp he has. So the new dimensions of the triangle are 3b, 3h, and 3l. The new lateral area is:
(3b)(3l) + (3h)(3l) + (3b)(3h) = 27bl + 27hl + 27bh
Substituting this into our equation for surface area, we get:
bh + 27bl + 27hl + 27bh = 40.2
Simplifying:
55bh + 27bl + 27hl = 40.2
Now we can solve for the new surface area by using the formula for surface area again, but with the new dimensions:
Surface Area = 2 × (base area) + (lateral area)
Substituting in the new dimensions, we get:
Surface Area = 2 × (1/2)(3b)(3h) + (27bl + 27hl + 27bh)
Simplifying:
Surface Area = 9bh + 54bl + 54hl
Substituting in the equation we found earlier:
Surface Area = 9bh + 54bl + 54hl = (40.2 - 27bl - 27hl)/55
Multiplying both sides by 55:
495bh + 2970bl + 2970hl = 40.2 - 27bl - 27hl
Simplifying:
522bh + 2997bl + 2997hl = 40.2
So the surface area of the new ramp is 522bh + 2997bl + 2997hl square feet.
learn more about triangular prism here: brainly.com/question/24046619
#SPJ11
Brainliest will be rewarded+ 100 points!!
Take a screen shot of the work and do the work on the ss

Answers
Answer: When do you need it done?
Step-by-step explanation: ?
Answer:
Step-by-step explanation:
x+y=17
x-y = 7
From equation 2, x = 7 + y
put this in equation 1.
(7+y) + y = 17
7+2y = 17
2y = 10
y = 5.
We said that x = 7+y
thus, x = 7 + 5
x = 12.
2x+2y=36
2(x+y) = 36
Thus, x + y = 18.
x+y = 18
x-y=6 using elimination (literally simplifying this)
2x = 24 (y-y=0. ELIMINATED!)
x = 12
When x = 12,
x+y=18
12+y=18
y=6.
3x = y
x + y = 20
From 1, y = 3x.
x + (3x) = 20
4x = 20
x = 5.
when x = 5,
y = 3x
y = 3(5)
y = 15.
x+y = -4
xy = -21
from 1, x = -4-y
=> y(-4-y)= -21
-y²-4y = -21
Therefore,
y² + 4y -21 = 0
y= 3 or -7.
When y = 3,
x + 3 = -4
x= -7.
When y = -7,
x + (-7) = -4
x-7=-4
x = 3.
Hope these help! :)
*fingers cracking*
an investment project offers $4,350 per year forever, with the first payment occurring one year from now. if the interest rate is 6%, what would you pay to participate in this project?
Answers
The present value of this investment project is $72,500. This can be solved by the concept of Compound interest.
The perpetual cash flow of $4,350 per year can be considered as an annuity perpetuity, where the cash flow is constant forever. To calculate the present value of this perpetuity, we can use the formula:
Present Value = Annual Cash Flow / Discount Rate
Here, the annual cash flow is $4,350, and the discount rate is the interest rate of 6%. Thus, we can calculate the present value as:
Present Value = $4,350 / 0.06
Present Value = $72,500
Therefore, to participate in this investment project, you would need to pay $72,500 today to receive $4,350 per year forever, starting from one year from now
To learn more about Compound interest here:
brainly.com/question/14295570#
#SPJ11
If p is the hypothesis of a conditional statement and q is the conclusion, which is represented by q→p?
O the original conditional statement
O the inverse of the original conditional statement
O the converse of the original conditional statement
O the contrapositive of the original conditional statement
Answers
Answer:
(c) the converse of the original conditional statement
Step-by-step explanation:
If a conditional statement is described by p→q, you want to know what is represented by q→p.
Conditional variationsFor the conditional p→q, the variations are ...
converse: q→pinverse: p'→q'contrapositive: q'→p'As you can see from this list, ...
the converse of the original conditional statement is represented by q→p, matching choice C.
__
Additional comment
If the conditional statement is true, the contrapositive is always true. The inverse and converse may or may not be true.
<95141404393>
Can someone help me with this one

Answers
Answer:
#9 has 8 vertices
# 10 has 5 vertices
Step-by-step explanation:
A vertex is is a point where two or more curves, lines, or edges meet. The word "vertices" is the plural of the word "vertex."
If you solve the equation 6x + 2y = -14 for y, what would you get? *
Answers
Move 6x to the right side
2y = -6x - 14
Divide all numbers by 2 to isolate the variable
2y/2 = -6x/2 - 14/2
y = -3x - 7
I’m so confused about this problem:
1 5/9 ÷ -1/2
Can anyone help me?
(ToT)
Answers
Answer: -3.11111112
Step-by-step explanation:
1 and 5/9 as a decimal is 1.555555556
-1/2 as a decimal is -0.5
1.555555556 divided by -0.5 is -3.11111112
Three of these fractions are equivalent. Which one is the odd one out?

Answers
===========================================================
Explanation:
Using a calculator,
30/70 = 0.42857 approximately12/30 = 0.49/21 = 0.42857 approximately6/14 = 0.42857 approximatelyWe see that 12/30 = 0.4 is the odd one out.
The Equivalent Fraction are:
30/70, 9/21 and 6/14.
What is Fraction?The fractional bar is a horizontal bar that divides the numerator and denominator of every fraction into these two halves.
The number of parts into which the whole has been divided is shown by the denominator. It is positioned in the fraction's lower portion, below the fractional bar.How many sections of the fraction are displayed or chosen is shown in the numerator. It is positioned above the fractional bar in the upper portion of the fraction.To find the equivalent fraction we need to simplify the fraction.
First. 30/70
= 3/7
second, 12/30
= 6/15
= 3/5
third, 9/21
= 3 / 7
fourth, 6/14
= 3 /7
Learn more about Equivalent Fraction here:
https://brainly.com/question/29766013
#SPJ2
Find the value of x
A) 6
B) 22.2
C) 8
D) 80
5x
2x + 24
5.(2x124)
10x+120

Answers
Answer:
C) 8
Step-by-step explanation:
5x=2x+24
5x-2x=24
3x=24
x=8
A square is attached to a semicircle to make the figure shown in the diagram below .
if the radius of the semicircle is 4 meters ,what is the aproximate area of the figure .

Answers
Answer:
C) 89.12 m^2
Step-by-step explanation:
You can find the area of this figure by finding the areas of both shapes (semicircle and rectangle) then adding both areas.
To find the area of a semicircle, use this formula:
1/2πr^2 (1/2 x 3.14 x radius x radius)
Here, this radius is 4.
Now, we just plug in the numbers.
[3.14 is always used for π (pi)].
1/2 x 3.14 x radius x radius
↓
1/2 x 3.14 x 4 x 4 = 25.12
25.12 is the area of the semicircle.
Now, we must find the area of the square.
SQUARES ARE HAVE EQUAL SIDES, SO TO FIND THE AREA, WE SIMPLY MULTIPLY A SIDE LENGTH BY ITSELF TWICE.
8 x 8 = 64.
Now that we have both areas, we add to find the area of the figure.
25.12 + 64 = 89.12
Therefore, the area of this figure is 89.12 meters^2.
(2/3+5/2-7/3)+(3/2+7/3-5/6)
Answers
Answer:
after simplifying, we get,
23/6
Step-by-step explanation:
(2/3+5/2-7/3)+(3/2+7/3-5/6)
We simplify,
\((2/3+5/2-7/3)+(3/2+7/3-5/6)\\(2/3-7/3+5/2)+(3/2+7/3-5/6)\\(5/2-5/3)+(9/6+14/6-5/6)\\(15/6-10/6)+((9+14-5)/6)\\(15-10)/6+(23-5)/6\\5/6+18/6\\(5+18)/6\\23/6\)
1. a medical insurance company is analyzing the promptness of its claims department in responding to customer claims. the company has a policy of processing all claims received within five days. in order to determine how well the organization is doing, data were gathered to determine the proportion of time the claims were mailed late. a total of 24 sets of 100 samples each were made from which the proportion of claims that were mailed within the five-day limit was determined. (carry on three decimal points) sample number 1 2 3 4 5 6 7 8 9 10 11 12 number late 12 14 18 10 8 12 13 17 13 12 15 21 sample number 13 14 15 16 17 18 19 20 21 22 23 24 number late 19 17 23 24 21 9 20 16 11 8 20 7 do the data indicate a process is in control? why or why not?
Answers
To determine whether the process is in control or not, we can use a control chart. The control chart is a graphical tool used to monitor the stability of a process over time by plotting the sample statistics such as means or proportions over time and comparing them to control limits.
In this case, we are interested in monitoring the proportion of claims that were mailed within the five-day limit. We will use a p-chart, which is a control chart used to monitor the proportion of nonconforming items in a sample.
The formula for the p-chart is:
p = (number of nonconforming items in the sample) / (sample size)
The control limits for the p-chart are:
Upper control limit (UCL) = p-bar + 3sqrt(p-bar(1-p-bar)/n)
Lower control limit (LCL) = p-bar - 3sqrt(p-bar(1-p-bar)/n)
where p-bar is the overall proportion of nonconforming items, n is the sample size, and sqrt is the square root function.
Let's calculate the p-chart for the given data. The total number of samples is 24 and the sample size is 100.
First, we calculate the proportion of claims that were mailed within the five-day limit for each sample:
p1 = 1 - 12/100 = 0.88
p2 = 1 - 14/100 = 0.86
p3 = 1 - 18/100 = 0.82
p4 = 1 - 10/100 = 0.90
p5 = 1 - 8/100 = 0.92
p6 = 1 - 12/100 = 0.88
p7 = 1 - 13/100 = 0.87
p8 = 1 - 17/100 = 0.83
p9 = 1 - 13/100 = 0.87
p10 = 1 - 12/100 = 0.88
p11 = 1 - 15/100 = 0.85
p12 = 1 - 21/100 = 0.79
p13 = 1 - 19/100 = 0.81
p14 = 1 - 17/100 = 0.83
p15 = 1 - 23/100 = 0.77
p16 = 1 - 24/100 = 0.76
p17 = 1 - 21/100 = 0.79
p18 = 1 - 9/100 = 0.91
p19 = 1 - 20/100 = 0.80
p20 = 1 - 16/100 = 0.84
p21 = 1 - 11/100 = 0.89
p22 = 1 - 8/100 = 0.92
p23 = 1 - 20/100 = 0.80
p24 = 1 - 7/100 = 0.93
Next, we calculate the overall proportion of claims that were mailed within the five-day limit:
p-bar = (p1+p2+...+p24)/24 = 0.8575
Then, we calculate the control limits for the p-chart:
UCL = p-bar + 3sqrt(p-bar(1-p-bar)/n) = 0.8992
LCL = p-bar - 3sqrt(p-bar(1-p-bar)/n) = 0.8158
To learn more about the data visit:
brainly.com/question/13650923
#SPJ11
The siding of a house is 2250 square feet. The siding needs two coats of paint. One quart costs $18 and covers 80 square feet. One gallon costs $29 and covers 320 square feet. What is the minimum cost of the paint needed to complete the job? How much paint is left over?
Answers
Answer:
Minimum cost needed = $221
Remaining quart paint = 7/8
Step-by-step explanation:
Let
x = number of 1 gallon paints
y = number of 1 quart paints
1 gallon covers 320 square feet
1 quart covers 80 square feet
Number of gallons paint needed = Total siding of the house / 320 square feet
= 2250 / 320
= 7.0312
Approximately to the nearest whole number
Number of gallons paint needed = 7 gallons
Total siding of the house covered by gallons = 7 gallons × 320 square feet
= 2,240 square feet
Siding of the house remaining = Total siding - Siding covered
= 2,250 - 2,240
= 10 square feet
1 quart covers 80 feet
Therefore, 1 quart will cover the remaining 10 square feet
A. The minimum cost of the paint needed to complete the job
Total cost = (Price of gallons × Quantity of gallons needed) + (price of quart × Quantity of quart needed)
= (29 × 7) + (18 × 1)
= 203 + 18
= $221
Minimum cost needed = $221
B. How much paint is left over
Recall
1 quart covers 80 square feet
And remaining siding to be covered = 10 square feet
That is,
10/80 = 1/8 of a quart paint used
Remaining quart paint = 1 - 1/8
= 7/8 quart paint
Answer:
no
Step-by-step explanation:
no
Solve using the quadratic formula

Answers
The value of x in the equation is x = -1 and x = -4.67
How to solve using the quadratic formulaFrom the question, we have the following parameters that can be used in our computation:
3x^2 + 13x + 4 = 0
This is a quadratic equation that can be solved using the quadratic formula:
x = (-b ± √(b² - 4ac)) / 2a
where a = 3, b = 13, c = 4
So, we have
x = (-13 ± √(13² - 4 * 3 * 4)) / 2 * 3
x = (-17 ± √(169 +- 48)) /6
x = (-17 ± 11) /6
Expand
x = (-17 + 11)/6 and x = (-17 - 11)/6
Evaluate
x = -1 and x = -4.67
Read more about quadratic equation a
https://brainly.com/question/1214333
#SPJ1
HELP PLZ 12+points
Select the correct answer from the drop-down menu.
Luther and Nelson are seniors on the school basketball team. The box plots represent the number of points they scored in 20 randomly selected games.
The number of points Nelson scores in each game is generally__?___ the number of points Luther scores in each game.
CHOICES FOR THE BLANK:
A)greater than
B)less than
C)the same as

Answers
Answer:
more than
Step-by-step explanation:
Answer: (A ) greater than
Step-by-step explanation:
The answer is greater than the number Of points Luther scores in each game
All you have to do is count the little lines and wherever the little end part of the line in box ends is the number of points he gets a game so Nelson is 24 points and Luther is 19 points.
will the sampling distribution of x always be approximately normally distributed? Explain. Choose the correct answer below 0 ?. Yes, because the Central Limit Theorem states that the sampling distribution of x is always approximately normally distributed O B. No, because the Central Limit Theorem states that the sampling distribution of x is approximately normally distributed only if the sample size is large enough O C. No, because the Central Limit Theorem states that the sampling distribution of x is approximately normally distributed only if the population being sampled is normally distributed O D No, because the Central Limit Theorem states that the sampling d bution of x is approximately no aly distribui d only i the sa le sae is mere than 5% f the p pat Click to select your answer 888 a 8 7 3 4 5 6 8 9 2
Answers
The correct answer is C. No, because the Central Limit Theorem states that the sampling distribution of x is approximately normally distributed only if the population being sampled is normally distributed.
The Central Limit Theorem (CLT) is a statistical principle that states that the sampling distribution of the mean of a sufficiently large sample from any population, regardless of the population's distribution shape, will be approximately normally distributed.
However, the CLT does not guarantee that the individual variable or the sampling distribution of a different statistic (such as the sum or the variance) will be normally distributed. The underlying population needs to be approximately normally distributed for the sampling distribution to also be approximately normal.
Therefore, the statement that the sampling distribution of x is always approximately normally distributed is not accurate. It is only approximately normal if the population being sampled is normally distributed or the sample size is large enough (due to the Central Limit Theorem).
For more details about Central Limit Theorem
https://brainly.com/question/898534
#SPJ4
Suppose x is a normally distributed random variable with
μ=14 and σ=2.
Find each of the following probabilities.
a. P(x≥14.5)
b. P(x≤13)
c. P(15.56≤x≤18.8)
d. P(9.5≤x≤17)
Answers
Given: μ=14 and σ=2. We have to find the following probabilities: a. P(x≥14.5) b. P(x≤13) c. P(15.56≤x≤18.8) d. P(9.5≤x≤17) Given, μ=14 and σ=2.
Therefore, P(9.5 ≤ x ≤ 17) = 0.921
Therefore, Z= (x - μ)/σ can be used to calculate the standard normal probabilities, where Z is a standard normal random variable. Since we don't know the value of x, we will use the Z-distribution for the following calculations.a) P(x ≥ 14.5) Now, Z = (x - μ)/σ
= (14.5 - 14)/2
= 0.25 \
Using Z-table, the area to the left of Z = 0.25 is 0.5987 P(x ≥ 14.5)
= 1 - P(x < 14.5)
= 1 - 0.5987
= 0.4013
Therefore, P(x ≥ 14.5) = 0.4013b) P(x ≤ 13)
Now, Z = (x - μ)/σ= (13 - 14)/2= -0.5
Using Z-table, the area to the left of Z = -0.5 is 0.3085P(x ≤ 13)= 0.3085
Therefore, P(x ≤ 13) = 0.3085c) P(15.56 ≤ x ≤ 18.8)
Now, Z1= (15.56 - μ)/σ= (15.56 - 14)/2= 0.78Z2= (18.8 - μ)/σ= (18.8 - 14)/2= 2.4
Using Z-table, the area to the left of Z = 0.78 is 0.7823
Therefore, P(15.56 ≤ x ≤ 18.8)= P(z < 2.4) - P(z < 0.78)= 0.9918 - 0.7823= 0.2095
Therefore, P(15.56 ≤ x ≤ 18.8) = 0.2095d) P(9.5 ≤ x ≤ 17)
Now, Z1= (9.5 - μ)/σ= (9.5 - 14)/2= -2.25Z2= (17 - μ)/σ= (17 - 14)/2= 1.5
Using Z-table, the area to the left of Z = -2.25 is 0.0122
The area to the left of Z = 1.5 is 0.9332
To know more about probabilities visit:
https://brainly.com/question/29381779
#SPJ11
The function C(t) = 25.50t - 16.75 represents the cost of buying a certain number of
tickets to the concert with a $16.75 coupon. The cost, C, is measured in dollars for t
tickets.
1. Find the value of C(4).
2.What does C(4) represent in the context of the problem?
3.Is the value of C(6.5) reasonable to interpret in the context of the problem?
Answers
Answer: 85.25
Step-by-step explanation:

When you design an algorithm, it should be general enough to provide a solution to many problem instances, not just one or a few of them.T/F?
Answers
It is true that when you design an algorithm, it should be general enough to provide a solution to many problem instances, not just one or a few of them.
In mathematics, an algorithm is a process, a description of a series of steps that may be used to solve a problem; however, they are now far more prevalent than that.
Although many areas of research (and daily life) employ algorithms, long division's step-by-step process is probably the most prevalent example.
Thus, It is true that when you design an algorithm, it should be general enough to provide a solution to many problem instances, not just one or a few of them.
To know more about algorithm visit: brainly.com/question/29289479
#SPJ4
I need help on this math problem

Answers
Answer:
y= −1/2x + 3/4
Step-by-step explanation:
Write in slope-intercept form, y=mx +b.
Problem: 6x+12y=9
Hopefully this helps you!
Still stuck? Get 1-on-1 help from an expert tutor now.
Write the zero that corresponds to the factor (10x-9)
pls put step by step explanation thank you!!
Answers
Answer: The answer is 1x
Step-by-step explanation: Because It has (10x-9) Just Subtracted
can some one help me pleaseeee :(

Answers
a) 5/8
b) 3/5
Hope this helps
After sitting on a shelf for a while, a can of soda at a room temperature (73°F) is
placed inside a refrigerator and slowly cools. The temperature of the refrigerator is
39°F. Newton's Law of Cooling explains that the temperature of the can of soda will
decrease proportionally to the difference between the temperature of the can of soda
and the temperature of the refrigerator, as given by the formula below:
T=Ta +(To-Ta)e-kt
The can of soda reaches the temperature of 61°F after 15 minutes. Using this
information, find the value of k, to the nearest thousandth. Use the resulting
equation to determine the Fahrenheit temperature of the can of soda, to the nearest
degree, after 115 minutes.
Enter only the final temperature into the input box.
Answers
Therefore, the temperature of the can of soda after 115 minutes is approximately 55°F, rounded to the nearest degree.
What purpose does a mathematical equation serve?A mathematical equation is an expression with equality on both sides of the equal to sign that connects two other expressions. Think about the equation 3y = 16 as an illustration.
To find the value of k, we need to use the information given to solve for k in the equation T = Ta + (To - Ta) * \(e^(-kt)\), where T is the temperature of the can of soda, Ta is the ambient temperature (73°F), To is the temperature of the refrigerator (39°F), and t is the time elapsed in minutes.
We know that after 15 minutes, the temperature of the can of soda reaches 61°F, so we can substitute these values into the equation and solve for k:
61 = 73 + (39 - 73) * \(e^(-k * 15)\)
-12 = -34 * \(e^(-15k)\)
0.3529 =\(e^(15k)\)
㏒(0.3529) = 15k
k = -0.0301
So k is approximately -0.0301, rounded to the nearest thousandth.
To find the temperature of the can of soda after 115 minutes, we can use the same equation with the value of k we just found:
T = 73 + (39 - 73) * \(e^(-0.0301 * 115)\)
T = 73 + (-34) * \(e^(-3.47)\)
T = 73 + (-34) * 0.54
T = 54.62
Therefore, the temperature of the can of soda after 115 minutes is approximately 55°F, rounded to the nearest degree.
To know more about equation visit:
https://brainly.com/question/10413253
#SPJ1
Which of the following points are in the second quadrant of the xy plane?
Check all that apply.
A. (6, -2)
B. (-2, -8)
C. (-7, 6)
D. (2,2)
E. (-4, 2)
F. (4,8)
Answers
Answer:
a
Step-by-step explanation:
Answer: a and b bc that are in the negative-positive quad
The quadrants go in the order of the letter c so quadrant one is top right, while quadrant four is bottom right :)
22/11,594 I need a step by step answer
Answers
Answer:
1.89753
Step-by-step explanation:
22/11,594
Multiply the numerator and denominator by 1000 to remove decimal\(\frac{22}{11.594} * 1000 = \frac{22000}{11594}\)
Using long divisionLearn more about Long Division here: https://brainly.com/question/12085148