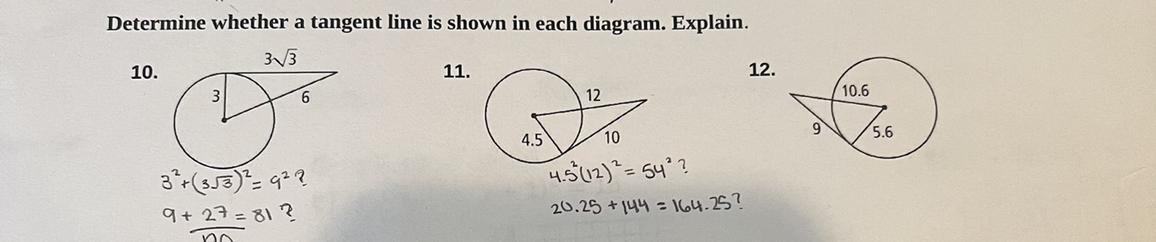determine whether number 12 has a tangent line shown in the diagram

The value of the required missing angle is;

m<JKM = 35°

We know from geometry that the sum of angles in a triangle sums up to 180 degrees.

Now, we are trying told that in the given Triangle that the angle m<J = 55 degrees.

We also see that the angle <KMJ is equal to 90 degrees becasue it is a right angle.

Thus to find the angle m<JKM, we can write the name expression as;

m<JKM = 180 - (90 + 55)

m<JKM = 35°

Thus that's the value of the required missing angle.

Read more about Missing angle at: https://brainly.com/question/28293784

#SPJ1

Using L'hopital we can see that the limit is equal to 1/22

Here we want to take the limit of x tending to zero for x/sin(22x)

Notice that when x = 0, both numerator and denominator are zero, so we need to take the limit of the first derivatives, for:

y = x

y' = 1

And for:

y = sin(22x)

y' = 22*cos(22x)

Now taking the limit we will get:

\(\lim_{x \to 0} \frac{1}{22cos(22x)} = \frac{1}{22cos(0)} = 1/22\)

That is the value of the limit.

Learn more about limits at.

https://brainly.com/question/5313449

#SPJ1

The maximum acceleration attained on the interval [0,3] by the particle whose velocity is given by: v(t) = t3 – 3t2 + 12t + 4 is 21

The correct answer is an option (a)

The velocity function is given by,

v(t) = t³ – 3t² + 12t + 4

We differentiate above function to get the acceleration function which will be

a(t) = v'(t)

a(t) = 3t² - 6t + 12 + 0

a(t) = 3t² - 6t + 12

Consider the interval [0,3]

We find the value of acccleration function at the end of the intervals.

For t = 0,

a(0) = 3(0)² - 6(0) + 12

a(0) = 0 - 0 + 12

a(0) = 12

And for t = 3,

a(3) = 3(3)² - 6(3) + 12

a(3) = 27 - 18 + 12

a(3) = 21

This means, the function a(t) is increasing and the maximum value of function a(t) would be at t = 3.

Therefore, the maximum acceleration attained on the interval [0,3] is 21

Learn more about the function here:

https://brainly.com/question/28193995

#SPJ4

Answer: a < -2

Step-by-step explanation:

a - 2 < -4

a < -4 + 2

a < -2

The domain and the range of the piecewise function in this problem are given as follows:

The function in this problem is defined for all values of x between -6 and 2, except x = 0, and assumes all values of y between 0 and 6, except y = 1, hence the domain and range are given as follows:

Learn more about domain and range at https://brainly.com/question/26098895

#SPJ1

The missing value in the table include the following: B. 4 1/2 in.

In Mathematics and Geometry, the volume of a rectangular prism can be calculated by using the following formula:

Volume of a rectangular prism = L × W × H

Where:

By substituting the given dimensions (parameters) into the formula for the volume of a rectangular prism, we have;

50 5/8 = 5 × W × 2 1/4

Width, W = 4 1/2 inches.

Read more on volume of prism here: brainly.com/question/21012007

#SPJ1

Complete Question:

The volume of a rectangular prism is 50 5/8 cubic inches.

The dimensions are given below.

What is the missing value in the table?

Length Width Height

5 in. 214 in.

A. 79in.

B. 412in.

C. 134in.

D. 1018in.

Answer: 615.44 m^3.

Step-by-step explanation: To find the volume of a cone, you need to multiply the radius, pi, and height.  The equation is given below:

π x r^2 x h = V, where π is pi, r is the radius squared, h is the height, and V is the volume.

Now, we need to substitute the values with the information that is given.  π ≈ 3.14:

3.14 x 7^2 x 12 ≈ 1846.32.

We are not finished yet!  A cone's volume is a third of a cylinder's, so you need to split 1846.32 in 1/3:

1/3 x 1846.32 ≈ 615.44 m^3.

Hope this helps! :)

Hi ;-)

Calculate

\(6-(-11)=6+11=\boxed{17}\)

Answer:

17

Step-by-step explanation:

6-(-11)

Subtracting a negative is like adding

6+11

17

Answer:

(3x+2)(x-5)

Step-by-step explanation:

Factor by grouping

\(3x^2-13x-10\\=3x^2-15x+2x-10\\=3x(x-5)+2(x-5)\\=(3x+2)(x-5)\)

Answer:

Consistent and Independent System

Step-by-step explanation:

A system with at least one solution is a consistent system.  A consistent system is said to be independent if it has exactly one solution (often referred to as the unique solution).  The graphs intersect at exactly one point, which gives an ordered-pair (x, y) as the solution of the system.  

Therefore , the solution of the given problem of equation comes out to be factor is (5b)(-5b+3).

A formula for connecting two statements using the equal sign (=) to denote equivalence is known as a mathematical equation. A mathematical equation in algebra is a statement that proves the equality of two mathematical expressions. For instance, the formula 3x + 5 = 14 places an equal sign between the variables 3x + 5 and 14. The mathematical relationship between the two sentences on either side of a letter is established. Most of the time, the symbol serves as both the one and only variable. for instance, 2x – 4 = 2.

Here,

the two numbers' primary factors are as follows:

-25\(b^{2}\) + 15b

Common prime factors can be multiplied to determine the GCF:

=> -25\(b^{2}\)  = -(5)(5) * \(b^{2}\)

=> 15b = (5)(3)b

The expression can be factored in the following fashion because the GCF is 5b:

=> -(5)(5) * \(b^{2}\) +  (5)(3)b

=> (5b)(-5b+3)

Therefore , the solution of the given problem of equation comes out to be factor is (5b)(-5b+3).

To know more about equation visit:

https://brainly.com/question/649785

#SPJ1

Answer:

x=-5, y=-1

Step-by-step explanation:

Answer:

Input complete question please.

Answer:

5x-7

Step-by-step explanation:

Question 3)

Given

The point (1, -5)

The slope m = -5/6

Using the point-slope form of the equation of a line

\(y-y_1=m\left(x-x_1\right)\)

where

In our case:

substituting the values m = -5/6 and the point (1, -5) in the point-slope form of the equation of the line

\(y-y_1=m\left(x-x_1\right)\)

\(y-\left(-5\right)=-\frac{5}{6}\left(x-1\right)\)

\(y+5=-\frac{5}{6}\left(x-1\right)\)

Thus, the point-slope form of the equation of the line is:

\(y+5=-\frac{5}{6}\left(x-1\right)\)

Question 4)

Given

The point (-1, 5)

The slope m = -7/2

In our case:

substituting the values m = -7/2 and the point (-1, 5) in the point-slope form of the equation of the line

\(y-y_1=m\left(x-x_1\right)\)

\(y-5=-\frac{7}{2}\left(x-\left(-1\right)\right)\)

\(y-5=-\frac{7}{2}\left(x+1\right)\)

Thus, the point-slope form of the equation of the line is:

\(y-5=-\frac{7}{2}\left(x+1\right)\)

Answer:

3*3

Step-by-step explanation:

hope it helps you

thank you

Answer:

0.4636 radians

Step-by-step explanation:

To find theta in radians, we need to use the inverse tangent function, also known as arctangent. From the right triangle in the image, we have:

tangent(theta) = opposite/adjacent = 10/20 = 1/2

Taking the inverse tangent of both sides, we get:

theta = arctan(1/2)

Using a calculator or a trigonometric table, we find:

theta ≈ 0.4636 radians

Therefore, theta is approximately 0.4636 radians

The results of the binary operators are listed below:

According to function theory, addition and subtraction are binary operators done between two functions, which are defined below:

(f + g) (x) = f (x) + g (x)               (1)

(f - g) (x) = f (x) - g (x)                 (2)

If we know that p(x) = 9 · x⁵ - 6 · x³ + 2 · x², q(x) = 7 · x⁴ - 3 · x³ - x² + 5 and r(x) = 2 · x² + 5 · x⁴ - x + 6, then the following expressions are obtained:

p(x) + q(x) = (9 · x⁵ - 6 · x³ + 2 · x²) + (7 · x⁴ - 3 · x³ - x² + 5)

p(x) + q(x) = 9 · x⁵ + 7 · x⁴ + (- 6 · x³ - 3 · x³) + (2 · x² - x²) + 5

p(x) + q(x) = 9 · x⁵ + 7 · x⁴ - 9 · x³ + x² + 5

q(x) - r(x) = (7 · x⁴ - 3 · x³ - x² + 5) - (2 · x² + 5 · x⁴ - x + 6)

q(x) - r(x) = (7 · x⁴ - 3 · x³ - x² + 5) + (- 1) · (2 · x² + 5 · x⁴ - x + 6)

q(x) - r(x) = (7 · x⁴ - 3 · x³ - x² + 5) + [(- 1) · (2 · x²) + (- 1) · (5 · x⁴) + (- 1) · (- x) + (- 1) · 6]

q(x) - r(x) = (7 · x⁴ - 3 · x³ - x² + 5) + (- 2 · x² - 5 · x⁴ + x - 6)

q(x) - r(x) = (7 · x⁴ - 5 · x⁴) - 3 · x³ + (- x² - 2 · x²) + x + (5 - 6)

q(x) - r(x) = 2 · x⁴ - 3 · x³ - 3 · x² + x - 1

p(x) - r(x) = (9 · x⁵ - 6 · x³ + 2 · x²) - (2 · x² + 5 · x⁴ - x + 6)

p(x) - r(x) = (9 · x⁵ - 6 · x³ + 2 · x²) + (- 1) · (2 · x² + 5 · x⁴ - x + 6)

p(x) - r(x) = (9 · x⁵ - 6 · x³ + 2 · x²) + [(- 1) · (2 · x²) + (- 1) · (5 · x⁴) + (- 1) · (- x) + (- 1) · 6]

p(x) - r(x) = (9 · x⁵ - 6 · x³ + 2 · x²) + (- 2 · x² - 5 · x⁴ + x - 6)

p(x) - r(x) = 9 · x⁵ - 5 · x⁴ - 6 · x³ + (2 · x² - 2 · x²) + x - 6

p(x) - r(x) = 9 · x⁵ - 5 · x⁴ - 6 · x³ + x - 6

r(x) - q(x) = (2 · x² + 5 · x⁴ - x + 6) - (7 · x⁴ - 3 · x³ - x² + 5)

r(x) - q(x) = (2 · x² + 5 · x⁴ - x + 6) + (- 1) · (7 · x⁴ - 3 · x³ - x² + 5)

r(x) - q(x) = (2 · x² + 5 · x⁴ - x + 6) + [(- 1) · (7 · x⁴) + (- 1) · (- 3 · x³) + (- 1) · (- x²) + (- 1) · 5]

r(x) - q(x) = (2 · x² + 5 · x⁴ - x + 6) + (- 7 · x⁴ + 3 · x³ + x² - 5)

r(x) - q(x) = (5 · x⁴ - 7 · x⁴) + 3 · x³ + (2 · x² + x²) - x + (6 - 5)

r(x) - q(x) = - 2 · x⁴ + 3 · x³ + 3 · x² - x + 1

To learn more on functions: https://brainly.com/question/12431044

#SPJ1

Answer:

1) x = 6

2) 129

Step-by-step explanation:

For equation 1:

\(7x=42\\\\\frac{7x=42}{7}\\\\ \boxed{x=6}\)

Expression 2:

Apply PEMDAS Rule.

\(8^2+9((12/3)*2)-7\\\\8^2+9(4*2)-7\\\\8^2+9(8)-7\\\\64+9(8)-7\\\\64+72-7\\\\136-7\\\\\boxed{129}\)

Hope this helps.

Answer:

It takes Jane 2 2/3 minutes

It takes Joan 5 1/3 minutes

Step-by-step explanation:

let j = time it takes Jane

let 2j = time it take Joan

j + 2j = 8

3j = 8

j = 8/3 or 2/23

2j = 16/3 or 5 1/3

Answers:

==========================================

Explanation:

Answer: 0.07

Step-by-step explanation:

To find the relative frequency of people in the sample whose place of residence is suburban and whose highest degree is a two-year degree, we need to calculate the ratio of the number of people with those characteristics to the total sample size.

Looking at the contingency table, we can see that the number of people in the suburban category with a two-year degree is 21.

The total sample size is given as 311.

Therefore, the relative frequency can be calculated as:

Relative frequency = (Number of people in suburban category with two-year degree) / (Total sample size)

= 21 / 311

≈ 0.0676

Rounded to two decimal places, the relative frequency is approximately 0.07.

The value of y in simplest form for the point P = (1/2, y) lying on the unit circle is y = ± √(3)/2.

To find the value of y in simplest form for the point P = (1/2, y) lying on the unit circle, we can use the equation of the unit circle, which states that for any point (x, y) on the unit circle, the following equation holds: x^2 + y^2 = 1.

Plugging in the coordinates of the point P = (1/2, y), we get:

(1/2)^2 + y^2 = 1

1/4 + y^2 = 1

y^2 = 1 - 1/4

y^2 = 3/4.

To simplify y^2 = 3/4, we take the square root of both sides:y = ± √(3/4).

Now, we need to simplify √(3/4). Since 3 and 4 share a common factor of 1, we can simplify further: y = ± √(3/4) = ± √(3)/√(4) = ± √(3)/2.

for more search question point  

https://brainly.com/question/28162977

#SPJ8

The answer would be 30 because the triangle is 10, the circle is 5, and each black triangle is 2 which would be 10 plus 5 which is 15 then times 2 which is 30.

Answer:

20?

Step-by-step explanation:

If 3 triangles = 30 they we could assume that each triangle = 10

10 + 10 + 10 = 30

If one triangle = 10 then the 2 circles would = 5 in the 2nd equation

10 + 5 + 5 = 20

If 1 circle = 5 then the 1 full squares would = 4

5 + 4 + 4 = 13

1 triangle = 10 , 1 circle = 5, Half a square = 2

10 + 5 * 2 = ?

Using PEMDAS we would multiply 2 and 5 first to get 10

10 + 10 = 20

The trigonometric equations has the following solutions: x = 0 + j · π or x = 0.352π + j · π or x = - 0.352π + j · π, where j is a non-negative whole number.

In this problem we find the case of a trigonometric equation, whose solutions on the interval [0, 2π] must be found. This can be done by both algebra properties and trigonometric formulae. First, write the entire expression:

tan² x · sec² x + 2 · sec² x - tan² x = 2

Second, use trigonometric formulas to reduce the number of trigonometric functions:

tan² x · (tan² x + 1) + 2 · (tan² x + 1) - tan² x = 2

Third, expand the equation:

tan⁴ x + tan² x + 2 · tan² x + 2 - tan² x = 2

tan⁴ x + 2 · tan² x = 0

Fourth, factor the expression:

tan² x · (tan² x - 2) = 0

tan² x = 0 or tan² x = 2

tan x = 0 or tan x = ± √2

Fifth, determine the solutions to trigonometric equation:

x = 0 + j · π or x = 0.352π + j · π or x = - 0.352π + j · π, where j is a non-negative whole number.

To learn more on trigonometric equations: https://brainly.com/question/22624805

#SPJ1

All the points (20, -2), (-2, 2), (4, 2), (8, 1), (-8, 5), and (16, -1) lie on the same line.

To determine which points lie on the same line passing through (-4, 4) and (12, 0), we can use the equation of a line.

First, we find the slope (m) of the line using the formula:

m = (y2 - y1) / (x2 - x1),

where (x1, y1) and (x2, y2) are the coordinates of the two given points.

m = (0 - 4) / (12 - (-4)) = -4 / 16 = -1/4.

Now that we have the slope, we can use the point-slope form of a linear equation:

y - y1 = m(x - x1),

where (x1, y1) is any point on the line.

Let's check which points satisfy this equation:

(20, -2):

-2 - 4 = (-1/4)(20 - (-4)),

-6 = (-1/4)(24),

-6 = -6.

The equation is true, so (20, -2) lies on the same line.

(-2, 2):

2 - 4 = (-1/4)(-2 - (-4)),

-2 = (-1/4)(2),

-2 = -2.

The equation is true, so (-2, 2) lies on the same line.

(4, 2):

2 - 4 = (-1/4)(4 - (-4)),

-2 = (-1/4)(8),

-2 = -2.

The equation is true, so (4, 2) lies on the same line.

(8, 1):

1 - 4 = (-1/4)(8 - (-4)),

-3 = (-1/4)(12),

-3 = -3.

The equation is true, so (8, 1) lies on the same line.

(-8, 5):

5 - 4 = (-1/4)(-8 - (-4)),

1 = (-1/4)(-4),

1 = 1.

The equation is true, so (-8, 5) lies on the same line.

(16, -1):

-1 - 4 = (-1/4)(16 - (-4)),

-5 = (-1/4)(20),

-5 = -5.

The equation is true, so (16, -1) lies on the same line.

In summary, all of the given points: (20, -2), (-2, 2), (4, 2), (8, 1), (-8, 5), and (16, -1) lie on the same line passing through the points (-4, 4) and (12, 0).

For more question on  points visit:

https://brainly.com/question/23848540

#SPJ8

Note the complete question is

A line passes through the points (-4, 4) and (12, 0) . Which points lie on the same line? Select all that apply: (20_ -2) (-2, 2) (4, 2) (8, 1) (-8, 5) (16, -1)

Answer:

x = ± 10

Step-by-step explanation:

- 5x² = - 500 ( divide both sides by - 5 )

x² = 100 ( take square root of both sides )

x = ± \(\sqrt{100}\) = ± 10

That is x = - 10 or x = 10

Answer:

a. In the explanation.

b. The point estimate of the difference can be calculated as the difference between the sample mean and the population mean:

\(d=M-\mu=24.95-23.8=1.15\)

c. Test statistic t = 0.90

P-value = 0.1932

The null hypothesis failed to be rejected.

Step-by-step explanation:

We have a sample, wich mean and standard deviation are calculated as:

\(M=\dfrac{1}{14}\sum_{i=1}^{14}(27.8+23.84+25.25+21+17.52+19.61+...+26.94+27.24)\\\\\\ M=\dfrac{349.34}{14}=24.95\)

\(s=\sqrt{\dfrac{1}{(n-1)}\sum_{i=1}^{14}(x_i-M)^2}\\\\\\s=\sqrt{\dfrac{1}{13}\cdot [(27.8-(24.95))^2+(23.84-(24.95))^2+...+(27.24-(24.95))^2]}\\\\\\s=\sqrt{\dfrac{1}{13}\cdot [(8.106)+(1.238)+...+(5.23)]}\\\\\\ s=\sqrt{\dfrac{304.036}{13}}=\sqrt{23.39}\\\\\\s=4.8\)

This is a hypothesis test for the population mean.

The claim is that the consumption of milk in the Midwest is significantly higher than the national average.

Then, the null and alternative hypothesis are:

\(H_0: \mu=23.8\\\\H_a:\mu> 23.8\)

The significance level is 0.01.

The sample has a size n=14.

The sample mean is M=24.95.

As the standard deviation of the population is not known, we estimate it with the sample standard deviation, that has a value of s=4.8.

The estimated standard error of the mean is computed using the formula:

\(s_M=\dfrac{s}{\sqrt{n}}=\dfrac{4.8}{\sqrt{14}}=1.28\)

Then, we can calculate the t-statistic as:

\(t=\dfrac{M-\mu}{s/\sqrt{n}}=\dfrac{24.95-23.8}{1.28}=\dfrac{1.15}{1.28}=0.9\)

The degrees of freedom for this sample size are:

\(df=n-1=14-1=13\)

This test is a right-tailed test, with 13 degrees of freedom and t=0.9, so the P-value for this test is calculated as (using a t-table):

\(\text{P-value}=P(t>0.9)=0.1932\)

As the P-value (0.1932) is bigger than the significance level (0.01), the effect is not significant.

The null hypothesis failed to be rejected.

There is not enough evidence to support the claim that the consumption of milk in the Midwest is significantly higher than the national average.