Determine the volume of sphere with a radius of six inches. What is the volume of the sphere in terms of π?
Answers
Answer:
288π inch³
Step-by-step explanation:
V=4
/3πr³
by substituding in formulae
4/3*216π
=288π inch³
hope this helps
plzz mark me brainliest
Related Questions
a display at an aquarium has sea stars to wolf eels in a ratio 4 : 5. It also has 5/8 as many rockfish as sea stars. there are 40 more wolf eels than rock fish. How many sea stars are there?
Answers
The number of sea stars is 64.
What is a ratio?
Comparing two amounts of the same units and determining the ratio tells us how much of one quantity is in the other.
In general, a: b, which can be interpreted as "a is to b," is used to denote a ratio between two quantities, let's say "a" and "b."
This ratio is expressed in fraction form as a/b. We utilize the same method for further simplifying a ratio as we use for further simplifying a fraction.
According to the question,
Ratio of sea stars to wolf eels = 4:5
Number of rock fish= 5/8 (Number of sea stars)
Number of wolf eels - Number of rock fish = 40
Using the given information, we get,
Number of sea stars = 8/5 (Number of rock fish)
On simplification,
Number of wolf eels = 80
So, number of sea stars = (4/5)*80
= 64
Learn more about ratios here:
https://brainly.com/question/2328454
#SPJ1
which methods correctly solve for the variable s in the equation -2 - 5s =9?

Answers
One number is 7 less than a second number.Twice the second number is 2 less than 4 time the first
Answers
what number represents the same amount as 2 hundreds + 12 tens + 6 ones ?
Answers
Answer:
326
Step-by-step explanation:
The value of the given expression is 326.
Given:
The given expression 2 hundreds + 12 tens + 6 ones.
To find:
The value of the given expression.
Explanation:
The numeric form of given expression is:
2 hundreds + 12 tens + 6 ones
2 hundreds + 12 tens + 6 ones
2 hundreds + 12 tens + 6 ones
Therefore, the value of the given expression is 326.
Write the equation of the line if the line passes through (4,4) and the y-intercept is -4.
•y = 2x - 4
•y = 2x - 2
•None of these answers are correct.
•y = 8x + 4
•y = 2x + 4
Answers
Answer:
y = 2*x - 4
Step-by-step explanation:
The general equation for a line is:
y = a*x + b
Where a is the slope and b is the y-intercept.
In this case, we know that the line passes through (4, 4) and the y-intercept is -4.
Then:
b = -4
So our line is something like:
y = a*x - 4
Now, we know that the line passes through (4, 4), which means that when x = 4, y = 4.
If we replace these values in the equation, we get:
4 = a*4 - 4
Now we can solve this for a.
4 = a*4 - 4
4 + 4 = a*4
8 = a*4
8/4 = a = 2
Then the equation for the line is:
y = 2*x - 4
Isaiah spent $19.60 on a gift for his mother. The amount that he spent on the gift was StartFraction 5 over 7 EndFraction of the total amount that he spent at the store.
Which statements can be used to find x, the total amount that Isaiah spent at the store? Select three options.
Answers
Answer:
It's B, C, and E on Edge2020. I took the Unit Test Review and I was right.
The total amount that Isaiah spent at the store is $27.44.
Given that, Isaiah spent $19.60 on a gift for his mother.
Let the total amount be x.
What is an equation?A statement that the values of two mathematical expressions are equal (indicated by the sign =).
The amount that was spent on gifts was 5/7 of the total amount.
Now, 5/7×x=19.60
⇒x=$27.44
Therefore, the total amount that Isaiah spent at the store is $27.44.
To learn more about the fractions visit:
https://brainly.com/question/10354322.
#SPJ5
This figure represents a compartment in a container for storing craft supplies. Another compartment is identical except that it is 4 centimeters taller.
What is the difference in volume of the two compartments?

Answers
The difference in volume between the two compartments is given as follows:
346.4 cm³.
How to obtain the volume of the prism?The volume of a prism is obtained as the multiplication of the area of the base of the prism by the height of the prism, as follows:
The height of the base of the prism in this problem is given as follows:
h² + 5² = 10²
\(h = \sqrt{10^2 - 5^2}\)
h = 8.66.
Hence the base is composed as follows:
Rectangle of dimensions 5 cm and 8.66 cm.Two right triangles of sides 5 cm and 8.66 cm.Hence the base area is given as follows:
Ab = 5 x 8.66 + 2 x 1/2 x 5 x 8.66
Ab = 86.6 cm².
The height is given as follows:
7 cm.
Hence the volume is:
7 x 86.6 = 606.2 cm³.
The height of the taller prism is given as follows:
11 cm.
Hence the volume is:
11 x 86.6 = 952.6 cm³.
Hence the difference of volumes is of:
952.6 - 606.2 = 346.4 cm³.
More can be learned about the volume of a prism at https://brainly.com/question/23766958
#SPJ1
Can I please get some help I’ve been stuck on this question for a while!

Answers
Using the radius of the Ferris wheel and the angle between the two positions, the time spent on the ride when they're 28 meters above the ground is 12 minutes
How many minutes of the ride are spent higher than 28 meters above the ground?The radius of the Ferris wheel is 30 / 2 = 15 meters.
The highest point on the Ferris wheel is 15 + 4 = 19 meters above the ground.
The time spent higher than 28 meters is the time spent between the 12 o'clock and 8 o'clock positions.
The angle between these two positions is 180 degrees.
The time spent at each position is 10 minutes / 360 degrees * 180 degrees = 6 minutes.
Therefore, the total time spent higher than 28 meters is 6 minutes * 2 = 12 minutes.
Learn more on a Ferris wheel here;
https://brainly.com/question/30524034
#SPJ1
A tank is full of water. Find the work (in ft-lb) required to pump the water out of the spout. Use the fact that water weighs 62.5 lb/ft3. (Round your answer to the nearest whole number.) 3 ft6 ft12 ft A frustum of a cone with a spout is given. The smaller radius is 3 ft, the larger radius is 6 ft, and the height is 12 ft.
Answers
The work required to pump the water out of the spout is approximately 64,307,077 ft-lb
To find the work required to pump the water out of the spout, we need to calculate the weight of the water in the tank and then convert it to work using the formula: work = force × distance.
First, let's calculate the volume of water in the tank. The frustum of a cone can be represented by the formula: V = (1/3)πh(r1² + r2² + r1r2), where r1 and r2 are the radii of the two bases and h is the height.
Given r1 = 3 ft, r2 = 6 ft, and h = 12 ft, we can calculate the volume:
V = (1/3)π(12)(9 + 36 + 18) = 270π ft³
Now, we can calculate the weight of the water using the density of water:
Weight = density × volume = 62.5 lb/ft³ × 270π ft³ ≈ 53125π lb
Next, we convert the weight to force by multiplying it by the acceleration due to gravity (32.2 ft/s²):
Force = Weight × acceleration due to gravity = 53125π lb × 32.2 ft/s² ≈ 1709125π lb·ft/s²
Finally, we can calculate the work by multiplying the force by the distance. Since the water is being pumped out of the spout, the distance is equal to the height of the frustum, which is 12 ft:
Work = Force × distance = 1709125π lb·ft/s² × 12 ft ≈ 20509500π lb·ft ≈ 64307077 lb·ft
for more search question water
https://brainly.com/question/17120212
#SPJ8
Given that Kelsey has already made 10 pendants how many additional pendants must she make and sell to make a profit of 50 dollars?
Answers
Part a: Kelsey should make 36 pendants
Part b: Kelsey needs to make 26 more pendants
Rent of the booth at the craft fair = $200
The material cost of each pendant = is $7.80
The selling cost of each pendant = is $13.50
Let Kelsey make x number of pendants
Formulating the inequality equation we get:
Selling cost of each pendant*Number of pendants >= Rent of the booth + Material cost of each pendant*Number of pendants
= 13.50x >= 200 + 7.80x
Solving the inequality we get:
13.50x >=200+7.80x
5.70x >= 200
x >= 35.08
So, she should make a total of 36 pendants
Considering that she has already made 10 pendants. She needs 26 more pendants.
Although a part of your question is missing, you might refer to this full question: Kelsey makes pendants that she would like to sell at an upcoming craft fair. She must pay $200 to rent a booth at the craft fair. The materials for each pendant cost $7.80, and she plans to sell each pendant for $13.50. To make a profit, she must make more money than she spends. Kelsey has already made 10 pendants. Part A: Write and solve an inequality to show how many pendants Kelsey should make. Show the steps of your solutions. Part B: Given that Kelsey has already made 10 pendants, how many additional pendants must she make and sell to make a profit?
Learn more about inequality:
https://brainly.com/question/20383699
#SPJ9
Felipe uploaded a funny viedo of his dog. The relationship between the elapsed time in days, d , since the viedo was first uploaded and the total number of views, v , that the viedo received is modeled by v=4^1.25d . Find the number of days it took Felipe's viedo to get 1024 views.
Answers
The number of days took to get the video of Felipe 1024 views is 4.
What is an Equation?An equation is the statement of two expressions located on two sides connected with an equal to sign. The two sides of an equation is usually called as left hand side and right hand side.
The relationship between the elapsed time in days, d, since the video was uploaded and the total number of views, v, that the video received is modeled by the equation,
v = 4^(1.25d)
We have to find d when v = 1024
1024 = 4^(1.25d)
We have the rule for exponents aᵇⁿ = (aᵇ)ⁿ
1024 = \((4^{1.25} )^d\)
1024 = (5.6569)^d
Taking logarithms on both sides,
㏒ (1024) = ㏒ [(5.6569)^d]
We have the exponent rule for logarithm, ㏒ (aᵇ) = b ㏒ (a)
㏒ (1024) = d ㏒ (5.6569)
d = ㏒ (1024) / ㏒ (5.6569)
d = 4
Hence it took 4 days to for Felipe's video to get 1024 views.
Learn more about Equations here :
https://brainly.com/question/22960530
#SPJ1
Enter the product as a product of a hole number and unit fraction. 2 x 5/4.
Answers
The rear windshield wiper of a car rotated 120 degrees,as shown. Find the area cleared by the wiper. 25inch,120 degrees, 14inch

Answers
The rear windshield wiper of a car rotated 120 degrees, as shown in the figure. The area cleared by the wiper blade is approximately 205.875 square inches.
The problem states that a car’s rear windshield wiper rotates 120 degrees, as shown in the figure. Our aim is to find the area cleared by the wiper.
The wiper's arm is represented by a line segment and has a length of 14 inches.
The wiper's blade is perpendicular to the arm and has a length of 25 inches.
Angular degree measure indicates how far around a central point an object has traveled, relative to a complete circle. A full circle is 360 degrees, and 120 degrees is a third of that.
As a result, the area cleared by the wiper blade is the sector of a circle with radius 25 inches and central angle 120 degrees.
The formula for calculating the area of a sector of a circle is: A = (θ/360)πr², where A is the area of the sector, θ is the central angle of the sector, π is the mathematical constant pi (3.14), and r is the radius of the circle.
In this situation, the sector's central angle θ is 120 degrees, the radius r is 25 inches, and π is a constant of 3.14.A = (120/360) x 3.14 x 25²= 0.33 x 3.14 x 625= 205.875 square inches, rounded to the nearest thousandth.
Therefore, the area cleared by the wiper blade is approximately 205.875 square inches.
For more such questions on area, click on:
https://brainly.com/question/25292087
#SPJ8
Factor Completely:
16x8−81y8
Answers
Answer:
Step-by-step explanation:
16x⁸ - 81y⁸ is the difference of squares.
16x⁸ - 81y⁸ = (4x⁴)² - (9y⁴)² = (4x⁴ + 9y⁴)(4x⁴ - 9y⁴)
Note that 4x⁴ - 9y⁴ is also the difference of squares.
4x⁴ - 9y⁴ = (2x²) - (3y²)² = (2x² + 3y²)(2x² - 3y²)
16x⁸ - 81y⁸ = (4x⁴ + 9y⁴)(2x² + 3y²)(2x² - 3y²)
I'll Give brainliest to whoever answers is correct
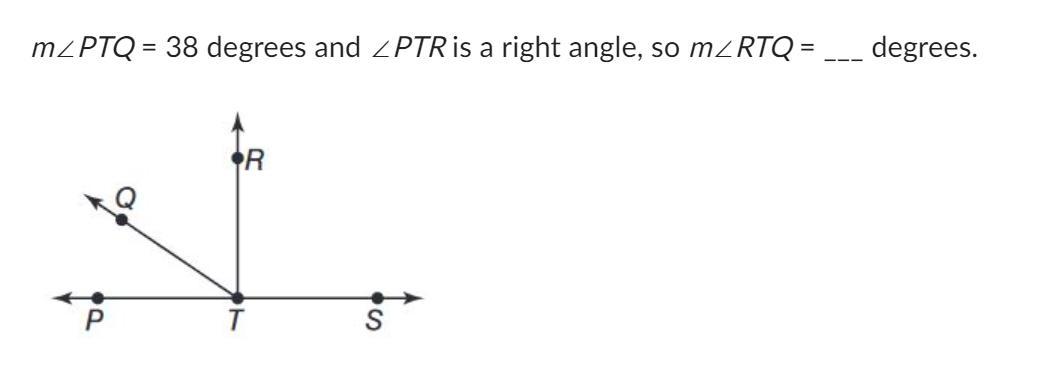
Answers
Answer:
52
Step-by-step explanation:
RTQ is 52 because if PTR is a right angle, right angles equal 90 degrees. So if PTQ is 38 degrees, we subtract 38 from 90 to get RTQ. 90-38 equals 52.
Answer:
52 degrees
Step-by-step explanation:
right angle = 90
90-38=52
So RTQ = 52 degrees
Non Shaded Shaded
Area
Area
8
Find the radius
of the small circle

Answers
Answer:
The answer is 16pi or 50.3cm² to 1 d.p
Step-by-step explanation:
The non shaded=area of shaded
d=8
r=d/2=4
A=pir³
A=p1×4²
A=pi×16
A=16picm² or 50.3cm² to 1d.p
Answer:
3.45 cm (3 s.f.)
Step-by-step explanation:
We have been given a 5-sided regular polygon inside a circumcircle. A circumcircle is a circle that passes through all the vertices of a given polygon. Therefore, the radius of the circumcircle is also the radius of the polygon.
To find the radius of a regular polygon given its side length, we can use this formula:
\(\boxed{\begin{minipage}{6 cm}\underline{Radius of a regular polygon}\\\\$r=\dfrac{s}{2\sin\left(\dfrac{180^{\circ}}{n}\right)}$\\\\\\where:\\\phantom{ww}$\bullet$ $r$ is the radius.\\ \phantom{ww}$\bullet$ $s$ is the side length.\\\phantom{ww}$\bullet$ $n$ is the number of sides.\\\end{minipage}}\)
Substitute the given side length, s = 8 cm, and the number of sides of the polygon, n = 5, into the radius formula to find an expression for the radius of the polygon (and circumcircle):
\(\begin{aligned}\implies r&=\dfrac{8}{2\sin\left(\dfrac{180^{\circ}}{5}\right)}\\\\ &=\dfrac{4}{\sin\left(36^{\circ}\right)}\\\\ \end{aligned}\)
The formulas for the area of a regular polygon and the area of a circle given their radii are:
\(\boxed{\begin{minipage}{6 cm}\underline{Area of a regular polygon}\\\\$A=\dfrac{nr^2\sin\left(\dfrac{360^{\circ}}{n}\right)}{2}$\\\\\\where:\\\phantom{ww}$\bullet$ $A$ is the area.\\\phantom{ww}$\bullet$ $r$ is the radius.\\ \phantom{ww}$\bullet$ $n$ is the number of sides.\\\end{minipage}}\)
\(\boxed{\begin{minipage}{6 cm}\underline{Area of a circle}\\\\$A=\pi r^2$\\\\where:\\\phantom{ww}$\bullet$ $A$ is the area.\\\phantom{ww}$\bullet$ $r$ is the radius.\\\end{minipage}}\)
Therefore, the area of the regular pentagon is:
\(\begin{aligned}\textsf{Area of polygon}&=\dfrac{5 \cdot \left(\dfrac{4}{\sin\left(36^{\circ}\right)}\right)^2\sin\left(\dfrac{360^{\circ}}{5}\right)}{2}\\\\&=\dfrac{5 \cdot \left(\dfrac{4}{\sin\left(36^{\circ}\right)}\right)^2\sin\left(72^{\circ}\right)}{2}\\\\&=\dfrac{\dfrac{80\sin\left(72^{\circ}\right)}{\sin^2\left(36^{\circ}\right)}}{2}\\\\&=\dfrac{40\sin\left(72^{\circ}\right)}{\sin^2\left(36^{\circ}\right)}\\\\&=110.110553...\; \sf cm^2\end{aligned}\)
The area of the circumcircle is:
\(\begin{aligned}\textsf{Area of circumcircle}&=\pi \left(\dfrac{4}{\sin\left(36^{\circ}\right)}\right)^2\\\\&=\dfrac{16\pi}{\sin^2\left(36^{\circ}\right)}\\\\&=145.489779...\; \sf cm^2\end{aligned}\)
The area of the shaded area is the area of the circumcircle less the area of the regular pentagon plus the area of the small central circle.
The area of the unshaded area is the area of the regular pentagon less the area of the small central circle.
Given the shaded area is equal to the unshaded area:
\(\begin{aligned}\textsf{Shaded area}&=\textsf{Unshaded area}\\\\\sf Area_{circumcircle}-Area_{polygon}+Area_{circle}&=\sf Area_{polygon}-Area_{circle}\\\\\sf 2\cdot Area_{circle}&=\sf 2\cdot Area_{polygon}-Area_{circumcircle}\\\\2\pi r^2&=2 \cdot \dfrac{40\sin\left(72^{\circ}\right)}{\sin^2\left(36^{\circ}\right)}-\dfrac{16\pi}{\sin^2\left(36^{\circ}\right)}\\\\2\pi r^2&=\dfrac{80\sin\left(72^{\circ}\right)}{\sin^2\left(36^{\circ}\right)}-\dfrac{16\pi}{\sin^2\left(36^{\circ}\right)}\\\\\end{aligned}\)
\(\begin{aligned}2\pi r^2&=\dfrac{80\sin\left(72^{\circ}\right)-16\pi}{\sin^2\left(36^{\circ}\right)}\\\\r^2&=\dfrac{40\sin\left(72^{\circ}\right)-8\pi}{\pi \sin^2\left(36^{\circ}\right)}\\\\r&=\sqrt{\dfrac{40\sin\left(72^{\circ}\right)-8\pi}{\pi \sin^2\left(36^{\circ}\right)}}\\\\r&=3.44874763...\sf cm\end{aligned}\)
Therefore, the radius of the small circle is 3.45 cm (3 s.f.).

A certain sum of money is divided among A, B, C in the ratio 2: 3 : 4. If A's share is RS. 20000, find the share of B and C.
Answers
Therefore, B's share is Rs. 30,000 and C's share is Rs. 40,000.
What is equation?An equation is a mathematical statement that shows that two expressions are equal. It consists of two parts: the left-hand side (LHS) and the right-hand side (RHS), separated by an equals sign (=). The equals sign indicates that the two expressions are equal, and the goal of solving the equation is to find the value of x that makes this statement true. Equations can be solved using various algebraic techniques, such as simplifying and rearranging the expressions, applying operations to both sides of the equation, and factoring or expanding expressions. Solving an equation involves finding the values of the variables that make the equation true.
Here,
Let the total sum of money be x.
Then, according to the given ratio, A's share is 2/9 of the total sum, so we have:
2/9 * x = 20000
Multiplying both sides by 9/2, we get:
x = 90000
Now, we can find the shares of B and C as follows:
B's share = 3/9 * 90000 = 30000
C's share = 4/9 * 90000 = 40000
To know more about equation,
https://brainly.com/question/2228446
#SPJ9
Write the algebraic equation for the following: The sum of 4 and another number is 22.
Answers
Answer:
\(4+x=22\)
Step-by-step explanation:
Hope this helps
X+4=22
Step-by-step explanation:
Let the other number= X
From the question
4+X= 22
X+4= 22
Suppose I am considering investing in a CD that pays an interest rate of 1.75%, compounded daily. To the nearest hundredth of a percent, what is the annual percentage yield on the CD?
Answers
Based on the interest rate and the period of compounding, the annual percentage yield on the CD would be 1. 77%
How to find the annualized return?The annualized return can be found by using the Effective Annual Rate (EAR) formula which is:
= ( 1 + annual rate / Compounding periods in a year) ^ number of compounding periods in a year - 1
Solving for the annual percentage yield is therefore:
= ( 1 + 1.75% / 365) ³⁶⁵ - 1
= 1.017654 - 1
= 0. 01765
= 1.77%
Find out more on annual percentage yield at https://brainly.com/question/27997520
#SPJ1
Which of the following shaded regions represents 1 the solution to the pair of inequalities y > 3 + 1 and y < 2? 2

Answers
To know which region is the solution to the pair of inequalities, we are going to graph the two lines first:
Since y<2, then the shaded region that represents the solutions is:
In the answer choices, the option E.


Write 3 numbers that are divisible by 2,
5, and 10.
Answers
Answer:A number is divisible by 2 if it ends in 2, 4, 6, 8 or 0. A number is divisible by 5 if it ends in 5 or 0. A number is divisible by 10 if it ends in a 0.Apr 8, 2018
Bree is climbing a mountain. She knows that the faster she climbs, the less time the climb will take.

Answers
We know that the faster she climbs, the less time the climb will take.
As you can observe, the given relationship is between her speed and the height of the climb. We can deduct that this situation can be modeled by the speed in function of the time.
However, let's analyze each answer choice.
Choice A can't be right because the height of the mountain is not variable, that is, the mountain won't change its height.
Choice B is relating time and speed which, as we said before, the situation involves a relationship between time and speed.
Therefore, the right answer is B.2c-10<3c-9 solve the following inequality
Answers
Answer:
\(c > -1\)
Step-by-step explanation:
\(2c-10 < 3c-9\\-10 < c-9\\-1 < c\\c > -1\)
I need h e l p
△ABC has a right angle at C, BC=9.2 centimeters, and m∠A=63∘.
What is CA ?
Enter your answer rounded to the nearest tenth in the box.
Answers
Answer:
17.8
Step-by-step explanation:
You have to add 9.2 and 63 and the subtract from 90. Hope this helped! <3
jalen drew a rectangle with a perimeter of 20 inches. the smaller side measured 3 inches. jalen said the longer side of the rectangle had to be 7 inches. is jalen correct?
Answers
Yes, Jalen is correct because the rectangle has a perimeter of 20 inches with the smaller side measuring 3 inches and the longer side of the rectangle had to be 7 inches.
How to calculate the perimeter of a rectangle?In Mathematics and Geometry, the perimeter of a rectangle can be calculated by using this mathematical equation (formula);
P = 2(L + W)
Where:
P represent the perimeter of a rectangle.W represent the width of a rectangle.L represent the length of a rectangle.By substituting the given side lengths into the formula for the perimeter of a rectangle, we have the following;
P = 2(3 + 7)
20 = 2(10)
20 = 20 (True).
Read more on perimeter of a rectangle here: brainly.com/question/28695033
#SPJ1
A 2100-square-foot home is for sale. The finished basement has an area of 455 square feet. The basement accounts for what percent of the total square footage?
Answers
Given the area of the house and the basement, the basement accounts for 21.67 percent of the total square footage.
What is Percentage?Percentage is simply number or ratio expressed as a fraction of 100.
It is expressed as;
Percentage = ( Part / Whole ) × 100%
Given that;
Area of the house = 2100ft²Area of the basement = 455ft²Percentage of area occupied by the basement = ?Percentage = ( Part / Whole ) × 100%
Percentage = ( 455ft² / 2100ft² ) × 100%
Percentage = 0.21666 × 100%
Percentage = 21.67%
Given the area of the house and the basement, the basement accounts for 21.67 percent of the total square footage.
Learn more about Percentages here: brainly.com/question/24159063
#SPJ1
use the binomial expansion
(a+b)⁴ = a⁴+4a³b+6a²b²+4ab³+b⁴ to expand and simplify (x-3)⁴
Answers
Answer:
\(x^4-12x^3+54x^2-108x+81\)
Step-by-step explanation:
We have been given the following binomial expansion for (a + b)⁴:
\(\boxed{(a+b)^4=a^4+4a^3b+6a^2b^2+4ab^3+b^4}\)
To use this to expand and simplify (x - 3)⁴, first identity the values of a and b:
a = xb = -3Substitute the values of a and b into the expansion, and simplify:
\(\begin{aligned}(x-3)^4&=x^4+4x^3(-3)+6x^2(-3)^2+4x(-3)^3+(-3)^4\\\\&=x^4+4x^3(-3)+6x^2(9)+4x(-27)+81\\\\&=x^4-12x^3+54x^2-108x+81\end{aligned}\)
Alessandra designed an experiment where subjects tasted water from four different cups and attempted to identify which cup contained bottled water. Each subject was given three cups that contained regular tap water and one cup that contained bottled water (the order was randomized). She wanted to test if the subjects could do better than simply guessing when identifying the bottled water.Her hypotheses were H0: p=0.25H vs.H a :p>0.25H,(where ppp is the true likelihood of these subjects identifying the bottled water).The experiment showed that 20 of the 60 subjects correctly identified the bottle water. Alessandra calculated that the statistic p=20, divided by, 60, 0.3 had an associated P-value of approximately 0.0680.What conclusion should be made using a significance level of α=0.05?A) Fail to reject H0B) Reject H0, and accept HaC) Accept H0
Answers
Answer:
3434
Step-by-step explanation:
The conclusion that should be made on the question using a significance level of α=0.05 is; Option A; Fail to reject H₀
We are given the hypotheses;
Null Hypothesis; H₀; p = 0.25
Alternative hypothesis; Hₐ; p > 0.25
p^ = 0.3
p-value = 0.068
Now, we are told that the significance level is α = 0.05
Now, the law in hypotheses testing is that when the p-value is less tan or equal to the significance level, we will reject the null hypothesis but when the p-value is greater than the significance value, we fail to reject the null hypothesis(H₀)
Now, in our question the p-value of 0.068 is greater than the significance level of 0.05 and thus we will fail to reject the null hypothesis.
Read more at; https://brainly.com/question/17128186
In which direction does the left side of the graph of this function point?f(x) = 3x3 - x2 + 4x - 2Answer hereSUBMIT
Answers
The given function is expressed as
f(x) = 3x^3 - x^2 + 4x - 2
This is a cubic function which also means that it is an odd function.
The graph of the function is shown below
A triangle LMN with ln = 12 cm,Nm= x cm, Nk = 6cm and Km 8cm
Calculate the value of
(i) x
(ii) o
Answers
The value of x is 9 cm, and angle O is 0 degrees.
To solve the triangle LMN and find the values of x and angle O, we can use the Law of Cosines and the Law of Sines. Let's go step by step:
(i) To find the value of x, we can use the Law of Cosines. According to the Law of Cosines, in a triangle with sides a, b, and c, and angle C opposite to side c, the following equation holds:
c^2 = a^2 + b^2 - 2ab * cos(C)
In our case, we want to find side NM (x), which is opposite to angle N. The given sides and angles are:
LN = 12 cm
NK = 6 cm
KM = 8 cm
Let's denote angle N as angle C, side LN as side a, side NK as side b, and side KM as side c.
Using the Law of Cosines, we can write the equation for side NM (x):
x^2 = 12^2 + 6^2 - 2 * 12 * 6 * cos(N)
We don't know the value of angle N yet, so we need to find it using the Law of Sines.
(ii) To find angle O, we can use the Law of Sines. According to the Law of Sines, in a triangle with sides a, b, and c, and angles A, B, and C, the following equation holds:
sin(A) / a = sin(B) / b = sin(C) / c
In our case, we know angle N and side NK, and we want to find angle O. Let's denote angle O as angle A and side KM as side b.
We can write the equation for angle O:
sin(O) / 8 = sin(N) / 6
Now, let's solve these equations step by step to find the values of x and angle O.
To find angle N, we can use the Law of Sines:
sin(N) / 12 = sin(180 - N - O) / x
Since we know that the angles in a triangle add up to 180 degrees, we can rewrite the equation:
sin(N) / 12 = sin(O) / x
Now, we can substitute the equation for sin(O) from the Law of Sines into the equation for sin(N):
sin(N) / 12 = (6 / 8) * sin(N) / x
Now, we can solve this equation for x:
x = (12 * 6) / 8 = 9 cm
So, the value of x is 9 cm.
To find angle O, we can substitute the value of x into the equation for sin(O) from the Law of Sines:
sin(O) / 8 = sin(N) / 6
sin(O) / 8 = sin(O) / 9
9 * sin(O) = 8 * sin(O)
sin(O) = 0
This implies that angle O is 0 degrees.
Therefore, the value of x is 9 cm, and angle O is 0 degrees.
For more questions on Law of Cosines, click on:
https://brainly.com/question/30766161
#SPJ8
The figure for the given question is provided here :
