Determine the value of y, if x = -3.
y = |x + |1|

Answer:

The value of y is 216

(and the value of x is 12)

Step-by-step explanation:

The general formula for a geometric sequence is,

\(a_n = a_1(r)^{n-1}\)

Where n represents the nth term, a_1 is the first term and r is the common ratio,

we see that,

r = 6,

the first term is,

a_1 = (x-6)

the 2nd term is,

a_2 = 3x,

the 3rd term is,

a_3 = y, finding y,

first we find x, using the above given formula we have,

\(a_2 = a_1(6)^{2-1}\\3x = (x-6)(6^1)\\3x = 6x -36\\36 = 6x - 3x\\36 = 3x\\x=36/3\\x=12\)

x = 12,

Now, for y we can use the relation between a_3 and a_2,

\(a_3 = a_1(6)^{3-1}\\y = (x-6)(6)^2\\y = (12-6)(6^2)\\y = 6(6^2)\\y = 6^3\\y = 216\)

y = 216

The temperature at the bottom of the mountain is 50.9 °C.

Let's work through the given information step by step to find the temperature at the bottom of the mountain.

The temperature in the hotel is 21 °C.

The temperature in the hotel is 26.7 °C warmer than at the top of the mountain.

Let's denote the temperature at the top of the mountain as T_top.

So, the temperature in the hotel can be expressed as T_top + 26.7 °C.

The temperature at the top of the mountain is 3.2 °C colder than at the bottom of the mountain.

Let's denote the temperature at the bottom of the mountain as T_bottom.

So, the temperature at the top of the mountain can be expressed as T_bottom - 3.2 °C.

Now, let's combine the information we have:

T_top + 26.7 °C = T_bottom - 3.2 °C

To find the temperature at the bottom of the mountain (T_bottom), we need to isolate it on one side of the equation. Let's do the calculations:

T_bottom = T_top + 26.7 °C + 3.2 °C

T_bottom = T_top + 29.9 °C

Since we know that the temperature in the hotel is 21 °C, we can substitute T_top with 21 °C:

T_bottom = 21 °C + 29.9 °C

T_bottom = 50.9 °C

Therefore, the temperature at the bottom of the mountain is 50.9 °C.

for such more question on temperature

https://brainly.com/question/14820864

#SPJ8

25% of the students in the seminar are shorter than 65 inches.

To find the percentage of students who are shorter than 65 inches, we first need to find the number of students whose height is less than 65 inches:

There are three students who are shorter than 65 inches: 62, 60, and 58.

Therefore, the percentage of students who are shorter than 65 inches is:

(3 students / 12 students) × 100% = 25%

Note that the value given for 1% × 5 does not appear to be relevant to this question, and is not necessary for the calculation of the percentage of students who are shorter than 65 inches.

For such more questions inches

https://brainly.com/question/876758

#SPJ8

Answer:

17*10= 170

17+10= 27

17-10= 07

17/10= 1.7 or 10/17= 0.5882352941176471

Step-by-step explanation:

Would you multiply the question?     17*10= 170

Would you add the question?       17+10= 27

Would you subtract the question?       17-10= 07

WOuld you divide the question?       17/10= 1.7 or 10/17= 0.5882352941176471

Answer:

x

Step-by-step explanation:

We need to solve this equation by graphing. We need to find what roots will make our equation equal zero. This is the same as drawing a line

\(y = 0\)

and see what points intercepts both graphs.

According to the graph above, one root are between 0 and 0.5 and the other are between 4 and 4.5.

We can find it actual value by solving it

\( - 1 + \frac{9}{2} x - {x}^{2} = 0\)

\( - {x}^{2} + \frac{9}{2} x - 1 = 0\)

Apply Quadratic Formula, we get

\( \frac{9 + \sqrt{65} }{4} \)

and

\( \frac{9 - \sqrt{65} }{4} \)

Which gives us approximately

x=4.27 and 0.23

9514 1404 393

Answer:

  see attached

Step-by-step explanation:

You have a graph of the function ...

  y = 3 +4x -x^2

You want to find solutions to the equation ...

  0 = -1 +9/2x -x^2

This second equation can be made equivalent to ...

  3 +4x -x^2 = p

for some suitable function p.

We can find that function using the relation ...

  (3 +4x -x^2) -p = 0 = -1 +9/2x -x^2

Solving for p, we get ...

  (3 +4x -x^2) -(-1 +9/2x -x^2) = p

  3 +4x -x^2 +1 -9/2x +x^2 = p . . . . . . . eliminate parentheses

  4 -1/2x = p . . . . . . . . . . . . . . . . . . simplify

The line we want is ...

  p = -1/2x +4 . . . . . . . line with y-intercept 4 and slope -1/2

Where this line crosses the graph you have, the x-coordinates are the solutions of the equation -1 +9/2x -x^2 = 0.

The probability of randomly selecting a blue jelly bean from the first bag and then randomly selecting a green jelly bean from the second bag is 1/15 (option a).

Firstly, we need to determine the total number of jelly beans in both bags.

The first bag contains 15 jelly beans (3+5+2+5) and the second bag contains 10 jelly beans (1+7+2).

Therefore, the total number of jelly beans in both bags is 25.

Next, we need to determine the probability of randomly selecting a blue jelly bean from the first bag.

Since there are 5 blue jelly beans out of a total of 15 jelly beans in the first bag, the probability of selecting a blue jelly bean is 5/15 or 1/3.

After selecting a blue jelly bean from the first bag, we move on to the second bag to select a green jelly bean.

Since there are 2 green jelly beans out of a total of 10 jelly beans in the second bag, the probability of selecting a green jelly bean is 2/10 or 1/5.

To determine the probability of both events occurring, we use the multiplication rule of probability.

Therefore, the probability of randomly selecting a blue jelly bean from the first bag and then randomly selecting a green jelly bean from the second bag is (1/3) x (1/5) = 1/15.

Hence, the answer is option (a) 1/15.

To know more about probability here

https://brainly.com/question/11234923

#SPJ1

Answer: \(\frac{2(-\pi^5) }{5} + 18 + C\) , I hope this is right. Im kind of new to integral calculus

Step-by-step explanation:

You essentially want to split this integral into two parts, because its a piecewise function. The conditions on the right side basically say for when x is less than and when x is greater than 0. So, we should split this integral at 0.

The first function says that -pi is less than 0, so change the upper boundary to 0. This make the definite integral bounded at -pi to 0. But now, we have to take the anti derivative of 2x^4 using the reverse power rule. Add one to the power, then divide by the new power. So the new function is \(\frac{2x^5}{5}\) defined at lower boundary -pi and upper boundary of 0. Use the fundamental theorem of calculus to solve the integral. You get \(\frac{2(-\pi ^5)}{5} - \frac{2(0^5)}{5} = \frac{2(-\pi^5) }{5}\). You want to add the 2nd integral to this, so lets go solve that.

Now for this integral, we have the conditions that pi is greater than 0. So 0 will be in the lower boundary this time and pi will be in the upper. Basically apply the same thing from the first integral. Do anti derivative and use fund. theorem of calculus. the anti-derivative of sinx is -cosx. You can take this 9 out because its a constant that is scaling -cosx. So now 9 is on the outside of the integral and you have the definite integral of -cosx with the boundaries of 0 and pi. Plug in pi to get -1, then multiply that by the negative sign to get postive 1. Now let's plug in the lower boundary, 0. Cosine of 0 is 1, then we are multiplying by the negative sign to get -1. Subtract 1 and -1 to get postive 2. Finally multiply that by the 9 from before to get 18

Final Answer finally:

\(\frac{2(-\pi^5) }{5} + 18\)

OH, do not forget the C. This took me 30 minutes of constant typing so hopefully Im right

Answer: H(t) = 43in + (2in/year)*t.

Step-by-step explanation:

At age of 6, the height is 43 inches.

We can define the age of 6 as our t = 0, where t is our variable that represents the number of years after year number 6.

So t = 1 year corresponds to the age of 7 years

t = 2 years corresponds to the age of 8 years, etc.

We know that for the next few years, the child's height will increase by 2 inches per year.

Then at the age of 7, the height will be: 43 in + 2 in

At the age of 8, the height will be: (43in + 2 in) + 2 in = 43in + 2*2in.

And so on, so we can write this as a linear relationship.

H(t) = 43in + (2in/year)*t.

The initial value is the value when t  = 0 years

H(0) = 43in

The initial value is 43 inches.

The growth rate is the coefficient that multiplies the variable, in this case is 2 inches per year or 2 in/year.

The equation that relates x and y is given as y = 2.5x

The relationship between two variables in which one is a constant multiple of the other is referred to as direct variation. For instance, two variables are said to be in proportion when one affects the other. b = ka is the equation if b is directly proportional to a.

The formula for direct variation is in the form of

y = kx

where we have the value of y = 5, the value of x = 2

we have to put this in the formula above

5 = 2k

to get the value of k we would have to divide through by 2

k = 5 / 2

k = 2.5

Hence we would have y = 2.5x

Read more on direct variation here: https://brainly.com/question/6499629

#SPJ1

While an absolute value may be any number, the output from an absolute value expression is always greater than or equal to zero

The absolute value | x | of a real number x is defined as the non-negative value of x without regard to its sign. For example, the absolute value of 3 is 3, and the absolute value of −3 is also 3. The absolute value of a number may be thought of as its distance from zero along real number line.

The absolute value of any number is seen to be always greater than or equal to zero. Both a number and its opposite are the same distance from zero on the number line. Since they have the same distance from zero, they have the same absolute value.

Read more about Absolute Value Function at: https://brainly.com/question/3381225

#SPJ1

Answer:

246/100 as a fraction, and 2 46/100 as a mixed number..

Step-by-step explanation:

Answer: Divide using long division. The whole number portion will be the number of times the denominator of the original fraction divides evenly into the numerator of the original fraction, and the fraction portion of the mixed number will be the remainder of the original fraction division over the denominator of the original fraction.

2 and 23/50

or as a simplified fraction 123/50

Step-by-step explanation:

The probability that their mean weight gain during freshman year is between 0 kg and 3 kg is 70%

It is a branch of mathematics that deals with the occurrence of a random event.

Given,

Amounts of weight that male college students gain during their freshman year are normally distributed

mean of μ = 1.1 kg and

Standard deviation of o= 4.6 kg.

Z score=x-μ/o

=25-1.1/4.6

=23.9/4.6

=5.196

Z score=x-μ/o

=25-1.1/0

=0

Z score=25-1.1/3

=23.9/3

=7.966

By observing the z table the probability that their mean weight gain during freshman year is between 0 kg and 3 kg is 70%

To learn more on probability click:

https://brainly.com/question/11234923

#SPJ1

Answer:

Greatest digit: 8872.

Smallest digit:2278.

9514 1404 393

Answer:

Step-by-step explanation:

Greatest

The greatest possible number is created by putting the greatest allowable digit in the space available that has the highest possible place value. Here, the greatest digit is 8, and the highest place value of a 4-digit number is the thousands place: 8000. Once you have filled that place, you can use the digit 8 one more time in the hundreds place: 8800.

Now, the greatest digit available is the digit 7, and the left-most place you can put it is the tens place: 8870. Finally, the only digit and place available are the digit 2 and the ones place.

Your greatest 4-digit number is 8872.

Smallest

To form the smallest number, you use a similar process, filling places in the number from left to right with the smallest allowable digit. The smallest digit, 2, is allowed twice, so the smallest number that can be formed is 2278.

Answer:

Because 8 hours to drain 80% would mean it takes 10 hours to completely drain the pool leaving the 2 hours to drain.

Step-by-step explanation:

Answer:

Trinomial

Step-by-step explanation:

Its called a Trinomial since it has 3 terms in it                                                                                                                                

Hope its helps!

Answer:

Step-by-step explanation:

Answer: 1

Step-by-step explanation: Do math

Declare a vector of doubles named swimming logs with size of num students. Initialize first element to first student and last element to last student. Fill the middle elements with zeros.

Firstly, declare a vector of doubles named swimming logs with a size of num students. This is done by writing "vector swimming logs(num students);". This creates a vector with the size specified by num students, which can be read from input.

Next, initialize the first element of the vector to first student. This is done by writing "swimming logs[0] = first student;". This sets the first element of the vector to the value of first student, which can be read from input.

Then, initialize the last element of the vector to last student. This is done by writing "swimming logs[num students - 1] = last student;". This sets the last element of the vector to the value of last student, which can be read from input.

Finally, fill the middle elements of the vector with zeros. This is done by writing "for (int i = 1; i < num students - 1; i++) { swimming logs[i] = 0; }". This loop iterates from the second element to the second last element of the vector, setting each element to 0. This completes the initialization of swimming logs with the specified values.

Learn more about vector here

https://brainly.com/question/29740341

#SPJ4

Using the normal distribution, we have that:

a) The sketch of the situation is given at the end of this answer.

b) The probability is:

\(P(2.8 \leq X \leq 7) = 0.8284\)

In a normal distribution with mean and standard deviation , the z-score of a measure X is given by:

\(Z = \frac{X - \mu}{\sigma}\)

In this problem:

Item a:

The part between 2.8 and 7 years is shaded on the sketch given at the end of this answer.

Item b:

The probability is the p-value of Z when X = 7 subtracted by the p-value of Z when X = 2.8, thus:

X = 7:

\(Z = \frac{X - \mu}{\sigma}\)

\(Z = \frac{7 - 4.1}{1.3}\)

\(Z = 2.23\)

\(Z = 2.23\) has a p-value of 0.9871.

X = 2.8:

\(Z = \frac{X - \mu}{\sigma}\)

\(Z = \frac{2.8 - 4.1}{1.3}\)

\(Z = -1\)

\(Z = -1\) has a p-value of 0.1587.

0.9871 - 0.1587 = 0.8284, thus:

\(P(2.8 \leq X \leq 7) = 0.8284\)

A similar problem is given at https://brainly.com/question/25151638

f = k/d^2

Where:

f= force

d= distance

k= constant

f= 23 lb

d = 9

d2 = 3

f2 = x

f = k/d2^2

Replacing:

23 = k / 9^2

23= k/ 81

23*81 = k

k= 1863

When d is 3 in

F = 1863 / 3^2

F= 207 lb

Answer:

57.8 degrees

Step-by-step explanation:

Complementary angles are angles that add up to 90 degrees so you take 32.3 and figure what plus 32.3 equals 90

Yes!, This is a proportional relationship.

A proportional relationship means that the ratios of two variables are equal.

According to the question, the requirements of the recipe are

Number of cups of sour cream required be x1 = 4

Number of packages of onion soup mix required be y1 = 3

Used products by Harlan,

Cups used by Harlan of sour cream be x2 = 2

Packages of onion soup mix used by Harlan be y2 = 1.5

As we can see that,

x1/x2 = y1/y2

4/2 = 3/1.5

2 = 2

L.H.S = R.H.S                          ( ratio is same)

Therefore, we conclude that the above case is a proportional relationship.

To learn more about proportional relationship

visit; https://brainly.com/question/8598338

#SPJ1

The answer is:

Work/explanation:

Bear in mind that the sum of all the angles in a triangle is 180°.

Given two angles, we can easily find the third one.

Let's call it x.

Next, we set up an equation:

\(\sf{54+87+x=180}\)

\(\sf{141+x=180}\)

Subtract 141 on each side.

\(\sf{x=180-141}\)

\(\sf{x=39}\)

Answer:

2 1/3

Step-by-step explanation:

21/9 is 2.33 or 2 1/3

1. The trigonometric ratios are given as follows:

2. The equation to solve for x is given as follows: sin(52º) = x/13.

3. Two equations to solve for m are given as follows:

4. The length of the hypotenuse of the triangle is given as follows: 7.9 inches.

5. The lengths are given as follows:

The three trigonometric ratios are given as follows:

In the second problem, we have that the side x is opposite to the angle of 52º, while the hypotenuse is of 13, hence the equation to solve for x is given as follows:

sin(52º) = x/13.

In item 3, the Pythagorean Theorem is used to solve for m, as follows:

n² + m² = l².

m² = l² - n²

m = square root (l² - n²).

In item 4, we have that the angle opposite to the leg of length 7 inches is of 62º, hence the hypotenuse is given as follows:

sin(62º) = 7/h

h = 7/sin(62º)

h = 7.9 inches.

The length BD in item 5 is obtained as follows:

cos(30º) = BD/5

BD = 5 x cos (30º)

BD = 4.3 cm.

Then the length BC is calculated as follows:

sin(22º) = 4.3/BC

BC = 4.3/sin(22º)

BC = 11.5 cm.

More can be learned about trigonometric ratios at brainly.com/question/24349828

#SPJ1

Answer: 0.4

Have a nice day!

Answer:

0.4 or 2/5

Step-by-step explanation:

You can solve this question by doing \(\frac{1}{5}\) x \(\frac{2}{1}\) to get the answer of \(\frac{2}{5}\) or 0.4.

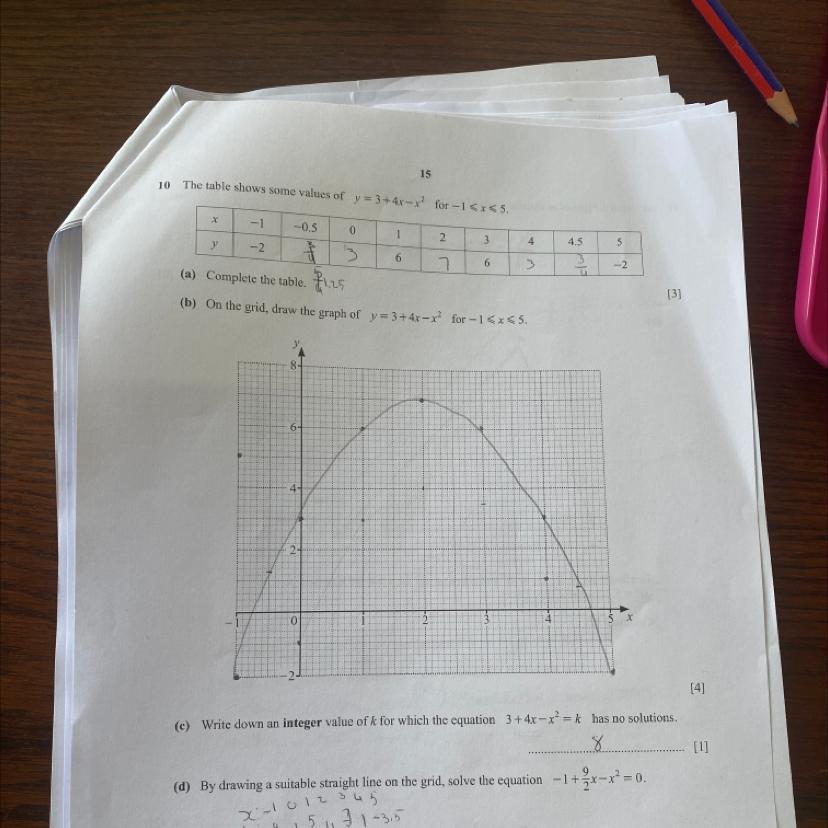
Answer:

Step-by-step explanation:

Answer:

\(+\sqrt{55i}\)

Step-by-step explanation:

Khan <3

Answer:

the area is 30 you have to muiltly the two together

Step-by-step explanation: