Determine the quadrant in which each angle lies -7
Answers
It lies in the quadrant IV.
Since we know that a full circle is broken into four parts known as quadrants into regions of π/2.Since quadrant 1 ranges from 0 to π/2, quadrant 2 ranges from π/2 to π, then quadrant 3 ranges from π to 3π/2, and at last quadrant 4 ranges from 3π/2 to 2π.
And we know 2π is equal to approx 6.28 radians, so each quadrant will have 2π/ 4 = π2 ≈1.57 radians
So for angle -7 it will be = −7/(π/2) ≈−4.45.
So moving around the circle, it appears halfway through the quadrant IV.
To know more about the quadrant refer to the link https://brainly.com/question/7196312?referrer=searchResults.
#SPJ9
Related Questions
A rational number
can be a fraction that is not a whole number.
must be positive.
cannot be a whole number.
is always an integer.
Answers
Answer:
A
Step-by-step explanation:
On anotherv question these two guys said A, I got it right, and ye.
Answer:
answer is A
can be a fraction that is not a whole number
Step-by-step explanation:
hope this helps!
Find: P(Small and Blue)
Remember to reduce your answer.
Large | Small
Red | 17 | 3
Blue | 8 | 12
HURRY!!

Answers
Red to tiny will have a probability of 12/20.
Describe probability.
In other terms, probability is a number that indicates the likelihood of an event occurring. Probability is defined as the ratio of favorable outcomes to all outcomes.
Probability is calculated as follows: N = N samples / N favorable outcomes
There are 20 blue numbers, of which the large ones are 17 and the small ones 3. Likewise, there are 20 red digits; the large ones are 8 and the small ones are 12.
The likelihood of receiving a little red number will be determined as follows:
Probability is calculated as follows: N = N samples / N favorable outcomes
12 good outcomes total.
There are 20 samples total.
Fill out the formula above with the value.
12/20 is the probability.
As a result, 12/20 will be the likelihood of red to little.
Learn more about probability by reading on.
brainly.com/question/24756209
#SPJ1
Consider the isosceles triangle below where the side lengths are given in cm:
Part A: Is the side length √ 24 + 4 rational or irrational? Explain your reasoning.
Part B: The expression 2(√24+4)+√6 can be used to find the perimeter of the triangle. What does the "2" represent in this expression?
Part C: Write the perimeter of the triangle in simplest form. Show your work. (Remember to use units)

Answers
Answer:
I think is B
because its the one that sounds good
1. For each of the following sets, tell whether it is a group or is not a group. If it is a group, provide an explanation. If it is not a group, show which group axiom(s) it does not satisfy. (a) The nonnegative integers under addition (b) The positive rational numbers under multiplication
2. List the elements in (Z*₁₁)² = {x² mod 11 : x ∈ Z*₁₁} and (Z*₁₃) = {x² mod 13 : x ∈ Z*₁₃}
Answers
1. (a) The nonnegative integers under addition form a group.
This is because they satisfy the four group axioms:
- Closure: Adding two nonnegative integers always results in a nonnegative integer.
- Associativity: Addition of integers is associative, meaning that for any three nonnegative integers a, b, and c, (a + b) + c = a + (b + c).
- Identity element: The number 0 is the identity element, as adding it to any nonnegative integer leaves the integer unchanged.
- Inverse element: For every nonnegative integer a, the additive inverse -a exists in the set of nonnegative integers. Adding a and -a results in the identity element 0.
(b) The positive rational numbers under multiplication do not form a group. This is because they do not satisfy the inverse element axiom. Specifically, not every positive rational number has a multiplicative inverse that is also a positive rational number. For example, the number 2 does not have a multiplicative inverse in the set of positive rational numbers.
2. (Z*₁₁)² = {0, 1, 4, 9, 5, 3, 3, 5, 9, 4, 1}
(Z*₁₃) = {0, 1, 4, 9, 3, 12, 10, 10, 12, 3, 9, 4, 1}
To know more about integers visit:
brainly.com/question/28457183
#SPJ11
help please!!!!!!!!!

Answers
Let u = (1,0, -1), v = (4,3,-2), and w = (2, 3, -2). Find the orthogonal projection of w into the plane spanned by the vectors u and v. Show that the matrix A is orthogonal if and only if its transpose A⁻ is orthogonal.
Answers
The transpose of A⁻¹ is the inverse of the transpose of A⁻¹, which implies that if A⁻¹ is orthogonal, then A is orthogonal. Therefore, we have shown that the matrix A is orthogonal if and only if its transpose A⁻¹ is orthogonal.
To find the orthogonal projection of vector w into the plane spanned by vectors u and v, we need to calculate the projection vector proj_w(uv).
First, we calculate the normal vector n of the plane. The normal vector is obtained by taking the cross product of vectors u and v:
n = u x v
= (1, 0, -1) x (4, 3, -2)
The cross product can be calculated as follows:
n = ((0)(-2) - (-1)(3), (-1)(4) - (1)(-2), (1)(3) - (0)(4))
= (-3, -6, 3)
Next, we normalize the normal vector n to obtain the unit normal vector n:
n = n / ||n||
= (-3, -6, 3) / √(9 + 36 + 9)
= (-3, -6, 3) / √54
= (-1/√6, -2/√6, 1/√6)
Now, we can calculate the projection of vector w onto the plane using the formula:
proj_w(uv) = w - ((w · n) / (n · n)) * n
The dot product of w and n is given by:
w · n = (2)(-1/√6) + (3)(-2/√6) + (-2)(1/√6)
= -2/√6 - 6/√6 - 2/√6
= -10/√6
The dot product of n and n is:
n · n = (-1/√6)(-1/√6) + (-2/√6)(-2/√6) + (1/√6)(1/√6)
= 1/6 + 4/6 + 1/6
= 6/6
= 1
Substituting these values into the projection formula, we have:
proj_w(uv) = (2, 3, -2) - ((-10/√6) / 1) * (-1/√6, -2/√6, 1/√6)
= (2, 3, -2) + (10/√6)(-1/√6, -2/√6, 1/√6)
= (2, 3, -2) + (-10/6, -20/6, 10/6)
= (2, 3, -2) + (-5/3, -10/3, 5/3)
= (2 - 5/3, 3 - 10/3, -2 + 5/3)
= (1/3, 1/3, -1/3)
Therefore, the orthogonal projection of vector w into the plane spanned by vectors u and v is (1/3, 1/3, -1/3).
Now, let's prove the statement that the matrix A is orthogonal if and only if its transpose A⁻¹ is orthogonal.
To prove this, we need to show two conditions:
If A is orthogonal, then A⁻¹ is orthogonal:
If A is orthogonal, it means that A · A⁻¹ = I, where I is the identity matrix.
Taking the transpose of both sides, we have (A · A⁻¹)ᵀ = Iᵀ, which simplifies to (A⁻¹)ᵀ · Aᵀ = I.
This shows that the transpose of A⁻¹ is the inverse of the transpose of A, which implies that if A is orthogonal, then A⁻¹ is orthogonal.
If A⁻¹ is orthogonal, then A is orthogonal:
If A⁻¹ is orthogonal, it means that (A⁻¹) · (A⁻¹)ᵀ = I, where I is the identity matrix.
Taking the transpose of both sides, we have ((A⁻¹) · (A⁻¹)ᵀ)ᵀ = Iᵀ, which simplifies to ((A⁻¹)ᵀ) · (A⁻¹) = I.
Learn more about transpose at: brainly.com/question/32293193
#SPJ11
the probability that a car has a certain factory defect is 825. the probability that a car has a certain factory defect and needs an oil change is 750. what is the probability that a car needs an oil change given that it has a certain factory defect?give your answer as a fraction in simplest form.
Answers
The result is 5/6, which is the probability expressed as a fraction in simplest form.
To find the probability that a car needs an oil change given that it has a certain factory defect, we divide the probability of having both the defect and needing an oil change by the probability of having the defect alone.
Let's denote:
P(D) is the probability of having the defect (given as 0.825).
P(O|D) is the probability of needing an oil change given that the car has the defect (given as 0.750).The probability that a car needs an oil change given that it has the defect can be calculated as:
P(O|D) / P(D)
Substituting the given values:
0.750 / 0.825
To simplify the fraction, we can divide both the numerator and denominator by their greatest common divisor, which is 75:
(750/75) / (825/75) = 10/11.
Therefore, the probability that a car needs an oil change given that it has a certain factory defect is 5/6, expressed as a fraction in simplest form.
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
factoring trinomials 4x^2-15x-25
Answers
Answer:
For a polynomial of the form ax2+bx+c a x 2 + b x + c , rewrite the middle term as a sum of two terms whose product is a⋅c=4⋅−25=−100 a ⋅ c = 4 ⋅ - 25 ...
Step-by-step explanation:
suppose you decided to write down all whole numbers from 1 to 99,999. how many times would have have to write the number 1?
Answers
The digit "1" appears 99,920 times when writing down all whole numbers from 1 to 99,999. To determine this, we can consider each place value separately.
1. Units place (1-9): The digit "1" appears once in each number from 1 to 9.
2. Tens place (10-99): In this range, the digit "1" appears in all numbers from 10 to 19 (10 times) and in the tens place of numbers 21, 31, ..., 91 (9 times). So the digit "1" appears 10 + 9 = 19 times in the tens place.
3. Hundreds place (100-999): The digit "1" appears in all numbers from 100 to 199 (100 times) in the hundreds place. Similarly, it appears in the hundreds place of numbers 201, 202, ..., 299 (100 times), and so on up to 901, 902, ..., 999 (100 times). So in the hundreds place, the digit "1" appears 100 * 9 = 900 times.
4. Thousands place (1000-9999): Similar to the previous cases, the digit "1" appears in the thousands place 1000 times in the range from 1000 to 1999. Also, it appears 1000 times in the thousands place of numbers 2000 to 2999, and so on up to 9000 to 9999. So in the thousands place, the digit "1" appears 1000 * 9 = 9000 times.
5. Ten thousands place (10,000-99,999): The digit "1" appears in the ten thousands place 90000 times since it occurs in all numbers from 10000 to 99999.
Adding up the counts from each place value:
1 + 19 + 900 + 9000 + 90000 = 99920
Therefore, the digit "1" appears 99,920 times when writing down all whole numbers from 1 to 99,999.
Learn more about digit here: https://brainly.com/question/14961670
#SPJ11
F(x) + 4x^5 - X^4 + 26x^2 -14x + 3 possible rational zeros
Answers
To determine the possible rational zeros of the function f(x) = 4x^5 - x^4 + 26x^2 - 14x + 3, we can apply the Rational Root Theorem.
The possible rational zeros are all the divisors of the constant term (3) divided by the divisors of the leading coefficient (4). Therefore, the possible rational zeros are ±1, ±3, and ±1/2.
The Rational Root Theorem states that if a polynomial equation has a rational root (p/q), where p is a factor of the constant term and q is a factor of the leading coefficient, then p/q is a possible root of the equation.
In this case, the constant term is 3, and the leading coefficient is 4. The factors of 3 are ±1 and ±3, while the factors of 4 are ±1 and ±2. By applying the Rational Root Theorem, the possible rational zeros of the function are all the possible combinations of the factors: ±1, ±3, ±1/2.
Therefore, the possible rational zeros of the function f(x) = 4x^5 - x^4 + 26x^2 - 14x + 3 are ±1, ±3, and ±1/2. These values can be tested to see if any of them are actual zeros of the function by substituting them into the equation and checking if the result is equal to zero.
To learn more about coefficient click here:
brainly.com/question/1594145
#SPJ11
A population follows a logistic DDS given by Pn+1 = 1.205pn -0.00019p²n
a) Determine the growth rate
r = Round to three decimal places. b) Determine the carrying capacity. Carrying capacity =
c) State the equilibrium values for this population. Smaller pe = Round to the nearest integer value. Larger pe = Round to the nearest integer value.
Answers
a) The growth rate (r) for the logistic difference equation P(n+1) = 1.205P(n) - 0.00019P(n)² b) The carrying capacity represents the maximum population size that the environment can sustain. c) P(n+1) = P(n) = P(e), where P(e) represents the equilibrium population
a) To determine the growth rate (r), we examine the coefficient of the linear term in the logistic difference equation. In this case, the coefficient is 1.205. Therefore, the growth rate is approximately 1.205.
b) The carrying capacity (K) represents the maximum population size that the environment can sustain. In the logistic difference equation, the carrying capacity can be found by taking the limit as n approaches infinity. In this equation, the carrying capacity is not explicitly given. However, in a logistic model, the carrying capacity often corresponds to the value of P(n) when the equation reaches equilibrium. Therefore, to find the carrying capacity, we need to find the equilibrium values of the population.
c) To find the equilibrium values of the population, we set P(n+1) = P(n) = P(e), where P(e) represents the equilibrium population. Solving the equation 1.205P(e) - 0.00019P(e)² = P(e), we obtain two equilibrium values: a smaller equilibrium (P(es)) and a larger equilibrium (P(el)). These equilibrium values can be rounded to the nearest integer.
Learn more about linear term here:
https://brainly.com/question/14368568
#SPJ11
In a bag there are blue discs, green discs and white discs.
There are eight times as many blue discs as green discs.
number of blue discs : number of white discs = 6:5
One disc is selected at random.
Work out the probability that the disc is either blue or white.
Answers
The probability that the disc is either blue or white is 11/59
Working out the probability that the disc is either blue or white.Given that
number of blue discs : number of white discs = 6:5
number of blue discs : number of green discs = 1:8
So, we have
Blue : White = 6 : 5
Blue : Green = 1 : 8
This can be expressed as
Blue : Green = 6 : 48
So, we have
Blue : White : Green = 6 : 5 : 48
So, we have
Blue or White : Green = 11 : 48
So, the probability is
P = 11/(48 + 11)
Evaluate
P = 11/59
Read more about probability at
https://brainly.com/question/24756209
#SPJ1
Can you help me with this plz

Answers
Answer:
A Q1
cos 59° = x/16
x = 16 cos 59°
x = 8.24
Q2
BC is given 23 mi
Maybe AB is needed
AB = √34² + 23² = 41 (rounded)
Q3
BC² = AB² - AC²
BC = √(37² - 12²) = 35
Q4
Let the angle is x
cos x = 19/20
x = arccos (19/20)
x = 18.2° (rounded)
Q5
See attached
Added point D and segments AD and DC to help with calculation
BC² = BD² + DC² = (AB + AD)² + DC²
Find the length of added red segments
AD = AC cos 65° = 14 cos 65° = 5.9
DC = AC sin 65° = 14 sin 65° = 12.7
Now we can find the value of BC
BC² = (19 + 5.9)² + 12.7²
BC = √781.3
BC = 28.0 yd
All calculations are rounded
Find the volume formed by rotating the region enclosed by: \[ x=4 y \text { and } y^{3}=x \text { with } y \geq 0 \] about the \( y \)-axis. Volume =
Answers
To calculate the volume formed by rotating the region enclosed by the equations \(x = 4y\) and \(y^3 = x\) (with \(y \geq 0\)) about the \(y\)-axis, we can use the method of cylindrical shells. By integrating the volume element of a cylindrical shell over the appropriate interval, we can determine the total volume.
To calculate the volume, we consider the cylindrical shells formed by rotating vertical strips of the region around the \(y\)-axis. The height of each shell is given by \(dy\), and the radius of each shell is the corresponding value of \(x\). Since \(x = 4y\) and \(y^3 = x\), we can express the radius of each shell as \(r = 4y\) and the height as \(h = y\). The volume element of a cylindrical shell is \(dV = 2\pi rh \, dy = 8\pi y^2 \, dy\). Integrating this expression over the interval \([0, 1]\) (based on the range of \(y\)) gives us the total volume. The integral becomes \(\int_{0}^{1} 8\pi y^2 \, dy\), which can be evaluated to find the volume.
To know more about cylindrical shells here: brainly.com/question/33182921
#SPJ11
b
Score: 7/21 7/21 answered Question 11 A baseball player has a batting average of 0.165. What is the probability that he has exactly 1 hits in his next 7 at bats? The probability is Submit Question B1p
Answers
The probability that a baseball player has exactly 1 hit in his next 7 at bats is 0.371, assuming his batting average is 0.165.
Let's find the probability using the binomial probability formula:P(x) = C(n, x) * p^x * (1-p)^(n-x)where:
P(x) = probability of getting x successes
n = total number of trials
x = number of successful trials
p = probability of success in a single trial
q = probability of failure in a single trial, which is equal to 1-p
Summary:
The probability of a baseball player having exactly 1 hit in the next 7 at-bats is 0.371, assuming his batting average is 0.165. This was calculated using the binomial probability formula, which takes into account the probability of success in a single trial, the number of trials, and the number of successful trials desired.
Learn more about probability click here:
https://brainly.com/question/13604758
#SPJ11
help please!!!!!!!!!!!!!!!

Answers
Answer:
C
Step-by-step explanation:
.........................
pyramid a is a dilation with scale factor 2 of pyramid b. how many times greater is the volume of pyramid a than the volume of pyramid b?
Answers
The volume of pyramid A is 8 times greater than the volume of pyramid B.
The volume of a pyramid is calculated by taking the area of its base and multiplying it by the height and then dividing it by 3. In this case, pyramid a is a dilation with a scale factor of 2 of pyramid b, meaning that all of its dimensions will be doubled. This means that when calculating the volume of pyramid a, the base and height will be twice as large, so the volume of the pyramid a will be 8 times greater than the volume of pyramid b. This can be expressed mathematically as V_a = 8V_b. This is because the scale factor is multiplied by both the base and the height of the pyramid, resulting in an increase by a factor of 8 (2 x 2 x 2). The base and height are the two components that make up the pyramid's volume, so when they are both multiplied by the same scale factor, the volume of the pyramid increases by the same factor. In this case, the scale factor is 2, so the volume increases by a factor of 8.
To know more about pyramid refer to the link brainly.com/question/29464385
#SPJ4
Solve for x in the equation x2 + 4x-4- 8.
0 x = -6 or x = 2
X=-2+2-2
O x = -2 or x = 6
X=2+2112
Answers
Answer:
2(n+2x-6)
Step-by-step explanation:
n x 2+4x-4-8
Which function represents the graph below?

Answers
Answer:
b
Step-by-step explanation:
Since it intercepts y at 4, and x at 2, we use y=ax+b and rearrange to get the equation from y=2x+4 to 2x-y=-4
Answer:
b) 2x - y = -4
Step-by-step explanation:
The y-intercept is the y-coordinate of the point (0, b) where the graph crosses the y-axis. It is also the value of y when x = 0.
The crosses the y-axis at point (0, 4). Therefore, the y-intercept, b = 4.
Next, we need to determine which of the given options matches the graph. It helps to transform each of them into their slope-intercept form, y = mx +b:
a) 2x + y = 42x - 2x + y = - 2x + 4
y = -2x + 4 (This is not the correct answer because the slope, m = -2. The given graph has a positive slope).
b) 2x - y = - 42x - 2x - y = - 2x - 4
-y = -2x - 4
Divide both sides by -1:
\(\frac{-y}{-1} = \frac{-2x - 4}{-1}\)
y = 2x + 4 This is the correct answer because it matches the y-intercept (0, 4), and has a positive slope of 2.
We could easily disregard the last two options because both of their y-intercept is 0.
Therefore, the correct answer is Option b) 2x - y = - 4
-5b+6=4-5b help me please someone it is due at the end of classs
Answers
Answer:
24
Step-by-step explanation:
Answer:
6 = 4
No Solution
Step-by-step explanation:
The water company has a different monthly pricing plan for residential customers than for business customers. For each pricing plan, cost in dollars) dependson water used in hundreds of cubic feet, HCF), as shown below.(a) If the monthly water usage is 18 HCF, which plan costs less?Residential Plan/Business PlanHow much less does it cost than the other plan?(b) For what amount of monthly water usage do the plans cost the same?If the monthly water usage is more than this amount, which plan costs less?

Answers
In order to answer the question, we need to refer to the image provided with the two different plans:
Question a) In order to decide which plan costs less for 18 HCF , we go on the horizontal axis to the mark 18 and read tha values for the red line(Residential) versus the blue line (Business)
We read $36 for the residential and $32 for the business, so the business costs less than the residential , and the difference is 4 dollars.
Question b) The plans cost the same at the point where the two lines intersect. That is for HCF = 14 and which shows $28 dollars.
Then, if the monthly water usage is MORE (that means we move to the right of that intersection point for larger values of the horizontal variable HCF), then the RED line becomes on top of the blue one, meaning that the cost in dollars for the red line will be LARGER that the blue one. The answer for this part is therefore that: If the monthly uses goes above this 14 HCF, the business plan costs less.

24 cent is _ percent of 80 cents
Answers
Answer:
24 cent is 30 percent of 80 cents
Step-by-step explanation:
24: 80*100 =
(24*100): 80 =
2400: 80 = 30
Answer:
30%
step by step explanation is given above.

Determine the coordinates of Q(6, −4) after a reflection in the line x=2
Answers
The coordinates of (6, -4) after a reflection in the line x = 2 are:
(-4, -4)
What are the coordinates after the reflection?If we have a point (x, y) and we do a reflection in the line x = a, the new coordinates of the point will be:
(a - x, y)
In this case, we have (6, -4) and the line of reflection is x = 2, then the coordinates after the reflection are:
(2 - 6, -4) = (-4, -4)
Learn more about reflections:
https://brainly.com/question/4289712
#SPJ1
Identify the length of JK.
ASAP please

Answers
Answer:
15x+5
Step-by-step explanation:
(7x+5)+(8x)
A rectangular playing field is 70 yards long. Its area is 3,150 yards what is the width of the feild
Answers
Answer:
45 yards
Step-by-step explanation:
Formula to find area of rectangle: Length * Width
Given:
Length = 70 yards
Area = 3,150 yards
Width = 3,150/70
==> 45 yards
Width = 45 yards
What is the equation? (the last option you can't see isn't an option)
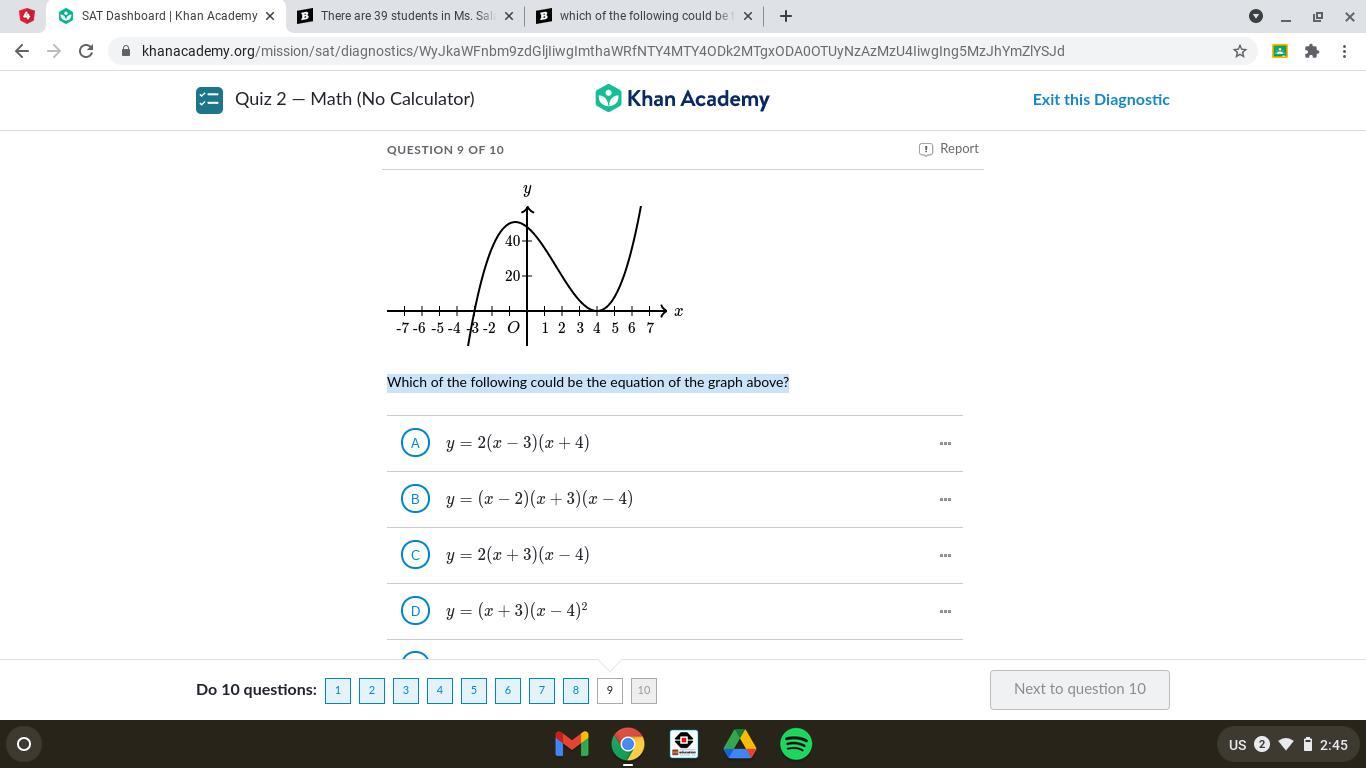
Answers
Step-by-step explanation:
\(y = (x + 3) {(x - 4)}^{2} \)
What is JL brainliest for answer

Answers
Answer:
JL = 12.5
Step-by-step explanation:
\( In\: \triangle JKL, KM\perp JL\)
Therefore, by geometric mean property:
\( KM^2 = JM\times ML\)
\( 6^2 = 8\times ML\)
\( 36 = 8\times ML\)
\( \frac{36}{8} = ML\)
\(ML= 4.5 \)
JL = JM +ML
JL = 8 + 4.5
JL = 12.5
21. A street vendor buys watches from a
is manufacturer for $28 each. The vendor marks up
the price by 175% What is the retail price of a
watch after the mark up is applied?
Answers
What integer is equivalent to 3^-2
Answers
Answer:
1/9
Step-by-step explanation:
\( {3}^{ - 2} \)
\( \frac{1}{3 \times 3} \)
\( \frac{1}{9} \)
Consider the equations below for the lengths of line segments AB and AM, where M is the midpoint of line segment AB.
AB= 8x-6
AM = 3x+1
What is the length of line segment AB?
AB=
Answers
Answer: uihnjnijnjjnjuuuuuu890999999999
Step-by-step explanation: 977789gbj