determine the minimum sample size required when you want to be be
90%
confident that the sample mean is within one unit of the population mean and
σ=12.2.
Assume the population is normally distributed.
Answers
To determine the minimum sample size required when you want to be 90% confident that the sample mean is within one unit of the population mean, we can use the formula:
n = [Z*(σ/√n)]^2
where n is the sample size, Z is the Z-score corresponding to the confidence level (90% in this case), σ is the population standard deviation, and √n is the square root of the sample size.
Substituting the given values, we get:
n = [1.645*(12.2/√n)]^2
Simplifying this equation, we get:
n = 22.99
Since we can't have a fractional number of people in a sample, we round up the result to get:
n = 23
Therefore, a sample size of at least 23 is required to be 90% confident that the sample mean is within one unit of the population mean when σ=12.2 and assuming a normal distribution of the population.
For more questions like population visit the link bellow:
https://brainly.com/question/15402443
#SPJ11
Related Questions
How do you write 6x (to the 3rd power) -60x (to the 2nd power) +144x in factored form?
Answers
Answer:
6x(x-4)(x-6)Step-by-step explanation:
I assume your expression is:
6x^3-60x^2+144x.
I'll use that information.
Factor 6x^3−60x^2+144x
6x^3−60x^2+144x
=6x(x−4)(x−6)
What is the surface area of this design?
5 in.
8in
8 in.
4 in.
4 in.
Answers
Answer:
Step-by-step explanation:
245
Answer:
Step-by-step explanation:

If the graph of f(x)=x2, how will the graph be affected if it is changed to f(x)=3x2?
Answers
There will be a vertical stretch with a factor of 3.

PLEASE HELP!!!!!!!!
What is the value of x
3x+14+5x-2=10x-18
Thank you sooooo much have a blessed day
Answers
have a wonderful day =)
Each side of a square is (x-5) units. Which expression can be used to represent the area of the square
Answers
Answer:
4x-20
Step-by-step explanation:
(x-5) + (x-5) + (x-5) + (x-5) = 4x-20
or
(4)(x-5) = 4x-20
The expression x² - 10x + 25 will represent the a square with side (x-5) units.
What is a square?A square is a geometrical figure in which we have four sides each side must be equal and the angle between two adjacent sides must be 90 degrees.
Area of square = Side²
The perimeter of square = 4× side
Length of diagonal of square = √(2) × side
Given,
Side of square = (x - 5)
The area of a square is given by = Side²
So,
Area = (x - 5)²
Area = x² - 10x + 25
Hence,The expression x² - 10x + 25 will represent the a square with side (x-5) units.
For more about a square,
https://brainly.com/question/2189895
#SPJ2
5. lan is 5 years older than Craig. If the sum of their ages is 45, find both
their ages. Be sure to create an equation then solve. *
Answers
Answer: Ian is 25 and craig is 20
Step-by-step explanation:
(45 - 5) /2 +5 to one of them
Answer:
Craig is 20 and Ian is 25 years old.
Step-by-step explanation:
I = Ian
C = Craig
I = C + 5
45 = C + I
45 = C + C + 5
45 - 5 = C + C
40 = 2C
C = 20
I = 20 + 5
Craig is 20 and Ian is 25.
Drag the tiles to the correct boxes to complete the pairs. Not all tiles will be used. Match the pairs of figures that have the same volume. 3-D shape of a cone is represented. The cone has a radius of 4 units and a height of 12 units. 3-D shape of a rectangular prism is represented. The rectangular prism has a length of 18 units, a width of 6 units, a height of 6 units. 3-D shape of a rectangular prism is represented. The rectangular prism length is labeled 16 units, width of 6 units, and height of 6 units. 3-D shape of a cylinder is represented. The cylinder has a radius of 3 units and a height of 8 units. 3-D shape of a cone is represented. The cone has a radius of 8 units and a height of 9 units. 3-D shape of a rectangular prism is represented. The rectangular prism length is labeled 8 units, width of 8 units, height of 9 units. arrowBoth 3-D shape of a cylinder is represented. The cylinder has a radius of 4 units and a height of 12 units. arrowBoth 3-D shape of a cone is represented. The cone has a radius of 6 units and a height of 6 units. arrowBoth Reset Next © 2023 Edmentum. All rights reserved.
Answers
The pair of figures having same volume are:
a. The cylinder has a radius of 3 units and a height of 8 units ; The cone has a radius of 6 units and a height of 6 units.
b. The cone has a radius of 8 units and a height of 9 units ; The cylinder has a radius of 4 units and a height of 12 units.
c. The rectangular prism length is labeled 16 units, width of 6 units, and height of 6 units ; The rectangular prism length is labeled 8 units, width of 8 units, height of 9 units.
What is volume of a figure?
Volume is a unit of measurement for three-dimensional space. It is usually stated quantitatively in terms of a number of imperial or US-standard units as well as SI-derived units.
i. The cone has a radius of 4 units and a height of 12 units.
⇒ Volume = π\(r^{2} \frac{h}{3}\)
⇒ Volume = π\(4^{2} \frac{12}{3}\)
⇒ Volume = 64 π
⇒ Volume = 201 cubic units
ii. The rectangular prism has a length of 18 units, a width of 6 units, a height of 6 units.
⇒ Volume = length * width * height
⇒ Volume = 18 * 6 * 6
⇒ Volume = 648 cubic units
iii. The rectangular prism length is labeled 16 units, width of 6 units, and height of 6 units.
⇒ Volume = length * width * height
⇒ Volume = 16 * 6 * 6
⇒ Volume = 576 cubic units
iv. The cylinder has a radius of 3 units and a height of 8 units.
⇒ Volume = π\(r^{2}\)h
⇒ Volume = π\(3^{2}\) * 8
⇒ Volume = 72 π
⇒ Volume = 226 cubic units
v. The cone has a radius of 8 units and a height of 9 units.
⇒ Volume = π\(r^{2} \frac{h}{3}\)
⇒ Volume = π\(8^{2} \frac{9}{3}\)
⇒ Volume = 192 π
⇒ Volume = 603 cubic units
vi. The rectangular prism length is labeled 8 units, width of 8 units, height of 9 units.
⇒ Volume = length * width * height
⇒ Volume = 8 * 8 * 9
⇒ Volume = 576 cubic units
vii. The cylinder has a radius of 4 units and a height of 12 units.
⇒ Volume = π\(r^{2}\)h
⇒ Volume = π\(4^{2}\) * 12
⇒ Volume = 192 π
⇒ Volume = 603 cubic units
viii. The cone has a radius of 6 units and a height of 6 units.
⇒ Volume = π\(r^{2} \frac{h}{3}\)
⇒ Volume = π\(6^{2} \frac{6}{3}\)
⇒ Volume = 72 π
⇒ Volume = 226 cubic units
Hence, three pairs have the same volume.
Learn more about volume from the given link
https://brainly.com/question/463363
#SPJ1
The missing figures have been attached below.



5. Carrie Burnside is single, earns $350. 15 weekly, and claims 1 allowance.
6. Ray Barbee, a radio announcer, is single, earns $300. 74 weekly, and
claims 2 allowances.
7. Stephen Jensen, a pharmacist, is married, earns $369. 23 weekly, and
claims 2 allowances.
8. Lisa Steamer is married, earns $290. 34 weekly as a receptionist, and
claims no allowances.
9. Catherine Hall, a restaurant hostess, earns $208. 35 a week. She is single
and claims 2 allowances.
10. Veterinarian Ike Stone earns $925. 32 a week. He is single and claims
1 allowance.
11. Doug Smalley, a meteorologist, is married and earns $1,304. 30 a week.
He claims 2 allowances.
12. Kristen Martinez, a dentist, is married, earns $1,352. 75 a week, and
claims 1 allowance.
Answers
Carrie will have $15,481.24 after taxes for a year assuming she works 52 weeks.
First, let's calculate the total taxes she pays each week:
Federal income tax rate = 10% of $350.15 = $35.02
State income tax rate = 5% of $350.15 = $17.51
Total taxes per week = $35.02 + $17.51 = $52.53
Now, we can calculate the total amount of taxes she pays for a year:
Total taxes for a year = $52.53 x 52 weeks = $2,731.56
Amount Carrie will have after taxes for a year:
Annual income before taxes = $350.15 x 52 weeks = $18,212.80
Net income after taxes = Annual income before taxes - Total taxes for a year
Net income after taxes = $18,212.80 - $2,731.56 = $15,481.24
To know more about federal income tax rate, here
brainly.com/question/11886585
#SPJ4
--The complete Question is, Carrie Burnside is single, earns $350.15 weekly, and claims 1 allowance. If the federal income tax rate is 10% plus an additional 5% state income tax rate, how much will Carrie have after taxes for a year assuming she works 52 weeks? --
Which one?
-Quadratic
-linear
-Exponential

Answers
The first table is a quadratic function, while the second table is an exponential function
How to determine the function type of the tables?Table 1
On this table, we can see that:
As x increases by 1, the value of y do not change constantly
This means that the table is a non-linear function
The y values on the table are
-5 -4 -1 4 11
Calculate the first difference
So, we have
-5 -4 -1 4 11
1 3 5 7
Calculate the second difference
So, we have
-5 -4 -1 4 11
1 3 5 7
2 2 2
Since the second differences are equal, then the table is a quadratic table
Table 2
On this table, we can see that:
As x increases by 1, the value of y do not change constantly
This means that the table is a non-linear function
However, we can see that the y values have a common rate of 2
This means that the table is an exponential table
Read more about non-linear functions at
https://brainly.com/question/12240424
#SPJ1
help with this question

Answers
Answer:
A
Step-by-step explanation:
x= -2
Consider a male restroom design with minimum plumbing requirements of 12 water closets and 13 lavatories, which one of the following is closest to the minimum space required with considering urinal substitution? Select one: O a. 222 b. 219 c. 237 d. 249
Answers
none of the provided options (a, b, c, d) appear to be accurate or close to the minimum space required.
To determine the minimum space required for a male restroom design with the given plumbing requirements, we need to consider the minimum space required for water closets and lavatories.
The minimum space required for water closets is typically around 30-36 inches per unit, and for lavatories, it is around 24-30 inches per unit.
Since the design requires a minimum of 12 water closets and 13 lavatories, we can estimate the minimum space required as follows:
Minimum space required for water closets = 12 water closets * 30 inches = 360 inches
Minimum space required for lavatories = 13 lavatories * 24 inches = 312 inches
Adding these two values together, we get a total minimum space requirement of 672 inches.
Among the given options, the closest value to 672 inches is option d) 249. However, this value seems significantly lower than the expected minimum space requirement.
To know more about minimum visit:
brainly.com/question/21426575
#SPJ11
I need numbers 9 and 10 on please ok, i dont understand it
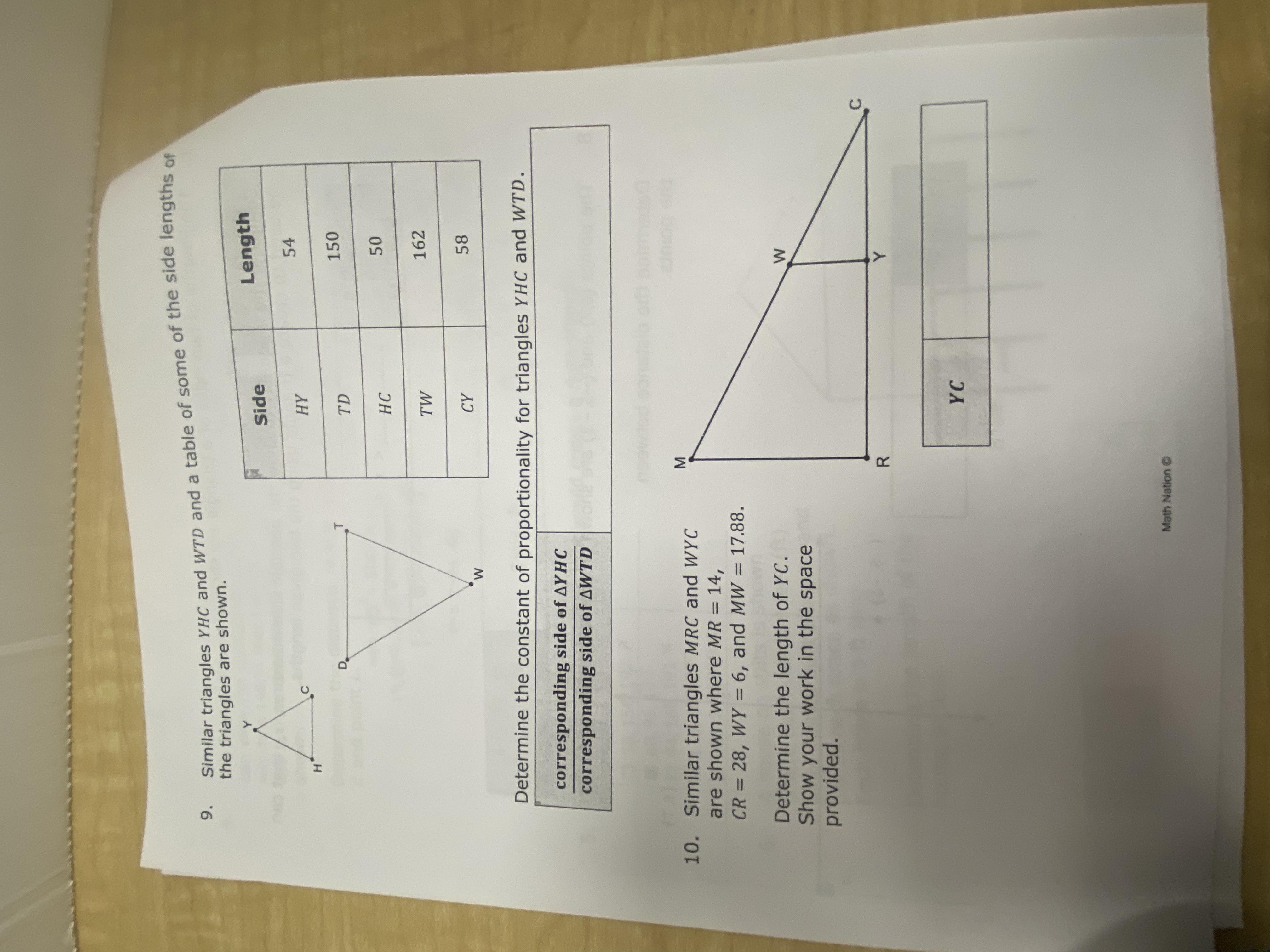
Answers
9)
The constant of proportionality is 3.
10)
The measure of YC is 12.
We have,
9)
YHC and WTD are similar triangles.
This means,
The ratio of the corresponding sides is equal.
Now,
TD/HC = TW/HY
Substituting the values,
150/50 = 162/54
3 = 3
This means,
3 is the constant of proportionality.
And,
10)
MRC and WYC are similar triangles.
This means,
The ratio of the corresponding sides are equal.
MR/WY = CR/YC
14/6 = 28/YC
YC = 28/14 x 6
YC = 4/2 X 6
YC = 4 x 3
YC = 12
Thus,
The constant of proportionality is 3.
The measure of YC is 12.
Learn more about triangles here:
https://brainly.com/question/25950519
#SPJ1
In computing a seasonal index, specific seasonals were tabulated for each month. The averages over time for the twelve months were obtained and summed. If the mean seasonal factor for June was 96.9, and the sum for all twelve months is 1195, the adjusted seasonal index for June is
Answers
If the mean seasonal factor for June was 96.9, and the sum for all twelve months is 1195, the adjusted seasonal index for June is 8.11
To calculate the adjusted seasonal index for June, we need to divide the mean seasonal factor for June by the sum of the seasonal factors for all twelve months and then multiply the result by 100.
Adjusted seasonal index for June = (Mean seasonal factor for June / Sum of seasonal factors for all twelve months) × 100
Adjusted seasonal index for June = (96.9 / 1195) × 100 ≈ 8.11
The adjusted seasonal index for June is approximately 8.11.
More on mean: https://brainly.com/question/259493
#SPJ11
(a) Construct a relative frequency histogram of the data. Comment on the shape of the distribution. Choose the carrect graph below. A. B. C. D. 4kelstrve I req. What is the shape of the distribution?
Answers
A relative frequency histogram was constructed for the given data, and it was observed that the distribution is skewed to the right.
A relative frequency histogram provides a visual representation of the distribution of a dataset by displaying the relative frequencies of observations in each interval or bin.
In this case, the data is not normally distributed, as most of the observations are concentrated towards the lower end of the range and there are a few high values that skew the distribution to the right.
This can be observed by noticing that the histogram bars are taller on the left side and shorter on the right side, with a long tail towards the higher values.
Therefore, it can be concluded that the distribution is skewed to the right. This type of distribution is also known as a positively skewed distribution.
Learn more about the relative frequency histogram from the given link:
https://brainly.com/question/30331733
#SPJ11
The table shows the distance between Greenville and nearby towns. The distance between Astaville and
Greenville is 14 miles less than the distance between Greenville and Jonesborough,
Distance between Greenville and
Nearby Towns(miles)
Jonesborough
24
Willfower 21
Maybem 30
Part 1 out of 2
Enter two equations that state the relationship of the distances between the three towns. Use x as the
variable

Answers
Someone please help me!!!!

Answers
Answer:
Below.
Step-by-step explanation:
Left side = 2 cos^2 ( π/4 - A/2) - 1
= 2 ( cos π/4 cos A/2 + sin π/4 sin A/2)^2 - 1
Now sin π/4 and cos π/4 = 1 /√2 so:
= 2 ( 1/√2 cos A/2 + 1/√2 sin A/2)^2 - 1
= 2 * 1/2( cos^2 A/2 + sin^2 A/2 + 2 sin A/2 cos A/2) - 1
But cos^2 a/2 + sin^2 A/2 = 1 so we have:
2 * 1/2( 1 + 2sin A/2 cos A/2) - 1
= 1 + 2 sin A/2 cos A/2 - 1
= 2 sin A/2 cos A/2
Using the identity 2 sin A cos A = sin 2A
2 sin A/2 cos A/2 = sin A = right side.
So left side = right side and the identity is proved.
Answer: see proof below
Step-by-step explanation:
Use the Double Angle Identity: cos 2A = 2cos²A - 1
Use the Difference Identity: cos (A - B) = cosA · cosB + sinA · sinB
Use the Unit Circle to evaluate: cos (π/2) = 0 & sin (π/2) = 1
Proof LHS → RHS
\(\text{Given:}\qquad \qquad \qquad \qquad 2\cos^2\bigg(\dfrac{\pi}{4}-\dfrac{A}{2}\bigg)-1\\\\\\\text{Double Angle Identity:}\quad \cos2\bigg(\dfrac{\pi}{4}-\dfrac{A}{2}\bigg)\\\\\\\text{Simplify:}\qquad \qquad \qquad \quad \cos\bigg(\dfrac{\pi}{2}-A\bigg)\\\\\\\text{Difference Identity:}\qquad \cos\dfrac{\pi}{2}\cdot \cos A+\sin \dfrac{\pi}{2}\cdot \sin A\\\\\\\text{Unit Circle:}\qquad \qquad \qquad 0\cdot \cos A+1\cdot \sin A\\\\\\\text{Simplify:}\qquad \qquad \qquad \qquad \sin A\)
LHS = RHS: sin A = sin A \(\checkmark\)

whats 78,563 divided by 98
Ty for whoever helps me <3
Answers
Answer:
801.66
Step-by-step explanation:
calculator
Answer:
801.6632653061
Step-by-step explanation:
.......
51
Select the correct answer.
If a six-sided die is rolled 30 times, how many times can you expect to get a 6?
OA. 3
OB. 5
C. 6
D. 10
Reset
Next
Answers
Answer:
Step-by-step explanation:
There are 6 possibilities for each roll: 1, 2, 3, 4, 5 and 6. Each of these has a probability of 1/6.
If you roll the die 30 times, the probability of getting a 6 would be 30 x (1/6) = 5. The answer is 5.
Answer:There are 6 numbers on a die.
The probability of rolling a 6 would be 1/6 for each time you roll the die.
Multiply the number of rolls by 1/6.
30 rolls x 1/6 probability = 5 times.
Step-by-step explanation:
Partial Derivative Applications, Vectors and Matrices
If z = F(u, v, w) where u = r 2 , v = −2s 2 , and w = lnr + lns,
find ∂z/∂r and ∂z/∂s.
Answers
The values of ∂z/∂r and ∂z/∂s. These partial derivatives will depend on the specific function F(u, v, w) provided.
To find ∂z/∂r and ∂z/∂s, we need to differentiate z = F(u, v, w) with respect to r and s.
Given that u = r^2, v = -2s^2, and w = ln(r) + ln(s), we can substitute these values into z = F(u, v, w).
So, z = F(r^2, -2s^2, ln(r) + ln(s)).
To find ∂z/∂r, we differentiate z with respect to r while treating s as a constant. This gives us:
∂z/∂r = ∂F/∂u * ∂u/∂r + ∂F/∂w * ∂w/∂r.
Similarly, to find ∂z/∂s, we differentiate z with respect to s while treating r as a constant. This gives us:
∂z/∂s = ∂F/∂v * ∂v/∂s + ∂F/∂w * ∂w/∂s.
Since we don't have the specific function F(u, v, w) mentioned in the question, we cannot determine the values of ∂z/∂r and ∂z/∂s. These partial derivatives will depend on the specific function F(u, v, w) provided.
To know more about partial derivatives, visit:
https://brainly.com/question/28751547
#SPJ11
Hallar la desviación estándar de los siguientes datos: 5,5; 7,8; 6,4; 8,2; 6,4; 5,7; 7,8; 6,4; 8,2
Answers
Answer:
what?
Step-by-step explanation:
ind the amount in the account after $800 is invested for 1 year at 9ompounded monthly. (enter a number. round your answer to two decimal places.)
Answers
the amount in the account after $800 is invested for 1 year at 9% compounded monthly would be $875.03 (rounded to two decimal places).
Assuming an annual interest rate of 9% compounded monthly, the amount in the account after one year can be calculated using the formula:
A = P(1 + r/n)^(nt)
where:
A = the amount in the account after one year
P = the principal amount (initial investment) = $800
r = the annual interest rate (as a decimal) = 0.09
n = the number of times the interest is compounded per year = 12 (for monthly compounding)
t = the time period in years = 1
Plugging in these values, we get:
A = 800(1 + 0.09/12)^(12*1)
A = 800(1.0075)^12
A = 800(1.0938)
A = 875.03
Therefore, the amount in the account after $800 is invested for 1 year at 9% compounded monthly would be $875.03 (rounded to two decimal places).
Visit to know more about Decimal:-
https://brainly.com/question/28393353
#SPJ11
assume that y varies inversely with x. if y = 8 when x = 1.55, find x when y = -0.62
Answers
Answer:
y varies inversely with x is written as
y = k /x
where k is the constant of variation
y = 8 x = 1.55
8 = k / 1.55
Multiply through by 1.55
k = 12.4
The formula is
y = 12.4 / x
when y = - 0.62
- 0.62 = 12.4/x
- 0.62x = 12.4
Divide both sides by - 0.62
x = 12.4/-0.62
x = - 20
When y = - 0.62 x = - 20
Hope this helps
In an isosceles triangle, one side is 6 more than 3 times a number and the congruent side is 10 less than
5 times the same number, what is that number?
a.2
b.8
c.16
d. none of above
Answers
need help due today .
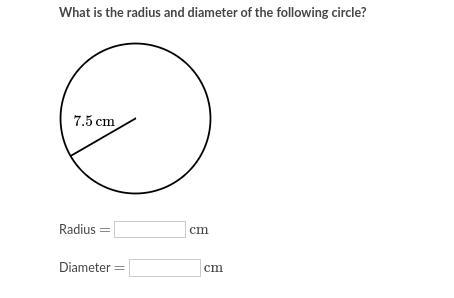
Answers
Answer:
Radius=7.5cm
Diameter=15cm
Step-by-step explanation:
The radius is half of the diameter which is the length of the circle measured across (or through I guess), so the radius is what is shown 7.5, and the radius doubled (x2) is the diameter so 7.5x2 = 15.
HOPE THAT HELPS AND MAKES SENSE! :)
The rate of change of the volume V with respect to time t of water leaking from a tank is proportional to the cube of the volume. Which of the following is a differential equation that could describe this relationship? a. dV/dt = -1.4t^3 b. dV/de = -0.2V^3 c. dV/dt = 0.75t^3 d. dV/dt = 0.15V^3
Answers
d. dV/dt = -0.15V³ is a differential equation that could describe the relationship between the rate of change of the volume V with respect to time t of water leaking from a tank, and the cube of the volume.
Differential Equation for LeakA differential equation is an equation that relates a function and its derivatives. In this case, the function is the volume V of water in the tank, and the variable is time t. The problem states that the rate of change of the volume V with respect to time t is proportional to the cube of the volume. This means that the rate at which the volume is changing is directly proportional to the cube of the volume, and the proportionality constant is a negative number.
The differential equation that describes this relationship is dV/dt = -0.15V³, where dV/dt represents the rate of change of the volume with respect to time, and -0.15V³ represents the proportionality constant times the cube of the volume. The negative sign indicates that the volume is decreasing over time, as water is leaking out of the tank. This differential equation can be used to model the behavior of the water leaking from the tank, and can be used to determine the volume of water remaining in the tank at any given time.
Learn more about Differential Equation for Leak here:
https://brainly.com/question/27476892
#SPJ4
suppose the mean income of firms in the industry for a year is 80 million dollars with a standard deviation of 13 million dollars. if incomes for the industry are distributed normally, what is the probability that a randomly selected firm will earn less than 96 million dollars? round your answer to four decimal places.
Answers
The probability that a randomly selected firm will earn less than 96 million dollars is 0.8907
The given data is that the mean income of firms in the industry for a year is 80 million dollars with a standard deviation of 13 million dollars. Now, it is required to find the probability that a randomly selected firm will earn less than 96 million dollars if incomes for the industry are distributed normally.
The probability is calculated by the Z-score formula which is given as below:
z = (x - μ) / σ
Where,μ = 80 (Mean), x = 96 (Randomly selected firm income), σ = 13 (Standard deviation)
Putting the values in the formula we have,
z = (96 - 80) / 13z = 1.23
Now we will use the Z-table to find the probability value. From the Z-table, we can say that the probability of Z-score = 1.23 is 0.8907.
Therefore, the probability that a randomly selected firm will earn less than 96 million dollars is 0.8907 (approx) when rounded off to four decimal places.
To learn more about probability refer :
https://brainly.com/question/31078740
#SPJ11
3x+1=38 solve and check please
Answers
Hello!
The first step is to subtract 1 from both sides.
\(\bf{3x+1=38}\)
\(\bf{3x=37}\)
Now, divide both sides by 3:
\(\bf{\displaystyle\frac{37}{3} }\)
Can this fraction be simplified? Nope.
Why? Because 37 and 3 do not have any common factors, except 1 (and what's the point of dividing by 1?)
Hence, the answer is
\(\huge\boxed{\text{Answer:{\boxed{\circ\star{\frac{37}{3} }}}}}\)
Hope everything is clear.
Let me know if you have any questions!
#KeepOnLearning
\(\boxed{An~Emotional~Helper!}\)
Use trigonometric identities, algebraic methods, and inverse trigonometric functions, as necessary, to solve the following trigonometric equation on the interval [0, 28t).Round your answer to four decimal places, if necessary. If there is no solution, indicate "No Solution."- 15csc?(x) - 1 = -32cot(x)yea

Answers
To solve the equation:
\(-15\csc ^2x-1=-32\cot x\)We meed to remember the identity:
\(\csc ^2x=\cot ^2x+1\)Plugging this identity in the equation we have:
\(\begin{gathered} -15(\cot ^2x+1)-1=-32\cot x \\ -15\cot ^2x-15-1=-32\cot x \\ 15\cot ^2x-32\cot x+16=0 \end{gathered}\)Hence we have the quadratic equation in the cotangent:
\(15\cot ^2x-32\cot x+16=0\)To solve it let:
\(w=\cot x\)Then we have the quadratic equation:
\(15w^2-32w+16=0\)let's use the general formula to solve it:
\(\begin{gathered} w=\frac{-(-32)\pm\sqrt[]{(-32)^2-4(15)(16)}}{2(15)} \\ =\frac{32\pm\sqrt[]{1024-960}}{30} \\ =\frac{32\pm\sqrt[]{64}}{30} \\ =\frac{32\pm8}{30} \\ \text{then} \\ w=\frac{32+8}{30}=\frac{40}{30}=\frac{4}{3} \\ \text{ or } \\ w=\frac{32-8}{30}=\frac{24}{30}=\frac{4}{5} \end{gathered}\)Once we know the value of w we can find the value of x, remember the definition of w, then we have:
\(\begin{gathered} \cot x=\frac{4}{3} \\ \text{ and} \\ \cot x=\frac{4}{5} \end{gathered}\)Since it is easier to work with the tangent function we will use the fact that:
\(\tan x=\frac{1}{\cot x}\)Hence our equations take the form:
\(\begin{gathered} \tan x=\frac{3}{4} \\ \text{and} \\ \tan x=\frac{5}{4} \end{gathered}\)Finally to solve the equations we need to remember that the tangent function has a period of pi, therefore we have that:
\(\begin{gathered} x=\tan ^{-1}(\frac{3}{4})+\pi n \\ \text{and} \\ x=\tan ^{-1}(\frac{5}{4})+\pi n \end{gathered}\)where n is any integer number. To find the solutions in the interval given we plug n=0 and n=1 in each expression for x; therefore, the solutions in the interval are:
\(\begin{gathered} x=0.6435 \\ x=0.8961 \\ x=3.7851 \\ x=4.0376 \end{gathered}\)Determine whether the following statement is true or false. If the statement is false, make the necessary change(s) to produce a true statement.
{x∣x∈N and 25
Answers
Statement: {x ∣ x ∈ N and 25 < x < 30} ⊆ {x ∣ x ∈ N and 10 < x ≤ 29} is a true statement.
{x ∣ x ∈ N and 25 < x < 30} ⊆ {x ∣ x ∈ N and 10 < x < 30}.
We have to check whether this statement is true or false and to modify it, if it is not correct.
We know that N represents a set of natural numbers and this set is countable.
{x ∣ x ∈ N and 25 < x < 30} represents the set of natural numbers that are between 25 and 30.
These elements are 26, 27, 28 and 29. {x ∣ x ∈ N and 10 < x < 30} represents the set of natural numbers that are between 10 and 30.
These elements are 11, 12, 13, …, 28 and 29.
If we compare the two sets, we see that the first set is a subset of the second set.
Therefore, we can conclude that the given statement is true.
To learn more on natural numbers :
https://brainly.com/question/2228445
#SPJ11
What is the value of the following function when x = 0?
y=-5
y=-2
Y=-1
Y= 0
Answers
The numeric value of the function when x = 0 is found replacing each instance of x by zero in the definition of the function.
If a graph is given, then the numeric value is given as the value of y when the function crosses the y-axis.
How to find the numeric value of a function or of an expression?To find the numeric value of a function or of an expression, we replace each instance of the variable in the function or in the expression by the value at which we want to find the numeric value.
Supposing we have a function definition, then the numeric value at x = 0 is found replacing each instance of x by zero.
On graph, x = 0 is when the graph of the function touches or crosses the y-axis.
Missing InformationThe problem is incomplete, hence the general procedure to obtain the numeric value at x = 0 was presented.
Learn more about the numeric values of a function at brainly.com/question/28367050
#SPJ1