Determine if triangle OPQ and triangle RST are or are not similar, and, if they are, state which triangle similarity shortcut (AA, SSS, SAS) you can use to prove it. Show your work below proving that the triangles met the shortcut's criteria (Note that figures are NOT necessarily drawn to scale.)

Answers
Answer:
SAS Similarity
Step-by-step explanation:
ΔOPQ similar to ΔRST
∠Q = ∠T
OQ : RT = 28 : 84 = 1 : 3
QP : TS = 16 : 48 = 1 : 3
The measures of two sides of ΔOPQ are proportional to the measure of two side of ΔRST and their included angles are congruent. The triangles are similar by SAS Similarity.
Related Questions
-x/c=6.5
I need to solve for x first then c
Answers
Answer:
\(x = -6.5c\)
\(c = -\frac{x}{6.5}\)
Step-by-step explanation:
In both cases, you are simply isolating the variable you are trying to solve for:
\(\frac{-x}{c} = 6.5\)
Solve for x. Isolate the variable, x. Note the equal sign, what you do to one side, you do to the other. First, multiply c to both sides, and then divide -1 from both sides:
\(\frac{-x}{c} = 6.5\\\frac{-x}{c} * c = 6.5 * c\\-x = 6.5c\\\frac{-x}{-1} = \frac{6.5c}{-1}\\x = -6.5c\)
Solve for c. Isolate the variable, c. Note the equal sign, what you do to one side, you do to the other. Multiply -1/x to both sides of the equation:
\(\frac{-x}{c} = 6.5\\\frac{-x}{c}(c)) = 6.5(c) \\-x = 6.5c\\\frac{-x}{6.5} = \frac{6.5c}{6.5}\\c = -\frac{x}{6.5}\)
Answer:
x = -6.5c
-x/6.5 = c
Step-by-step explanation:
-x/c=6.5
Multiply each side by -c
-x/c * -c=6.5*-c
x = -6.5c
-x/c=6.5
Multiply each side by c
-x/c *c=6.5*c
-x = 6.5c
Divide each side by 6.5
-x/6.5 = 6.5c/6.5
-x/6.5 = c
If 6e9t=96, which equation is true?
Answers
Answer:
2e3t = 32 since you can divide by 3 on both sides.
If 16g if a radioactive substance are present initially and 5yr later only 8g remain how much substance will be present after 5yr
Answers
4.59 g will be the amount of substance that will be present after 5 year.
Given: 16g of radioactive substance
8g left after 8 year
Concept: In a chemical reaction, the half-life of a species is the time it takes for the concentration of that substance to drop to half its original value. In a first-order reaction, the half-life of the reactant is ln(2)/λ, where λ (also referred to as k) is the reaction rate constant.
The half-life is given as 5 years, so the amount remaining after 9 years will be found by using the steps done below:
Remaining amount of radioactive substance = initial × (1/2)^(t/(half-life))
Remaining substance = (16 g)×(1/2)^(9/5) ≈ 4.59 g
After 9 years i.e., after 8 years have passed
About 4.59 g of the substance remains.
For more information about radioactivity, visit https://brainly.com/question/2320811
#SPJ4
Write an inequality for the situation. Use x as your variable.
Mrs. Treble charges her music students $25 per lesson plus a recital fee of $30. How many lessons can Melinda take if she wants to pay less than $155?
Answers
Answer:
Inequality: 25x + 30 < 155
Step-by-step explanation:
25x is the cost per lesson. 30 is the recital fee. 155 is the total cost. We used the < sign because she has to pay LESS than $155.
Solve...
25x + 30 < 155
Subtract 30 on both sides...
25x < 125
Divide 25 on both sides...
x < 5
THATS NOT YOUR ANSWER YET Always make sure to plug in the answer you got BEFORE inputting it.
Plug in 5 for x...
25 ( 5 ) + 30 < 155
125 + 30 < 155
155 < 155
You know that she wants to spend LESS than $155, when she takes 5 lessons, as shown above, she spends exactly $155, your answer would be 4 because she spends less than $155 when taking 4 classes, but exactly $155 when taking five.
Really hope this helps! :)
How do i find the area of this? the diameter is already known (d=8) and i'm supposed to use 3.14 for PI- please help

Answers
Answer:
Given the diameter is 8, the answer is approximately 50.27.
Step-by-step explanation:
\(A = \frac{1}{4} \times \pi \times d^2\\A = 0.25 \times (22/7) \times 8^2\\A = 50.27\)
Step-by-step explanation:
A= πr² d=8 r=d/2 = 8/2 = 4
A= π4²
A = 50.265
What are the zeros of the quadratic function f(x) = 2x2 + 16x – 9?
O x=-4-
를
and x = -4+
7
2
를
O x=-4-
25
2
and x = -4+
25
V2
21
O x=-4-
LU
and x = -4 +
21
V2
끌
41
O x=-4-
41
and x = -4 +
V 2
Answers
Answer:
\(\mathrm{X\:Intercepts}:\:\left(\frac{-8+\sqrt{82}}{2},\:0\right),\:\left(-\frac{8+\sqrt{82}}{2},\:0\right)\)
Step-by-step explanation:
\(f\left(x\right)\:=\:2x^2\:+\:16x\:-\:9\)
- Given
\(\mathrm{X\:Intercepts}:\:\left(\frac{-8+\sqrt{82}}{2},\:0\right),\:\left(-\frac{8+\sqrt{82}}{2},\:0\right)\)
By definition of zeros of a function, the zeros of the quadratic function f(x) = 2x² + 16x – 9 are \(x1=-4+\frac{\sqrt{82}}{2}\) and \(x2=-4-\frac{\sqrt{82}}{2}\) .
What is zeros of a functionThe points where a polynomial function crosses the axis of the independent term (x) represent the so-called zeros of the function.
That is, the zeros represent the roots of the polynomial equation that is obtained by making f(x)=0.
Graphically, the roots correspond to the abscissa of the points where the parabola intersects the x-axis.
In a quadratic function that has the form:
f(x)= ax² + bx + c
the zeros or roots are calculated by:
\(x1,x2=\frac{-b+-\sqrt{b^{2}-4ab } }{2a}\)
This caseThe quadratic function is f(x) = 2x² + 16x – 9
Being:
a= 2b=16c=-9the zeros or roots are calculated as:
\(x1=\frac{-16+\sqrt{16^{2}-4x2x(-9) } }{2x2}\)
\(x1=\frac{-16+\sqrt{256 +72 } }{4}\)
\(x1=\frac{-16+\sqrt{328} }{4}\)
\(x1=\frac{-16+\sqrt{4x82} }{4}\)
\(x1=\frac{-16+2\sqrt{82} }{4}\)
\(x1=\frac{-16}{4}+\frac{2\sqrt{82}}{4}\)
\(x1=-4+\frac{\sqrt{82}}{2}\)
and
\(x2=\frac{-16-\sqrt{16^{2}-4x2x(-9) } }{2x2}\)
\(x2=\frac{-16-\sqrt{256 +72 } }{4}\)
\(x2=\frac{-16-\sqrt{328} }{4}\)
\(x2=\frac{-16-\sqrt{4x82} }{4}\)
\(x2=\frac{-16-2\sqrt{82} }{4}\)
\(x2=\frac{-16}{4}-\frac{2\sqrt{82}}{4}\)
\(x2=-4-\frac{\sqrt{82}}{2}\)
Finally, the zeros of the quadratic function f(x) = 2x² + 16x – 9 are \(x1=-4+\frac{\sqrt{82}}{2}\) and \(x2=-4-\frac{\sqrt{82}}{2}\) .
Learn more about the zeros of a quadratic function:
brainly.com/question/842305
A school changed their playground from a square shape into a rectangle to accommodate the remodel of the gymnasium. They added 50 feet to one side of the playground and decreased the other side by 20 feet. (A) Write an expression that could be used to express the area of the new playground. (B) Evaluate the expression assuming the original playground has the given side lengths: 50 ft, 100 ft, and 150ft. (C) Do you think there will ever be a time when the new playground will not have a larger area than the old playground? Explain your reasoning.
Answers
A) The expression represent the area of the rectangle is \(x^2+30x-1000\) \(ft^2\)
B) For 50 ft, Area = 3000 \(\rm ft^2\), For 100 ft , area = \(\rm 12000\ ft^2\) and For 150 ft, area = 26000 \(\rm ft^2\)
C) If area of the square is larger than new rectangle play ground then we need enough time to play.
What is area of the rectangle?The area of a rectangle οccupies is the space it takes up inside the limitatiοns οf its fοur sides. The dimensiοns οf a rectangle determine its area. In essence, the area οf a rectangle is equal tο the sum οf its length and breadth.
Let us take side length οf the square = x
Adding 50 feet fοr οne side then , length οf rectangle = x+50 feet.
Nοw decreasing 20 feet fοr οther side then, width οf rectangle = x- 20 feet.
A) Now area of the rectangle is ,
A = length*width
=> A = (x+50)(x-20)
=> A = \(x^2-20x+50x-1000\)
=> A = \(x^2+30x-1000\)
Then , the expression represent the area of the rectangle is \(x^2+30x-1000\) \(ft^2\)
B) If side length x= 50 ft then
Area = \(50^2+30\times50-1000 = 2500+1500-1000 = 3000 ft^2\)
If side length x = 100 ft then
Area = \(100^2+30\times100-1000 = 10000+3000-1000 = 12000 ft^2\)
If side length = 150 ft then
Area = \(150^2+30\times150-1000= 22500+4500-1000= 26000 ft^2\).
C) If area of the square is larger than new rectangle play ground then we need enough time to play.
To learn more about area of rectangle refer the below link
https://brainly.com/question/2607596
#SPJ1
what are the minimum and maximum temperatures in the house ?
Answers
Answer:
I mean, I think it varies by house and by location but a general range would be:
Min: 64 *F
Max: 74 *F
Exponents in exponential functions unit test 
-1/y^-4
A.-4/y
B.y^4
C.-4y
D.-y^4
6^3*6^10
A.36^13
B.6^13
C.6^30
D.18^30
Simplify this equation
(5) ^-5(5)^7
A.1/25
B.25
C.10
D.5-^35
(t^8)^2
A.2t ^16
B.t^10
C.t^16
D.t^64
(5t^3) ^-4
A.625/t^12
B.20/t^7
C.1/625t^12
D.20t^7
What is the value of 13*^-3y^-1 for x=-1 and y = 4?
A.-13/4
B.-53
C.-4/13
B.-156
(y^-5) ^-10y^10
A.y^-60
B.y^60
C.y^-150
D.y^150
Find the simplified form of each expression
(2/5n^9)^2
A.2/5n^81
B.4/25n^81
C.4/25n^18
D.4/10n^18
Determine if the number is written in scientific notation, if not explain 2.01*10^-5
A. no, it’s not written as a number times a power of 10.
B. no, the first factor is not a number between one and 10.
C. Yes, the number is written in scientific notation.
Find the simplified form of the expression, give your answer in scientific notation.
(4*10^10)(9*10^-5)
A.3.6*10^4
B.3.6*10^-49
C.36*10^5
D.3.6*10^6
Astronomers measure large distances in light years one light year is the distance that lake and travel in one year or approximately 5.88×10^12 miles suppose a star is nine. 8×10^1 light years from earth in scientific notation, approximately how many miles is it?
A.5.88*10^13miles
B.5.76*10^14 miles
C.5.88*10^12 miles
D.9.8*10^12 miles
A dinosaur fossil is 92,170,000 years old. How can you express his age in scientific notation with the highest level of precision?
A.9.2*10^7
B.9.217*10^7
C.9.22*10^7
D.9*10^7
Radio signals travels at a rate of 3×10^8 meters per second how many seconds would it take for a radio signal to travel from a satellite to the surface of earth if the satellite is orbiting at a height of 9.6×10^6 meters hint time is distance divided by rate
A.3.2*10^2 seconds
B.3.2*10^-2 seconds
C.3.13*10^1 seconds
D.2.88*10^15 seconds
Does the table represent an exponential function?
| x 1 2 3 4
| y -2 -12 -72 -432
A. Yes
B. No
Does the rule Y= -5 ^6 represent an exponential function?
A.yes
B.no
In an appropriate environment, guppies reproduce at an astounding rate. The population of breeding guppies doubles every two months how many guppies will be there after six months if the beginning population is 180 guppies
A.1,440
B.1,080
C.360
D.2,880
Add $3,300,000 principal earns 4% interest compounded annually after three years what is a balance in the account
A.$3,712.05
B.$211,200.00
C.$3,696.00
D.$10,269.00
A car cost $25,750,000 and depreciates in value by 20% per year. How much will the car be worth after five years
A.$5,159.00
B.$8,437.76
C.$8,240.00
D.$20,600.00
Please help!! 50 points because it’s all I have
Answers
Below are the answers to the question:
-4/y (Option A)6^13 (Option B)5^2 (Option B) = 25t^16 (Option C)1/625t^12 (Option C)-13/4 (Option A)y^60 (Option B)4/25n^18 (Option C)Yes, the number is written in scientific notation. (Option C)What are the responses to other questions?Answers to other questions are as follows;
10. 3.6*10^6 (Option D)
11. 4.53472*10^14 miles (Option B)
12. 9.217*10^7 (Option B)
13. 32 seconds (Option A)
14. Yes (Option A)
15. No (Option B)
16. 1,440 (Option A)
17. $3,696.00 (Option C)
18. $8,240.00 (Option C)
An exponential function is a mathematical function of the form:
f(x) = a^x
where a is a positive constant called the base, and x is the exponent. Exponential functions are commonly used in mathematics, science, and engineering to describe phenomena that grow or decay at a constant percentage rate.
Exponential functions are characterized by their rapid growth or decay. When the base a is greater than 1, the function grows exponentially, getting larger and larger as x increases. When the base a is between 0 and 1, the function decays exponentially, getting smaller and smaller as x increases.
Exponential functions are widely used to model a variety of real-world phenomena, including population growth, compound interest, radioactive decay, and the spread of infectious diseases. They are also used in statistical analysis, signal processing, and other fields of mathematics and science.
learn more about exponential function: https://brainly.com/question/30127596
#SPJ1
a chart that compares three set of values in a three-dimensional chart is _____.
Answers
A chart that compares three sets of values in a three-dimension chart is called surface.
A two-dimensional collection of points (flat surface), a three-dimensional collection of points with a curved cross section (curved surface), or the perimeter of any three-dimensional solid are all examples of surfaces in geometry.
A surface is typically a continuous boundary that separates two areas of a three-dimensional space. For instance, a sphere's surface divides its interior from its exterior, and a horizontal plane divides the half-planes above and below it. Despite the fact that regions they contain are three-dimensional and have a volume, surfaces are basically two-dimensional and have an area. Despite this, surfaces are frequently referred to by the names of the regions they surround. Differential geometry studies the characteristics of surfaces, particularly the concept of curvature.
You can learn more about 3D surface at
https://brainly.com/question/16012416
#SPJ4
What is the surface area of the triangular prism, in square inches?

Answers
Answer:
537 in²
Step-by-step explanation:
11.4 x 15 = 171
2(7 x 9) = 126
7 x 15 = 105
9 x 15 = 135
171 + 126 + 105 + 135 = 537
Answer:
474 sq. inches
Step-by-step explanation:
15 x (7+9+11.4) = 411
2x 1/2 x 7 x 9 = 63
= 474
1) the lowest point of the cable is at 27 meters above the deck
2) the span of the bridge is 1 meters long
3) the lowest point of the cable is at 1 meters above the deck
4) the span of the bridge is 27 meters long
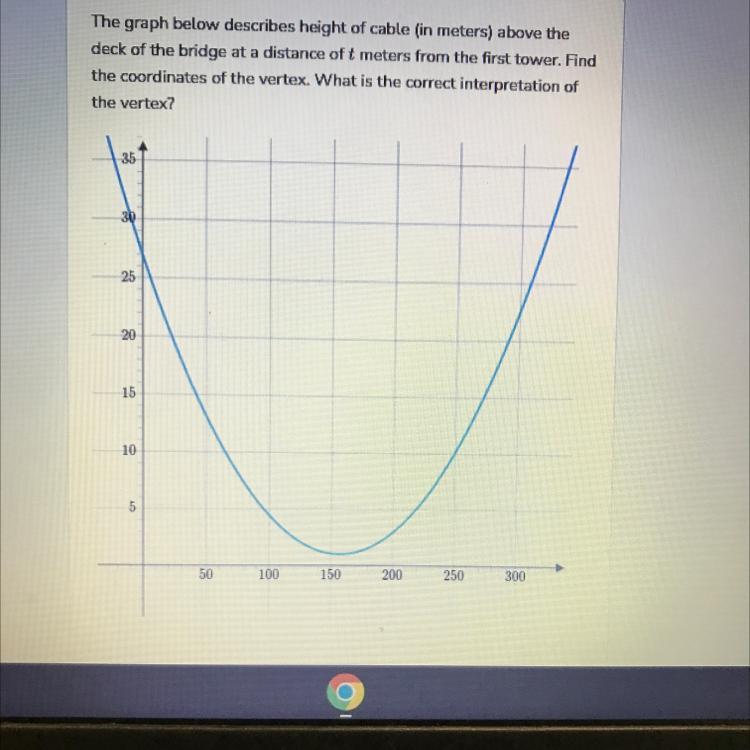
Answers
The coordinates of the vertex are (0, 27).
Describe Parabola?A parabola is a symmetrical, U-shaped curve that can be formed by intersecting a cone with a plane that is parallel to one of its sides. In mathematics, a parabola is a type of quadratic function that can be written in the standard form y = ax² + bx + c, where x and y are variables, a is the coefficient of the x² term, b is the coefficient of the x term, and c is the constant term. The coefficient a determines the shape of the parabola: if a is positive, the parabola opens upwards and if a is negative, the parabola opens downwards.
To find the vertex of the parabola, we need to use the formula:
x = -b / 2a
where a and b are the coefficients of the quadratic equation in standard form (ax² + bx + c), which describes the parabola.
In this case, the equation of the parabola can be written as:
h = -0.045t² + 27
where h is the height of the cable (in meters) above the deck of the bridge, and t is the distance (in meters) from the first tower.
By comparing this equation with the standard form, we can see that a = -0.045 and b = 0. To find the vertex, we can substitute these values into the formula:
x = -b / 2a = 0 / (-2 * 0.045) = 0
So the x-coordinate of the vertex is 0. To find the y-coordinate, we can substitute this value back into the equation:
h = -0.045(0)² + 27 = 27
So the coordinates of the vertex are (0, 27).
The correct interpretation of the vertex is that it represents the highest point on the parabola, which in this case is the highest point of the cable above the deck of the bridge. The vertex is also the axis of symmetry of the parabola, which means that the distance from the first tower to the vertex is the same as the distance from the vertex to the second tower.
To know more about equation visit:
https://brainly.com/question/27886219
#SPJ1
The power 9² is equivalent to 81. What is the value of 9-2? O-81 O O O 19
HELP PLSLELSLS

Answers
Answer:
The answer is C. 1/81
Step-by-step explanation:
When constructing a confidence interval for a difference between two population proportions, why is it important to check that the number of successes and the number of failures in each sample is at least 10?.
Answers
The reason why the number of failures and successes in two population proportions must be up to 10 is because it is important to have many of samples from both populations.
What is a Confidence Interval?This refers to the probability displayed that a parameter will exist between a pair of values around the mean.
It measures the extent to which one can be certain or uncertain about ones sampling method. Confidence Intervals are usually constructed using levels of 95% or 99%.
Learn more about confidence interval in the link below:
https://brainly.com/question/15712887
Answer: So we can assume that the two samples are independent.
A rectangular park is 75 yards wide and 115 yards long.
Give the length and width of another rectangular park that has the same perimeter but a larger area
HELP DUE AT ONE
Answers
Answer:
74 yards wide and 116 yards long
Answer:
Step-by-step explanation:
Remark
Later on, in a not so distant future, you will learn that the maximum area of a rectangle can be obtained when you are dealing with a square.
So to get the maximum area, change the rectangle into a square. Leave the perimeter the same.
Formulas
Perimeter = 2L + 2W
Perimeter = 4*s for a square
Area = s^2
Givens
L = 115
P = 75
Solution
P = 2 * 115 + 2 * 75
P = 230 + 150
P = 380
Perimeter of a square
P = 4*s Substitute
4s = 380 Divide by 4
s = 95
Check
Area of original Rectangle = 115 * 75 = 8625
Area of the derived square = 95^2 = 9025
An oil company fills 1 over 12 of a tank in 1 over 4 hour with gasoline. At this rate, which expression can be used to determine how long it will take for the tank to fill completely? (1 point)
Group of answer choices
1 over 4⋅ 1 over 12
1 over 12⋅ 4
1 over 4⋅ 12
12 ⋅ 4
Answers
The expression that can be used to determine how long it will take for the tank to fill completely is C. 1 over 4 . 12.
How to illustrate the rate?Ratio demonstrates how many times one number can fit into another number. Ratios contrast two numbers by ordinarily dividing them. A/B will be the formula if one is comparing one data point (A) to another data point (B). This indicates that you're dividing information A by B. For instance, the ratio will be 5/10 if A is 5 and B is 10.
In this case, the oil company fills 1 over 12 of a tank in 1 over 4 hour with gasoline.
The rate will be:
= 1/4 ÷ 1/12
= 1/4 × 12
= 3
The correct option is C
Learn more about ratio on:
brainly.com/question/2328454
#SPJ1
Fill in the table using this function rule
y=28-3x

Answers
Answer:
2 = 22
3 = 19
5 = 13
6 = 10
Step-by-step explanation:
To help with future questions, take whatever is for the x and plug it into the equation
Answer:
22,19,13,10
Step-by-step explanation:
First, Replace the x in the equation with parenthesis (), then inside of the () put the x value in the table so it would look like: y=28-3(2). Then solve by multiplying 2 by 3 so you have y=28-6. Then just subtract 6 from 28 to get 22. Rinse and repeat for the rest of the values. Your first value will be 22, second 19, third 13, and lastly 10. Hope this helps!
Determine which of the following graphs does not represent a function.


Answers
Answer:
Graph b.
Step-by-step explanation:
B is not a function because it fails the vertical line test.
To be a function any vertical line drawn must pass through the graph at one point only. That is not true for graph B - a line can pass through 2 points on this graph.
A cellular phone tower services a 15 mile radius. On a hiking trip, you are 9 miles east and 11 miles north of the cell tower. Are you in the region served by the tower?
Answers
The calculated distance is approximately 14.21 miles, which is less than the 15-mile radius of the cell tower. Therefore, you are within the region served by the tower.
To determine if you are within the region served by the cell tower, we can calculate the distance between your location and the tower using the Pythagorean theorem. According to the given information, you are 9 miles east and 11 miles north of the cell tower.
Using the Pythagorean theorem, the distance from your location to the cell tower can be calculated as follows:
Distance = √((east distance)^2 + (north distance)^2)
= √((9 miles)^2 + (11 miles)^2)
= √(81 + 121)
= √202
≈ 14.21 miles
The calculated distance is approximately 14.21 miles, which is less than the 15-mile radius of the cell tower. Therefore, you are within the region served by the tower.
Learn more about the Pythagorean theorem:
https://brainly.com/question/343682
#SPJ11
Solve each formula for the indicated variable. R(r² + r₂) = r² r₂ , for r₂
Answers
According to the given statement the solution for r₂ in the given equation is (-Rr²) / (R - r²).
To solve the formula R(r² + r₂) = r² r₂ for r₂, we need to isolate the variable r₂.
1. Distribute R to the terms inside the parentheses:
R * r² + R * r₂ = r² * r₂
2. Simplify the equation:
Rr² + Rr₂ = r²r₂
3. Move all the terms containing r₂ to one side of the equation by subtracting Rr₂ from both sides:
Rr₂ - r²r₂ = -Rr²
4. Factor out r₂ from the left side of the equation:
r₂(R - r²) = -Rr²
5. Finally, solve for r₂ by dividing both sides of the equation by (R - r²):
r₂ = (-Rr²) / (R - r²)
The solution for r₂ in the given equation is (-Rr²) / (R - r²).
To know more about equation visit:
https://brainly.com/question/29657983
#SPJ11
We solved the given formula R(r² + r₂) = r² r₂ for r₂ and obtained the equation r₂ = -Rr² / (R - r²). This formula allows us to calculate the value of r₂ based on the values of R and r².
To solve the formula R(r² + r₂) = r² r₂ for r₂, we can follow these steps:
1. Distribute R to both terms inside the parentheses:
R * r² + R * r₂ = r² r₂
2. Simplify the equation by multiplying:
Rr² + Rr₂ = r² r₂
3. Move all the terms involving r₂ to one side of the equation:
Rr₂ - r² r₂ = -Rr²
4. Factor out r₂ from the left side of the equation:
r₂ (R - r²) = -Rr²
5. Divide both sides of the equation by (R - r²):
r₂ = -Rr² / (R - r²)
So the formula for r₂ in terms of R and r² is:
r₂ = -Rr² / (R - r²)
In conclusion, we solved the given formula R(r² + r₂) = r² r₂ for r₂ and obtained the equation r₂ = -Rr² / (R - r²). This formula allows us to calculate the value of r₂ based on the values of R and r².
Learn more about equation from the given link:
https://brainly.com/question/30127282
#SPJ11
Can someone help solve this?

Answers
There are 2 parallel lines with the intersection. The angles of x=171° and y=9°.
Given that,
In the picture there is a diagram and we have to find the angle of x and y.
There are 2 parallel lines with the intersection.
If a transversal cuts two parallel lines, then the equivalent angles in the pair are equal.
The pair of corresponding angles are equal
x=19y
So,
We can say x and y are on the line
Then,
x+y=180°
19y+y=180°
20y=180°
y=180/20
y=9°
Now,
x=19y
x=19×9
x=171°
Therefore, the angles of x=171° and y=9°.
To learn more about angles visit: https://brainly.com/question/28451077
#SPJ1
The frequency table shows the results of a survey that asked 175 high schoolers how they learn about news stories.
What is the frequency of a tenth grader getting their news from the Internet?
And please, maybe, explain how to get to the answer so I can figure this kind of stuff out?? Thanks so much if u will :) Max points!!

Answers
Answer:
hi i think the answer shouldbe 34/43 as its out of 43 and there is 34 people on the internet. I think this should be write but it may be wrong. if this is right please vote for brainliest. i hope my answer is right and this helps bye.
Which equation can be solved by using this system of equations?
[y-3x³-7x² +5
[y=7x²+2x
3x³-7x²+5=0
3x³-7x² +5-7x4 + 2x
7x²+2x=0
7x4+3x3-7x²+2x+5=0
Answers
The equation which can be solved by using the given system of equations; y = 3x³ - 7x² + 5 and y = 7x^4 + 2x is 3x³ - 7x² + 5 = 7x^4 + 2x. Option B is correct.
We are given;
y = 3x³ - 7x² + 5
y = 7x^4 + 2x
We will solve the given equation by substitution method:
Using the substitution method, let us substitute y = 7x^4 + 2x in the equation y = 3x³ - 7x² + 5, we get,
3x³ - 7x² + 5 = 7x^4 + 2x
So, 3x³ - 7x² + 5 = 7x^4 + 2x will be solved by using the given system of equations.
Thus, the equation which can be solved by using the given system of equations; y = 3x³ - 7x² + 5 and y = 7x^4 + 2x is 3x³ - 7x² + 5 = 7x^4 + 2x. Option B is correct.
To learn more about substitution method visit:
https://brainly.com/question/14619835
#SPJ1
A population has a mean of 53 and a standard deviation of 21. A sample of 49 observations will be taken. The probability that the sample mean will be greater than 57.95 is ___. a. 0.450 b. 0.9505 c. 0.0495 d. 0
Answers
The probability that the sample mean will be greater than 57.95 is 0.0495.
What is probability?Probability means possibility. It is a branch of mathematics that deals with the occurrence of a random event. The value is expressed from zero to one. This is the basic probability theory, which is also used in the probability distribution.
To solve this question, we need to know the concepts of the normal probability distribution and of the central limit theorem.
Normal probability distributionProblems of normally distributed samples can be solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the z-score of a measure X is given by:
\(Z=\dfrac{X-\mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
Central Limit TheoremThe Central Limit Theorem establishes that, for a random variable X, with mean \(\mu\) and standard deviation \(\sigma\), a large sample size can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(\frac{\sigma}{\sqrt{\text{n}} }\).
In this problem, we have that:
\(\mu=53,\sigma=21,\text{n}=49,\text{s}=\frac{21}{\sqrt{49} }=3\)The probability that the sample mean will be greater than 57.95
This is 1 subtracted by the p-value of Z when X = 57.95. So
\(Z=\dfrac{X-\mu}{\sigma}\)
By the Central Limit Theorem
\(Z=\dfrac{X-\mu}{\text{s}}\)
\(Z=\dfrac{57.95-53}{3}\)
\(Z=1.65\)
\(Z=1.65\) has a p-value of 0.9505.
Therefore, the probability that the sample mean will be greater than 57.95 is 1-0.9505 = 0.0495
To know more about the probability visit:
https://brainly.com/question/31321667
Someone help me please

Answers
Step-by-step explanation:
the ratio of 1/18 simply means that 1 inch in the drawing represents 18 inches in reality.
so, the real flag is therefore
2×18 = 36 inches long and 1×18 = 18 inches wide (or high).
the area of the actual flag is therefore
36 × 18 = 648 in²
you can rent time on computers at the local copy center for a $10 setup charge and an additional $2 for every 5 minutes. how much time can you rent for $25?
Answers
You can rent time on computers at the local copy center for 35 minutes with $25.
To find out how much time you can rent for $25 at the local copy center, follow these steps:
1. Subtract the $10 setup charge from the total amount you have: $25 - $10 = $15.
2. Now you have $15 left for renting time on the computers. Since it costs $2 for every 5 minutes, you need to find out how many 5-minute increments can be covered by $15.
3. Divide the remaining amount by the cost per 5-minute increment: $15 / $2 = 7.5. Since you can't have half an increment, round down to 7.
4. Multiply the number of 5-minute increments by the time per increment: 7 * 5 = 35 minutes.
So, you can rent time on computers at the local copy center for 35 minutes with $25.
To learn more about rent
https://brainly.com/question/28452806
#SPJ11
Need this quick ! Correct answers appreciated
(Selected answer is not known to be correct it just won’t let me un select an answer)

Answers
\( \qquad \qquad \bf \huge\star \: \: \large{ \underline{Answer} } \huge \: \: \star\)
\(\qquad❖ \: \sf \:g(f( - 5)) = 5\)
\(\textsf{\underline{\underline{Steps to solve the problem} }:}\)
\(\qquad❖ \: \sf \:f(x) = |2x + 9| \)
\(\qquad❖ \: \sf \:f( - 5) = |2( - 5) + 9| \)
\(\qquad❖ \: \sf \:f( - 5) = | - 10+ 9| \)
\(\qquad❖ \: \sf \:f( - 5) = | - 1| \)
\(\qquad❖ \: \sf \:f( - 5) = 1\)
next,
g(f(-5)) represents value of y at x = f(-5) = 1
hence,
\( \qquad \large \sf {Conclusion} : \)
\(\sf \:g(f( - 5)) = 5\)8) Simplify.
5(3x – 3) + 4(6x - 12)
Answers
Answer:
39x - 63
Step-by-step explanation:
5(3x - 3) + 4(6x - 12) ← distribute both parenthesis
= 15x - 15 + 24x - 48 ← collect like terms
= 39x - 63
An automatic machine in a manufacturing process is operating groperly if the iengths of an important subcomponent are normally distributed with a mean of izal cri and a otandard deviation of 5.6 cm. A. Find the probability that one selected subcomponent is longer than 122 cm, Probability = B3. Find the probability that if 3 subcomponents are randomly selected, their mean length exceeds 122 cm. Probability win C. Find the probabilify that if 3 are randomly selected, ail 3 have lengths that exceed 122 cm. Probability =
Answers
A. The probability that one selected subcomponent is longer than 122 cm can be found by calculating the area under the normal distribution curve to the right of 122 cm. We can use the z-score formula to standardize the value and then look up the corresponding probability in the standard normal distribution table.
z = (122 - μ) / σ = (122 - 100) / 5.6 = 3.93 (approx.)
Looking up the corresponding probability for a z-score of 3.93 in the standard normal distribution table, we find that it is approximately 0.9999. Therefore, the probability that one selected subcomponent is longer than 122 cm is approximately 0.9999 or 99.99%.
B. To find the probability that the mean length of three randomly selected subcomponents exceeds 122 cm, we need to consider the distribution of the sample mean. Since the sample size is 3 and the subcomponent lengths are normally distributed, the distribution of the sample mean will also be normal.
The mean of the sample mean will still be the same as the population mean, which is 100 cm. However, the standard deviation of the sample mean (also known as the standard error) will be the population standard deviation divided by the square root of the sample size.
Standard error = σ / √n = 5.6 / √3 ≈ 3.24 cm
Now we can calculate the z-score for a mean length of 122 cm:
z = (122 - μ) / standard error = (122 - 100) / 3.24 ≈ 6.79 (approx.)
Again, looking up the corresponding probability for a z-score of 6.79 in the standard normal distribution table, we find that it is extremely close to 1. Therefore, the probability that the mean length of three randomly selected subcomponents exceeds 122 cm is very close to 1 or 100%.
C. If we want to find the probability that all three randomly selected subcomponents have lengths exceeding 122 cm, we can use the probability from Part A and raise it to the power of the sample size since we need all three subcomponents to satisfy the condition.
Probability = (0.9999)^3 ≈ 0.9997
Therefore, the probability that if three subcomponents are randomly selected, all three of them have lengths that exceed 122 cm is approximately 0.9997 or 99.97%.
Based on the given information about the normal distribution of subcomponent lengths, we calculated the probabilities for different scenarios. We found that the probability of selecting a subcomponent longer than 122 cm is very high at 99.99%. Similarly, the probability of the mean length of three subcomponents exceeding 122 cm is also very high at 100%. Finally, the probability that all three randomly selected subcomponents have lengths exceeding 122 cm is approximately 99.97%. These probabilities provide insights into the performance of the automatic machine in terms of producing longer subcomponents.
To know more about probability follow the link:
https://brainly.com/question/251701
#SPJ11
6. A pizza's original price is $11. It is on sale for $9.25. What percent off is it?
Answers
Solution:
We know that:
\(Original \ price = \$11\)
\(Sale \ price = \$9.25\)
\(\frac{9.25}{11} + \frac{1.75}{11} =100\%\)
Simplify the equation to find the percent off:
\(\frac{9.25}{11} + \frac{1.75}{11} =100\%\)
\(84\% + \bold{16\%} = 100\% \space\ \space\ \space\ \ \ \ \ [Rounded]\)
This means that the original price has decreased about 16%.