Determine 2 angles, to the nearest degree, between 0° and 360° for the given trigonometric ratio (K:2, T: 2, C: 2, A: 2)
a) sinθ = 0.891
b) cosβ = 0.97437
detailed step by step please

Answers
The question is an illustration of trigonometry identity
The angles are 63 and 117 degreesThe angles are 13 and 283 degreesThe trigonometry identities are given as:
\(\sin(\theta) = 0.891\)
\(\cos(\beta) = 0.97437\)
For \(\sin(\theta) = 0.891\), take arc sine of both sides
\(\theta = \sin^{-1}(0.891)\)
Using a calculator, we have:
\(\theta = 63.0^o\)
Because the trigonometry identity is a sine ratio, and the sine of angle is positive in the first and second quadrants.
So, the other angle is in the second quadrant, and it is calculated using:
\(\theta = 180 - Angle\)
So, we have:
\(\theta = 180^o - 63.0^o\)
\(\theta = 117.0^o\)
Hence, the angles are 63 and 117 degrees
For \(\cos(\beta) = 0.97437\), take arc cosine of both sides
\(\beta = \cos^{-1}(0.97437)\)
Using a calculator, we have:
\(\beta = 13.0^o\)
Because the trigonometry identity is a cosine ratio, and the cosine of angle is positive in the first and fourth quadrants.
So, the other angle is in the fourth quadrant, and it is calculated using:
\(\beta= 270 + Angle\)
So, we have:
\(\beta= 270^o +13.00^o\)
\(\beta= 283.00^o\)
Hence, the angles are 13 and 283 degrees
Read more about trigonometry identities at:
https://brainly.com/question/10270672
Related Questions
A box has a width of 12 cm, a length of 30 cm, and a height of 16 cm. Which expression below can be used to determine the surface are oa f the box?
a
2(12 x 30) + 2(12 x 16) + 2(30 x 16)
b
2(12 + 30) + 2(12 +16) + 2(30 x 16)
c
2(12 x 30) + 2(12 x 12) + 2(30 x 16)
d
(12 x 30) + (12 x 16) + (30 x 16)
Answers
Answer:
a
Step-by-step explanation:
The area of each side is length * width:
2( 12 * 30 + 12 * 16 + 16 * 30)
which we can rewrite as 2( 12 * 30) + 2( 12 * 16) + 2 * ( 30 * 16)
How do you find the inverse of a 3 matrix?
Answers
Answer:
Inverse of a 3 by 3 Matrix
MM-1 = M-1 M = I.
Step 1: The first step while finding the inverse matrix is to check whether the given matrix is invertible. ...
Step 2: Calculate the determinant of 2 × 2 minor matrices.
Step 3: Formulate the cofactor matrix.
Step-by-step explanation:
The inverse matrix formula, A-¹ = (1/|A|) Adj A, is used to determine the inverse of a 3×3 matrix.
What is Inverse of Matrix ?The multiplicative identity is obtained by multiplying the provided matrix by the other matrix which serves as the inverse of a matrix. A matrix's inverse is A-1, since the I is the identity matrix, A A-1 = A-1 A = I.
How can I determine the 3X3 Matrix's inverse?The formula A-1 = (adj A)/(det A), where det A is in the denominator, is used to determine the inverse of a 3x3 matrix A.
• adj A = The adjoint matrix of A
• det A = determinant of A
dAs a result, det A should not be 0 for A-1 to exist. i.e.,
• A-1 exists when det A ≠ 0 (i.e., when A is nonsingular)
• A-1 does not exist when det A = 0 (i.e., when A is singular).
To know more about inverse matrix :
https://brainly.com/question/4017205
#SPJ4
Please help me solve this!
Will give Brainliest!
Please help quickly!

Answers
Answer:
y = 6.5
Step-by-step explanation:
Using a ratio
10 13
----- = -----------
10+5 13+y
10 13
----- = -----------
15 13+y
Using cross products
10(13+y) = 13*15
10(13+y) = 195
130+10y = 195
Subtract 130 from each side
10y = 65
Divide by 10
y = 65/10
y = 6.5
what is the purpose of a variable? a. to assign values b. to perform calculations c. to hold a value d. to hold a constant value
Answers
The purpose of a variable is to hold and represent a value Option C.
The purpose of a variable in programming or mathematics is to hold and represent a value that can be assigned, changed, and used in various operations or calculations. Variables are fundamental components of programming languages and mathematical equations, enabling flexibility and dynamic behavior in computational tasks.
Option (c) "to hold a value" is the most accurate answer, as variables are used to store data or information in memory locations. This value can be of different types, such as integers, floating-point numbers, characters, or even more complex data structures like arrays or objects.
Variables allow programmers to work with and manipulate data efficiently. By assigning values to variables, we can reference and modify them throughout the program, making it easier to manage and organize information.
Variables also play a crucial role in performing calculations, as mentioned in option (b). We can use variables in mathematical expressions and algorithms to perform arithmetic operations, comparisons, and other computations. By storing values in variables, we can reuse them in multiple calculations and update them as needed.
While option (a) "to assign values" is a specific use case of variables, it is not the sole purpose. Variables not only store values but also facilitate data manipulation, control flow, and the implementation of algorithms and logic.
Option (d) "to hold a constant value" is incorrect because variables, by definition, can hold varying values. Constants, on the other hand, are fixed values that do not change during the execution of a program. Option C is correct.
For more such question on variable. visit :
https://brainly.com/question/28248724
#SPJ8
marty has 1 1/3 jugs of apple juice. he uses 3/4 of the juice to make freeze pops. what fraction amount of a jus doe marty have?
Answers
Answer:
He has 1/3 of a jug left.
Step-by-step explanation:
He starts with 1 1/3 jugs.
He uses 3/4 of 1 1/3 jugs.
A full amount is 1 or 4/4. If he uses 3/4, he has 1/4 left since
1 - 3/4 = 4/4 - 3/4 = 1/4
That means he has 1/4 of 1 1/3 jugs left.
We need to multiply 1/4 by 1 1/3.
1/4 * 1 1/3 =
= 1/4 * 4/3
= 4/12
= 1/3
Answer: He has 1/3 of a jug left.
6. A trader sold 100 boxes of fruit at
GH¢8. 00 per box, 800 boxes at GH¢6. 00
per box and 600 boxes at GH¢4. 00 per
box. Find the average selling price per
box.
Answers
A trader sold 100 boxes of fruit at GH¢8. 00 per box, 800 boxes at GH¢6. 00 per box and 600 boxes at GH¢4. 00 per box, the average selling price per box is GH₵ 5.33.
Average selling price per box = (Total sales revenue) / (Total boxes sold)
There are 3 different types of fruit boxes sold. So, we need to find the total revenue from each type of fruit box sold and add them together. Similarly, we need to find the total boxes sold of all the types of fruit boxes sold and add them together. Lastly, divide the total revenue by the total boxes sold to find the average selling price per box.
1. For 100 boxes sold at GH₵ 8.00 per box, the total sales revenue is:
GH₵ 8.00 × 100 = GH₵ 8002.
For 800 boxes sold at GH₵ 6.00 per box, the total sales revenue is
GH₵ 6.00 × 800 = GH₵ 4,8003.
For 600 boxes sold at GH₵ 4.00 per box, the total sales revenue is
GH₵ 4.00 × 600 = GH₵ 2,400
Total sales revenue from all types of fruit boxes sold = GH₵ 800 + GH₵ 4,800 + GH₵ 2,400= GH₵ 8,000
Total boxes sold from all types of fruit boxes sold = 100 + 800 + 600= 1,500
Average selling price per box = (Total sales revenue) / (Total boxes sold)= GH₵ 8,000 / 1,500= GH₵ 5.33.
You can learn more about selling prices at: brainly.com/question/29065536
#SPJ11
If sin Θ = 5 over 6, what are the values of cos Θ and tan Θ?
Answers
Answer:
Check explanation
Step-by-step explanation:
Sin∅=5/6
Opp=5. Hyp=6
Adj= (√6²+5²)
= √11
Cos∅=(√11)/6
Tan∅=5/(√11)
Explanation:
sin inverse is restricted to the first and fourth quadrant, so the other side of the triangle is positive sqrt(11) by the Pythagorean theorem.
Help please I don’t understand

Answers
What is the measure of XYZ?
V
33
Y
O D. 54°
N
X
75⁰
O A. 33°
OB. 75°
O C. 108°
Answers
Reorganize os termos
2x=64
Divida ambos os membros
Solução
x=32
What is a "gestalt"? How do the experimental examples provided in the text (Necker cube, visual cliff, etc.) help demonstrate principles of perceptual organization?; choose one example to discuss specifically.
Answers
The Kanizsa triangle illusion helps us understand that our perceptual experiences are not simply the sum of the individual sensory inputs, but rather the result of a complex and variable process of perceptual organization.
Gestalt is a German word meaning "shape" or "form," and in psychology, it refers to a set of principles that describe how people perceive and organize sensory information into meaningful wholes. These principles propose that the whole is greater than the sum of its parts, and that we tend to organize our perceptual experiences into coherent, holistic forms rather than isolated, unrelated sensations.
Experimental examples such as the Necker cube, visual cliff, and others help demonstrate principles of perceptual organization by highlighting how our minds naturally try to impose structure and order on sensory input. For example, the Necker cube is a two-dimensional drawing that can be perceived as a cube that can be viewed from different angles. However, as one stares at the image, it appears to flip back and forth between different possible interpretations. This phenomenon illustrates the Gestalt principle of figure-ground, which describes how we tend to perceive objects as being distinct from their surrounding context.
To know more about variable,
https://brainly.com/question/2466865
#SPJ11
please help me answer number 3 !!!

Answers
Answer:
Prime factorization method.(Table method)Step-by-step explanation:
Answer& Step-by-step explanation:
To multiply powers of the same base, add their exponents.
5d³ / 3f
How would I solve this?
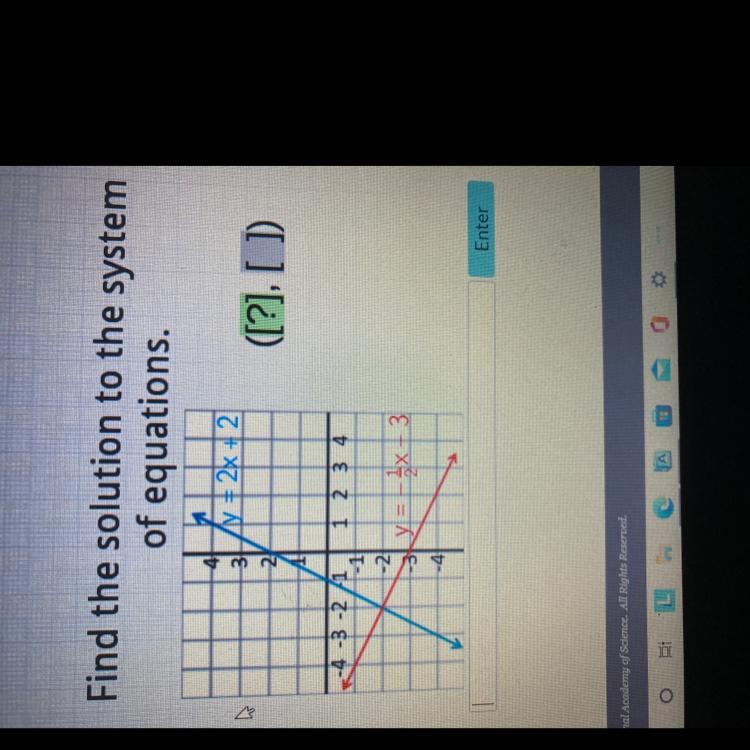
Answers
Answer:
(-2, -2)
Step-by-step explanation:
the solution of the system of equation put simply is the point of intersection between the 2 lines
hence, the answer is (-2,-2)
Help me on this it’s in the picture

Answers
Answer:
x = -2
y = 3
Step-by-step explanation:
from above equation we get ,
=》y = 3x + 9
now ,
by second equation,
=》2x + 3y = 5
=》2x + 3 × ( 3x + 9 ) = 5
( since, y = 3x + 9 , by equation 1 )
=》2x + 9x + 27 = 5
=》11x = -22
=》x = -2
putting value of x in equation 1 ;
=》 y = 3x + 9
=》 y = 3 × ( -2 ) + 9
=》 y = -6 + 9
=》 y = 3
y=3
The Land of Nod lies in the monsoon zone, and has just two seasons, Wet and Dry. The Wet season lasts for 1/3 of the year, and the Dry season for 2/3 of the year. During the Wet season, the probability that it is raining is 3/4; during the Dry season, the probability that it is raining is 1/6. (a) I visit the capital city, Oneirabad, on a random day of the year. What is the probability that it is raining when I arrive? (b) I visit Oneirabad on a random day, and it is raining when I arrive. Given this information, what is the probability that my visit is during the Wet season? (c) I visit Oneirabad on a random day, and it is raining when I arrive. Given this information, what is the probability that it will be raining when I return to Oneirabad in a year's time? (You may assume that in a year's time the season will be the same as today but, given the season, whether or not it is raining is independent of today's weather.)
Answers
Answer:
Step-by-step explanation:
(a) To find the probability that it is raining when you arrive in Oneirabad on a random day, we need to use the law of total probability.
Let A be the event that it is raining, and B be the event that it is the Wet season.
P(A) = P(A|B)P(B) + P(A|B')P(B')
Given that the Wet season lasts for 1/3 of the year, we have P(B) = 1/3. The probability that it is raining during the Wet season is 3/4, so P(A|B) = 3/4.
The Dry season lasts for 2/3 of the year, so P(B') = 2/3. The probability that it is raining during the Dry season is 1/6, so P(A|B') = 1/6.
Now we can calculate the probability that it is raining when you arrive:
P(A) = (3/4)(1/3) + (1/6)(2/3)
= 1/4 + 1/9
= 9/36 + 4/36
= 13/36
Therefore, the probability that it is raining when you arrive in Oneirabad on a random day is 13/36.
(b) Given that it is raining when you arrive, we can use Bayes' theorem to calculate the probability that your visit is during the Wet season.
Let C be the event that your visit is during the Wet season.
P(C|A) = (P(A|C)P(C)) / P(A)
We already know that P(A) = 13/36. The probability that it is raining during the Wet season is 3/4, so P(A|C) = 3/4. The Wet season lasts for 1/3 of the year, so P(C) = 1/3.
Now we can calculate the probability that your visit is during the Wet season:
P(C|A) = (3/4)(1/3) / (13/36)
= 1/4 / (13/36)
= 9/52
Therefore, given that it is raining when you arrive, the probability that your visit is during the Wet season is 9/52.
(c) Given that it is raining when you arrive, the probability that it will be raining when you return to Oneirabad in a year's time depends on the season. If you arrived during the Wet season, the probability of rain will be different from if you arrived during the Dry season.
Let D be the event that it is raining when you return.
If you arrived during the Wet season, the probability of rain when you return is the same as the probability of rain during the Wet season, which is 3/4.
If you arrived during the Dry season, the probability of rain when you return is the same as the probability of rain during the Dry season, which is 1/6.
Since the season you arrived in is independent of the weather when you return, we need to consider the probabilities based on the season you arrived.
Let C' be the event that your visit is during the Dry season.
P(D) = P(D|C)P(C) + P(D|C')P(C')
Since P(C) = 1/3 and P(C') = 2/3, we can calculate:
P(D) = (3/4)(1/3) + (1/6)(2/3)
= 1/4 + 1/9
= 9/36 + 4/36
= 13/36
Therefore, the probability that it will be raining when you return to Oneirabad in a year's time, given that it is raining when you arrive, is 13/36.
To know more about probability refer here:
https://brainly.com/question/32117953
#SPJ11
7. A farmer wants to start raising cows, horses, goats, and sheep, and desires to have a rectangular pasture for the animals to graze in. However, no two different kinds of animals can graze together. In order to minimize the amount of fencing she will need, she has decided to enclose a large rectangular area and then divide it into four equally sized pens by adding three segments of fence inside the large rectangle that are parallel to two existing sides. She has decided to purchase 7500 ft of fencing. What is the maximum possible area that each of the four pens will enclose?
Answers
Having a rectangular pasture for the animals to graze in is something a farmer wants in order to start growing cows, horses, goats, and sheep. She has decided to purchase 7500 ft of fencing. 1875 square feet is the maximum possible area that each of the four pens will enclose.
The maximum possible area of each pen is 1875 square feet. To calculate this, first calculate the total area of the large rectangle that the farmer is enclosing. To do this, multiply the total length of the fencing (7500 feet) by the width of the fence (1 foot). This gives us 7500 square feet as the area of the large rectangle.
Next, divide the area of the large rectangle by 4 to get the area of each pen. This gives us 1875 square feet as the maximum area of each pen.
Total Area of Large Rectangle = 7500 ft x 1 ft = 7500 sq ft
Area of Each Pen = 7500 sq ft / 4 = 1875 sq ft
Learn more about area here
https://brainly.com/question/27683633
#SPJ4
The sum of ages of Clayman and Ato is 25 years. In five years' time, the age of Ato will twice the age of Clayman now. a. How old is Clayman? b. How old is Ato?
Answers
Clayman is 10 years old and Ato is 15 years old
Word problems leading to equationsLet the age of Clayman be x
Let the age of Ato be y
If the sum of ages of Clayman and Ato is 25 years. then;
x + y = 25
x = 25 - y ...... 1
In five years time;
Age of Clayman = x + 5
Age of Ato = y + 5
If in five years' time, the age of Ato will twice the age of Clayman now, then;
y+5 = 2x ............. 2
Substitute equation 1 into 2
y +5 = 2(25-y)
y + 5 = 2(30 - y)
y + 5 = 50 - 2y
3y = 45
y = 15
Since x + y = 25
x = 25 - 15
x = 10
Therefore Clayman is 10 years old and Ato is 15 years old
Learn more on system of equation here:
#SPJ1https://brainly.com/question/14323743
what must be your average speed in order to travel 350 km in 5.15 h?
Answers
Answer:
68 km/h--------------
Average speed equation:
s = d/t, where d- total distance, t - total timeSubstitute 350 for d and 5.15 for t:
s = 350/5.15s = 67.96 ≈ 68 km/hThe average speed must be approximately 68 km per hour.
For f(x) =2x, find a formula for the Riemann sum obtained by dividing the interval [2.5] subintervals and using the right hand endpoint for each ck. Simplify the sum and take the limit as n--> infinity to calculate the area under the curve over [2,5]
please show all of your work as be as descriptive as you can I appreciate your help thank you!
Answers
The area under the curve over [2,5] is 24.
Given function is f(x) = 2xIntervals [2, 5] is given and it is to be divided into subintervals.
Let us consider n subintervals. Therefore, width of each subinterval would be:
$$
\Delta x=\frac{b-a}{n}=\frac{5-2}{n}=\frac{3}{n}
$$Here, we are using right-hand end point. Therefore, the right-hand end points would be:$${ c }_{ k }=a+k\Delta x=2+k\cdot\frac{3}{n}=2+\frac{3k}{n}$$$$
\begin{aligned}
\therefore R &= \sum _{ k=1 }^{ n }{ f\left( { c }_{ k } \right) \Delta x } \\&=\sum _{ k=1 }^{ n }{ f\left( 2+\frac{3k}{n} \right) \cdot \frac{3}{n} }\\&=\sum _{ k=1 }^{ n }{ 2\cdot\left( 2+\frac{3k}{n} \right) \cdot \frac{3}{n} }\\&=\sum _{ k=1 }^{ n }{ \frac{12}{n}\cdot\left( 2+\frac{3k}{n} \right) }\\&=\sum _{ k=1 }^{ n }{ \frac{24}{n}+\frac{36k}{n^{ 2 }} }\\&=\frac{24}{n}\sum _{ k=1 }^{ n }{ 1 } +\frac{36}{n^{ 2 }}\sum _{ k=1 }^{ n }{ k } \\&= \frac{24n}{n}+\frac{36}{n^{ 2 }}\cdot\frac{n\left( n+1 \right)}{2}\\&= 24 + \frac{18\left( n+1 \right)}{n}
\end{aligned}
$$Take limit as n → ∞, so that $$
\begin{aligned}
A&=\lim _{ n\rightarrow \infty }{ R } \\&= \lim _{ n\rightarrow \infty }{ 24 + \frac{18\left( n+1 \right)}{n} } \\&= \boxed{24}
\end{aligned}
$$
To know more about area :
https://brainly.com/question/30307509
#SPJ11
Given function f(x) = 2x. The interval is [2,5]. The number of subintervals, n is 3.
Therefore, the area under the curve over [2,5] is 21.
From the given data, we can see that the width of the interval is:
Δx = (5 - 2) / n
= 3/n
The endpoints of the subintervals are:
[2, 2 + Δx], [2 + Δx, 2 + 2Δx], [2 + 2Δx, 5]
Thus, the right endpoints of the subintervals are: 2 + Δx, 2 + 2Δx, 5
The formula for the Riemann sum is:
S = f(c1)Δx + f(c2)Δx + ... + f(cn)Δx
Here, we have to find a formula for the Riemann sum obtained by dividing the interval [2.5] subintervals and using the right hand endpoint for each ck. The width of each subinterval is:
Δx = (5 - 2) / n
= 3/n
Therefore,
Δx = 3/3
= 1
So, the subintervals are: [2, 3], [3, 4], [4, 5]
The right endpoints are:3, 4, 5. The formula for the Riemann sum is:
S = f(c1)Δx + f(c2)Δx + ... + f(cn)Δx
Here, Δx is 1, f(x) is 2x
∴ f(c1) = 2(3)
= 6,
f(c2) = 2(4)
= 8, and
f(c3) = 2(5)
= 10
∴ S = f(c1)Δx + f(c2)Δx + f(c3)Δx
= 6(1) + 8(1) + 10(1)
= 6 + 8 + 10
= 24
Therefore, the Riemann sum is 24.
To calculate the area under the curve over [2, 5], we take the limit of the Riemann sum as n → ∞.
∴ Area = ∫2^5f(x)dx
= ∫2^52xdx
= [x^2]2^5
= 25 - 4
= 21
Therefore, the area under the curve over [2,5] is 21.
To know more about Riemann sum visit
https://brainly.com/question/31737945
#SPJ11
Policies Current Attempt in Progress On May 1, 2021, Sheffield Company sells office furniture for $300000 cash. The office furniture originally cost $746800 when purchased on January 1, 2014. Depreciation is recorded by the straight-line method over 10 years with a salvage value of $80200. What gain should be recognized on the sale? (Hint: Use 7.333333 for years used in calculation.) O $44540. O $22220. O $84080. O $42040. Save for Later -/5 = 1 Attempts: 0 of 1 used Submit Answer
Answers
To calculate the gain on the sale of the office furniture, we need to determine the asset's book value and compare it to the sale price.
First, let's calculate the accumulated depreciation on the furniture. The furniture was purchased on January 1, 2014, and the straight-line depreciation method is used over 10 years with a salvage value of $80,200.
Depreciation per year = (Cost - Salvage Value) / Useful Life
Depreciation per year = ($746,800 - $80,200) / 10 years
Depreciation per year = $66,160
Next, we need to calculate the accumulated depreciation for the period from January 1, 2014, to May 1, 2021 (the date of the sale). This is approximately 7.33 years.
Accumulated Depreciation = Depreciation per year × Years
Accumulated Depreciation = $66,160 × 7.33 years
Accumulated Depreciation = $484,444.80
Now, we can calculate the book value of the furniture:
Book Value = Cost - Accumulated Depreciation
Book Value = $746,800 - $484,444.80
Book Value = $262,355.20
Finally, we can calculate the gain on the sale:
Gain on Sale = Sale Price - Book Value
Gain on Sale = $300,000 - $262,355.20
Gain on Sale = $37,644.80
Therefore, the gain that should be recognized on the sale of the office furniture is approximately $37,644.80.
To know more about depreciation, refer here:
https://brainly.com/question/30531944
#SPJ11
The gain that should be recognized on the sale of the office furniture is $84,080.
The gain is calculated by subtracting the equipment's book value from the sale price. This gain will be reported on the company's income statement. Here is how to calculate the gain:First, find the equipment's book value using the straight-line method of depreciation.
Straight-line depreciation is calculated by taking the difference between the equipment's original cost and its salvage value, and then dividing it by the number of years the equipment is used. The annual depreciation expense is then multiplied by the number of years the equipment is used to find the equipment's book value at the end of its useful life.
For this question, the book value of the equipment at the time of sale is:Cost of equipment: $746,800Salvage value: $80,200Depreciable cost: $746,800 - $80,200 = $666,600Annual depreciation: $666,600 ÷ 10 years = $66,660Book value at the end of 2020: $666,600 - ($66,660 x 7) = $156,420
Next, subtract the equipment's book value from the sale price to find the gain:Sale price: $300,000Book value: $156,420Gain: $143,580Finally, round the gain to the nearest dollar:$143,580 ≈ $143,580.00So the gain that should be recognized on the sale of the office furniture is $84,080.
learn more about gain here:
https://brainly.com/question/31218742
#SPJ11
How many three-digit positive integers \(x\) satisfy \(3874x+481\equiv 1205 \pmod{23}\)
Answers
Answer:
40
Step-by-step explanation:
Any solution x will mod 23 will also have x+23n as a solution, for some integer n. Since 900/23 = 39 3/23, we know there are 39 or 40 three-digit integers of this form.
As it happens, 100 is the smallest 3-digit solution. So, there are 40 three-digit numbers that are of the form 100 +23n, hence 40 solutions to the equation.
_____
The equation reduces, mod 23, to ...
10x = 11
Its solutions are x = 23n +8.
Mutpliy please I need to finish this:)

Answers
Answer: 1. p^24 2. r^7 3. s^35 4. u^13
Step-by-step explanation: Hope this helps!
Find the surface area of the prism.

Answers
Answer:
30 i think
Step-by-step explanation:
Which graph shows the image being rotated 90°?
Answers
Answer:
There is no picture, my sweetheart.
Step-by-step explanation:
A city has a population of 230,000 people. Suppose that each year the population grows by 9%. What will the population be after 6 years? Use the calculator provided and round your answer to the nearest whole number.
Answers
Answer:
385,733Step-by-step explanation:
If it grows by 9% each year, you can simply do the current population times 109%. Because its an additional 9%.
230,000*109% = 250,700
After the first year, there is a population of 250,700 people.
250,700*109% = 273,263
After the second year, there is a population of 273,263 people.
273,263*109% = 297,856.67
After the third year, there is a population of 297,856.67 people.
297,856.67*109% = 324,663.77
After the fourth year, there is a population of 324,663.77 people.
324,663.77*109% = 353,883.509
After the fifth year, there is a population of 353,883.509 people.
353,883.509*109% = 385,733.025
After the sixth year, there is a population of 385,733.025 people
Round it up to 385,733 people.
HELP ME PLEASE!!!! I NEED HELP

Answers
Answer:
Angles forming a triangle sum to 180°
25. If mVYX = 276° and m angle UVX = (4x - 5),
find the value of x.
Can someone help me please

Answers
Answer:
22.25 or 22
Step-by-step explanation:
360-276+=84
4x-5=84
4x=89
x=22.25 or 22
Answer:
answer is 11. Got this pic from the internet btw.
Step-by-step explanation:
If you were to search this question up, which I’m sure you did, you would find that in the images portion, there’s an image where it shows the same question but with multiple choice answers. Among these choices is 11.

can someone please explain how to find the quotient of 405/27 fraction using long division? :)
Answers
The quotient of 405/27 fraction using division is 15.
How to calculate the fraction?It should be noted that the information is simply to divide the numbers.
In this case, the numerator is 405 and the denominator is 27
Therefore, the quotient based on the information illustrated will be:
= 405 / 27
= 15
Therefore, the quotient is 15.
Learn more about fractions on:
brainly.com/question/17220365
#SPJ1
solve for x and y pls and thank u

Answers
Answer:
fourth
Step-by-step explanation:
Angle X is the inscribed angle of the two arcs that measure 122 and 64 so
\(x = \frac{1}{2} (122 + 64)\)
\(x = \frac{1}{2} (186) = 93\)
A cyclic quadrilateral states that the opposite angles add up to 180
so
\(y = 18 0 - 83 = 97\)
The correct answer is the fourth option
toms water bottle can hold up to 32 ounces of water. each day he drinks more than 2 full bottles of water. which inequality correctly describes the number of ounces of water, w, that tom drinks each day?
Answers
The inequality that correctly describes the number of ounces of water, w, that tom drinks each day is d. 64<w.
Amount of water that the bottle can hold = 32 ounces
Bottles of water consumed = 2
A mathematical comparison and representation of the connection between two expressions is known as an inequality. It can be regarded as a generalisation of an equation and is denoted by signs such as <, > and =.
Tom consumes more than two complete bottles of water every day. Since each bottle can carry up to 32 ounces of water, we can describe Tom's daily water consumption as -
= w > 2 × 32
Therefore,
Simplifying the right side of the inequality:
w > 64
Complete Question:
Toms water bottle can hold up to 32 ounces of water. each day he drinks more than 2 full bottles of water. which inequality correctly describes the number of ounces of water, w, that tom drinks each day?
a. w>2
b. 32<w
c. w = 64
d. 64<w
Read more about inequality on:
https://brainly.com/question/24372553
#SPJ4
A gray crayon is made with 5\text{ mL}5 mL5, start text, space, m, L, end text of black wax for every 6\text{ mL}6 mL6, start text, space, m, L, end text of white wax.
Answers
Step-by-step explanation:
Given that,
A gray crayon is made with 5 mL of black wax for every 6 mL of white wax.
We need to find the mixture will create the same shade of gray.
For this we need to make the ratio same.
If we multiply 5 mL and 6 mL by 3 to make the ratio same.
5 mL × 3 = 15 mL
6 mL × 3 = 18 mL
Hence, 15 mL of black wax mixed with 18 mL of white wax is mixed so as to make the ratio same.
Answer:
15ml of black wax mixed with 18ml of white wax
35ml of black wax mixed with 42ml of white wax
Step-by-step explanation: Khan Academy