Describe the compliment of the set of odd numbers greater than 0 within the set of positive integers.
Answers
Answer:
Step-by-step explanation:
it is the set of positive even integers.
{0,2,4,...}
Related Questions
Bridget Riley was just one of many artists associated with the 1960's 'Op Art' Movement. True or false
Answers
Answer:
True
Explanation:
Bridget Riley was one of the most prominent artists associated with the 1960s 'Op Art' movement, which was an art movement that explored optical illusions and effects to create abstract art that played with the viewer's perception. However, there were many other artists associated with this movement, including Victor Vasarely, Richard Anuszkiewicz, and Yaacov Agam, among others.
Underwood Company is preparing its annual profit plan. As part of its analysis of the profitability of individual products, the controller estimates the amount of manufacturing overhead that should be assigned to each of the two product lines from the information given below. Wall Mirrors Specialty Windows Total units produced 30 30 Total number of material moves 7 18 Direct labor hours per unit 145 145 Budgeted material-handling costs are $30,000. The material-handling cost per wall mirror under activity-based costing is:
Answers
The material-handling cost per wall mirror under activity-based costing is $280
What is activity-based costing?
Activity-based costing involves absorbing overheads based on cost drivers which directly impact the incurrence of the overhead, in this case, material moves determine the amount of material-handling costs to be incurred, hence, material-handing overheads would be absorbed into the two products based on material moves, which is the appropriate cost driver.
There 25 materials move in both divisions (i.e. 7+18=25)
Material-handling cost per material move=Budgeted material-handling costs /total material moves
Budgeted material-handling costs =$30,000
Material-handling cost per material move=$30,000/25
Material-handling cost per material move=$1,200
Total material-handing costs for wall mirror=number of material moves for wall mirror*Material-handling cost per material move
Total material-handing costs for wall mirror=7*$120
Total material-handing costs for wall mirror=$8,400
material-handling cost per wall mirror=Total material-handing costs for wall mirror/number of wall mirrors
material-handling cost per wall mirror=$8,400/30
material-handling cost per wall mirror=$280
Find out more about on activity-based costing:https://brainly.com/question/14912137
#SPJ1
can anyone slove this

Answers
Answer:
your rise is 2 and your run is 7
Step-by-step explanation:
rise/run = 2/7
HELP! write y+4 =-2/3(x-9) in standard form
Answers
Explanation: I just know:)
2 Mabaso has R140, Thabo has R70 and Ally has R35. What is the ratio of the amount of money Mabaso has, to the amount of money Thabo has and to the amount of money Ally has? Write the ratios in simplest form. The price of a steel table is R750. On Black Friday the table could be bought for R600. Calculate the percentage discount? Show ALL your calculations. Convert 125 g to kilograms. (1 kg = 1 000 grams) A green grocer packs 12 apples in a plastic bag. Calculate the number of bags he w need if he has 285 apples. The scale of a map is 1 500 000. Determine the actual distance in km if measurement on the map is 23,7 cm. Hint: 1 km = 100 000 cm
Answers
The actual distance represented by 23.7 cm on the map is 355.5 km.
To find the ratio of the amount of money Mabaso has to the amount of money Thabo has and the amount of money Ally has, we can divide each amount by the smallest amount (which is R35) to simplify the ratio.
Mabaso has R140, Thabo has R70, and Ally has R35.
The ratio of Mabaso's money to Thabo's money is:
R140 ÷ R35 = 4
The ratio of Mabaso's money to Ally's money is:
R140 ÷ R35 = 4
Therefore, the ratio of the amount of money Mabaso has to the amount of money Thabo has and to the amount of money Ally has is 4:1:1.
To calculate the percentage discount of a steel table, we need to find the difference between the original price and the discounted price, and then divide it by the original price. Finally, we multiply the result by 100 to get the percentage.
Original price: R750
Discounted price: R600
Discount: R750 - R600 = R150
Percentage discount: (R150 ÷ R750) × 100 = 20%
So, the table has a 20% discount on Black Friday.
To convert 125 grams to kilograms, we divide the amount in grams by 1,000 (since there are 1,000 grams in a kilogram).
125 g ÷ 1,000 = 0.125 kg
Therefore, 125 grams is equal to 0.125 kilograms.
If a green grocer packs 12 apples in a plastic bag and has 285 apples, we divide the total number of apples by the number of apples per bag to determine the number of bags needed.
Number of bags needed: 285 apples ÷ 12 apples/bag = 23.75 bags
Since we can't have a fraction of a bag, we round up to the nearest whole number. Therefore, the green grocer would need 24 bags.
If the scale of a map is 1,500,000 and the measurement on the map is 23.7 cm, we can use the scale to determine the actual distance.
1 cm on the map represents 1,500,000 cm in reality.
23.7 cm on the map represents x cm in reality.
x = 23.7 cm × 1,500,000 cm = 35,550,000 cm
To convert cm to km, we divide by 100,000 (since there are 100,000 cm in a kilometer).
35,550,000 cm ÷ 100,000 = 355.5 km
For more such questions on distance
https://brainly.com/question/30395212
#SPJ8
????????????????????????

Answers
Answer:
\(P(Sum = 9) = \frac{1}{9}\)
Step-by-step explanation:
Given
Outcomes of rolling two dice
Required
P(Sum = 9)
From the given outcomes, we have:
\(n(S) = 36\) -- the sample size
\(Sum = 9:=\{(3,6),(4,5),(5,4),(6,3)\}\)
So.
\(n(Sum = 9) = 4\)
The probability is:
\(P(Sum = 9) = \frac{n(Sum = 9)}{n(S)}\)
\(P(Sum = 9) = \frac{4}{36}\)
Simplify
\(P(Sum = 9) = \frac{1}{9}\)
A student researcher compares the ages of cars owned by students and cars owned by faculty at a local state college. A sample of 263 cars owned by students had an average age of 7.25 years. A sample of 291 cars owned by faculty had an average age of 7.12 years. Assume that the population standard deviation for cars owned by students is 3.77 years, while the population standard deviation for cars owned by faculty is 2.99 years. Determine the 90% confidence interval for the difference between the true mean ages for cars owned by students and faculty. Step 1 of 3: Find the point estimate for the true difference between the population means.
Answers
Answer:
The point estimate for the true difference between the population means is 0.13.
The 90% confidence interval for the difference between the true mean ages for cars owned by students and faculty is between -0.35 years and 0.61 years.
Step-by-step explanation:
To solve this question, before building the confidence interval, we need to understand the central limit theorem and subtraction between normal variables.
Central Limit Theorem
The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean \(\mu\) and standard deviation \(\sigma\), the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
Subtraction between normal variables:
When we subtract two normal variables, the mean is the subtraction of the means while the standard deviation is the square root of the sum of the variances.
A sample of 263 cars owned by students had an average age of 7.25 years. The population standard deviation for cars owned by students is 3.77 years.
This means that:
\(\mu_s = 7.25, \sigma_s = 3.77, n = 263, s_s = \frac{3.77}{\sqrt{263}} = 0.2325\)
A sample of 291 cars owned by faculty had an average age of 7.12 years. The population standard deviation for cars owned by faculty is 2.99 years.
This means that:
\(\mu_f = 7.12, \sigma_f = 2.99, n = 291, s_f = \frac{2.99}{\sqrt{291}} = 0.1753\)
Difference between the true mean ages for cars owned by students and faculty.
Distribution s - f. So
\(\mu = \mu_s - \mu_f = 7.25 - 7.12 = 0.13\)
This is also the point estimate for the true difference between the population means.
\(s = \sqrt{s_s^2+s_f^2} = \sqrt{0.2325^2+0.1753^2} = 0.2912\)
90% confidence interval for the difference:
We have that to find our \(\alpha\) level, that is the subtraction of 1 by the confidence interval divided by 2. So:
\(\alpha = \frac{1 - 0.9}{2} = 0.05\)
Now, we have to find z in the Ztable as such z has a pvalue of \(1 - \alpha\).
That is z with a pvalue of \(1 - 0.05 = 0.95\), so Z = 1.645.
Now, find the margin of error M as such
\(M = zs = 1.645*0.2912 = 0.48\)
The lower end of the interval is the sample mean subtracted by M. So it is 0.13 - 0.48 = -0.35 years
The upper end of the interval is the sample mean added to M. So it is 0.13 + 0.48 = 0.61 years.
The 90% confidence interval for the difference between the true mean ages for cars owned by students and faculty is between -0.35 years and 0.61 years.
For what value of the number k is the following function differentiable at x=2
f(x) = {2x + 1 if x<2
k x=2
3x-1 x>2}
Answers
Answer:
For f(x) to be differentiable at 2, k = 5.
Step-by-step explanation:
For f(x) to be differentiable at x = 2, f(x) has to be continuous at 2.
For f(x) to be continuous at 2, the limit of f(2 – h) = f(2) = f(2 + h) as h tends to 0.
Now,
f(2 – h) = 2(2 – h) + 1 = 4 – 2h + 1 = 5 – 2h.
As h tends to 0, lim (5 – 2h) = 5
Also
f(2 + h) = 3(2 + h) – 1 = 6 + 3h – 1 = 5 + 3h
As h tends to 0, lim (5 + 3h) = 5.
So, for f(2) to be continuous k = 5
What's the midpoint between (-2, 7) and (6, 3)?A) (2, 5)B) (-1, 2)C) (3, 2)D) (-2, 6)
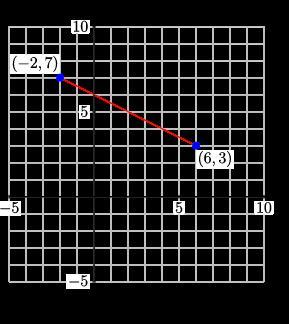
Answers
1) The midpoint of a line segment can be found by taking the average of both endpoints. So in this question, we can write out the following:
\(\begin{gathered} M=\frac{x_1+x_2}{2}.\frac{y_1+y_2}{2} \\ M=\frac{-2+6}{2},\frac{7+3}{2} \\ M=(2,5) \end{gathered}\)As we can see the midpoint divides the line segment into two halves.
Which are equivalent to each other 6a-4a+2, 2+5a+5a and 9a+a+2 WHO EVER ANSWERS I WILL MARK BRAINLIEST
Answers
Answer:
2+5a+5a and 9a+a+2
Step-by-step explanation:
It is the answer as
6a-4a+2= 2a+2
2+5a+5a= 10a+2
& 9a+a+2= 10a+2
PLEASE MARK ME AS BRAINLIEST!!!
I need help with this!

Answers
The length AC in the kite is 8.7 cm.
How to find the side AC in the kite?A kite is a quadrilateral that has two pairs of consecutive equal sides and
perpendicular diagonals. Therefore, let's find the length AC in the kite.
Hence, using Pythagoras's theorem, let's find CE.
Therefore,
7² - 4² = CE²
CE = √49 - 16
CE = √33
CE = √33
Let's find AE as follows:
5²- 4² = AE²
AE = √25 - 16
AE = √9
AE = 3 units
Therefore,
AC = √33 + 3
AC = 5.74456264654 + 3
AC = 8.74456264654
AC = 8.7 units
learn more on kite here: https://brainly.com/question/27975644
#SPJ9
A tree is 57 inches tall. How tall is it in feet and inches?
Answers
Hey there! :)
Answer:
4 ft 9 inches tall.
Step-by-step explanation:
Convert 57 inches to feet:
12 inches = 1 foot.
Therefore:
57 / 12 = 4 with a remainder of 9.
Thus, the tree is 4 ft 9 inches tall.
Answer:
4 feet 9 inches
Step-by-step explanation:
need help asap look in file attached

Answers
Answer:
length: 21 cm
width: 16 cm
Step-by-step explanation:
. A rectangle has two lengths and two widths, or two sides that are vertical (up and down) and two sides that are horizontal (left and right)
. In order to find the perimeter we must add up all four side lengths.
. You can find the perimeter of a rectangle by adding the length and the width then multiplying by 2, because there are two of each side length.
P = 2(l+w)
In the question the perimeter is given, which is 74.
We can divide 74 by 2 so that we can find the sum of the length and width.
74/2 = 37
l + w = 37
In the question is states that the length is 5 inches longer than the width.
l = (5 + w)
There are two widths and two lengths in a rectangle, the measurement of the two lengths is 5 inches longer than the two widths.
5 + w + w = 37
5 + 2w = 37
Now that we have our equation we can solve for w, or the width.
1. Move the term containing the variable to the left
5 + 2w = 37
2w + 5 = 37
2. Subtract 5 from both sides of the equation, the opposite of adding 5
2w + 5 = 37
2w + 5 - 5 = 37 - 5
2w = 32
3. Divide by 2 in both sides of the equation, the opposite of multiplying 2
2w = 32
2w/2 = 32/2
4. Cancel out the 2s on the left, but leave the x
2w/2 = 32/2
w = 16
So, now that w, or the width = 16, we can find the length:
l = 5 + w
l = 5 + 16
l = 21
You can check your answer by plugging in our values into the original perimeter formula:
P = 2(l+w)
P = 2(21 + 16)
P = 2(37)
P = 74, so my answer is correct, because 74 is the perimeter given in the question.
help me pelaseeeeeeeee

Answers
Answer: 1. x=18
2. x=21
Step-by-step explanation:
1.Q 114=7x-12
7x=126
x=18
2.Q 4x-2=3x+19
4x-3x=19+2
x=21
Answer:
Step-by-step explanation:
if im right but i think
7x-12=144 opposite sides are congruent
7x/7=156/7
X= 22.285
Keisha used a photo that measured 4 inches by 6 inches to make a copy that measured 8 inches by 12 inches. What is the scale factor of the dilation? Write your answer as a whole number or decimal.
Answers
Answer:
Below.
Step-by-step explanation:
So 4-6 to 8-12.
4 can be devised by 12, and so can 6.
4:8 6:12
If we flip them over we can find the dilation.
so?
8:4 12:6
Each can be divided by 2.
So the factor if dilation is 2.
The Dell Computer Company makes its own computers and delivers them directly to customers who order them via the Internet. To achieve its objective of speed, Dell makes each of its five most popular computers and transports them to warehouses from which it generally takes one day to deliver a computer to the customer. This strategy requires high levels of inventory that add considerably to the cost. To lower these costs the operations manager wants to use an inventory model. He notes demand during lead time is normally distributed and he needs to know the mean to compute the optimum inventory level. He observes 25 lead time periods and records the demand during each period. The manager would like a 95% confidence interval estimate of the mean demand during lead time. Assume that the manager knows that the standard deviation is 75 computers. Construct and interpret the confidence Interval Estimator.
Answers
The 95% confidence interval estimate of the mean demand during lead time is given as follows:
\(\overline{x} \pm 29.4\)
The interpretation is that we are 95% sure that the sample mean is within 29.4 computers of the population mean.
What is a z-distribution confidence interval?The bounds of the confidence interval are given by the equation presented as follows:
\(\overline{x} \pm z\frac{\sigma}{\sqrt{n}}\)
In which the parameters are given as follows:
\(\overline{x}\) is the sample mean.z is the critical value.n is the sample size.\(\sigma\) is the standard deviation for the population.The confidence level is of 95%, hence the critical value z is the value of Z that has a p-value of \(\frac{1+0.95}{2} = 0.975\), so the critical value is z = 1.96.
The remaining parameter values are given as follows:
\(\sigma = 75, n = 25\)
Hence the interval is given as follows:
\(\overline{x} \pm z\frac{\sigma}{\sqrt{n}}\)
\(\overline{x} \pm 1.96 \times \frac{75}{\sqrt{25}}\)
\(\overline{x} \pm 29.4\)
More can be learned about the z-distribution at https://brainly.com/question/25890103
#SPJ1
Three more than x is equal to 47. Find x.
Answers
Answer:
45
Step-by-step explanation:
Ion know tbh
Suppose 42% of the population has myopia. If a random sample of size 442 is selected, what is the probability that the proportion of persons with myopia will differ from the population proportion by less than 3%
Answers
Answer:
0.7994 = 79.94% probability that the proportion of persons with myopia will differ from the population proportion by less than 3%.
Step-by-step explanation:
To solve this question, we need to understand the normal probability distribution and the central limit theorem.
Normal Probability Distribution
Problems of normal distributions can be solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the z-score of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
Central Limit Theorem
The Central Limit Theorem establishes that, for a normally distributed random variable X, with mean \(\mu\) and standard deviation \(\sigma\), the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
For a proportion p in a sample of size n, the sampling distribution of the sample proportion will be approximately normal with mean \(\mu = p\) and standard deviation \(s = \sqrt{\frac{p(1-p)}{n}}\)
Suppose 42% of the population has myopia.
This means that \(p = 0.42\)
Random sample of size 442 is selected
This means that \(n = 442\)
Mean and standard deviation:
\(\mu = p = 0.42\)
\(s = \sqrt{\frac{p(1-p)}{n}} = \sqrt{\frac{0.42*0.58}{442}} = 0.0235\)
What is the probability that the proportion of persons with myopia will differ from the population proportion by less than 3%?
Proportion between 0.42 + 0.03 = 0.45 and 0.42 - 0.03 = 0.39, which is the p-value of Z when X = 0.45 subtracted by the p-value of Z when X = 0.39.
X = 0.45
\(Z = \frac{X - \mu}{\sigma}\)
By the Central Limit Theorem
\(Z = \frac{X - \mu}{s}\)
\(Z = \frac{0.45 - 0.42}{0.0235}\)
\(Z = 1.28\)
\(Z = 1.28\) has a p-value of 0.8997
X = 0.39
\(Z = \frac{X - \mu}{s}\)
\(Z = \frac{0.39 - 0.42}{0.0235}\)
\(Z = -1.28\)
\(Z = -1.28\) has a p-value of 0.1003
0.8997 - 0.1003 = 0.7994
0.7994 = 79.94% probability that the proportion of persons with myopia will differ from the population proportion by less than 3%.
Sammy had 250 points. On his next move, his score became 0.Which equation represents the situation? Explain.Equation 1250 - 250 = 0Equation 2250 + -250
Answers
We know that the initial state is 250 and the final state is 0.
Then, we can express the relation between this two states with a difference that shows the changes between this two states.
Because the score goes down by 250 points, we can write:
\(\begin{gathered} \text{Initial state}+\text{Variation}=\text{Final state} \\ 250+(-250)=0 \\ 250-250=0 \end{gathered}\)Answer: Equation 1, because it shows the initial and final scores and the variation between them.
FOR 58 POINTS!!!
Angle H is half as large as angle J. Angle J is one fourth as large as angle K. Angle K has a measure of 240 degrees. What is the measure of angle H?
Answers
Answer:
30
Step-by-step explanation:
A Set S with two or more vectors is linearly independent if and only if no vector in S is expressible as a linear combination of the other vectors in S
Prove this Statement/Theorem
Answers
Answer:
Step-by-step explanation:
To prove the statement "A Set S with two or more vectors is linearly independent if and only if no vector in S is expressible as a linear combination of the other vectors in S," we must show that both directions of the statement are true. That is, we must show that if a set S is linearly independent, then no vector in S is expressible as a linear combination of the other vectors in S, and conversely, if no vector in S is expressible as a linear combination of the other vectors in S, then the set S is linearly independent.
First, let's assume that the set S is linearly independent. This means that for any vectors v1, v2, ..., vn in S, the equation a1v1 + a2v2 + ... + anvn = 0 has only the trivial solution a1 = a2 = ... = an = 0. We will prove that no vector in S is expressible as a linear combination of the other vectors in S.
Suppose, for the sake of contradiction, that there exists a vector v in S that can be expressed as a linear combination of the other vectors in S. That is, there exist vectors v1, v2, ..., vn-1 in S such that v = b1v1 + b2v2 + ... + bn-1vn-1, where not all of the bi's are zero. Without loss of generality, assume that b1 is nonzero. Then we can write v1 as a linear combination of the other vectors in S:
v1 = (1/b1)v - (b2/b1)v2 - ... - (bn-1/b1)vn-1
Substituting this expression for v1 in the equation a1v1 + a2v2 + ... + anvn = 0, we get:
a1[(1/b1)v - (b2/b1)v2 - ... - (bn-1/b1)vn-1] + a2v2 + ... + anvn = 0
Multiplying both sides by b1 and rearranging, we get:
(a1/b1)v + (-a1b2/b1)v2 + ... + (-a1bn-1/b1)vn-1 + a2v2 + ... + anvn = 0
This is a linear combination of vectors in S that equals the zero vector, and not all of the coefficients are zero, since a1 is nonzero. But this contradicts the assumption that S is linearly independent, so our assumption that there exists a vector in S that can be expressed as a linear combination of the other vectors in S must be false. Therefore, no vector in S is expressible as a linear combination of the other vectors in S.
Now let's assume that no vector in S is expressible as a linear combination of the other vectors in S. We will prove that the set S is linearly independent. Suppose, for the sake of contradiction, that there exist vectors v1, v2, ..., vn in S such that the equation a1v1 + a2v2 + ... + anvn = 0 has a nontrivial solution, where not all of the ai's are zero. Without loss of generality, assume that a1 is nonzero. Then we can write v1 as a linear combination of the other vectors in S:
v1 = (-a2/a1)v2 - ... - (an/a1)vn
Substituting this expression for v1 in the equation a1v1 + a2v2 + ... + anvn = 0, we get:
0 = a1(-a2/a1)v2 + ... + a
You have to lend Rs. 75000 for two years for a purpose. If a
finance company A lends money at 10% per annum
compounded annually and finance company B lends money
at 8% per annum compounded semi-annuallly. From which
finance company will you take the loan and why? Give your
reason with calculation.
Answers
Answer:
The amount to be returned at Finance company B is less than that of Finance company A so it is profitable to take the loan from Finance company B.
Step-by-step explanation:
★ Finance company A :
A = 75,000 (1 + 0.1)²
A = 75,000 × 1.21
A = 90,750
★ Finance company B :
A = 75,000 (1 + 0.04)⁴
A = 75,000 × 1.16986
A = 87,739.5
If you invest this money $7,185.51 each month in an account that compounds monthly with an APR of 2.5%, how much will you have saved i) after 1 year? ii) after 3 years?
Answers
He would have saved $87,221.02 after 1 year
He would have saved $268,335.90 after 3 years
What is an ordinary annuity?
An ordinary annuity means a fixed amount invested at specific intervals, in this case, $7,185.51 is invested monthly, which means that its future value can be computed using the future value formula of an ordinary annuity as shown below:
FV=PMT*(1+r)^N-1/r
FV=future value of an ordinary annuity
PMT=monthly payment invested every month
r=monthly interest rate=annual interest/12
N=number of months that monthly payments were
FV after 1 year:
PMT=$7,185.51
r=monthly interest rate=2.5%/12=0.00208333333333333
N=number of months in 1 year=12
FV=$7,185.51*(1+0.00208333333333333)^12-1/0.00208333333333333
FV=$7,185.51*(1.00208333333333333)^12-1/0.00208333333333333
FV=$7,185.51*0.02528845698324970/0.00208333333333333
FV=$87,221.02
FV after 3 years:
PMT=$7,185.51
r=monthly interest rate=2.5%/12=0.00208333333333333
N=number of months in 3 years=36
FV=$7,185.51*(1+0.00208333333333333)^36-1/0.00208333333333333
FV=$268,335.90
Find out more about future value of an ordinary annuity on:brainly.com/question/24703884
#SPJ1
Joint probability of two statistical dependent events Y and Z can be written as P(Y and Z) =
Select one:
a. P(Y) * P(Z|Y) + P(Z)
b. P(Y) * P(Z|Y) - P(Z + Y)
c. P(Z + Y) * P(Y|Z)
d. P(Z - Y) * P(Y|Z)
e. P(Y) * P(Z|Y)
Note: Answer B is NOT the correct answer. Please find the correct answer. Any answer without justification will be rejected automatically.
Answers
The correct answer is option e. The joint probability of two statistical dependent events Y and Z can be written as P(Y and Z) = P(Y) * P(Z|Y).
The concept of joint probability is utilized in probability theory, a statistical tool that investigates the probability of two events happening simultaneously. It is an estimation of the probability of two or more events occurring simultaneously. Joint probability is a method of defining the probability of two events happening at the same time.The joint probability of two statistical dependent events Y and Z can be written as P(Y and Z) = P(Y) * P(Z|Y).This implies that the possibility of Z happening given Y has happened multiplied by the probability of Y happening is the joint probability of Y and Z. P(Z|Y) refers to the probability of Z occurring when Y is true or has already occurred. It is conditional probability and is often used to calculate joint probabilities.The formula for conditional probability is P(A|B) = P(A and B)/P(B), which can be simplified to P(A and B) = P(A|B) * P(B). This formula is applicable to P(Y and Z), where P(Y and Z) = P(Z|Y) * P(Y).
The correct answer is option e.
for more such question on probability
https://brainly.com/question/30390037
#SPJ8
hypothesis that there is a relationship between parents’ and children’s party identification. Would we be correct in inferring that such a relationship also exists in the population? Explain your answer. What is the probability that any relationship we found is due to pure chance?
Answers
Answer:
No
It could be purely due to chance.
Step-by-step explanation:
A population is defined as the whole group which has the same characteristics. For example a population of the college belongs to the same college . But a sample may be an element of a population.
So it is not necessary for a population to have the same characteristics as the sample.
But it is essential for the sample to have at least one same characteristics as the population.
So we would not be correct in inferring that such a relationship also exists in the population.
It is a hypothesis which can be true or false due to certain conditions or limitations as the case maybe.
For example in a population of smokers some may be in the habit of taking cocaine. But a sample of cocaine users does not mean the whole population uses it.
It could be purely due to chance if we find out that there is a relationship between parents’ and children’s party identification in the population.
The tee for the sixth hole on a golf course is 400 yards from the tee. On that hole, Marsha hooked her ball to the left, as sketched below. Find the distance between Marsha’s ball and the hole to the nearest tenth of a yard. Answer any time! :D
Answers
Answer:
181.8 yd
Step-by-step explanation:
The law of cosines is good for this. It tells you for triangle sides 'a' and 'b' and included angle C, the length of 'c' is given by ...
c^2 = a^2 +b^2 -2ab·cos(C)
For the given geometry, this is ...
c^2 = 400^2 +240^2 -2(400)(240)cos(16°) ≈ 33,037.75
c ≈ √33037.75 ≈ 181.8 . . . yards
Marsha's ball is about 181.8 yards from the hole.

Answer:
181.8 yds
Step-by-step explanation:
I got it correct on founders edtell
Identify the slope of the line using the 2 points
(8,-7), (6,17)
12
-12
12
12

Answers
Alexa is hooked on a new book series, The Galaxy. Each book in the series is the same length and chronicles a different year in the Waka Waka Galaxy. Alexa has cleared off the top shelf of her bookcase to leave room for each of the books as they come out. There is a proportional relationship between the number of books on the shelf, x, and how much shelf space the books take up (in inches), y.
The equation that models this relationship is y=2x.
How many books will take up 16 inches of shelf space? Write your answer as a whole number or decimal.

Answers
Answer: 8 books
Step-by-step explanation:
y= how much shelf space take up (inches)
x= # of books
y=2x
in this situation 16=y
16=2x
divide both sides by 2
8=x
Allie receives a $20 gift card for the local coffee shop, where she only buys lattes and muffins. If the price of a latte is $4 and the price of a muffin is $2, then we can conclude that Julia:
Answers
If the price of a latte is $4 and the price of a muffin is $2, then we can conclude that Julia can buy 5 lattes or 10 muffins ($20) if she chooses to buy only one of the two goods.
How to illustrate the price?A price is the sum of money that one party pays or receives in exchange for another's goods or services. The cost of production may go by another name in certain circumstances. If the item is a "good" in a commercial transaction, the cost of the item will probably be referred to as its "price."
In this case, Allie receives a $20 gift card for the local coffee shop, where she only buys lattes and muffins. Here, we can conclude that Julia can buy 5 lattes. This will be 5 × $4 = $20 or 10 muffins which will be:
= 10 × $2
= $20
Learn more about price on:
https://brainly.com/question/1153322
#SPJ1
Simplify the following expression.
(6m5g5) 2
Answers
The simplified exponential expression in the context of this problem is given as follows:
\((6m^5g^5)^2 = 32m^{10}g^{10}\)
How to simplify the exponential expression?The exponential expression in the context of the problem is defined as follows:
\((6m^5g^5)^2\)
The power of a power rule is used when a single base is elevated to multiple exponents, and states that simplified expression is obtained keeping the base, while the exponents are multiplied.
Applying the exponent of 2, we have that:
6² = 36.5 x 2 = 10.Hence the simplified exponential expression in the context of this problem is given as follows:
\((6m^5g^5)^2 = 32m^{10}g^{10}\)
More can be learned about the power of a power property at brainly.com/question/11975096
#SPJ1