Derek and Eric share £30 in the ratio 2:3. How much does Eric get?
Answers
\( \quad \qquad\huge \underline{\boxed{\sf Answer}}\)
Let's assume the ratio constants in terms of x ~
that is ;
\( \sf2x\)and
\( \sf3x\)Now, according to question ~
\( \qquad \sf \dashrightarrow \: 2x + 3x = 30\)
\(\qquad \sf \dashrightarrow \: 5x = 30\)
\(\qquad \sf \dashrightarrow \: x = 30 \div 5\)
\(\qquad \sf \dashrightarrow \: x = 6\)
So, Derek gets :
\(\qquad \sf \dashrightarrow \: 2x = 2 \times 6 = £12\)
And Eric gets :
\(\qquad \sf \dashrightarrow \: 3x = 3 \times 6 =£ 18\)
Related Questions
The price of an item has risen to $258 today. Yesterday it was $120. Find the percentage increase
Answers
Answer
138
Step-by-step explanation:
The answer is 138 because, when you take 258 and subtract it by 120, you will end up with 138!
Answer:
It was most likely raised by 46%
Step-by-step explanation:
120/258
Which of the following statements is an opinion?
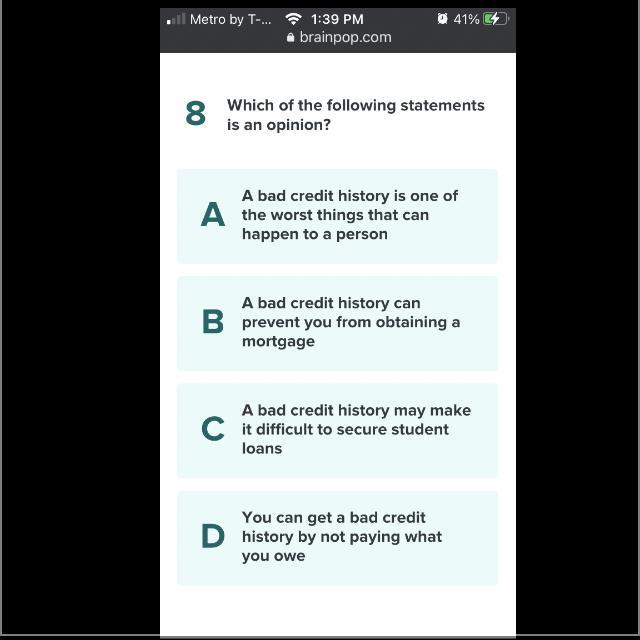
Answers
Question 10
Solve for b.
b³ = 8
Enter your answer in the box.

Answers
Answer:
\({ \sf{ {b}^{3} = 8}} \: \: \\ { \sf{ {b}^{3} = {2}^{3} }} \\ { \sf{ {(b}^{3}) {}^{ \frac{1}{3} } = {( {2}^{ 3}) }^{ \frac{1}{3} } }} \\ { \sf{b ={ \boxed{ 2}}}}\)
Answer:
b=2
Step-by-step explanation:
\(b^{3} = 8\\\\b^{3} = 2^{3} \\\\b=+2\)
You are given the great circle of a sphere is a length of 25 miles. What is the volume of the sphere
Answers
The volume of the sphere is approximately 3431.82 cubic miles.
To find the volume of a sphere, we need the radius of the sphere. The length of a great circle is the circumference of the sphere, which is related to the radius by the formula C = 2πr, where C is the circumference and r is the radius.
In this case, we are given that the length of the great circle is 60 miles. We can use this information to find the radius of the sphere.
C = 2πr
60 = 2πr
Divide both sides of the equation by 2π:
r = 60 / (2π)
r = 30 / π
Now that we have the radius, we can use the formula for the volume of a sphere:
V = (4/3)πr³
V = (4/3)π(30/π)³
V = (4/3)π(27000/π³)
V = (4/3)π(27000/π³)
V = (4/3)π(27000/π³)
V = (4/3)(27000/π²)
V = (4/3)(27000/9.87) (approximating π to 3.14)
V ≈ 3431.82 cubic miles
Therefore, the volume of the sphere is approximately 3431.82 cubic miles.
for such more question on volume
https://brainly.com/question/6204273
#SPJ8
Question
You are given the great circle of a sphere is a length of 60 miles. What is the volume of the sphere?
Write a function for the sinusoid (the curve).
У
(2,5)
14
(1, -1)
3
1
Choose...
3 cos x + 2
The function is f(x) = 3 sin x
3 sin x
3 cos x
2 X

Answers
The equation of the sinusoid function is:
3 Sin πx + 2.
Let's analyze the given options to find the correct equation:
a. 3 Cos πx + 2:
This option is a cosine function with a vertical shift of 2, but it does not have the correct amplitude or period. Therefore, it is not the correct equation.
b. 3 Sin x: This option is a sine function with the correct amplitude, but it does not have the correct vertical shift or period. Therefore, it is not the correct equation.
c. 3 Sin πx + 2: This option is a sine function with the correct amplitude and vertical shift. Let's check if it has the correct period:
To determine if the period is correct, we need to calculate the x-values when the function repeats itself.
In this case, we need to find x-values such that sin(πx) = 0, since the function will reach its maximum and minimum points again at those x-values.
sin(πx) = 0 when πx = 0, π, 2π, 3π, ...
Solving for x, we have:
πx = 0 ⟹ x = 0
πx = π ⟹ x = 1
πx = 2π ⟹ x = 2
πx = 3π ⟹ x = 3
From this, we can see that the function repeats itself every integer value of x, which matches the given information.
Therefore, option (c) is the correct equation: 3 Sin πx + 2.
Option (d) 3 Cos x does not have the correct vertical shift or period, so it is not the correct equation.
Hence, the equation of the sinusoid function is:
3 Sin πx + 2.
Learn more about sinusoid function click;
https://brainly.com/question/21008165
#SPJ1
Solve: 2m³-5m² - 7m = 0
Answers
Answer:
m = - 1 , m = 0 , m = \(\frac{7}{2}\)
Step-by-step explanation:
2m³ - 5m² - 7m = 0 ← factor out common factor m from each term
m(2m² - 5m - 7) = 0
factorise the quadratic 2m² - 5m - 7
consider the factors of the product of the coefficient of the m² term and the constant term which sum to give the coefficient of the m- term
product = 2 × - 7 = - 14 and sum = - 5
the factors are + 2 and - 7
use these factors to split the m- term
2m² + 2m - 7m - 7 ( factor the first/second and third/fourth terms )
2m(m + 1) - 7(m + 1) ← factor out (m + 1) from each term
(m + 1)(2m - 7)
then
2m³ - 5m² - 7m = 0
m(m + 1)(2m - 7) = 0 ← in factored form
equate each factor to zero and solve for m
m = 0
m + 1 = 0 ( subtract 1 from both sides )
m = - 1
2m - 7 = 0 ( add 7 to both sides )
2m = 7 ( divide both sides by 2 )
m = \(\frac{7}{2}\)
solutions are m = - 1 , m = 0 , m = \(\frac{7}{2}\)
7a/9bc divided by 21a/12b
Answers
Answer:
Step-by-step explanation:
I dont know if you meant to punch in a c into the equation but if you didnt mean to i have both answers
The one that contains a c in the fraction that you asked for!

In order to pass your final assessment you must answer 75% of the questions correctly.There are 84 questions then I must get how many questions correct to pass
Answers
Answer:
63 answers
Hope this helps :p
The total number of questions to be answered correctly so that 75% of answers are correct is 63.
∵ To pass the assessment, the percentage of questions to be answered correctly = 75.
That means, for every 100 questions, the number of correct answers required = 75
∴ For 1 question, the number of correct answers required= 75/100
=3/4
But, the total number of questions in the assessment = 84
∴ For 84 questions, the number of correct answers required = 3/4×84
= 63
Hence, the total number of questions to be answered correctly so that 75% of answers are correct is 63.
For more questions on percentage,
https://brainly.com/question/24877689
https://brainly.com/question/843074
1. The gragh below shows indifference curves (IC₁ and IC2) and budget constraints (BC₁, BC₂, BC) for All who enjoys consuming tacos with soda. (6 points) a. Based on the Budget Constraint BC2, if Ali's budget is $28 then what would be the the prices of soda and/or taco? b. What combination of tacos and soda quantities optimizes Ali's utility? Tacos 0 1 (2,3) 2 3 (4,3) BC3 IC1 BC2 6 7 8 IC 2 9 BC1 10 Cans of Soda
Answers
I cannot interpret or analyze visual graphs. However, I can provide some general guidance on how to approach the questions:
a. To determine the prices of soda and/or taco based on the Budget Constraint BC2, you need to find the points where the budget line BC2 intersects with the axes (taco and soda quantities). The prices can be derived from the slope of the budget line, where the slope represents the rate at which one good can be traded for another.
b. To find the combination of taco and soda quantities that optimizes Ali's utility, you need to look for the point where the indifference curve (IC) is tangent to the budget line (BC). This point represents the maximum level of utility Ali can achieve within his budget constraint. It's the point where the marginal rate of substitution (MRS) between tacos and soda is equal to the price ratio of tacos to soda.
Which transformation reflects f(x)=(x-1)² over the y-axis?
A) f'(x) = 0.3((x-1)²+1)
B) f'(x) = -3((x-1)²+1)
C) f'(x) = (-4x-1)²+1
D) f'(x) = (0.1x-1)²+1
Answers
Answer:
A) f'(x) = 0.3((x-1)²+1)
Step-by-step explanation:
Dana has driven her car 95,598 miles. She estimates she can
drive the car another 5000 miles before the mileage reaches
100,000 miles. Use the rules for estimating differences to
explain if Dana is correct.
Answers
Answer: Dana estimation is incorrect because difference = 598 miles
Step-by-step explanation:
Given data,
Dana has driven her car 95,598 miles.
She estimates she can
drive the car another 5000 miles.
she can,
drive the car another 5000 miles before the mileage reaches
100,000 miles.
Estimated Mileage of the car is equal to 100,000 miles.
That is,
Estimated Mileage of the car is = 100,000 miles.
So,
We can write,
Total distance Dana has to travel = already driven + additional miles to cover
Total distance Dana has to travel = 95,598 + 5,000 miles
Total distance Dana has to travel = 1,00,598 miles.
As per mileage of car is 100,000 miles.
So, Dana has to travel = 1,00,598 miles.
So, Dana estimation is incorrect because difference is = 100,598 - 100,000
Therefore,
Dana estimation is incorrect because difference = 598 miles
Learn more about event correlation here: brainly.com/question/17152677
#SPJ9
When Terell started high school, 2,314 students attended his school. On the day of his graduation, only 1,512 students attended his school. The number of students who attended terrel school decreased by ____________%
Answers
Answer:
minus the total students with the one that attained on the graduation day & the answer/total high school students ×100
thats it the answer is the __%
All six digits in the number are even one digit is used twice all other digits are used once the ones digit is 4 times the hundreds digit the tens digit id the difference of the ones digit and hundreds digit the same digit is in the tens place and hundreds thousands place the thousands digit is not zero
Answers
Answer:
rffrefr
Step-by-step explanation:
Help please!!!! 25 POINTS
A football is kicked into the air. Its path can be expressed using the equation:
h = -5t2 + 20.5t + 2 where h represents height in feet and t represents time in
seconds:

Answers
a) The initial height of the football at t = 0 is 2 feet.
b) The ball reaches its maximum height at approximately t = 2.05 seconds.
c) The maximum height of the ball is approximately 23.9 feet.
d) It takes approximately 4.579 seconds for the ball to hit the ground.
a) The initial height of the football at time t = 0 can be found by substituting t = 0 into the equation \(5t^2 + 20.5t + 2:h = -5(0)^2 + 20.5(0) + 2 = 0 + 0 + 2 = 2\)
Therefore, the initial height of the football is 2 feet.
b) To find the time at which the ball reaches its maximum height, we can observe the graph of the equation h = \(-5t^2 + 20.5t + 2.\) The maximum height corresponds to the vertex of the parabolic graph. The t-coordinate of the vertex can be calculated using the formula t = -b/2a, where a and b are the coefficients of the quadratic equation.
In this case, a = -5 and b = 20.5. Plugging these values into the formula, we get:
\(t = -20.5 / (2\times (-5)) = -20.5 / -10 = 2.05\)
Therefore, the ball reaches its maximum height at approximately t = 2.05 seconds.
c) The maximum height of the ball can be found by substituting the time t = 2.05 into the equation \(h = -5t^2 + 20.5t + 2:\)
h = -5(2.05)^2 + 20.5(2.05) + 2 ≈ -20.125 + 42.025 + 2 ≈ 23.9
Therefore, the maximum height of the ball is approximately 23.9 feet.
d) To find the time it takes for the ball to hit the ground, we need to determine when the height h becomes zero. We can set the equation \(-5t^2 + 20.5t + 2 = 0\) and solve for t.
This quadratic equation can be solved using factoring, the quadratic formula, or by graphing. The solutions are t ≈ -0.179 and t ≈ 4.579. Since time cannot be negative in this context, the ball takes approximately 4.579 seconds to hit the ground.
For more such questions on maximum height
https://brainly.com/question/26746473
#SPJ8
Recall that with base-ten blocks: 1 long 10 units, 1 flat 10 longs, and 1 block 10 flats. What is the fewest number of multibase blocks that can be used to represent the corresponding numeral in the given base?
a. 20 longs in base seven
b. 10 longs in base three
Answers
a. The answer is: The fewest number of multibase blocks required to represent 20 longs in base seven is 2 flats.
b. The answer is: The fewest number of multibase blocks required to represent 10 longs in base three is 3 flats and 1 unit.
a. To represent 20 longs in base seven, we need to find the fewest number of multibase blocks required.
In base seven, we have the following conversions:
1 long = 1 unit
1 flat = 10 units
1 block = 10 flats
To represent 20 longs, we can use 2 flats (each flat representing 10 units) and 0 units since there are no remaining units.
So, the fewest number of multibase blocks required would be 2 flats.
Therefore, the answer is: The fewest number of multibase blocks required to represent 20 longs in base seven is 2 flats.
b. To represent 10 longs in base three, we need to find the fewest number of multibase blocks required.
In base three, we have the following conversions:
1 long = 1 unit
1 flat = 3 units
1 block = 3 flats
To represent 10 longs, we can use 3 flats (each flat representing 3 units) and 1 unit since there is one remaining unit.
So, the fewest number of multibase blocks required would be 3 flats and 1 unit.
Therefore, the answer is: The fewest number of multibase blocks required to represent 10 longs in base three is 3 flats and 1 unit.
for such more question on fewest number
https://brainly.com/question/859564
#SPJ8
Jeremy wants to give a 20% gratuity to his cab driver. His fare is $35.50. What is the total amount he will pay the driver?
Answers
Answer:
$42.60.
Step-by-step explanation:
You multiply 35.50 by .20 (that's decimal version of 20%) which equals 7.10. Then you add 35.50+7.10=42.60
ASAP! GIVING BRAINLIEST! Please read the question THEN answer correctly! No guessing.

Answers
Answer:
C. \(F(x) = -x^2 - 3\)
Step-by-step explanation:
The function, F(x), has flipped over the x-axis (as seen) meaning that the function has to have a negative sign in front. The function has also shifted downwards 3 units, meaning that 3 has to have been subtracted from the function.
This makes "C," the correct answer, as it fulfills these requirements.
f(x) = x + 5 and g(x) = 4x + 3, find f(g(x))
Answers
Answer:
4x+8
Step-by-step explanation:
f(x)=x+5
g(x)=4x+3
Now,
f(4x+3)
4x+3+5
4x+8
Mean, Median, Mode, Appropriate Measures, Standard
Deviation
Use this data set to answer all questions on this page.
513, 490, 496, 380, 490, 513, 503, 513, 500, 492
Question 1 Which of the following would be APPROPRIATE measure(s) of center. (1)Mean (2)Median (3) Mode. Question 2 Find the standard deviation. Round your answer to the tenths place(one decimal place)
Answers
Answer:
Question 1: The appropriate measures of center for this data set would be (1) Mean and (2) Median. There is no mode in this data set as there are no repeating values.
Question 2: To find the standard deviation, we first need to find the mean:
Mean = (513 + 490 + 496 + 380 + 490 + 513 + 503 + 513 + 500 + 492) / 10 = 494.0
Next, we find the difference between each data point and the mean:
(513 - 494.0), (490 - 494.0), (496 - 494.0), (380 - 494.0), (490 - 494.0), (513 - 494.0), (503 - 494.0), (513 - 494.0), (500 - 494.0), (492 - 494.0)
19, -4, 2, -114, -4, 19, 9, 19, 6, -2
Then we square each difference:
361, 16, 4, 12996, 16, 361, 81, 361, 36, 4
The sum of these squared differences is:
361 + 16 + 4 + 12996 + 16 + 361 + 81 + 361 + 36 + 4 = 14136
To find the variance, we divide the sum of squared differences by the number of data points minus one:
Variance = 14136 / 9 = 1570.7
Finally, we find the standard deviation by taking the square root of the variance:
Standard deviation = √1570.7 ≈ 39.6 (rounded to the tenths place)
Step-by-step explanation:
Twelve cards are numbered from 1 to 12 and placed in a box. One card is selected at random and not replaced. Another is randomly selected. What is the probability of selecting two even numbers?
Answers
In this case, we are to determine the probability of selecting two even numbers. This can be solved as follows:There are six even numbers: {2, 4, 6, 8, 10, 12}.We can use the concept of conditional probability since the first event affects the probability of the second event. This can be expressed as follows:
In this case, P(A) represents the probability of selecting an even number, and P(B|A) represents the probability of selecting an even number given that the first card selected was even. P(A) = 6/12 = 1/2 (there are six even numbers and twelve cards in total)P(B|A) = 5/11 (there are five even numbers left in the box after the first even number is selected, and eleven cards are left in total).
The probability of selecting two even numbers can be found by multiplying these probabilities: P(A) x P(B|A) = (1/2) x (5/11) = 5/22Therefore, the probability of selecting two even numbers is 5/22.Answer: 5/22
For more questions on: probability
https://brainly.com/question/23417919
#SPJ8
The results of a test that follows a normal distribution have a mean value of 10.0 and a standard deviation of 1.
Find the probability that a single reading is between 8 and 10
Answers
Answer:
The value is \(P(8 < X < 10 ) = 0.8186\)
Step-by-step explanation:
From the question we are told that
The mean is \(\mu = 10 .0\)
The standard deviation is \(\sigma = 1\)
Generally the probability that a single reading is between 8 and 10 is mathematically represented as
\(P(8 < X < 10 ) = P( \frac{8 - 10 }{ 1} < \frac{X - \mu }{ \sigma } < \frac{10 - 10 }{1} )\)
\(\frac{X -\mu}{\sigma } = Z (The \ standardized \ value\ of \ X )\)
=> \(P(8 < X < 10 ) = P( -2 < Z< 1 )\)
=> \(P(8 < X < 10 ) = P( Z< 1 ) - P( Z < -2 )\)
From the z table the area under the normal curve to the left corresponding to 1 and -2 is
\(P( Z< 1 ) = 0.84134\)
and
\(P( Z < -2 ) = 0.02275\)
=> \(P(8 < X < 10 ) = 0.84134 - 0.02275\)
=> \(P(8 < X < 10 ) = 0.8186\)
which term applies to numbers that cannot be written in this form
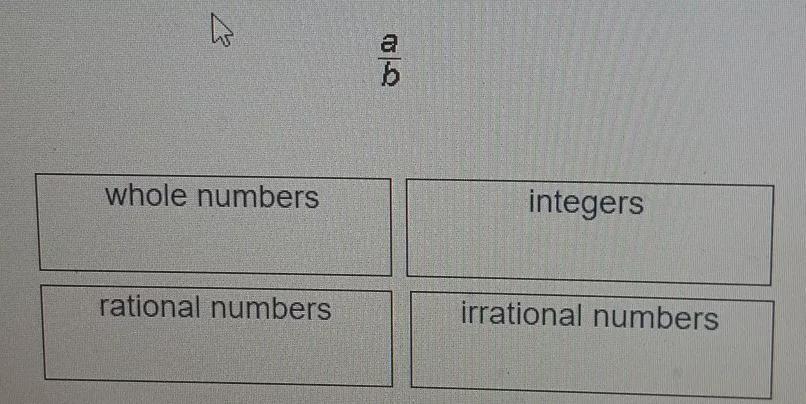
Answers
Answer:
Irrational Numbers.
Explanation:
If a number can be written in the form:
\(\frac{a}{b},b\neq0\)Such a number is said to be Rational.
Thus, any number that cannot be written in this form is called an Irrational Number.
The measure of one small angles of a right triangle is 45 less than twice the measure of the other small angle. Find the measure of both angles
Answers
Answer:
x + x - 45 = 90
2x - 45 = 90
2x = 135
x = 67.5, so x - 45 = 22.5
The other two angles measure 22.5° and 67.5°.
1 The area of the circle is 641 cm². What is the radius of the circle in cm? A=64 R=? Note: The figure is not drawn to scale A) 8 B 9 6 D) 5
Answers
Step 1: Let's recall the formula of the area of a circle, as follows:
\(\text{Area = }\pi\ast r^2,\text{ where r is the radius of the circle}\)Step 2: Let's replace the values we know in the formula above:
\(64\text{ }=\text{ 3.14 }\ast r^2\text{ }\Rightarrow\text{ r = }\sqrt{\frac{64}{3.14\text{ }}}=4.515\text{ centimetres}\)In case the area of the circle is 641, instead of 64:
\(641\text{ = 3.14 }\ast r^2\text{ }\Rightarrow\text{ }\sqrt{\frac{641\text{ }}{3.14\text{ }}\text{ = 14.288 centimetres}}\)None of the choices given is correct, unless 4.515 is rounded to 5.
The length of a rectangle is 8 feet longer than the width and the perimeter is 132 feet. What it the width of the rectangle?
Answers
Answer: the width is 29 feet and the length is 37
Step-by-step explanation:
Identify the graph of the inequality 2(2x-1)+7< 13 or -2x+5-10.

Answers
From the resulting solution, the correct linear inequality graph is Graph C.
Solving inequality expressionGiven the inequality equation below:
2(2x-1)+7< 13 or -2x+5 ≤ -10.
Simplify the expression
2(2x-1)+7< 13
Expand
4x - 2 + 7 < 13
4x + 5 < 13
4x < 13 - 5
4x < 8
x < 2
For the inequality -2x+5 ≤ -10.
-2x+5 ≤ -10
-2x ≤ -15
x ≥ 7.5
Hence the solution to the given system of inequalities are x < 2 and x ≥ 7.5
Learn more on inequality graph here: https://brainly.com/question/24372553
#SPJ1
A rectangle has a length of (x + 4) feet and a width of (x + 7) feet. The expression
2(x+)+2(x + 7) represents the perimeter of the rectangle.
Which expression also represents the perimeter of the rectangle, in feet?
A (x + 4) + (x + 4) + (x + 7) + (x + 7) W
B (x + 4)(x + 4)(x + 7)(x + 7)
C 4x + 11
D 22x

Answers
Answer:
A
Step-by-step explanation:
No need. It’s simple.
B can’t be it because it uses multiplication.
C can’t be it because it makes no sense.
D also makes no sense.
answer the question submitted

Answers
The function g(x) = 4x² - 28x + 49 can be rewritten as g(x) = 4(x - 7/2)² - 147 after completing the square.
To complete the square for the function g(x) = 4x² - 28x + 49, we follow these steps:
Step 1: Divide the coefficient of x by 2 and square the result.
(Coefficient of x) / 2 = -28/2 = -14
(-14)² = 196
Step 2: Add and subtract the value obtained in Step 1 inside the parentheses.
g(x) = 4x² - 28x + 49
= 4x² - 28x + 196 - 196 + 49
Step 3: Rearrange the terms and factor the perfect square trinomial.
g(x) = (4x² - 28x + 196) - 196 + 49
= 4(x² - 7x + 49) - 147
= 4(x² - 7x + 49) - 147
Step 4: Write the perfect square trinomial as the square of a binomial.
g(x) = 4(x - 7/2)² - 147
Therefore, the function g(x) = 4x² - 28x + 49 can be rewritten as g(x) = 4(x - 7/2)² - 147 after completing the square.
For more such questions square,click on
https://brainly.com/question/27307830
#SPJ8
The probable question may be:
Rewrite the function by completing the square.
g(x)=4x²-28x +49
g(x)= ____ (x+___ )²+____.
Which equation, when solved, glves 8 for the value of x?
5
7
3
3
OA. 2x+ź= 4x+14
OB. 1-9=34-12
OC 41-2=15-4
OD. *-7= x+14
Reset
Ne

Answers
Answer:
C.
Step-by-step explanation:
5/4x-2=3/2x-4
5/4x-3/2x = -4+2
(multiply both sides by 4)
5x-6x=-16+8
-x=-8
(multiply by -1)
x=8
Answer:
C
Step-by-step explanation:
\(\frac{5x}{2} +\frac{7}{2} =\frac{3x}{4} +14\\) isolate the terms with the variable x
\(\frac{5x}{2} -\frac{3x}{4} =14-\frac{7}{2}\) get the same denominator and combine like terms
\(\frac{10x-3x}{4} = \frac{28-7}{2}\) solve
\(\frac{7x}{4} =\frac{21}{2}\) crossmultiply and solve for x
\(x=\frac{4*21}{7*2} =6\) so is not the first option
try second
\(\frac{5x}{4} -9=\frac{3x}{2} -12\) same steps as before
\(\frac{5x-6x}{4}=9-12\\)
\(\frac{-x}{4} =\frac{-3}{1}\) so x=12 not the second option
try third option
\(\frac{5x}{4} -2=\frac{3x}{2} -4\)
\(\frac{5x-6x}{4} =2-4\)
\(\frac{-x}{4} =\frac{-2}{1}\) so x=8
Chalk is an ionic compound. Which is a property of all ionic compounds that makes chalk particularly useful for writing on a chalkboard? A a high melting point B hardness and brittleness C inability to dissolve in water D a multicolored appearance
Answers
The correct answer is B. Hardness and brittleness
Explanation:
The ions in materials such as chalk and other ionic compounds are bonded by electrostatic forces. These features give ionic compound unique characteristics. This includes the fact these materials are usually hard, which means they do not deform easily and the fact these are brittle, which means they break easily.
These properties can be observed in chalk because the chalk itself keeps its shape or does not deform (hardness) but it breaks easily under pressure (brittleness), indeed due to this last property it is possible to write using chalk and due to the first property it is possible the chalk is a durable material.
Answer:
B.
Step-by-step explanation: