Cual es el complemento de 32 grados? :c
Answers
Answer:
El complemento de 32 grados es 58 grados.
Related Questions
the product of 13 and the sum of a number an 15
Answers
Answer:
(15+x) · 13
Step-by-step explanation:
plz mark brainliest!
Find all values f x that make the equation true: 4/x+4=x-2/x
Answers
Step-by-step explanation:
4/x + 4 = x - 2/x
multiply everything by x
4 + 4x = x² - 2
x² - 4x - 6 = 0
the general solution to such a quadratic equation
ax² + bx + c = 0
is
x = (-b ± sqrt(b² - 4ac))/(2a)
in our case
x = (4 ± sqrt((-4)² - 4×1×-6))/(2×1) =
= (4 ± sqrt(16 + 24))/2 = (4 ± sqrt(40))/2 =
= (4 ± sqrt(4×10))/2 = (4 ± 2×sqrt(10))/2 =
= 2 ± sqrt(10)
x1 = 2 + sqrt(10) = 5.16227766...
x2 = 2 - sqrt(10) = -1.16227766...
Un profesor de Enseñanza Básica le indica a sus alumnos que escojan tres dígitos
diferentes del conjunto {1, 2, 3, 4, 5} y formen números mixtos colocando los dígitos
en el casillero . También les recuerda que la parte fraccionaria tiene que ser
menor que 1, por ejemplo
2
3
5
. ¿Cuál es la diferencia entre el mayor y el menor de los
números mixtos que se pueden formar?
Answers
Enseñanza Básica is the term used to describe the first level of education in the Chilean education system, which includes the first to eighth grades. A teacher of Enseñanza Básica asked his students to choose three-digit mixed numbers that can be formed.
A mixed number is a number that has both a whole number and a fraction component. To form three-digit mixed numbers, we need to have a whole number that is less than 100 and a proper fraction that has a denominator less than or equal to 99. Here are some examples:123 4/567 2/8109 1/2382 3/47There are a total of 900 three-digit numbers that can be formed using digits 1 to 9 without repetition. To find the number of three-digit mixed numbers that can be formed, we need to count the number of ways we can choose a proper fraction with a denominator less than or equal to 99. There are 99 possible denominators, and for each denominator, there are 98 possible numerators (excluding 0 and the denominator itself). Therefore, the total number of three-digit mixed numbers that can be formed is:900 x 99 x 98 = 8,334,600There are 8,334,600 three-digit mixed numbers that can be formed using digits 1 to 9 without repetition.For such more question on fraction
https://brainly.com/question/78672
#SPJ8
The difference between the greatest and the least mixed numbers is 9.87 - 6.0789 ≈ 3.7911.
How to solveThe three digits different from {1, 2, 3, 4, 5} can be chosen from {0, 6, 7, 8, 9}.
The greatest mixed number is formed by placing the largest digit as the whole number and the remaining two digits as the fraction in descending order, i.e., 9 87/100 or 9.87.
The smallest mixed number is formed by placing the smallest non-zero digit as the whole number and the remaining two digits as the fraction in ascending order, i.e., 6 07/90 or 6.0789.
The difference between the greatest and the least mixed numbers is 9.87 - 6.0789 ≈ 3.7911.
Read more about algebra here:
https://brainly.com/question/4344214
#SPJ1
The Question in English
A Basic Education teacher tells his students to choose three digits
different from the set {1, 2, 3, 4, 5} and form mixed numbers by placing the digits
in the locker It also reminds them that the fractional part has to be
less than 1, for example
2
3
5
. What is the difference between the greatest and the least of the
mixed numbers that can be formed?
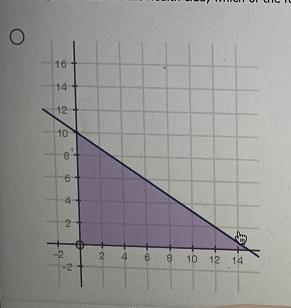
11. (05.05 MC)A family of 3 children and 2 adults visited a health club. The club charges sy an hour for each child and $x an hour for each adult. If the family does not want to spend morethan $30 an hour at the health club, which of the following graphs best models the situation? (5 points)161412108624610 1214
Answers
Given f(1) = 8 and
f(n) = 3 f(n-1) - 2 then f (4) =
Answers
Answer:
190
Step-by-step explanation:
f(1)=8
f(2)=3f((2-1))-2, f(2)=22
f(3)=3f((3-1))-2, f(3)=64
f(4)=3f((4-1))-2, f(4)=190
By which rule are these triangles congruent?

Answers
Answer:
sss
Step-by-step explanation:
Question 2 of 39
Look at this series: 56, 54, 50, 38, 34, ... What number should come next?
A) 23
B) 18
C) 20
D) 32
E) 26
Answers
Answer:
D) 32
Step-by-step explanation:
Given;
series: 56, 54, 50, 38, 34, ....
find the difference between successive numbers;
56 54 50 38 34 x
2 4 12 4 2
The highest difference between the numbers is 12, after which it decreases to 4 and finally back 2.
The next number "x" is calculated as;
34 - 2 = x
34 - 2 = x
32 = x
Therefore, the next number should be 32.
The next number that should come next in the series is 32.
Sequence is an arrangement of two or more things in a successive order. Series is the cumulative sum of a given sequence of terms.
Given the numbers in the series: 56, 54, 50, 38, 34, . . ..
The difference is 2, 4, 12, 4, 2
The highest difference between the numbers is 12, after which it decreases to 4 and finally back 2. Hence:
The next number = 34 - 2 = 32
The next number that should come next in the series is 32.
Find out more on series at: https://brainly.com/question/13171394
The function y = 2.5x + 3 can be used to determine the cost in dollars for a taxi ride of x miles.
What is the rate of change of the cost in dollars with respect to the number of miles?
$5.50/mile
$1/mile
$3/mile
$2.50/mile
Answers
Answer:
C. $2.50
Step-by-step explanation:
x=1 y=5.5
x=2 y=2.5
Bob dio cuatro quintos de sus lapices a barbara, luego dio dos tercios de los lapices restantes a bonnie, si termino con 10 lapices para el... ¿ cuantos lapices tenia bob al principio?
Answers
Bob had 50 pencils in the beginning.
How is a fractional number expressed?A fractional number is expressed in the form -
x/y {where y ≠ 0)
Given is that Bob gave four - fifths of his pencils to Barbara, then he gave two - thirds of the remaining pencils to bonnie.
Assume that he had {x} pencils in the beginning. We can write -
4x/5 + 2/3(x - 4x/5) = 10
4x/5 + 2x/3 - 8x/15 = 10
x(4/5 + 2/3 - 8/15) = 10
x = 10/0.93
x = 50
Therefore, Bob had 50 pencils in the beginning.
To solve more questions on Archimedes principle , visit the link below -
https://brainly.com/question/787619
#SPJ9
{QUESTION IN ENGLISH -
Bob gave four fifths of his pencils to Barbara, then he gave two thirds of the remaining pencils to bonnie, if he ended up with 10 pencils for himself... how many pencils did bob have at the beginning?}
By the fourth day of a particular week, 3 items have already sold. What is the probability that there will be less than a total of 5 items sold during that week
Answers
The probability that less than five items will be sold from the items during the week will be 0.67.
How to calculate probabilityFrom the complete question, the number of items that were sold in a week was given in a distribution table.
From the table, the probability that there will be less than a total of 5 items sold during that week will be:
= P(3 or 4 items sold) / P(3 or more items sold)
= (0.15 + 0.05) / (0.15 + 0.05 + 0.05 + 0.05)
= 0.20/0.30
= 0.67
In conclusion, the probability is 0.67.
Learn more about probability on:
https://brainly.com/question/25870256
What is the simplest form of 1.764?
0 21
0 42
0 3²(7²)
22(32)(74)
please explain why because I don’t want someone to guess this is kinda important, ty
Answers
Answer:
\(1764 = 2^2 \times 3^2 \times 7^2\)
Step-by-step explanation:
Divide by the prime numbers in increasing order until you find all the prime factors.
The first few prime numbers are: 2, 3, 5, 7, 11, 13, 17
1764/2 = 882
882/2 = 441
441/3 = 147
147/3 = 49
49/7 = 7
7/7 = 1
\(1764 = 2^2 \times 3^2 \times 7^2\)
paula bought an electric drill at 75% of the regular price.She paid 32.90 for the drill. What was the regular price?(round to the nearest cent)
Answers
Answer:
$43.87.
Step-by-step explanation:
let the regular price be x, then
0.75x = 32.9
x = 32.9 / 0.75 = $43.87
Answer:
43.87
Step-by-step explanation:
Let the regular price be T
T x 75% = 32.903T/4 = 32.903T = 4 x 32.903T = 131.60T = 43.87I need help with this question.. :')

Answers
The equation of the line passing through A and B is y = (4/5)x - (2/5).
What is the line example's equation?A straight line's general equation is y = mx + c, where m is the gradient and y = c is the value at which the line intersects the y-axis. The y-axis intercept is denoted by the number c. A straight line with gradient m and intercept c on the y-axis has the equation y = mx + c.
The point-slope form of a linear equation can be used to find the equation of the line passing through points A and B:
y - y1 = m(x - x1) (x - x1)
where m denotes the slope of the line, (x1, y1) denotes the coordinates of point A or B, and (x, y) denotes the coordinates of any other point on the line.
To calculate the slope, we can use points A (3, 2) and B (8, 6).
m = (y2 - y1) / (x2 - x1) = (6 - 2) / (8 - 3)\s= 4 / 5
So the equation for the line connecting A and B is:
y - 2 = (4/5)(x - 3) (x - 3)
This equation can be simplified by multiplying both sides by 5:
5y - 10 = 4x - 12
Then we can rearrange it to form the slope-intercept equation, y = mx + b:
5y = 4x - 2
y = (4/5)x - (2/5)
As a result, the equation for the line connecting A and B is y = (4/5)x - (2/5).
To know more about Equation of Line visit:
https://brainly.com/question/21511618
#SPJ1
What is the meaning of "∈-minimal element"?

Answers
The term "∈-minimal element" typically refers to an element within a set that satisfies a specific condition related to set membership.
More specifically, an element x is considered an "∈-minimal element" if there is no other element y in the same set such that y ∈ x, where "∈" represents set membership. In other words, x is the smallest element within the group in terms of the membership relation.
This concept is often used in the context of partially ordered sets or posts, where elements are related to each other by a partial order relation. An "∈-minimal element" is the smallest element within the group based on the given partial order relation defined on the set.
Learn more about the axiom of regularity here:
https://brainly.com/question/32269173
#SPJ1
Find ordered pairs y=-7x+8
Answers
The ordered pairs for the equation y = -7x + 8 are (0, 8), (1, 1), and (-1, 15).
What are the ordered pairs for the equation y?To find ordered pairs for the equation y = -7x + 8, we can substitute different values of x and solve for y.
Let's choose three values of x:
When x = 0, y = -7(0) + 8 = 8. So one ordered pair is (0, 8).
When x = 1, y = -7(1) + 8 = 1. So another ordered pair is (1, 1).
When x = -1, y = -7(-1) + 8 = 15. So another ordered pair is (-1, 15).
Therefore, the ordered pairs are (0, 8), (1, 1), and (-1, 15).
Learn more about ordered pairs for the equation here:https://brainly.com/question/2055583
#SPJ1
A student asks 18 friends to participate in a psychology experiment.
A Convenience
B) Random
Systematic
D Cluster
E) Stratified
Answers
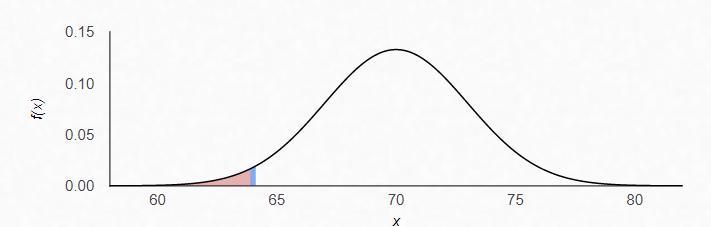
Suppose the mean height for adult males in the U.S. is about 70 inches and the standard deviation is about 3 inches. Assume men’s heights follow a normal curve.
a) (2 pts) What percentage of adult males are under 64 inches tall? Use the 68-95-99.7 and draw a picture that illustrates your rationale.
b) (2 pts) What percentage of adult males are between 64 and 73 inches tall? Use the 68-95-99.7 and draw a picture that illustrates your rationale.
Answers
Using the Empirical Rule, it is found that:
a) 2.5% of adult males are under 64 inches tall.
b) 81.5% of adult males are between 64 and 73 inches tall.
What does the Empirical Rule state?It states that, for a normally distributed random variable, approximately:
68% of the values in the distribution are within 1 standard deviation of the mean.95% of the values in the distribution are within 2 standard deviations of the mean.99.7% of the values in the distribution are within 3 standard deviations of the mean.For item a, we have that 64 is two standard deviations below the mean, hence, considering the symmetry of the normal distribution:
2.5% of adult males are under 64 inches tall.
As shown by the first graph at the end of the answer.
For item b, we have that 64 is two standard deviations below the mean, while 73 is one above, hence, considering the symmetry of the normal distribution:
P = 0.5 x 95 + 0.5 x 68 = 81.5%.
As shown by the two blue sections, plus the left brown section, in the second graph.
More can be learned about the Empirical Rule at https://brainly.com/question/20875827
#SPJ1

pls help me giving brainless.

Answers
Answer:
five and three ninths
six and seven tenths
nine and one fifth
Two numbers total 51 and have a difference of 23. Find the two numbers?
Answers
Answer:
14 and 37
I just kept checking all the pairs I could think of until I got to this answer.
3 of the 12 bows that Janice has are red. What percent of the bows are not red?
Answers
Answer: 75%
Hope this helps answer your question!
Answer:
75%
Step-by-step explanation:
3 of 12 bows are red, meaning that 9 bows are not red. (12-3 = 9)
9 non-red bows/12 bows total = 3/4 = 0.75 = 75%
Please help some one and if you could explain please

Answers
Answer:
t = 1 second
Step-by-step explanation:
initial height = 16
penny to hit the ground = 0
0 = -16t^2 + 16
-16 = -16t^2 ÷
-16 ÷ -16 = -16t^2 ÷ -16
1 = t^2
√1 = √t^2
1 = t
Consider the polynomial
(4mn^2n - 2mn + 6) + (6mn^2 - 1) - (mn^2 - 2 + 9mn)
Combine all like terms and enter the coefficients for each term into the blanks below

Answers
(4mn^2n - 2mn + 6) + (6mn^2 - 1) - (mn^2 - 2 + 9mn)
First, let's remove the parentheses:
4mn^2 - 2mn + 6 + 6mn^2 - 1 - mn^2 + 2 - 9mn
Next, let's combine like terms by adding or subtracting coefficients of the same variables:
(4mn^2 + 6mn^2 - mn^2) + (-2mn - 9mn) + (6 + 2 - 1)
Simplifying further:
9mn^2 - 11mn + 7
So, the coefficients for each term are:
9, -11, 7
Heeeelp please, Can be zero or not?
with all steps and explanay.

Answers
The value of integral is 3.
Let's evaluate the integral over the positive half of the interval:
∫[0 to π] (cos(x) / √(4 + 3sin(x))) dx
Let u = 4 + 3sin(x), then du = 3cos(x) dx.
Substituting these expressions into the integral, we have:
∫[0 to π] (cos(x) / sqrt(4 + 3sin(x))) dx = ∫[0 to π] (1 / (3√u)) du
Using the power rule of integration, the integral becomes:
∫[0 to π] (1 / (3√u)) du = (2/3) . 2√u ∣[0 to π]
Evaluating the definite integral at the limits of integration:
(2/3)2√u ∣[0 to π] = (2/3) 2(√(4 + 3sin(π)) - √(4 + 3sin(0)))
(2/3) x 2(√(4) - √(4)) = (2/3) x 2(2 - 2) = (2/3) x 2(0) = 0
So, the value of integral is
= 3-0
= 3
Learn more about Definite integral here:
https://brainly.com/question/30760284
#SPJ1
Answer:
\(3-\displaystyle \int^{\pi}_{-\pi} \dfrac{\cos x}{\sqrt{4+3 \sin x}}\; \text{d}x\approx 0.806\; \sf (3\;d.p.)\)
Step-by-step explanation:
First, compute the indefinite integral:
\(\displaystyle \int \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x\)
To evaluate the indefinite integral, use the method of substitution.
\(\textsf{Let} \;\;u = 4 + 3 \sin x\)
Find du/dx and rewrite it so that dx is on its own:
\(\dfrac{\text{d}u}{\text{d}x}=3 \cos x \implies \text{d}x=\dfrac{1}{3 \cos x}\; \text{d}u\)
Rewrite the original integral in terms of u and du, and evaluate:
\(\begin{aligned}\displaystyle \int \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&=\int \dfrac{\cos x}{\sqrt{u}}\cdot \dfrac{1}{3 \cos x}\; \text{d}u\\\\&=\int \dfrac{1}{3\sqrt{u}}\; \text{d}u\\\\&=\int\dfrac{1}{3}u^{-\frac{1}{2}}\; \text{d}u\\\\&=\dfrac{1}{-\frac{1}{2}+1} \cdot \dfrac{1}{3}u^{-\frac{1}{2}+1}+C\\\\&=\dfrac{2}{3}\sqrt{u}+C\end{aligned}\)
Substitute back u = 4 + 3 sin x:
\(= \dfrac{2}{3}\sqrt{4+3\sin x}+C\)
Therefore:
\(\displaystyle \int \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x= \dfrac{2}{3}\sqrt{4+3\sin x}+C\)
To evaluate the definite integral, we must first determine any intervals within the given interval -π ≤ x ≤ π where the curve lies below the x-axis. This is because when we integrate a function that lies below the x-axis, it will give a negative area value.
Find the x-intercepts by setting the function to zero and solving for x in the given interval -π ≤ x ≤ π.
\(\begin{aligned}\dfrac{\cos x}{\sqrt{4+3\sin x}}&=0\\\\\cos x&=0\\\\x&=\arccos0\\\\\implies x&=-\dfrac{\pi }{2}, \dfrac{\pi }{2}\end{aligned}\)
Therefore, the curve of the function is:
Below the x-axis between -π and -π/2.Above the x-axis between -π/2 and π/2.Below the x-axis between π/2 and π.So to calculate the total area, we need to calculate the positive and negative areas separately and then add them together, remembering that if you integrate a function to find an area that lies below the x-axis, it will give a negative value.
Integrate the function between -π and -π/2.
As the area is below the x-axis, we need to negate the integral so that the resulting area is positive:
\(\begin{aligned}A_1=-\displaystyle \int^{-\frac{\pi}{2}}_{-\pi} \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&=- \left[\dfrac{2}{3}\sqrt{4+3\sin x}\right]^{-\frac{\pi}{2}}_{-\pi}\\\\&=-\dfrac{2}{3}\sqrt{4+3 \sin \left(-\frac{\pi}{2}\right)}+\dfrac{2}{3}\sqrt{4+3 \sin \left(-\pi\right)}\\\\&=-\dfrac{2}{3}\sqrt{4+3 (-1)}+\dfrac{2}{3}\sqrt{4+3 (0)}\\\\&=-\dfrac{2}{3}+\dfrac{4}{3}\\\\&=\dfrac{2}{3}\end{aligned}\)
Integrate the function between -π/2 and π/2:
\(\begin{aligned}A_2=\displaystyle \int^{\frac{\pi}{2}}_{-\frac{\pi}{2}} \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&= \left[\dfrac{2}{3}\sqrt{4+3\sin x}\right]^{\frac{\pi}{2}}_{-\frac{\pi}{2}}\\\\&=\dfrac{2}{3}\sqrt{4+3 \sin \left(\frac{\pi}{2}\right)}-\dfrac{2}{3}\sqrt{4+3 \sin \left(-\frac{\pi}{2}\right)}\\\\&=\dfrac{2}{3}\sqrt{4+3 (1)}-\dfrac{2}{3}\sqrt{4+3 (-1)}\\\\&=\dfrac{2\sqrt{7}}{3}-\dfrac{2}{3}\\\\&=\dfrac{2\sqrt{7}-2}{3}\end{aligned}\)
Integrate the function between π/2 and π.
As the area is below the x-axis, we need to negate the integral so that the resulting area is positive:
\(\begin{aligned}A_3=-\displaystyle \int^{\pi}_{\frac{\pi}{2}} \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&= -\left[\dfrac{2}{3}\sqrt{4+3\sin x}\right]^{\pi}_{\frac{\pi}{2}}\\\\&=-\dfrac{2}{3}\sqrt{4+3 \sin \left(\pi\right)}+\dfrac{2}{3}\sqrt{4+3 \sin \left(\frac{\pi}{2}\right)}\\\\&=-\dfrac{2}{3}\sqrt{4+3 (0)}+\dfrac{2}{3}\sqrt{4+3 (1)}\\\\&=-\dfrac{4}{3}+\dfrac{2\sqrt{7}}{3}\\\\&=\dfrac{2\sqrt{7}-4}{3}\end{aligned}\)
To evaluate the definite integral, sum A₁, A₂ and A₃:
\(\begin{aligned}\displaystyle \int^{\pi}_{-\pi} \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&=\dfrac{2}{3}+\dfrac{2\sqrt{7}-2}{3}+\dfrac{2\sqrt{7}-4}{3}\\\\&=\dfrac{2+2\sqrt{7}-2+2\sqrt{7}-4}{3}\\\\&=\dfrac{4\sqrt{7}-4}{3}\\\\ &\approx2.194\; \sf (3\;d.p.)\end{aligned}\)
Now we have evaluated the definite integral, we can subtract it from 3 to evaluate the given expression:
\(\begin{aligned}3-\displaystyle \int^{\pi}_{-\pi} \dfrac{\cos x}{\sqrt{4+3 \sin x}}\; \text{d}x&=3-\dfrac{4\sqrt{7}-4}{3}\\\\&=\dfrac{9}{3}-\dfrac{4\sqrt{7}-4}{3}\\\\&=\dfrac{9-(4\sqrt{7}-4)}{3}\\\\&=\dfrac{13-4\sqrt{7}}{3}\\\\&\approx 0.806\; \sf (3\;d.p.)\end{aligned}\)
Therefore, the given expression cannot be zero.

Find the length of RS is S is between R and T, the length of RS is the length of RT,
RS= 3x-3, and ST = 2x + 6.

Answers
Answer:
RS = 6 units
Step-by-step explanation:
You want the length of segment RS when it is 1/3 of the length of RT and the lengths are given by the expressions RS=3x-3 and ST=2x+6.
SetupUsing the given expressions, we can write an equation for segment RS.
RS = 1/3(RS +ST)
3x -3 = 1/3((3x -3) +(2x +6))
SolutionMultiplying by 3 and simplifying, we get ...
9x -9 = 5x +3
4x = 12
x = 3
RS = 3x -3 = 3·3 -3 = 6
The length of RS is 6 units.
__
Additional comment
The length of ST is 2(3) +6 = 12, and the length of RT is 6+12 = 18.
1. Mr. Santos teaches 120 students. Sixty percent of his students earned an
'A' on the final exam. How many students earned an 'A' on the final exam?
Answers
Answer:
72 students
Step-by-step explanation:
Answer:
72
Step-by-step explanation:
because if you multiply 120 by 60% also 0.6, then you will get 72.
a plane covered a distance of 630 miles in 6 hours . for the first part of the trip the average speed was 100 mph and for the second part of the tripvthe average speed was 110cmph.what is the time it flew at each speed?
Answers
We know that the plane flew at each speed which is at 100mph and 110mph for 3 hours each.
What is speed?Speed is what it means. The rate at which the location of an object shifts in any direction.
Speed is defined as the ratio of the distance traveled to the time required to cover that distance.
Speed is a scalar quantity since it just has a direction and no magnitude.
The distance an object covers in a given amount of time is known as
speed.
The SI unit of speed is m/s or meters per second.
It has a scalar value.
Speed=Distance/Time.
So, using the speed:
Total miles = 630 in 6 hours.
Then,
100*3=300
110*3=330
Now,
300 + 330 = 630 miles
Therefore, we know that the plane flew at each speed which is at 100mph and 110mph for 3 hours each.
Know more about speed here:
https://brainly.com/question/13943409
#SPJ1
What is the equation through the points: (-7, -3), (1, 2)
ASAP please
Answers
The equation of the line passing through the points (-7, -3) and (1, 2) is \(y = \frac{5}{8}x + \frac{11}{8}\).
What is the equation of the line?The formula for equation of line is expressed as;
y = mx + b
Where m is slope and b is y-intercept.
First, we determine the slope of the line.
Given the two points are (-7, -3) and (1, 2)
We can find the slope of the line by using the slope formula:
m = ( y₂ - y₁ ) / ( x₂ - x₁ )
Substituting the values, we get:
m = (2 - (-3)) / (1 - (-7))
m = 5/8
Using the point-slope form, plug in one of the given points and slope m = 5/8 to find the equation of the line.
Let's use the point (-7, -3:
y - y₁ = m(x - x₁)
\(y - (-3) = \frac{5}{8}( x - (-7) ) \\\\y + 3 = \frac{5}{8}(x + 7 )\\\\y + 3 = \frac{5}{8}x + \frac{35}{8} \\ \\y = \frac{5}{8}x + \frac{35}{8} - 3\\\\y = \frac{5}{8}x + \frac{11}{8}\)
Therefore, the equation of the line is \(y = \frac{5}{8}x + \frac{11}{8}\).
Learn more about equation of line here: brainly.com/question/2564656
#SPJ1
Please help I’m stuck and keep getting the wrong answer

Answers
The time spent higher than 26 meters above the ground is 0.42 minutes. Answer: 0.42
A Ferris wheel is 30 meters in diameter and boarded from a platform that is 4 meters above the ground.
The six o'clock position on the Ferris wheel is level with the loading platform.
The wheel completes 1 full revolution in 2 minutes.
We have to find how many minutes of the ride are spent higher than 26 meters above the ground.
So, let's start with some given data,Consider the height of a person at the six o'clock position = 4 meters
So, the height of a person at the highest point = 4 + 15 = 19 meters (since the diameter is 30 meters, the radius will be 15 meters)
Also, the height of a person at the lowest point = 4 - 15 = -11 meters
Therefore, the Ferris wheel completes one cycle from the lowest point to the highest point and back to the lowest point.
So, the total distance travelled will be = 19 + 11 = 30 meters.
Also, we are given that the wheel completes 1 full revolution in 2 minutes.
We need to calculate the time spent higher than 26 meters above the ground.
So, the angle between the 6 o'clock position and 2 o'clock position will be equal to the angle between the 6 o'clock position and the highest point.
This angle can be calculated as follows:
Angle = Distance travelled by the Ferris wheel / Circumference of the Ferris wheel * 360 degrees
Angle = 30 / (pi * 30) * 360 degrees
Angle = 360 degrees / pi
= 114.59 degrees
So, the total angle between the 6 o'clock position and the highest point is 114.59 degrees.
Now, we need to find out how much time is spent at an angle greater than 114.59 degrees.
This can be calculated as follows:
Time = (Angle greater than 114.59 degrees / Total angle of the Ferris wheel) * Total time taken
Time = (180 - 114.59) / 360 * 2 minutes
Time = 0.42 minutes
For more related questions on time spent:
https://brainly.com/question/28263820
#SPJ8
Simplify the exponential expression. 2^4⋅3^4
Answers
Answer:
1296
Step-by-step explanation:
2^4⋅3^4
= 16 * 81
= 1296
The graph of a function is f(x)=3√x.
Based on this, find:
a) F(0,75), F(9), F(7).
b) the value of x with F(x) = 3;6;7.
Answers
Answer:
F(0.75)= 3/2 sq. root 3
F(9)= 9
F(7)= 3 sq. root 7
b) x= +-1
x=+-4
x= +- 49/9