Craig wants to use an elevator to carry identical packages having the same weight. Each package weighs 4 pounds and Craig weighs 90 pounds. If the elevator can carry a maximum of 330 pounds at a time, which inequality shows the maximum number of packages, n, that Craig can carry with himself in the elevator if he is the only passenger?
Answers
Answer:
90+4n less than or equal to 330
Step-by-step explanation:
since craig weighs 90 pounds. he will be a constant weight
Since each package weighs 4 pounds, the variable will be 4n
The elevator can hold a maximum of 330 pounds so that is what the inequality should have on the other side
the final equation will be:
90+4n less than or equal to 330
Related Questions
Create and solve
an equation with
2 variables(x).
Answers
Answer:
5x-2=3x+4
x=3
Step-by-step explanation:
Hope I helped!
What is the value of x in the figure shown below?
С
Ε
4.2.
4.2
A
co
36
56
4
4.
B
D

Answers
In 1990, there were 4,500 deaths due to lung diseases in miners aged 20 to 64 years. The expected number of deaths in this occupational group, based on age-specific deaths rates from lung diseases in all males aged 20 to 64 years, was 1,800 during 1990. What is the standardized mortality ratio (SMR) for lung disease in miners
Answers
Answer:
2.5
Step-by-step explanation:
We have that the standardized mortality ratio (SMR) is the relationship between the number of deaths observed in a year, that is, those that occurred and the number of expected deaths, that is, those that were predicted.
SMR = observed / expected
therefore if we replace we have:
SMR = 4500/1800
SMR = 2.5
Which means that the standardized mortality ratio (SMR) is 2.5
2. A(n) is NOT an example of an agreement. (1 point)
O lease
O month-to-month
O annual
O fine print
Answers
An Annual is not an example of an agreement.
Can the following list represent a complete probability model? P(2)= 1/12 P(3) = 2/3 P(4) = 1/4
Answers
Therefore , the solution of the given problem of probability comes out to be a complete probability model cannot be represented by this list.
What exactly is probability?The main objective of each considerations technique is to calculate the likelihood that a claim is true or that a particular incident will occur. Anything between 0 and 1, were 0 traditionally denotes a percentage and 1 typically denotes the degree of certainty, can be used to represent chance. A probability illustration shows the likelihood that a particular event will occur.
Here,
The probabilities assigned to the outcomes do not add up to 1, hence the following list cannot be a complete probability model.
=> P(2) + P(3) + P(4)
=> 1/12 + 2/3 + 1/4
=> (1 + 8 + 3) / 12
=> 12 / 12 = 1
In a complete probability model, the total of the probabilities should always be equal to 1, indicating that there is a probability of 1 that one of the events will occur.
In this instance, there is a missing probability since the sum of the probabilities assigned to the possible possibilities is less than 1.
Therefore, a complete probability model cannot be represented by this list.
To know more about probability visit:
https://brainly.com/question/11234923
#SPJ1
A hat contains 35 marbles. Of them, 20 are red and 15 are green. If one marble is randomly selected out of this hat, what is the probability that this marble is red? Round your answer to two decimal places. P(A) =
Answers
Answer:
P(A) = 0.57 (rounded to two decimal places).
Step-by-step explanation:
The probability of selecting a red marble from the hat can be found by dividing the number of red marbles by the total number of marbles:
P(red) = number of red marbles / total number of marbles
P(red) = 20/35
We can simplify this fraction by dividing both the numerator and denominator by 5:
P(red) = 4/7
So the probability of selecting a red marble from the hat is 4/7, or approximately 0.57 when rounded to two decimal places.
Therefore, P(A) = 0.57 (rounded to two decimal places).
what decimal is equivalent to 41 over 100 (pls keep it simple i am only in 5th grade )
Answers
Answer: 0.41
Step-by-step explanation:
To find the decimal point of a fraction, divide the numerator (the top half of the fraction) by the denominator (the bottom half of the fraction).
41 over 100 as a decimal point would be 41 divided by 100
Which produces the equivalent decimal, 0.41
P.S this is also how you find the percent of a number. To get the percent, move the decimal point 2 digits over (0.41 to 41.) and then add the percentage sign to the end of the number (41%)
0.41 = 41%
so 41 over 100 is 0.41, and 41 is also 41% of 100 (per cent means per 100)
Best of luck in 5th grade :)
Mary’s trapezoid-shaped garden has a perimeter of 24 yd. She knows the length of three of the sides, 3 yd, 6 yd, and 9 yd.
What is the length of the fourth side?
Choose...
Answers
Answer:
6
Step-by-step explanation:
to find the perimeter of a trapezoid you add all the sides together
therefore we do it backwards
24-3-6-9=6
Solution :-
We know that perimeter is the sum of all sides, and here we have been provided with perimeter and the length of three sides. Now, we can assume the length of other side as any variable, say x. And develop a linear equation, and solve it. Thus,
A/Q,
→ 3yd + 6yd + 9yd + x = 24yd
→ 18yd + x = 24yd
→ x = 24yd - 18yd
→ x = 6yd
Thus, the length of the fourth side is 6yd.
Hope that helps :)
Determine if each proportion on the left is True or False. Answer options on the right side may be used more than once.
True
False
28/16=14/8
3/5=9/15
4/32=10/78
3/4=12/16
Answers
Answer:
28/16=14/8 true
3/5=9/15 true
4/32=10/78 false
3/4=12/16 true
Step-by-step explanation:
DID IT ON BRIDGE
What is the measure of arc PSR? *
75 degrees
260 degrees
65
100

Answers
Answer:
it most likely would be 260 degrees
Count the best-case number of + operations performed by the following pseudocode segment. Assume that all possible data sets are equally likely. Preconditions: X = {x1, x2, x3, x4, x5} ⊆ {10, 20, 30, 40, 50, 60, 70, 80}, where x1 < x2 < x3 < x4 < x5. t ← 0 i ← 1 while t < 101 do t ← t + xi i ← i + 1
Answers
For the best cases there will be 6+operations, The number of operations are best cases 6 and the worst cases are 10.
Given that,
The following pseudocode snippet performs the maximum number of + operations. Assume that the probability of each potential piece of data is equal. Preconditions: X = {x₁, x₂, x₃, x₄, x₅} ⊆ {10, 20, 30, 40, 50, 60, 70, 80}, where x1 < x2 < x3 < x4 < x5. t ← 0 i ← 1 while t < 101 do t ← t + xi i ← i + 1
We know that,
Here,
X = {x₁, x₂, x₃, x₄, x₅} ⊆ {10, 20, 30, 40, 50, 60, 70, 80}
By doing the iteration method
Iteration process till 4th iteration we get 6
Therefore, For the best cases there will be 6+operations, The number of operations are best cases 6 and the worst cases are 10.
To learn more about number visit: https://brainly.com/question/17429689
#SPJ4
Can you please help me
Answers
Therefore the measure of angle 1 is 36°
Estimate the sum of 379+409=
Answers
Answer:
Round both numbers to 1 significant figure.
400+400=800
800 is the answer.
Solve.
4 There are 42 tubes of oil paint on trays. Each tray
holds 6 tubes. How many trays of tubes are there?
Show your work.
7
Answers
Answer: 7
Step-by-step explanation:
Since there are 42 tubes and each tray can hold 6 tubes, it will be 42/6 which is 7.
What is B^2+8b+7??
Can someone explain it step by step please?
Answers
Step-by-step explanation:
B^2+8b+7 is a quadratic expression. It can be factored as (b+7)(b+1).
To factor a quadratic expression, you can use the following steps:
1. Find two numbers that add up to the coefficient of the middle term (8) and multiply to the constant term (7).
2. Write the quadratic expression as a product of two binomials, with the two numbers you found in step 1 as the coefficients of the terms in each binomial.
In this case, the two numbers that add up to 8 and multiply to 7 are 7 and 1. So, we can factor B^2+8b+7 as follows:
(b+7)(b+1)
This means that B^2+8b+7 is equal to the product of (b+7) and (b+1).
Here is a step-by-step explanation of how to factor B^2+8b+7:
1. The coefficient of the middle term is 8.
2. The constant term is 7.
3. The two numbers that add up to 8 and multiply to 7 are 7 and 1.
4. Therefore, B^2+8b+7 can be factored as (b+7)(b+1).
To solve it, you can use the quadratic formula, which is:
x = (-b ± √(b^2 - 4ac)) / 2a
In this case, a = 1, b = 8, and c = 7.
So, substituting the values, we get:
x = (-8 ± √(8^2 - 4(1)(7))) / 2(1)
x = (-8 ± √(64 - 28)) / 2
x = (-8 ± √36) / 2
x = (-8 ± 6) / 2
x = -1 or -7
Therefore, B^2+8b+7 is equal to -1 or -7.
PLEASE ANSWER QUICK, ITS URGENT!

Answers
Step-by-step explanation:
which part of the question do you need
Steve has 12 biscuits in a tin.
There are 7 digestive and 5 chocolate biscuits.
Steve takes two biscuits at random from the tin.
Work out the probability that he chooses two different types of biscuits.
Answers
For a certain triangle ABC, if a line intersects AC at D, intersects AB at E, and is parallel to CB, would the proportion AE | AD = EB | DC be accurate? Explain your answer.
Answers
The given proportion of triangle ABC as AE/AD = EB/DC is; Not Accurate
Understanding Basic proportionality theorem(Thale's Theorem)This theorem states that If a line is drawn parallel to one side of a triangle, then it cuts other two sides proportionally.
Thus, In ΔABC, DE || BC
By Thales theorem, we can say that;
AD/DB = AE/EC
Rearranging we can arrive at;
AE/AD = EC/DB
When we simplify further by adding 1 to both sides, we will get;
AD/AB = AE/AC
Thus, the given proportion is not accurate
Read more about Basic Proportionality Theorem at; https://brainly.com/question/14417137
The perimeter of an ICU ward, that is rectangular in shape, is 258 feet. The width is 37 feet less than the length. Find the dimensions of this ward.
Answers
Answer:
The answer is 9546
258*37=9546
What is the IQR for 10, 14, 15, 15, 16, 18, 19, 21
Answers
Answer:
15-18
Step-by-step explanation:
The IQR is the middle 50% of a set of numbers
There are 8 numbers, so its the middle 4
The middle 4 consists of 15,15,16,18
The range is 15-18
simplify a(x + y) - a(x - y)
Answers
Answer:
2ay
Step-by-step explanation:
To simplify first we expand the brackets.
ax+ay- (ax-ay)
Now collect like-terms
ax-ax= 0
ay- (-ay) = 2ay
Therefore The simplified version would be 2ay
Assume that a sample is used to estimate a population proportion p. Find the 99% confidence interval for a sample of size 315 with 37% successes. Enter your answer as an open-interval (i.e., parentheses) using decimals (not percents) accurate to three decimal places.
Answers
Answer:
The 99% confidence interval is = 0.37 +/- 0.070
= (0.300, 0.440)
Step-by-step explanation:
Confidence interval can be defined as a range of values so defined that there is a specified probability that the value of a parameter lies within it.
The confidence interval of a statistical data can be written as.
p+/-z√(p(1-p)/n)
Given that;
Proportion p = 37% = 0.37
Number of samples n = 315
Confidence interval = 99%
z value(at 99% confidence) = 2.58
Substituting the values we have;
0.37 +/- 2.58√(0.37(1-0.37)/315)
0.37 +/- 2.58√(0.00074)
0.37 +/- 2.58(0.027202941017)
0.37 +/- 0.070183587825
0.37 +/- 0.070
= (0.300, 0.440)
The 99% confidence interval is = 0.37 +/- 0.070
= (0.300, 0.440)
The managers at Smith's BBQ have been asked to cut back Total Wages by 2.5% in the next two
weeks to account for slow sales. Using the Current Week as the benchmark, what would be the
estimate for the reduced Total Wages for the next two weeks combined?
Answers
The required estimate for the reduced Total Wages for the next two weeks combined would be approximately 1.95 times the amount of money being paid to all employees over the course of a week in the Current Week.
What is the percentage?The percentage is the ratio of the composition of matter to the overall composition of matter multiplied by 100.
Here,
To estimate the reduced Total Wages for the next two weeks combined, we can use the following formula:
Reduced Total Wages = Current Total Wages x (1 - Wage Reduction Percentage)
Reduced Total Wages = C × (1 - 0.025) × 2
Simplifying this expression, we get:
Reduced Total Wages = C × 0.975 × 2
Reduced Total Wages = 1.95C
Therefore, the estimate for the reduced Total Wages for the next two weeks combined would be approximately 1.95 times the amount of money being paid to all employees over the course of a week in the Current Week.
Learn more about percentages here:
brainly.com/question/13450942
#SPJ1
1. The first quartile (1) of the ages of the 256 employees of CCNHS – Main Campus is 39 years old. What does it imply?
Answers
If the first quartile is 39 years old, it means that approximately one-fourth of the employees at CCNHS – Main Campus are 39 years old or younger.
The first quartile (Q1) of the ages of the 256 employees of CCNHS – Main Campus being 39 years old implies that 25% of the employees have an age equal to or less than 39 years old.
In statistical terms, the first quartile represents the point below which 25% of the data falls. It divides the data set into four equal parts, with each part containing 25% of the data. Therefore, if the first quartile is 39 years old, it means that approximately one-fourth of the employees at CCNHS – Main Campus are 39 years old or younger.
This information provides insight into the age distribution of the employees at the institution. It indicates that a significant portion of the employees are relatively young, with a quarter of them falling below the age of 39. Understanding the age demographics of the workforce can be useful for various purposes, such as planning professional development programs or implementing age-specific policies.
For more questions on quartile
https://brainly.com/question/28169373
#SPJ8
Pamela had $17. She bought 7 burgers for $5.50 and 2 kilograms of orange for $5.30. Find the remaining amount she has now.
$4.20
$5
$6
$6.20
Answers
Answer:
$ 6.20 Cents
Step-by-step explanation:
17 - 5.50= 11.5
11.50 - 5.30= 6.2
Add A Zero at the end
You Get 6.20
Question down below please look thank you
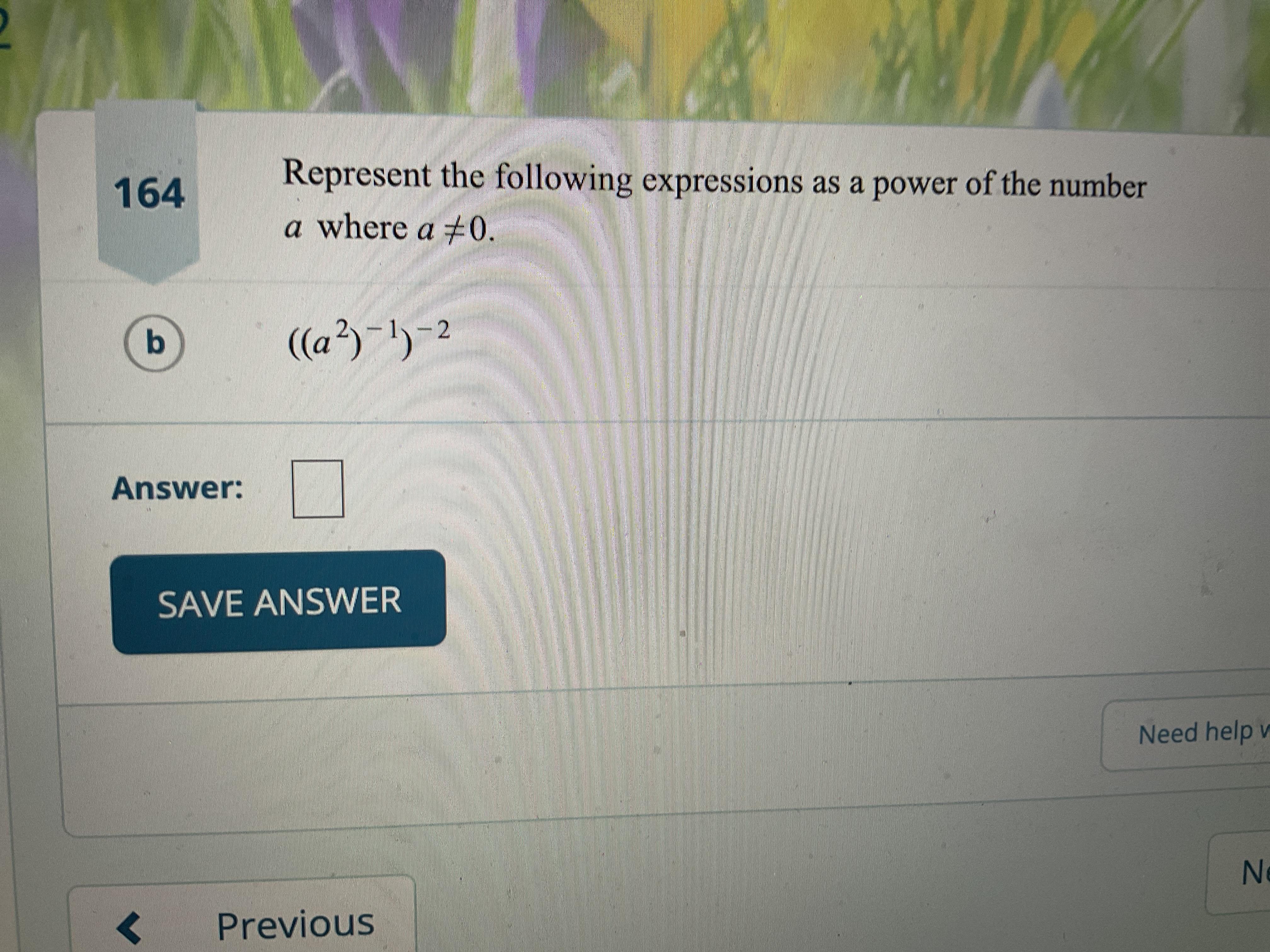
Answers
Applying the power rule, \(((a^2)^{-1})^{-2}\) expressed as the power of the number a is: \(a^4\).
What is the Power of a Power Rule?The power of a power rule of the laws of exponents states that, if we have an equation where one power is boosted by another power, we would simply keep the base constant, while we multiply the powers together in the given equation.
For example, \((x^m)^n = x^{mn}\).
Given the expression, where a ≠ 0:
\(((a^2)^{-1})^{-2}\)
Apply the power of power rule to express as the power of the number a.
To do this, multiply the powers, 2, -1, and -2 all together. we would have 4. Therefore, the expression is simplified as:
\(((a^2)^{-1})^{-2} = a^{(2 \times -1 \times -2)} = a^4\)
Learn more about the power of power rule on:
https://brainly.com/question/819893
#SPJ1
Find that the radius of curvature of ^2y=x^3-a^3
at the point where the
curves cut the X-axis.
Answers
The radius of curvature of the curve \(a^{2y\)=x³-a³ at the point where the curve intersects the x-axis is 27\(a^{\frac{3}{2}\).
To find the radius of curvature of the curve \(a^{2y\)=x³-a³ at the point where the curve intersects the x-axis, we need to first find the equation of the curve and then determine the value of y and its derivative at that point.
When the curve intersects the x-axis, y=0. Therefore, we have:
a⁰ = x³ - a³
x³ = a³
x = a
Next, we need to find the derivative of y with respect to x:
dy/dx = -2x/(3a²√(x³-a³))
At the point where x=a and y=0, we have:
dy/dx = -2a/(3a²√(a³-a³)) = 0
Therefore, the radius of curvature is given by:
R = (1/|d²y/dx²|) = (1/|d/dx(dy/dx)|)
To find d/dx(dy/dx), we need to differentiate the expression for dy/dx with respect to x:
d/dx(dy/dx) = -2/(3a²(x³-a³\()^{\frac{3}{2}\)) + 4x²/(9a⁴(x³-a³\()^{\frac{1}{2}\))
At x=a, we have:
d/dx(dy/dx) = -2/(3a²(a³-a³\()^{\frac{3}{2}\)) + 4a²/(9a⁴(a³-a³\()^{\frac{1}{2}\)) = -2/27a³
Therefore, the radius of curvature is:
R = (1/|-2/27a³|) = 27\(a^{\frac{3}{2}\)
To learn more about radius of curvature click on,
https://brainly.com/question/31403088
#SPJ1
A marketing consulting group wants to see whether placing a seasonal cookie product on an end cap (the shelf at the end of an aisle at a store) will make a difference in sales. The average sales of the seasonal cookie for this region was 650 units. A sample of 36 stores that placed the cookie on an end cap showed a sample mean of 671 units sold with a standard deviation of 81. The resulting p-value is 0.1288; thus, the null hypothesis is not rejected. The marketing consulting group concludes that placing the cookies on an end cap does not affect sales. What type of error is possible in this situation
Answers
Answer:
Type II error.
Step-by-step explanation:
We have a hypothesis test for the claim that placing a seasonal cookie product on an end cap (the shelf at the end of an aisle at a store) will make a difference in sales.
The null hypothesis will state that there is no difference, while the alternative hypothesis will state that there is significant positive difference.
The result is a P-value of 0.1288 and the null hypothesis failing to be rejected.
As the null hypothesis failed to be rejected, if an error has been made in the conclusion, is that we erroneusly accept a false null hypothesis.
This is a Type II error, where the null hypothesis is accepted although the alternative hypothesis is true.
Let f(x) = 6x^2 - 4x + 2. Find a constant c between 1 and 9 such that the average value of the function f(x) on the interval (1,9] is equal to fc).
A. 4.8735
B. 5.5402
C. 5.5721
D. -4.8735
E. 164
Answers
The value of constant c between 1 and 9 such that the average value of the function f(x) on the interval [1,9] is equal to is 5.
What is mean value theorem?Mean value theorem is the theorem which is used to find the behavior of a function.
The function given as,
\(f(x) = 6x^2 - 4x + 2\)
The value of function at 0,
\(f(0) = 6(0)^2 - 4(0) + 2\\f(0)=2\)
Differentiate the given equation,
\(f(x)' = 6\times2x - 4\times1 + 0\\f(x)' = 12x - 4\\f(x)' = 12x -4\)
If the constant c between 1 and 9 such that the average value of the function f(x) on the interval (1,9], then,
\(f(c)'=12c-4\)
Using Lagrange's mean value theorem,
\(f(c)'=\dfrac{f(9)-f(1)}{9-1}\\12c-4=\dfrac{452-4}{9-1}\\12c=54+4\\c=\dfrac{60}{12}\\c=5\)
Thus, the value of constant c between 1 and 9 such that the average value of the function f(x) on the interval [1,9] is equal to is 5.
Learn more about the mean value theorem here;
https://brainly.com/question/15115079
#SPJ1
Answer:
5.5402
Step-by-step explanation:
First you need to find the average value of the function, you can use a calculator to do that, which you will find is 164.
The questions asks you to find a number between 1 and 9 so that f(c) (which is just f(x)) equals the average value of the function.
Since you already know the average value (164), you can set the equation equal to 164 and solve for x, which should give you 5.5402.
If you want more information: the function equals the average value, which is 164=6x^2-4x+2, is the equation you want to set up and solve for x.
You may get two answers and I can't explain why because I don't understand it that well, just use the one that is in the 1 to 9 range.
The second answer should be negative which is out of the 1 to 9 range, which leaves you with the other number that rounds up to 5.5402
I hope this helps any other struggling students
The following data summarizes results from 945 pedestrian deaths that were caused by accidents. If one of the pedestrian deaths is randomly selected, find the probability that the pedestrian was intoxicated or the driver was intoxicated.
Pedestrian
intoxicated not intoxicated
Driver intoxicated 64 68
not intoxicated 292 521
Answers
Answer:
37.67% probability that the pedestrian was intoxicated or the driver was intoxicated.
Step-by-step explanation:
A probability is the number of desired outcomes divided by the number of total outcomes.
In this question:
945 accidents.
In 64 of them, the pedestian was intoxicated.
In 292 of them, the driver was intoxicated.
Probability that the pedestrian was intoxicated or the driver was intoxicated.
(64+292)/945 = 0.3767
37.67% probability that the pedestrian was intoxicated or the driver was intoxicated.