convert 77/80 to a decimal
Answers
Answer:
Attached file
Step-by-step explanation:

Related Questions
Dean Webber purchased 4 smoothies for $19.60. At this price, what is the cost per smoothie?
Answers
4.9 is the cost per smoothie
Answer:
$ 4.90 per smoothie
Step-by-step explanation:
The total cost of all of the 4 smoothies is $19.60. So, to find the answer you need to divide 19.60 with 4 and you'll get 4.9 or as dollars $4.90.
Pls help meh pls, im not good at math, but if you help me I can help with English or something like that
NO LINKS OR YOU WILL GET REPORTED
Find the area of the figure. (Sides meet at right angles.)

Answers
Answer:
52 i think
Step-by-step explanation:
big rectangle is 40
little rectangle is 12
what the dog doing ?
Answers
The dog is playing with his chew toy!
Answer:
Explanation
Step-by-step explanation:
In general, dogs can run 15-20 mph
humans can run 6-8 mph
You are significantly slower than the dog,
the fastest human is around 27 miles per hour, unfortunately, even if you were this fast
the fastest dog can run 40 miles per hour as an estimate
even house cats can run at 30 mph maximum if they really wanted,
You have no chance of outrunning this dog, and barely a chance of outsmarting it if that option was available, in conclusion, the dog is chasing you at a speed of around 30 mph about 6-7x more than your own speed with no chance of outrunning it(the dog).
How many blocks with dimensions of 3x1x1 can fit in a unit cube?
x
1
2
3
Ο Ο Ο Ο
6
9
Answers
Answer:
None
Step-by-step explanation:
None. A unit cube has dimensions 1 by 1 by 1, so it could not contain a rectangle of dimensions 3 by 1 by 1.
I’m supposed to put theses least to greatest according to their volumes assume the variable h has the same value for each figure
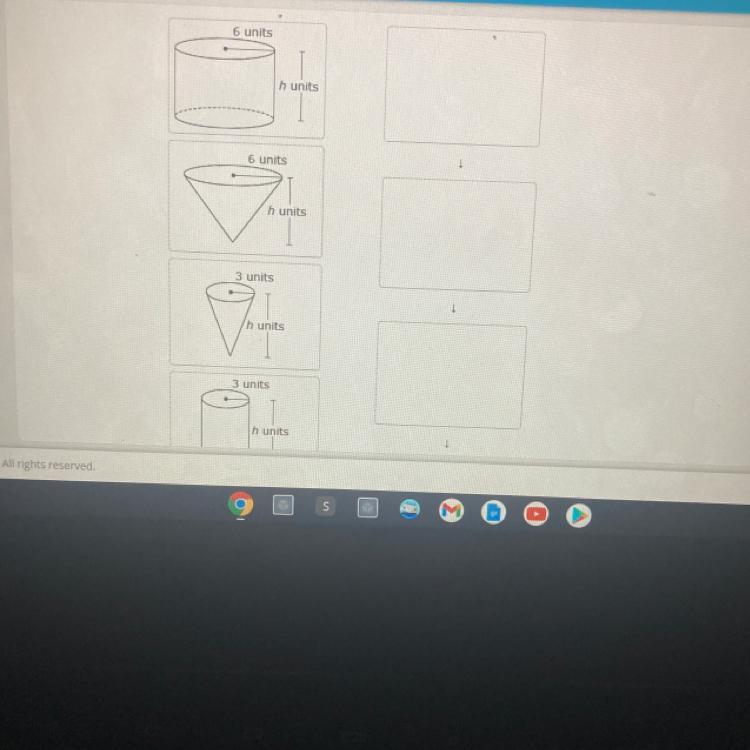
Answers
Hello there. To solve this question, we'll have to remember some properties about finding volumes of polyhedrons.
Given the following figures, we have to order them from least to greatest with respect to volume:
In this case, as h is the same for all the polyhedrons, we simply have to compare their volumes with respect to the constant multiplying h.
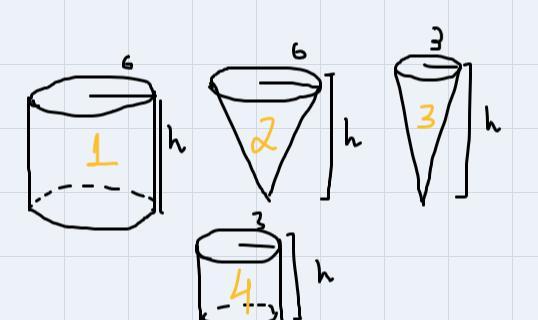
For a cylinder of radius r and height h, its volume is given by:
\(V_{\text{cylinder}}=\pi\cdot r^2\cdot h\)For a cone with radius r and height h, its volume is given by:
\(V_{\text{cone}}=\frac{\pi\cdot r^2\cdot h}{3}\)Labelling each of the figures (go back to the image), we calculate their volume as follows:
Since h is the same, we compare the constants. We know that pi is approximately equal to 3.14, therefore:
The order we have to put these figures is 3, 4, 2, 1.
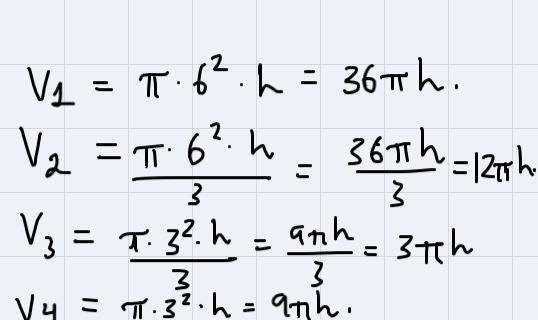

Identify the null and alternative hypothesis in the following scenario.
To determine if battery 1 lasts longer than battery 2, the mean lasting times, of the two competing batteries are compared. Twenty batteries of each type are randomly sampled and tested. Both populations have normal distributions with unknown standard deviations.
a. H0:μ1≥μ2; Ha:μ1<μ2
b. H0:μ1≤−μ2; Ha:μ1>−μ2
c. H0:μ1≥−μ2; Ha:μ1<−μ2
d. H0:μ1=μ2; Ha:μ1≠μ2
e. H0:μ1≤μ2; Ha:μ1>μ2
Answers
Answer:
H0 : u1 = u2 ; H1 : u1 ≠ u2 , or specifically u1 > u2
Step-by-step explanation:
Null Hypothesis is the neutral hypothesis , stating no difference from assumed value, (or in this case no difference between both batteries' mean life)
Alternate Hypothesis is the special case hypothesis, stating difference from assumed value , (or in this case states difference between both batteries' mean life)
Let mean life of battery 1 & battery be b = u1 & u2 , respectively.
Null Hypothesis [ H0 ] : u1 = u2
Alternate Hypothesis [ H1 ] : u1 ≠ u2 , or specifically u1 > u2 { To determine if battery 1 lasts longer than battery 2 }
1. Find the area of the composite figure below. Make sure you show your work neatly for full
credit.
(3.5)
18 in.
18 in.
9 in.
36 in.
18 in.
Answers
The calculated area of the composite figure is 85 cm².
How to calculate the the area of the composite figureFrom the question, we have the following parameters that can be used in our computation:
The composite figure (see attachment)
Where, we have
Rectangle:
Area = length × width.
Therefore, the area of the rectangle is 10 cm × 6 cm = 60 cm².
Triangle:
Area = (1/2) × base × height.
Therefore, the area of the triangle is (1/2) × 5 cm × 10 cm = 25 cm².
To find the total area of the composite figure, we add the areas of the rectangle and the triangle:
Total Area = Area of Rectangle + Area of Triangle
= 60 cm² + 25 cm²
= 85 cm².
Therefore, the area of the composite figure is 85 cm².
Learn more about area at
brainly.com/question/25292087
#SPJ1

Find the perimeter of this shape

Answers
The perimeter of the given shape as represented in the task content is; 29 cm.
What is the perimeter of the given shape?It follows from the task content that the perimeter of the given shape on the centimeter grid as required is to be determined.
Since each grid line has 1cm as it's length;
The perimeter of the shape is the sum of all side lengths of the shape;
Perimeter, P = 6+2+3+2+2+1+3+2+2+2+2+1
P = 29 cm
Hence, the perimeter of the shape is; 29 cm.
Read more on perimeter of a shape;
https://brainly.com/question/303508
#SPJ1
James wants to have earned $6,180 amount of interest in 28 years. Currently he finds
that his annual interest rate is 6.12%. Calculate how much money James needs to invest
as his principal in order to achieve this goal.
Answers
Answer:
$3606.44
Step-by-step explanation:
The question asks us to calculate the principal amount that needs to be invested in order to earn an interest of $6180 in 28 years at an annual interest rate of 6.12%.
To do this, we need to use the formula for simple interest:
\(\boxed{I = \frac{P \times R \times T}{100}}\),
where:
I = interest earned
P = principal invested
R = annual interest rate
T = time
By substituting the known values into the formula above and then solving for P, we can calculate the amount that James needs to invest:
\(6180 = \frac{P \times 6.12 \times 28}{100}\)
⇒ \(6180 \times 100 = P \times 171.36\) [Multiplying both sides by 100]
⇒ \(P = \frac{6180 \times 100}{171.36}\) [Dividing both sides of the equation by 171.36]
⇒ \(P = \bf 3606.44\)
Therefore, James needs to invest $3606.44.
Write the following linear equation in function notation y=7x-2
Answers
Answer:
The function notation is when we represent one of the coordinate points as a function of the other ones.
In the general case, we will have:
y = f(x)
Now, we have that:
y = 7*x - 2
Then the function notation will be:
y = f(x) = 7*x - 2
or simply
f(x) = 7*x - 2
Answer:
f(x)= 7x-2
Step-by-step explanation:
I did the quiz and got it right.
7 (w+8) = 2w+10
What is the value of w makes the equation true? Enter the answer in the box.
Test.mapnwea.org.
Answers
Answer:
w = -46/5
Step-by-step explanation:
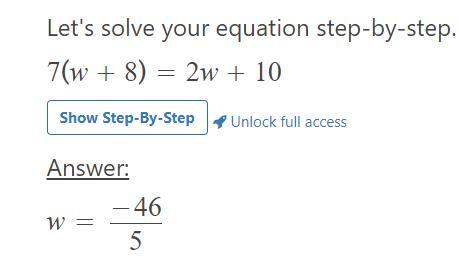
Answer:
w=-9.2
Step-by-step explanation:
7(w+8)=2w+10
7w+56=2w+10
7w-2w=10-56
5w=-46
w=-9.2
What is the equation of the line that passes through the point (3, 5) and has a slope of 1?
Answers
Step-by-step explanation:
in what form do we need the equation ?
slope-intercept ?
that would be
y = ax + b
with "a" being the slope and "b" being the y-intercept (the y-value when x = 0).
in any case, since we have the slope and a point, we can start with the point-slope form :
y - yp = a(x - xp)
"a" is again the slope, and (xp, yp) is the given point.
so,
y - 5 = 1×(x - 3) = x - 3
adding 5 to both sides gives us
y = x + 2
and that is our desired equation in slope-intercept form.
awnser the qusetion 9iu523hb5hn33

Answers
The order of the matrices of each product is given as follows:
AB is nonexistent, BA is nonexistent.
How to apply multiplication of matrices?Multiplication of matrices is applied multiplying the rows of the first matrix by the columns of the second matrix, and hence the number of columns of the first matrix must be equal to the number of rows of the second matrix.
For the product AB, we have that:
A has four columns.B has two rows.Hence the product is nonexistent.
For the product BA, we have that:
B has four columns.A has two rows.Hence the product is nonexistent.
More can be learned about multiplication of matrices at https://brainly.com/question/24274686
#SPJ1
PLEASE HELP!!! Solve 5sin(π/3x)=3 for the four smallest positive solutions
Answers
This one's a special case of a right angled triangle with sides (3, 4, and 5 units)
Back to the problem :\(\qquad\displaystyle \tt \dashrightarrow \: 5 \sin \bigg( \frac{ \pi}{3} x \bigg) = 3\)
\(\qquad\displaystyle \tt \dashrightarrow \: \sin \bigg( \frac{ \pi}{3} x \bigg) = \frac{3}{5} \)
Now, check the triangle, sin 37° = 3/5
therefore,
\(\qquad\displaystyle \tt \dashrightarrow \: \sin \bigg( \frac{ \pi}{3} x \bigg) = \sin(37 \degree) \)
[ convert degrees on right side to radians ]
\(\qquad\displaystyle \tt \dashrightarrow \: \sin \bigg( \frac{ \pi}{3} x \bigg) = \sin \bigg(37 \degree \times \frac{ \pi}{180 \degree} \bigg ) \)
There are three more possible values as :
\(\qquad\displaystyle \tt \dashrightarrow \: \sin( \theta) = \sin(\pi - \theta) \)
\(\qquad\displaystyle \tt \dashrightarrow \: sin( \theta) = \sin \bigg( { 2\pi}{} + \theta \bigg) \)
\(\qquad\displaystyle \tt \dashrightarrow \: sin( \theta) = \sin \bigg( \frac{ 3\pi}{} - \theta\bigg) \)
Equating both, we get : First value :\(\qquad\displaystyle \tt \dashrightarrow \: \frac{ \pi}{3} x = 37 \times \frac{ \pi}{180} \)
\(\qquad\displaystyle \tt \dashrightarrow \: x = 37 \times \frac{ \cancel \pi}{180} \times \frac{3}{ \cancel \pi} \)
\(\qquad\displaystyle \tt \dashrightarrow \: x = \frac{37}{60} \)
or in decimals :
\(\qquad\displaystyle \tt \dashrightarrow \: x = 0.616666... = 0.6167\)
[ 6 repeats at third place after decimal, till four decimal places it would be 0.6167 after rounding off ]
similarly,
Second value :\(\qquad\displaystyle \tt \dashrightarrow \: \pi - \frac{ \pi}{3} x = 37 \times \frac{ \pi}{180} \)
\(\qquad\displaystyle \tt \dashrightarrow \: \pi \bigg(1 - \frac{x}{3} \bigg ) = 37 \times \frac{ \pi}{180} \)
\(\qquad\displaystyle \tt \dashrightarrow \: 1 - \frac{x}{3} = \frac{37}{180} \)
\(\qquad\displaystyle \tt \dashrightarrow \: - \frac{x}{3} = 0.205 - 1\)
\(\qquad\displaystyle \tt \dashrightarrow \: \frac{x}{3} = 0.795\)
\(\qquad\displaystyle \tt \dashrightarrow \: x = 3 \times 0.795\)
\(\qquad\displaystyle \tt \dashrightarrow \: x = 2.385\)
Third value :\(\qquad\displaystyle \tt \dashrightarrow \: 2\pi + \frac{ \pi}{3} x = 37 \times \frac{ \pi}{180} \)
\(\qquad\displaystyle \tt \dashrightarrow \: \pi \bigg(2 + \frac{x}{3} \bigg ) = 37 \times \frac{ \pi}{180} \)
\(\qquad\displaystyle \tt \dashrightarrow \: 2 + \frac{x}{3} = \frac{37}{180} \)
\(\qquad\displaystyle \tt \dashrightarrow \: \frac{x}{3} = 0.205 - 2\)
\(\qquad\displaystyle \tt \dashrightarrow \: \frac{x}{3} = - 1.795\)
\(\qquad\displaystyle \tt \dashrightarrow \: x = 3 \times -1 .795\)
\(\qquad\displaystyle \tt \dashrightarrow \: x = -5.385\)
Fourth value :\(\qquad\displaystyle \tt \dashrightarrow \: 3 \pi - \frac{ \pi}{3} x = 37 \times \frac{ \pi}{180} \)
\(\qquad\displaystyle \tt \dashrightarrow \: \pi \bigg(3 - \frac{x}{3} \bigg ) = 37 \times \frac{ \pi}{180} \)
\(\qquad\displaystyle \tt \dashrightarrow \: 3 - \frac{x}{3} = \frac{37}{180} \)
\(\qquad\displaystyle \tt \dashrightarrow \: - \frac{x}{3} = 0.205 - 3\)
\(\qquad\displaystyle \tt \dashrightarrow \: \frac{x}{3} = 2.795\)
\(\qquad\displaystyle \tt \dashrightarrow \: x = 3 \times 2.795\)
\(\qquad\displaystyle \tt \dashrightarrow \: x = 8.385\)
" x can have infinite number of values here with the same result, here are the four values as you requested "
I hope it was helpful ~

how do I solve this triangle problem!!!

Answers
Answer:
Angles 1 and 2 are both 60, and angle 3 is 120
Step-by-step explanation:
Answer:
The total if a triangle is 180, for a right angle so 180 subtract the number u have and 90 plus the number u have and the number u got
Write the fraction as a mixed number 10/20
Answers
Which inequality represents the situation described below?
The distance, d, is less than 200 miles.
A. d ≥ 200
B. d > 200
C. d ≤ 200
D. d < 200
Answers
Hello!
The distance, d, is less than 200 miles.
B. d > 200
Find the square root of: 2 + sqrt5
Answers
Answer:
3.65
Step-by-step explanation:
The square root of 2 is 1.4 and the square root of 5 is 2.2 adding that together you get 3.6
PLEASE HELP
The table of values represents an exponential function.
What is the y-coordinate of -3f(x-1) when x = 0
Enter your answer in the box.
SEE PHOTO

Answers
The y-coordinate of -3f(x-1) when x = 0 is -63
What is the y-coordinate of -3f(x-1) when x = 0From the question, we have the following parameters that can be used in our computation:
The table of values
So, we have
-3f(x - 1)
When x = 0, we have
y = -3f(0 - 1)
This gives
y = -3f(-1)
From the table, we have
y = -3 * 21
Evaluate
y = -63
Hence, the y-coordinate is -63
Read more about exponential function at
https://brainly.com/question/2456547
#SPJ1
To a set of five grades with an average of 7.31, the following grades are added 4.47 and 9.15 What is the new average?
Answers
Answer:
New mean average of 7 grades = 7.17 (Approx.)
Step-by-step explanation:
Given:
Mean average of 5 grades = 7.31
Number of grades = 5
New grades = 4.47 and 9.15
Find:
New mean average of 7 grades
Computation:
Total of old grades = Mean average of 5 grades x Number of grades
Total of old grades = 7.31 x 5
Total of old grades = 36.55
Total of new grades = Total of old grades + 4.47 + 9.15
Total of new grades = 36.55 + 4.47 + 9.15
Total of new grades = 50.17
New mean average of 7 grades = 50.17 / 7
New mean average of 7 grades = 7.167
New mean average of 7 grades = 7.17 (Approx.)
) Find the gradient of a line joining the points 1) (1,-1) and (4,9) 2) (5,1)and(2-2) 2) Find the x and y intercepts for the equation 3y = 2x-2
Answers
The gradient of the line joining the points (1,-1) and (4,9) is 10/3, while the gradient of the line joining (5,1) and (2,-2) is 1. The x-intercept of the equation 3y = 2x - 2 is 1, and the y-intercept is -2/3. These calculations follow the formula for gradient and the methods for finding intercepts in linear equations.
1) To find the gradient of a line joining two points, you can use the formula: gradient = (change in y)/(change in x).
Given the points (1,-1) and (4,9), the change in y is 9 - (-1) = 10 and the change in x is 4 - 1 = 3.
Therefore, the gradient of the line joining these points is 10/3.
2) Similarly, to find the gradient of a line joining two points (5,1) and (2,-2), we can use the same formula. The change in y is -2 - 1 = -3 and the change in x is 2 - 5 = -3.
Therefore, the gradient of the line joining these points is -3/-3 = 1.
3) To find the x-intercept, we set y to 0 and solve for x.
Given the equation 3y = 2x - 2, if we substitute y with 0, we have 3(0) = 2x - 2, which simplifies to 0 = 2x - 2.
To solve for x, we can add 2 to both sides: 0 + 2 = 2x - 2 + 2, which gives us 2 = 2x.
Dividing both sides by 2, we get x = 1.
Therefore, the x-intercept of the equation 3y = 2x - 2 is 1.
To find the y-intercept, we set x to 0 and solve for y.
Using the same equation, if we substitute x with 0, we have 3y = 2(0) - 2, which simplifies to 3y = -2.
To solve for y, we can divide both sides by 3: (3y)/3 = (-2)/3, which gives us y = -2/3.
Therefore, the y-intercept of the equation 3y = 2x - 2 is -2/3.
For more such questions gradient,Click on
https://brainly.com/question/23016580
#SPJ8
increase R700 in the Ratio 3:2
Answers
Step-by-step explanation:
³93521586335445555554555554488807799654
2.) Write a verbal expression that
represents the algebraic expression.
m/12
Answers
Answer:
A number divided by twelve
Step-by-step explanation:
Compare the Poisson approximation with the correct binomial probability for the following cases:
(a) P{X=2} when n = 8, p =0.1;
(b) P{X=9} when n = 10, p = 0.95;
(c) P{X=0} when n = 10,p=0.1;
(d) P{X=4} when n = 9, p =0.2;
Answers
(a) The Poisson approximation is 0.019 and the binomial probability is 0.134. (b) The Poisson approximation is 0.187 and the binomial probability is 0.039. (c) The Poisson approximation is 0.135 and the binomial probability is 0.348. (d) The Poisson approximation is 0.167 and the binomial probability is 0.206.
(a) The Poisson approximation is
P(X=2) =\((e^(-0.8)*(0.8^2))/2!\)
= 0.019.
The binomial probability is
P(X=2) = \((8C2)*(0.1^2)*(0.9^6)\)
= 0.134.
(b) The Poisson approximation is
P(X=9) = \((e^(-9.5)*(9.5^9))/9!\)
= 0.187.
The binomial probability is
P(X=9) = \((10C9)*(0.95^9)*(0.05^1)\)
= 0.039.
(c) The Poisson approximation is
P(X=0) = \((e^(-1)*(1^0))/0! = 0.135.\)
The binomial probability is
P(X=0) = \((10C0)*(0.1^0)*(0.9^10)\)
= 0.348.
(d) The Poisson approximation is
P(X=4) = \((e^(-1.8)*(1.8^4))/4!\)
= 0.167.
The binomial probability is
P(X=4) = \((9C4)*(0.2^4)*(0.8^5)\)
= 0.206.
The Poisson approximation is used when the number of trials is large and the probability of success is small. It is a good approximation for the binomial distribution in these cases. When n is smaller and p is larger, the Poisson approximation is not as accurate. In the cases provided, the Poisson approximation is close to the binomial probability when n is small and p is small, but it is not as accurate when n is larger and p is closer to 1. The Poisson approximation is always smaller than the binomial probability.
Learn more about probability here
https://brainly.com/question/30034780
#SPJ4
Jack leaves home for school on his bike every day at 6 a.m., travelling at 32 km/h.
One day he forgot his homework, which his mother discovered in the car 15 minutes after he had left.
She immediately left home and chased after Jack, travelling at 52 km/h.
At what time did she catch up to him?
Answers
Let's break down the information given:
- Jack's speed: 32 km/h
- Jack left at 6 a.m.
- Jack's mother's speed: 52 km/h
- Jack's mother discovered the homework 15 minutes after Jack had left.
First, we need to convert the 15 minutes of delay into hours. There are 60 minutes in an hour, so 15 minutes is equal to 15/60 = 0.25 hours.
Now, let's calculate the time it took for Jack's mother to catch up to him:
Distance traveled by Jack in 0.25 hours = Jack's speed * time
Distance traveled by Jack in 0.25 hours = 32 km/h * 0.25 hours = 8 km
Since Jack's mother is traveling at a faster speed than Jack, she will cover this distance faster. To determine the time it takes for her to catch up, we divide the distance by her speed:
Time taken for Jack's mother to cover 8 km = Distance / Speed
Time taken for Jack's mother to cover 8 km = 8 km / 52 km/h ≈ 0.154 hours
Now, we can add this time to the initial delay of 0.25 hours to find out when Jack's mother catches up to him:
Time when Jack's mother catches up to him = 6 a.m. + 0.25 hours + 0.154 hours
To simplify the calculation, we can convert the minutes into hours:
0.25 hours + 0.154 hours = 0.404 hours
Converting back to minutes:
0.404 hours * 60 minutes/hour ≈ 24.24 minutes
Adding this to the initial time of 6 a.m.:
Time when Jack's mother catches up to him ≈ 6:24 a.m.
Therefore, Jack's mother catches up to him at approximately 6:24 a.m.
Rearange the equation so n is the independent variable m+1=-2n+6 ? M= what
Answers
Answer:
m = - 2n + 5
Step-by-step explanation:
Given the equation:
m+1=-2n+6
Rearrange the equation so that n is the independent variable
The independent variable is the predictor variable, Hence causes a change in the value of predicted variable obtained.
m+1=-2n+6
m = - 2n + 6 - 1
m = - 2n + 5
m = - 2n + 5
The general form of a regression equation:
y = ax + b
Where y = dependent variable
x = independent variable ; a = Coefficient of slope ; b = intercept
Hence, the equation : m = - 2n + 5
The sum of two numbers is 12. The difference of the two numbers is 6. What are the two numbers?
Answers
Answer:
3 and 9
Step-by-step explanation:
x+y=12
y-x=6
y-x=6
+x. +x
y=6+x
x+(6+x)=12
6+2x=12
-6. -6
2x=6
/2. /2
x=3
3+y=12
-3. -3
y=9
Hopes this helps please mark brainliest
Marcus was showing how he solved a division problem with the area model below. His pen exploded ink on some of his work.
What is the divisor that is covered with ink on the left side of the model?
A. 100
B. 80
C. 56
D. 29

Answers
Answer:
C
Step-by-step explanation:
60 is what percent of 75
Answers
answer: The answer is 80%
Ziv's taxicab ride cost $33. He left a 15% tip.
What was the total cost of the taxicab ride with tip?
Enter your answer in the box.
Answers
Answer:
37.95
Step-by-step explanation:
33 x 15%
0.15 x 33 = 4.95
33 + 4.95 = 37.95