Construct a 95% confidence interval for the true average monthly salary earned by all employees of People Plus Pty, if it was found that the average monthly salary earned by a sample of 19 employees of the company was R18 500, with a standard deviation of R1 750. Interpret your answer
Answers
We can be 95% confident that the true average monthly salary earned by all employees of People Plus Pty is between R16 234.49 and R20 765.51. This means if created for several samples of the same size taken from the population, would contain the actual population mean.
To construct a 95% confidence interval for the true average monthly salary earned by all employees of People Plus Pty, we can use the following formula:
CI = x ± t(α/2, n-1) * (s/√n)
where:
x = sample mean = R18 500
s = sample standard deviation = R1 750
n = sample size = 19
t(α/2, n-1) = t-score at α/2 and n-1 degrees of freedom
Using a t-table or calculator with 18 degrees of freedom (n-1), we can find the t-score at α/2 = 0.025 to be 2.101.
Plugging in the values, we get:
CI = 18500 ± 2.101 * (1750/√19)
= (16234.49, 20765.51)
Therefore, we can be 95% confident that the true average monthly salary earned by all employees of People Plus Pty is between R16 234.49 and R20 765.51.
This means that if we were to take multiple samples of the same size from the population and construct 95% confidence intervals for each sample mean, about 95% of those intervals would contain the true population mean.
Learn more about confidence interval at https://brainly.com/question/18915814
#SPJ11
Related Questions
through: (-1,0), parallel to y = 4x
Answers
Answer:
Find the slope of the original line and use the point-slope formula y−y1=m(x−x1)to find the line parallel to y=4x.
y=4x+4
Step-by-step explanation:

Two types of alien live on the planet Starlight: Zoomas have 3 eyes and 2 legs and Popsies have 4 eyes and 5 legs. How many of each type of alien might there be if there are 38 eyes and 37 legs
Answers
Answer:
Below
Step-by-step explanation:
(3y + 2l )z + (4y + 5l) p = 38y+37 l <=======given ( y = eyes , l = legs)
z 2l + p5l = 37 l <===separating out the' l ' part
2z + 5p = 37
3y z + 4y p = 38y <====== taking out the 'y' part
3z + 4 p = 38 Solve the two underlined simultaneous equations
multiply first one by - 1.5 then add to second one to get:
-3z -7.5p = - 55.5 <===== solve for p
-3.5 p = - 17.5
p = 5 then z = 6
The mean cost of a five pound bag of shrimp is 42 dollars with a variance of 49. If a sample of 54 bags of shrimp is randomly selected, what is the probability that the sample mean would be less than 43.4 dollars? Round your answer to four decimal places.
Answers
The probability that the sample mean would be less than 43.4 dollars is 0.9292.
What is a probability?Probability is the occurence of likely events. It is the area of mathematics that deals with numerical estimates of the likelihood that an event will occur or that a statement is true.
From the information, the mean cost of a five pound bag of shrimp is 42 dollars with a variance of 49 and a sample of 54 bags of shrimp is randomly selected.
Therefore, the probability will be:
P(x < 43.4)
Using normal distribution
= P(z < 43.4 - Mean( / 7/✓54)
= P(z < 43.4 - 42( / 7/✓54)
= P(z < 1.4697)
= 0.9292
The probability is 0.9292.
Learn more about probability on:
brainly.com/question/24756209
#SPJ1
Drawing from an ordinary 52-card deck of cards, you will draw four cards at once. What is the probability of drawing 2 pairs?
Answers
The probability of drawing 2 pairs is 0.457
To calculate the probability of drawing 2 pairs from a standard 52-card deck, we can use the following steps:
Choose 2 ranks out of 13 for the two pairs.
Choose 2 suits out of 4 for the first pair.
Choose 2 suits out of the remaining 4 for the second pair.
Choose any 2 cards from the remaining 44 cards.
Using the formula for combinations, we can calculate the number of ways to choose these cards:
C(13,2) * C(4,2) * C(4,2) * C(44,2) = 123,552
The total number of ways to draw any 4 cards from a deck of 52 is:
C(52,4) = 270,725
Therefore, the probability of drawing 2 pairs is:
123,552 / 270,725 ≈ 0.457 or about 45.7%.
Lean more about Probability here
https://brainly.com/question/32117953
#SPJ4
Express the answers to the following operations with the proper number of significant figures. (a) 8.370×1.3 ×10 (b) 4.265/2.0 (c) (1.2588×10 ^3)×(1.06×10 ^−2) (d) (1.11) ^1/2
Answers
The answers, rounded to the appropriate number of significant figures, are as follows:
(a) 1.088 ×\(10^2\)
(b) 2.132
(c) 1.3331 ×\(10^1\) and
(d) 1.05.
Let's calculate the answers to the given operations using the appropriate number of significant figures.
(a) 8.370×1.3×10
To perform this multiplication, we multiply the decimal numbers and add the exponents of 10:
8.370 × 1.3 × 10 = 10.881 × 10 = 1.0881 × \(10^2\)
Since the original numbers have four significant figures, we round the final answer to four significant figures:
1.088 × \(10^2\)
(b) 4.265/2.0
For division, we divide the decimal numbers:
4.265 ÷ 2.0 = 2.1325
Since both numbers have four significant figures, the answer should be rounded to four significant figures:
2.132
(c) (1.2588×\(10^3\))×(1.06×\(10^-^2\))
To multiply these numbers, we multiply the decimal numbers and add the exponents:
(1.2588 × \(10^3\)) × (1.06 × \(10^-^2\)) = 1.333128 × \(10^1\)
Since the original numbers have five significant figures, we round the final answer to five significant figures:
1.3331 × \(10^1\)
(d) \((1.11)^(^1^/^2^)\)
To calculate the square root, we raise the number to the power of 1/2:
\((1.11)^(^1^/^2^)\)= 1.0524
Since the original number has three significant figures, the answer should be rounded to three significant figures:
1.05
It's important to note that the significant figures in a result are determined by the original data and the operations performed. The final answers provided above reflect the appropriate number of significant figures based on the given information and the rules for significant figures.
For more such information on: significant figures
https://brainly.com/question/30169
#SPJ8
You picked two marbles from a bag and record their color. How can you make your selections independent events? Dependent events?
Answers
Answer:
Let's suppose the next case:
We have a bag, where there are 5 red marbles, and 5 blue marbles.
We have a total of 10 marbles.
Suppose that we pick a marble and we do not replace it, and suppose that the first one is a red marble.
Then now we have in the bag a total of 4 red marbles and 5 blue marbles.
Now let's find the probability of picking a blue marble, this will be equal to the quotient between the number of blue marbles (5) and the total number of marbles (9)
P = 5/9
Now, suppose that instead of a red marble in the first pick, we had a blue marble.
Then now we have 4 blue marbles and 5 red marbles in the bag.
Again, the probability of picking a blue marble will be equal to the quotient between the number of blue marbles (4) and total numbergof marbles (9)
P = 4/9
Then the first pick does affect the probabilities for the second pick, this means that if we do not replace the first marble we pick, then the events will be dependent.
Now, if we replaced the first marble we picked (we put it again in the bag) then the number of blue marbles and red marbles is always the same, then in this case bot events will be independent (the first event will not affect the second event)
4y^5-6y+8y^2-1 for y = -1
Answers
Answer:9
Step-by-step explanation:
A triangle in which one angle is greater than 90 degree is called______.
Answers
An obtuse angle is some angle x such that 90 < x < 180.
An obtuse triangle has one obtuse angle. The other two angles are acute (they are less than 90 degrees).
An obtuse triangle is a type of triangle that has one angle greater than 90 degrees.
An obtuse triangle is a type of triangle that has one angle greater than 90 degrees. In other words, one of the angles in an obtuse triangle is 'blunt' or 'dull' and measures more than 90 degrees. The other two angles in an obtuse triangle are acute angles, which means they are less than 90 degrees.
The sum of the measures of the three angles in any triangle is always 180 degrees. In an obtuse triangle, the sum of the measures of the three angles is greater than 180 degrees because one of the angles is greater than 90 degrees.
For example, if we have an obtuse triangle with angles measuring 100 degrees, 40 degrees, and 40 degrees, the sum of the angles would be 180 degrees, with one angle greater than 90 degrees.
Learn more:About obtuse triangle here:
https://brainly.com/question/2617159
#SPJ11
what is the maximum difference in radius for 295/75r22 5 trailer tires
Answers
The maximum difference in radius for 295/75R22.5 trailer tires is 0.625 inches.
The tire size 295/75R22.5 represents certain measurements. The first number, 295, refers to the tire's width in millimeters. The second number, 75, represents the aspect ratio, which is the tire's sidewall height as a percentage of the width. The "R" stands for radial construction, and the number 22.5 denotes the diameter of the wheel in inches.
To calculate the maximum difference in radius, we need to determine the difference between the maximum and minimum radius values within the given tire size. The aspect ratio of 75 indicates that the sidewall height is 75% of the tire's width.
To find the maximum radius, we can calculate:
Maximum Radius = (Width in millimeters * Aspect Ratio / 100) + (Wheel Diameter in inches * 25.4 / 2)
For the given tire size, the maximum radius is:
Maximum Radius = (295 * 75 / 100) + (22.5 * 25.4 / 2) ≈ 388.98 mm
Similarly, we can find the minimum radius by considering the minimum aspect ratio value (in this case, 75) and calculate:
Minimum Radius = (295 * 75 / 100) + (22.5 * 25.4 / 2) ≈ 368.98 mm
The difference in radius between the maximum and minimum values is:
Difference in Radius = Maximum Radius - Minimum Radius ≈ 388.98 mm - 368.98 mm ≈ 20 mm
Converting this to inches, we have:
Difference in Radius ≈ 20 mm * 0.03937 ≈ 0.7874 inches
Therefore, the maximum difference in radius for 295/75R22.5 trailer tires is approximately 0.7874 inches, which can be rounded to 0.625 inches.
To learn more about radius
https://brainly.com/question/27696929
#SPJ11
Use the function y=3/2x +3 to
complete the table of values.
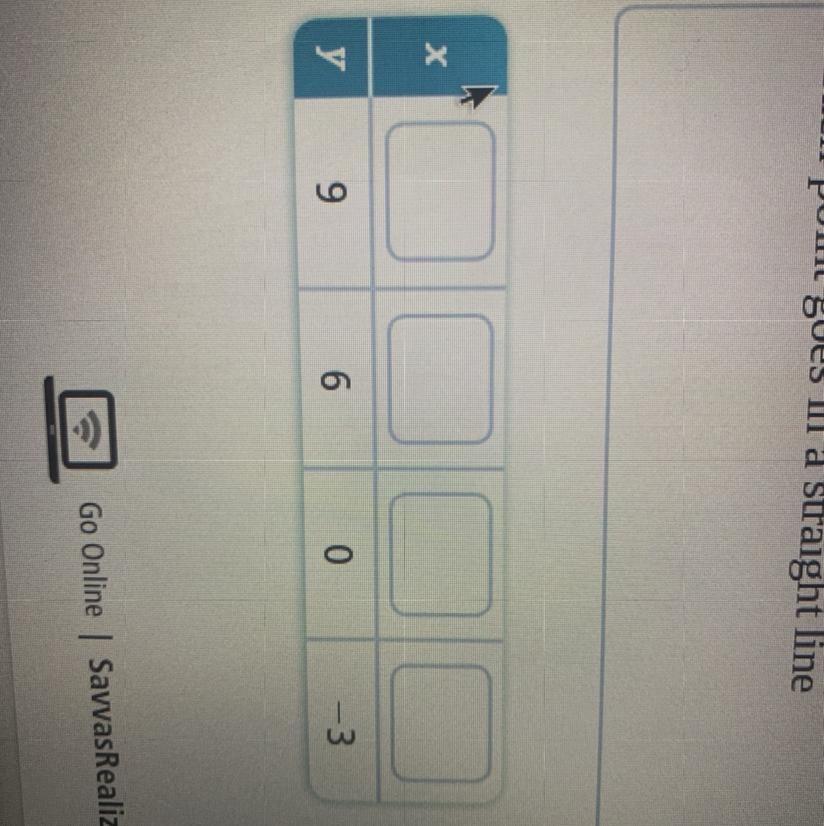
Answers
Answer:
Please check the explanation.
Step-by-step explanation:
Given the function
\(y=\frac{3}{2}x\:+3\)
Putting all the values of y=9, 6, 0, and -3 to complete the tableFOR y=9
\(y=\frac{3}{2}x\:+3\)
putting y=9
\(9=\frac{3}{2}x+3\)
switch sides
\(\frac{3}{2}x+3=9\)
subtract 3 from both sides
\(\frac{3}{2}x+3-3=9-3\)
\(\frac{3}{2}x=6\)
\(3x=12\)
\(x=4\)
Hence,
when y=9, x=4
FOR y=6
\(y=\frac{3}{2}x\:+3\)
putting y=6
\(6=\frac{3}{2}x+3\)
switch sides
\(\frac{3}{2}x+3=6\)
subtract 3 from both sides
\(\frac{3}{2}x+3-3=6-3\)
\(\frac{3}{2}x=3\)
\(3x=6\)
\(x=2\)
Hence,
when y=6, x=2
FOR y=0
\(y=\frac{3}{2}x\:+3\)
putting y=0
\(0=\frac{3}{2}x+3\)
switch sides
\(\frac{3}{2}x+3=0\)
subtract 3 from both sides
\(\frac{3}{2}x+3-3=0-3\)
\(\frac{3}{2}x=-3\)
\(3x=-6\)
\(x=-2\)
Hence,
when y=0, x=-2
FOR y=-3
\(y=\frac{3}{2}x\:+3\)
putting y=-3
\(-3=\frac{3}{2}x+3\)
switch sides
\(\frac{3}{2}x+3=-3\)
subtract 3 from both sides
\(\frac{3}{2}x+3-3=-3-3\)
\(\frac{3}{2}x=-6\)
\(3x=-12\)
\(x=-4\)
Hence,
when y=-3, x=-4
Hence, the table becomes:
x y
9 4
6 2
0 -2
-3 -4
Can someone help me with this , thank you :)

Answers
What is an equation of the line that passes through the points (5 , -6) and (-5 , -2)?
I will give brainliest! thank you
Answers
Answer:
Step-by-step explanation: Plug coordinates into y=ax+b
Simultaneous equations
-6=5a+b
-2=-5a+b
So y=-0.4x-4
BRAINLIEST PLEASE THX
how many 9 are there between 1 and 100?
Answers
Answer:
20
Step-by-step explanation:
To determine the number of 9s between 1 and 100, we can consider the numbers from 1 to 99 since we want to exclude 100.
In the range from 1 to 99, we can observe the following patterns:
There is one 9 in each of the units' places (9, 19, 29, ..., 89, 99), giving us 10 occurrences.
There is one 9 in each of the tens' places (90, 91, 92, ..., 99), giving us 10 occurrences.
Therefore, there are a total of 10 + 10 = 20 occurrences of the digit 9 between 1 and 100.
What is the value of x to the nearest tenth?
29.6
X
73°
33°
Answers
True or False: All horizontal lines have a y-intercept.
Answers
Answer:
If you are looking at a graph then yes it will have a y-axis
Step-by-step explanation:
Answer:
True.
Step-by-step explanation:
A horizontal line goes on infinitely on both ends will eventually cross the y-axis, making a y-intercept.
Assume that the following holds:
X + Y = Z
(a) Let X ~ N(0, 1) and Z~ N(0, 2). Find a Y such that (*) holds and specify the marginal distribution of Y as well as the joint distribution of X, Y and Z.
(b) Now instead let X N(0,2) and Z~ N(0, 1).
i. Show that X and Y are dependent.
ii. Find all a ЄR such that Y = aX is possible. Obtain the corresponding variance(s) of Y.
iii. What is the smallest Var(Y) can be?
iv. Find a joint distribution of X, Y and Z such that Y assumes the variance bound obtained in part biii above. Compute the determinant of the covariance matrix of the random vector (X, Y, Z).
Answers
(a) To satisfy (*) with X ~ N(0, 1) and Z ~ N(0, 2), we can rearrange the equation as follows: Y = Z - X. Since X and Z are normally distributed, their linear combination Y = Z - X is also normally distributed.
The mean of Y is the difference of the means of Z and X, which is 0 - 0 = 0. The variance of Y is the sum of the variances of Z and X, which is 2 + 1 = 3. Therefore, Y ~ N(0, 3). The joint distribution of X, Y, and Z is multivariate normal with means (0, 0, 0) and covariance matrix:
```
[ 1 -1 0 ]
[-1 3 -1 ]
[ 0 -1 2 ]
```
(b) i. To show that X and Y are dependent, we need to demonstrate that their covariance is not zero. Since Y = aX, the covariance Cov(X, Y) = Cov(X, aX) = a * Var(X) = a * 2 ≠ 0, where Var(X) = 2 is the variance of X. Therefore, X and Y are dependent.
ii. For Y = aX to hold, we require a ≠ 0. If a = 0, Y would always be zero regardless of the value of X. The variance of Y can be obtained by substituting Y = aX into the formula for the variance of a random variable:
Var(Y) = Var(aX) = a^2 * Var(X) = a^2 * 2
iii. The smallest variance that Y can have is 2, which is achieved when a = ±√2. This occurs when Y = ±√2X.
iv. To find the joint distribution of X, Y, and Z such that Y assumes the variance bound of 2, we can substitute Y = √2X into the covariance matrix from part (a). The resulting covariance matrix is:
```
[ 1 -√2 0 ]
[-√2 2 -√2]
[ 0 -√2 2 ]
```
The determinant of this covariance matrix is -1. Therefore, the determinant of the covariance matrix of the random vector (X, Y, Z) is -1.
Conclusion: In part (a), we found that Y follows a normal distribution with mean 0 and variance 3 when X ~ N(0, 1) and Z ~ N(0, 2). In part (b), we demonstrated that X and Y are dependent. We also determined that Y = aX is possible for any a ≠ 0 and found the corresponding variance of Y to be a^2 * 2. The smallest variance Y can have is 2, achieved when Y = ±√2X. We constructed a joint distribution of X, Y, and Z where Y assumes this minimum variance, resulting in a covariance matrix determinant of -1.
To know more about linear combination follow the link:
https://brainly.com/question/29393965
#SPJ11
40 students were surveyed about whether they have a cat, dog, or both. Event A = Cat Event, B= Dog.
( P and B) = 9/40
P(A)= 23/40
P(B)= 2/5
(A|B)=
A. 16/23
B. 9/40
C. 7/16
D. 9/16
Fill in the Digram

Answers
Answer:
C
Step-by-step explanation:
The area of this rectangle is at most 400 square centimeters. Write and solve an inequality to represent the
possible values for the height, h, for this triangle. Show all steps of your work
Answers
Answer:
1ft≤h≤25ft
Step-by-step explanation:
The area of a rectangle is expressed as;
Area = Length * height
A = Lh
If the area of a rectangle is at most 400 square centimeter, this is expressed as;
A ≤400
≤ means at most that is the area of the rectangle cannot be greater than 400
Substitute the given value into the inequality expression
Lh ≤ 400
Given
L = 16
16h ≤ 400
Divide both sides by 16
16h/16 ≤ 400/16
h ≤ 400/16
h ≤ 25
Hence the possible values of the height are with the range 1ft≤h≤25ft since we cannot have a negative value for the dimension
George bought nachos and two granola bars for $4.95. The nachos were $2.75. How much is one granola bar?
Answers
Answer:
$1.10
Step-by-step explanation:
4.95-2.75=2.20
2.20/2=1.10
Answer:
$1.10
Step-by-step explanation:
4.95-2.75=2.20
2.20÷2=1.10
What is the solution to log Subscript 5 Baseline (10 x minus 1) = log Subscript 5 Baseline (9 x + 7)
Answers
Answer:
x = 8Step-by-step explanation:
Given:
log₅ (10x - 1) = log₅ (9x + 7)10x - 1 = 9x + 710x - 9x = 7 + 1x = 8▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓
\(\sf{log_{5}}(\tt{10x-1})=\sf{log_{5}}(\tt{9x+7})\\\\10x-1=9x+7\\\\10x-9x=7+1\\\\\pmb{\green{\underline{\sf{x=\frak{8}}}}}\)
▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓
Number three please :))
Answers
Answer:
can u add a picture of what u want help with please
Step-by-step explanation:
Find the domain of the following vector-valued function.
r(t) = √1-t² i + √t j + (8/√7+t)k
Select the correct choice below and fill in any answer boxes within your choice.
A. {t: t≤ .... or t≥ ... }
B. {t: .... t ≤ t < ... }
C. {t: ....
D. {t: t< ... or t ≥ ...}
E. {t: t< .... or t> ....}
G. {t: ... ≤ t ≤ ....}
F. {t: ... < t< ....}
H. {t: t ≤ ... or t > ....}
Answers
The domain of the following vector-valued function is A.{t: t ≤ 0 or t ≥ 1} ∪ {t: t ≥ -7}
The given vector-valued function is: r(t) = √(1-t²) i + √t j + (8/√(7+t)) k We need to find the domain of this function. The domain of the function r(t) is the set of all possible values of t for which the function is defined and gives a real output. A vector-valued function is defined for all values of t that are in the domain of each component function of the vector.
The given function has three components:√(1-t²), √t, and (8/√(7+t)) The first two components are defined for t such that 1 - t² ≥ 0 and t ≥ 0, respectively. So, 0 ≤ t ≤ 1 satisfies both conditions. The third component is defined for t such that 7 + t > 0, which is equivalent to t > -7. Thus, the domain of the given function is: t ∈ [0, 1] or [-7, ∞).
To know more about function visit:-
https://brainly.com/question/31062578
#SPJ11
Reduce to simplest form. -9/12 - (-7/4)=
Answers
Answer:
answer is 1
Step-by-step explanation:
\(-\frac{9}{12} - (-\frac{7}{4}) = -\frac{3}{4} - (-\frac{7}{4})\\=\frac{4}{4} = 1\)
WILL GIVE BRAINLIEST!!!
If the measure of arc AB = 58 and the measure of arc CD = 18, what is the value of x? The figure is not drawn to scale.

Answers
The correct answer is option D. which is the angle x will be 38 degrees.
What is the angle of arc theorem?The measure of the angle created when two chords collide inside a circle is one-half the sum of the arcs intercepted by the angle and its vertical angle.
Here we have a measure of arc AB = 58 and the measure of arc CD = 18, So what is the value of x?
The value of x will be calculated by using the angle of arc theorem.
x = Sum of the arcs / 2
x = ( 58 + 18 ) / 2
x = ( 38 degrees )
Therefore the correct answer is option D. which is the angle x will be 38 degrees.
To know more about the angle of arcs theorem follow
https://brainly.com/question/3538263
#SPJ1
A regular hexagon is shown below.
If the length of each side of the hexagon is 30 cm, and the radius of the hexagon is also 30 cm, what is the hexagon's approximate area? Round your answer to the nearest tenth.
PLEASE DRAW IT OUT

Answers
Answer:
area = 2,338.2cm^2
Step-by-step explanation:
There is a simple formula for finding the area of a regular hexagon via its side length, but I'm assuming your teacher would like it geometrically considering you asked me to draw it out!
See attached image.
Find the height of the shaded triangle using the Pythagorean theorem:
15^2 + h^2 = 30^3
225 + h^2 = 900
h^2 = 675
h = ~25.98 cm
Find the area of the shaded triangle using 1/2bh:
1/2(15)(25.98) = 194.85
There are 12 such triangles in the hexagon.
12(194.85) = 2,338.2

Use the distributive property to simplify the following expression:
1/3 (9-6n)
Answers
Answer:
3 - 2n
Step-by-step explanation:
if you are sexually active, what are the odds of you contracting an sti by the time you are 25 years old?
Answers
The odds of you contracting an sti by the time you are 25 years old is 50%.
Even if a person has only had one physical relationship, that partner could be infected. Of course, the risks of contracting STDs (also known as sexually transmitted illnesses, or STIs) increase if a person has unprotected intercourse with a variety of partners.
Many persons with STDs have no evident indications or symptoms. As a result, individuals may assume they are "clean" and inform partners they don't need to use a protection.
But that's not a good idea. For example, almost six out of ten young people infected with HIV are unaware of their status. As a result, they risk infecting others with the AIDS virus.
To learn more about STI
brainly.com/question/27905312
#SPJ4
Given log3 4=1.262 and log3 7=1.771, what is the value of log3 (16/7)?
Answers
Answer:
Step-by-step explanation:
\(log \dfrac{a}{b}=log \ a - log \ b\\\\log \ a^{m}=m*log \ a\\\\\\log_{3} \ \dfrac{16}{7}=log_{3} \ 16 - log_{3} \ 7\\\\\\= log_{3} \ 4^{2} - log_{3} \ 7\\\\=2*log_{3} \ 4 - log_{3} \ 7\\\\= 2 * 1.262 - 1.771\\\\= 2.524 - 1.771\\\\= 0.753\)
If 8x + 6y = 24, what is y in terms of x ?
Answers
Step-by-step explanation:
8x+6y=24
6y=24-8x
y=24/6 - 8/6x
y=4-4/3x
What is 10 x 4 onss =_ ones =_____
Answers
\(\huge\text{Hey there!}\)
\(\textsf{If }\mathsf{10\times4 = \boxed{\star\ \bf {40\ }\star}}\textsf{, then that means you will have \bf 4 }\boxed{tens}\textsf{ \& \bf 0 \boxed{ones}\ }\large\checkmark\)
\(\mathsf{10 \rightarrow 1\ ten}\)
\(\mathsf{4\rightarrow 4 \ ones}\)
\(\mathsf{40\rightarrow 4\ tens\ \& \ 0 \ ones\ or\ simply\ 4\ tens\ }\large\checkmark\)
\(\huge\text{Good luck on your assignment \& enjoy your day!}\)
~\(\frak{Amphitrite1040:)}\)
Answer:
40
Step-by-step explanation:
Complete the given statement:
10x4 ones=____ ones =_____
Consider ones
Since 'ones' represents the place value of the units digit. So, the value of the place value 'ones' is 1.
= 10 times ( 4 ones)
= 10 times 4
= 40 ones
= 40
So, ones = 40 ones = 40.