Consider the sequence 5, 12, 19, 26, ... Enter numbers in the boxes to represent the fourth term as an ordered pair. ( , )
Answers
Answer:
(4,33)
Step-by-step explanation:
This is an arithmetic sequence with common difference of 7.
The fourth term = 26+7 = 33
Related Questions
I REALLY NEED SOME HELP PLSSS


Answers
The vocabulary term for segment a is an apothem.
The area of this polygon is 41.6 yd².
How to calculate the area of a regular polygon?In Mathematics and Geometry, the area of a regular polygon can be calculated by using this formula:
Area of regular polygon = (n × s × a)/2
Where:
n represents the number of sides.s represents the side length.a represents the apothem.By substituting the given parameters into the formula for the area of a regular polygon, we have the following:
Area of regular polygon = (6 × 4 × 2√3)/2
Area of regular polygon = (24 × 2√3)/2
Area of regular polygon = 83.1/2
Area of regular polygon = 41.6 yd².
Read more on regular polygon and apothem here: https://brainly.com/question/30970394
#SPJ1
A random sample of 84 students at a university showed an average age of 22 years and a sample standard deviation of 3 years. Find the margin of error for the 94% confidence interval. (Assume that the population of students is large relative to the sample size. Round your solution to 4 decimal places)
Answers
Answer:
The margin of error for the 94% confidence interval is 0.6154.
Step-by-step explanation:
The (1 - α)% confidence interval for population mean is:
\(CI=\bar x\pm z_{\alpha/2}\cdot\frac{\sigma}{\sqrt{n}}\)
The margin of error of this interval is:
\(MOE=z_{\alpha/2}\cdot\frac{\sigma}{\sqrt{n}}\)
The critical value of z for 94% confidence level is, z = 1.88.
Compute the margin of error for the 94% confidence interval as follows:
\(MOE=z_{\alpha/2}\cdot\frac{\sigma}{\sqrt{n}}\)
\(=1.88\times\frac{3}{\sqrt{84}}\\\\=0.6154\)
Thus, the margin of error for the 94% confidence interval is 0.6154.
A standard deck of playing cards contains 52 total cards, 13 of which are "spades".
Suppose you and a friend are playing a game. You can choose any two cards from the deck without looking. If the two cards you choose are both spades, you win!
You pull out one card, and then another, without putting the first one back.
What is the approximate probability that you win? Are your two choices independent or dependent events?
6%, Independent
6%, Dependent
11%, independent
11%, Dependent
Answers
The probability that you win is 6%, and the two choices are dependent events option (B) is correct.
What is probability?
It is defined as the ratio of the number of favorable outcomes to the total number of outcomes, in other words, the probability is the number that shows the happening of the event.
It is given that:
A standard deck of playing cards contains 52 total cards, 13 of which are "spades".
The probability of the first draw:
Probability = favorable outcomes/total outcomes
First draw: 1/4
For the second draw:
Second draw = 12/51
The probability that you win = (1/4)(12/51) = 3/51
In percent:
= (3/51)x100
= 5.88 = 6%
Thus, the probability that you win is 6%, and the two choices are dependent on events option (B) is correct.
Learn more about the probability here:
brainly.com/question/11234923
#SPJ1
what is the volume of the composite figure 16 7 3 5 3 6

Answers
The total volume of the composite figure is; 381 m³
How to find the volume of the composite figure?The formula for volume of a prism is;
V = Bh
where;
B is area of triangular base
h is height of prism
Thus;
V = (¹/₂ * 3 * 5) * 6
V = 45 m³
Volume of bottom cuboid is given by the formula;
V = Length * width * height
Thus;
V = 16 * 7 * 3
V = 336 m³
Total volume of composite figure = 45 m³ + 336 m³
Total volume of composite figure = 381 m³
Read more about Composite figure Volume at; https://brainly.com/question/13175744
#SPJ1
Consider the quadratic equation x2 + 2x - 35 = 0. Solve by factoring and using the zero-product property.
What are solutions to quadratic equations called? Show your work.
Answers
Answer:
x = -7
x = 5
Step-by-step explanation:
The standard form of quadratic equations is
Ax^2 + Bx + C = 0
The factors need to multiply together to be C and add together to be B.
The two numbers that will multiply together to be -35 and add together to be 2 are -5 & 7.
The factor pairs are (x+7)(x-5). Zero product property means we set each of those factor pairs = 0 and solve.
x + 7 = 0
-7 -7 Subtract 7 from each side to solve
x = -7
x - 5 = 0
+5 +5 Add 5 to each side to solve
x = 5
To solve the equation, factor x²+2x−35 use the formula x² +(a + b) x + ab = (x + a)(x + b). To find a and b, set up a system to be solved.
a + b = 2
ab = −35
Since ab is negative, a and b have opposite signs. Since a+b is positive, the positive number has a greater absolute value than the negative. Show all pairs of integers whose product is −35.
−1.35−5.7Calculate the sum of each pair.
−1 + 35 = 34−5 + 7 = 2The solution is the pair that gives sum 2.
a = −5b = 7Rewrite the factored expression (x + a)(x + b) with the values obtained.
(x − 5)(x + 7)To find solutions to equations, solve x−5=0 and x+7=0.
x = 5x = −7What are the solutions of quadratic equations called?The "solutions" of a Quadratic Equation are the values where the equation equals zero. They are also called "roots", or even "zeros".
ヘ( ^o^)ノ\(^_^ )If you want to learn more about mathematics, I share this link to complement your learning:
https://brainly.com/question/16413695h(x)=-4+16 find x when h(x)=48 Plz don't say it is incomplete

Answers
Answer:
x = -8
Step-by-step explanation:
When h(x) = 48, you can simply just plug it back into the first equation. Don't let the h(x) confuse you!
Think of it like saying y = -4x + 16, y = 48.
48 = - 4x + 16
32 = - 4x
8 = -x
Divide by -1 both sides.
-8 = x
Each month the Bureau of Labor Statistics reports the number of people (in thousands) employed in the United States by age. The accompanying frequency distribution shows the results for August 2011.
Age Frequency
16 to 19 4,794
20 to 24 13,273
25 to 34 30,789
35 to 44 30,021
45 to 54 32,798
55 and over 28,660
a) Construct a relative frequency distribution. What proportion of workers is between 20 and 24 years old?
b) Construct a cumulative relative frequency distribution. What proportion of workers is younger than 35 years old?
Answers
Answer:
Hence, the proportion of workers is younger than \(35\) years old is \(0.3481\)
Step-by-step explanation:
(a)
(b)
Younger workers than \(35\) years
\(P=\frac{<35}{\text{sum of function}}\)
\(\Rightarrow P=\frac{4794+13273+30789}{140335}\)
\(\Rightarrow P=\frac{48856}{140335}\)
\(\Rightarrow P=0.3481\)

For questions 3-4, use the graph of the polynomial function to find the factorization of the polynomial. Assume there is no constant term. 3

Answers
3. The factored polynomial is p(x) = (x - 1)(x - 5)
4. The factored polynomial is p(x) = (x + 3)²
What is a polynomial?A polynomial is a mathematical expression in which the power of the unknown is greater than or equal to 2.
3. To factorize the polynomial using the graph, we see that the polynomial cuts the x - axis at x = 1 and x = 5.
This implies that its factors are (x - 1) and (x - 5)
So, the factored polynomial is p(x) = (x - 1)(x - 5)
4. To factorize the polynomial using the graph, we see that the polynomial touches the x - axis at only one point x = -3. So,it has repeated roots
This implies that its factors are (x - (-3)) = (x + 3) twice
So, the factored polynomial is p(x) = (x + 3)²
Learn more about factorization of polynomial here:
brainly.com/question/30806486
#SPJ1
Each of 6 students reported the number of movies they saw in the past year. Here is what they reported. 14, 11, 15, 19, 12, 10 Send data to calculator Find the mean number of movies that the students saw. If necessary, round your answer to the nearest tenth. movies X Ś
Answers
The mean number of movies that the students saw is 13.5 (rounded to the nearest tenth).
To find the mean number of movies the students saw, you need to calculate the average of the given data. Here are the reported numbers of movies seen by the 6 students: 14, 11, 15, 19, 12, 10.
To calculate the mean, you sum up all the reported numbers and divide by the total number of students. In this case, the total number of students is 6.
So, let's calculate the mean:
(14 + 11 + 15 + 19 + 12 + 10) / 6 = 81 / 6 = 13.5
Therefore, the mean number of movies that the students saw is 13.5 (rounded to the nearest tenth).
for such more question on mean
https://brainly.com/question/14532771
#SPJ8
please help me with my online classwork!

Answers
Answer:
840 cm²---------------------------
There are two triangular faces with base of 16 cm and height of 15 cm and three rectangular faces.
Find the sum of areas of all five faces:
S = 2*(1/2)*16*15 + (17*2 + 16)*12 = 240 + 600 = 840HELP!!! please this is my last question for my paper

Answers
Answer:
\(\sqrt{2}\)
Step-by-step explanation:
We can use pytho theorem to find X because its a right triangle, so:
a^2 + b^2 = c^2
plug our numbers
1^2 + 1^2 = x^2
simplify
1+1 = x^2
2=x^2
answer = root2
A tennis shoes regularly sells for $20.00. The store advertises a 15% discount. What is the sale price of the necklace in dollars?
Answers
Answer:
Shoes with discount = $17
Necklace = Price * 0.85
Step-by-step explanation:
-If the tennis shoes store sells other things than shoes-
Shoes = $20.00
Discount = 15%
*Price expressed as a percentage*
Price without discount = 100%
Price after discount = 100% - 15%
Price after discount = 85%
*Normal price*
Price without discount = 20
Price after discount = 20 * 0.85
Price after discount = 17
An instructor gives an exam with sixteen questions. Students are allowed to choose any eleven to answer. (Hint: To answer the following questions, these examples may be helpful: Examples 9.5.4, 9.5.5, 9.5.6, and 9.5.7.) (a) How many different choices of eleven questions are there?
Answers
The number of different choices of eleven questions that a student can make on an exam with sixteen questions is 4,096.
This number can be calculated by the combination formula. The combination formula is used to calculate the number of combinations of a certain size that can be made from a larger set. In this case, the larger set is sixteen questions and the smaller set is eleven questions. The combination formula, written as C (n,r) is equal to n! / (r! (n-r)!), where n is the size of the larger set and r is the size of the smaller set. Applying this formula to the problem at hand, 16! / (11! (16-11)!), yields 4,096.
There are sixteen cards, and eleven of them must be chosen, so the number of different choices for eleven questions is 4,096.
Learn more about combination formula here:
https://brainly.com/question/3901018
#SPJ4
Help pleaseeee…
Referring to the figure, find the area of thetrapezoid shown.
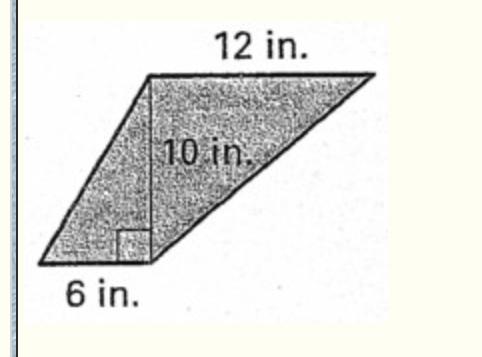
Answers
Answer:
Hello! answer: 90
Step-by-step explanation:
I split the trapezoid into 2 then did base × height ÷ by 2 cause the way I split it it made 2 triangles
10 × 12 = 120 10 × 6 = 60 120 + 60 = 180 180 ÷ 2 = 90 therefore 90 is our area Hope that HELPS!
Which is the correct pair?

Answers
Answer: D
Step-by-step explanation:
Since we are given that the x value is -1, we can eliminate A and C because the -1 is in the y coordinate.
To find the proper y value, we plug x into the equation.
y=-2x+5 [plug in x=-1]
y=-2(-1)+5 [multiply -2 and -1]
y=2+5 [add 2 and 5]
y=7
Now that we have the y value, we know the coordinate (-1,7) which makes D the correct answer.
I need help! 25 brainly points!

Answers
The surface areas for each figures are:
220 ft² 410 cm²596 cm²360 cm²Surface area of cylinders include: 132π mm²22π ft²396π square inches.How to calculate surface areas?1. The surface area of the cuboid is:
Top and bottom: 2(10 ft x 4 ft) = 80 ft²
Front and back: 2(10 ft x 5 ft) = 100 ft²
Sides: 2(4 ft x 5 ft) = 40 ft²
Total surface area = 80 + 100 + 40 = 220 ft²
2. The surface area of the cuboid is:
Top and bottom: 2(18 cm x 5 cm) = 180 cm²
Front and back: 2(18 cm x 5 cm) = 180 cm²
Sides: 2(5 cm x 5 cm) = 50 cm²
Total surface area = 180 + 180 + 50 = 410 cm²
3. The surface area of the prism is:
Top and bottom: 2(5 cm x 14 cm) = 140 cm²
Front and back: 2(5 cm x 12 cm) = 120 cm²
Sides: 2(12 cm x 14 cm) = 336 cm²
Total surface area = 140 + 120 + 336 = 596 cm²
4. The surface area of the stacked cuboids is:
Top and bottom of first cuboid: 2(6 cm x 7 cm) = 84 cm²
Front and back of first cuboid: 2(6 cm x 2 cm) = 12 cm²
Sides of first cuboid: 2(7 cm x 2 cm) = 28 cm²
Front and back of second cuboid: 2(7 cm x 2 cm) = 28 cm²
Sides of second cuboid: 2(2 cm x 4 cm) = 8 cm²
Front and back of third cuboid: 2(2 cm x 10 cm) = 40 cm²
Sides of third cuboid: 2(10 cm x 8 cm) = 160 cm²
Total surface area = 84 + 12 + 28 + 28 + 8 + 40 + 160 = 360 cm²
5. The surface area of the cylinder is:
Top and bottom: 2π(6 mm)² = 72π mm²
Side: 2π(6 mm)(5 mm) = 60π mm²
Total surface area = 72π + 60π = 132π mm²
6. The surface area of the cylinder is:
Top and bottom: 2π(1 ft)² = 2π ft²
Side: 2π(1 ft)(10 ft) = 20π ft²
Total surface area = 2π + 20π = 22π ft²
7. The surface area of the cylinder stacked on a cube is:
Top and bottom of cylinder: 2π(5 m)² = 50π m²
Side of cylinder: 2π(5 m)(8 m) = 80π m²
Surface area of cube: 6(10 m x 13 m) = 780 m²
Total surface area = 50π + 80π + 780 = (130π + 780) m²
8. The surface area of the cylinder is:
Top and bottom: 2π(9 in)² = 162π in²
Side: 2π(9 in)(4 in) = 72π in²
Therefore, the total surface area of the cylinder is:
2(162π in²) + 72π in² = 396π in²
So the surface area of the cylinder is 396π square inches.
Find out more on surface area here: https://brainly.com/question/16519513
#SPJ1
Image transcribed:
Find the surface area of each figure.
10 ft
18 cm
5 cm
4 ft
5 ft
3.
4.
6 cm
7 cm
2 cm
5 cm
12 cm
14 cm
4 cm
10 cm
8 cm
Find the surface area of each cylinder. Leave your answer in terms of π.
5.
6 mm
6.
1 ft
5 mm
10 ft
7.
5 m
8.
4 in.
8 m
10 m
9 in.
13 m
11 m
247
Journal and Practice Workbook
Geometry
What kind of geometric transformation is shown in the line of music?
•
reflection
translation
glide reflection

Answers
a glide reflection is a symmetry operation that consists of a reflection over a line and then translation along that line, combined into a single operation.
You can see the notes in this line of music translate or “glide” and “reflect” over the line
4n+2 (n+1) >n+52 Please solve this inequality fast.
Answers
Answer:
n>10.2 or n>51/5
Step-by-step explanation:
4n+2(n+1)>n+52 distribute 2 to everything in the parentheses
4n+2n+1>n+52 combine like terms
6n+1>n+52 subtract 1 from both sides
6n>n+51 subtract n from both sides
5n>51 divide both sides by 5
n>10.2
Answer:
n>10.2
Step-by-step explanation:
8x = 88
I can’t figure this out 10 points if you answer
Answers
Answer:
divide 88 by the number of x
88/8= 11
X = 11
Answer:
x=11
Step-by-step explanation:
8x=88
You use inverse operation which means you would divide 8 on both sides to isolate x on one side resulting in x=11
translate in terms of x then solve the algebra equation the sum of a number and 3 is subtracted from 10 the result is 5
Answers
Answer:
x=2
Step-by-step explanation:
10 - (x + 3) = 5
To solve for x, we can start by simplifying the left side of the equation:
10 - (x + 3) = 5
10 - x - 3 = 5
7 - x = 5
Next, we can isolate x on one side of the equation by subtracting 7 from both sides:
7 - x = 5
7 - x - 7 = 5 - 7
-x = -2
Finally, we can solve for x by dividing both sides of the equation by -1:
-x = -2
x = 2
Therefore, the solution to the equation is x = 2.
How many years will it take an initial investment of $25,000 to triple to $75,000 at an annual rate of 7% compounded continuously
Answers
Answer:
\(t = 15.7\)
Step-by-step explanation:
Given
\(Principal = 25000\) --- P
\(Amount = 75000\) --- A
\(Rate = 7\%\) --- R
Required
Determine the time (t)
Using continuous growth formula:
We have
\(A = Pe^{rt}\)
Convert rate to decimal
\(Rate = 7\%\)
\(r = 0.07\)
Substitute values for A, P and r
\(75000 = 25000 * e^{0.07t}\)
Divide both sides by 25000
\(3 = e^{0.07t}\)
Rewrite the exponential function as logarithmic, we have:
\(ln3 = 0.07t\)
Reorder
\(0.07t = ln3\)
Divide both sides by 0.07
\(t = \frac{ln3}{0.07}\)
\(t = \frac{1.09861228867}{0.07}\)
\(t = 15.69\)
\(t = 15.7\)
Hence, the time is approximately 15.7 years
Total population was 6,013 in 2018 and 5,175 in 2019.
What was the percent of change in population from 2018 to 2019?
Answers
Answer: : it is 4 over 8 and *
Step-by-step explanation:
Please help
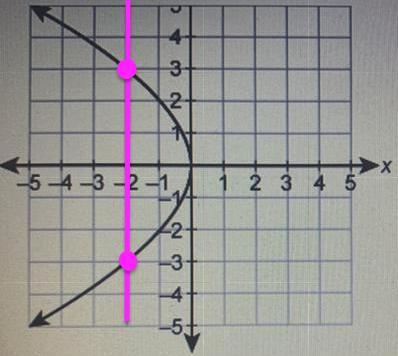
Answer the question in the picture
No links please

Answers
Answer:
The graph is NOT a function
Step-by-step explanation:
If I draw a vertical line everywhere on the graph, a vertical line must not touch two points. If You see how the graph curves on top off the bottom? Drawing a vertical line would hit two points
Consider the function below, which has a relative minimum located at (-3, -18) and a relative maximum located at 1/3, 14/27). f(x) = -x3 - 4x2 + 3x. Select all ordered pairs in the table which are located where the graph of f(x) is decreasing: Ordered pairs: (-1, -6), (2, -18), (0, 0),(1 , -2), (-3 , -18), (-4. , -12)
Answers
The ordered pairs (-1, -6), (2, -18), (0, 0), and (-4, -12) do not correspond to the intervals where the graph of f(x) is decreasing. The pairs (1, -2) and (-3, -18) are the correct ones.
To determine where the graph of f(x) is decreasing, we need to examine the intervals where the function's derivative is negative. The derivative of f(x) is given by f'(x) = -3x^2 - 8x + 3.
Now, let's evaluate f'(x) for each of the given x-values:
f'(-1) = -3(-1)^2 - 8(-1) + 3 = -3 + 8 + 3 = 8
f'(2) = -3(2)^2 - 8(2) + 3 = -12 - 16 + 3 = -25
f'(0) = -3(0)^2 - 8(0) + 3 = 3
f'(1) = -3(1)^2 - 8(1) + 3 = -3 - 8 + 3 = -8
f'(-3) = -3(-3)^2 - 8(-3) + 3 = -27 + 24 + 3 = 0
f'(-4) = -3(-4)^2 - 8(-4) + 3 = -48 + 32 + 3 = -13
From the values above, we can determine the intervals where f(x) is decreasing:
f(x) is decreasing for x in the interval (-∞, -3).
f(x) is decreasing for x in the interval (1, 2).
Now let's check the ordered pairs in the table:
(-1, -6): Not in a decreasing interval.
(2, -18): Not in a decreasing interval.
(0, 0): Not in a decreasing interval.
(1, -2): In a decreasing interval.
(-3, -18): In a decreasing interval.
(-4, -12): Not in a decreasing interval.
Therefore, the ordered pairs (-1, -6), (2, -18), (0, 0), and (-4, -12) are not located in the intervals where the graph of f(x) is decreasing. The correct answer is: (1, -2), (-3, -18).
For more question on intervals visit:
https://brainly.com/question/30460486
#SPJ8
Note the complete and the correct question is
Q- Consider the function below, which has a relative minimum located at (-3, -18) and a relative maximum located at 1/3, 14/27).
\(f(x) = -x^3 - 4x^2 + 3x\).
Select all ordered pairs in the table which are located where the graph of f(x) is decreasing: Ordered pairs: (-1, -6), (2, -18), (0, 0),(1 , -2), (-3 , -18), (-4. , -12)
How to use Pascal’s triangle to find x^2 using the difference quotient formula
Answers
Using Pascal's triangle and the difference quotient formula, we expand (x + h)^2 and simplify the expression to (2hx + h^2) / h. As h approaches 0, the term h becomes negligible, and we are left with 2x, which represents the derivative of x^2.
To use Pascal's triangle to find x^2 using the difference quotient formula, we can follow these steps:
1. Write the second row of Pascal's triangle: 1, 1.
2. Use the coefficients in the row as the binomial coefficients for (x + h)^2. In this case, we have (1x + 1h)^2.
3. Expand (x + h)^2 using the binomial theorem: x^2 + 2hx + h^2.
4. Apply the difference quotient formula: f(x + h) - f(x) / h.
5. Substitute the expanded expression into the formula: [(x + h)^2 - x^2] / h.
6. Simplify the numerator: (x^2 + 2hx + h^2 - x^2) / h.
7. Cancel out the x^2 terms in the numerator: (2hx + h^2) / h.
8. Divide both terms in the numerator by h: 2x + h.
9. As h approaches 0, the term h becomes negligible, and we are left with the derivative of x^2, which is 2x.
For more such questions on triangle
https://brainly.com/question/28470545
#SPJ8
what are two decimals that are equivalent to 2.200
Answers
Answer:
2.200 = 2.2 = 2.20 = 2.2000 = 2.20000...I could go on...
Step-by-step explanation:
Higher Order Thinking Morgan read
a thermometer at 7:00 P.M. The
temperature was 16°C. This temperature
was 9°C less than the temperature at
2:00 P.M. The temperature at 2:00 P.M.
was 10°C higher than the temperature at
8:00 A.M. What was the temperature at
8:00 A.M.?
Answers
The temperature at 8:00 A.M. was 15°C.
Using the given information:
1. At 7:00 P.M., the temperature was 16°C.
2. This temperature was 9°C less than the temperature at 2:00 P.M.
We can use this information to find the temperature at 2:00 P.M.:
Temperature at 2:00 P.M. = 16°C (temperature at 7:00 P.M.) + 9°C
Temperature at 2:00 P.M. = 25°C
3. The temperature at 2:00 P.M. was 10°C higher than the temperature at 8:00 A.M.
Now, we can find the temperature at 8:00 A.M.:
Temperature at 8:00 A.M. = 25°C (temperature at 2:00 P.M.) - 10°C
Temperature at 8:00 A.M. = 15°C
To know more about temperature refer to
https://brainly.com/question/24746268
8/5÷6=
i need help on this
Answers
Answer:
2 forms
Step-by-step explanation:
hope this helps <3

\( \sf \longrightarrow \: \frac{8}{5} \div 6 \\ \)
\( \sf \longrightarrow \: \frac{5}{8} \times 6 \\ \)
\( \sf \longrightarrow \: \frac{5 \times 6}{8} \\ \)
\( \sf \longrightarrow \: \frac{30}{8} \\ \)
\( \sf \longrightarrow \: \frac{8}{30} \\ \)
\( \sf \longrightarrow \: 0.26 \\ \)
_____________________________
The Red Shell's flight path is modeled by the equation:
y = -2x2 + 60x + 350
a) Factor the equation below:
olutions to the equation?
Answers
Answer:
Geometric figure: Straight Line
Slope = 120.000/2.000 = 60.000
x-intercept = 346/-60 = 173/-30 = -5.76667
y-intercept = 346/1 = 346.00000
Step-by-step explanation:
Rearrange:
Rearrange the equation by subtracting what is to the right of the equal sign from both sides of the equation :
y-(-4+60*x+350)=0
STEP
1
:
Equation of a Straight Line
1.1 Solve y-60x-346 = 0
Tiger recognizes that we have here an equation of a straight line. Such an equation is usually written y=mx+b ("y=mx+c" in the UK).
"y=mx+b" is the formula of a straight line drawn on Cartesian coordinate system in which "y" is the vertical axis and "x" the horizontal axis.
In this formula :
y tells us how far up the line goes
x tells us how far along
m is the Slope or Gradient i.e. how steep the line is
b is the Y-intercept i.e. where the line crosses the Y axis
The X and Y intercepts and the Slope are called the line properties. We shall now graph the line y-60x-346 = 0 and calculate its properties
Graph of a Straight Line :
Calculate the Y-Intercept :
Notice that when x = 0 the value of y is 346/1 so this line "cuts" the y axis at y=346.00000
y-intercept = 346/1 = 346.00000
Calculate the X-Intercept :
When y = 0 the value of x is 173/-30 Our line therefore "cuts" the x axis at x=-5.76667
x-intercept = 346/-60 = 173/-30 = -5.76667
Calculate the Slope :
Slope is defined as the change in y divided by the change in x. We note that for x=0, the value of y is 346.000 and for x=2.000, the value of y is 466.000. So, for a change of 2.000 in x (The change in x is sometimes referred to as "RUN") we get a change of 466.000 - 346.000 = 120.000 in y. (The change in y is sometimes referred to as "RISE" and the Slope is m = RISE / RUN)
Slope = 120.000/2.000 = 60.000
Geometric figure: Straight Line
Slope = 120.000/2.000 = 60.000
x-intercept = 346/-60 = 173/-30 = -5.76667
y-intercept = 346/1 = 346.00000
A bakery makes and sells hot cocoa bombs during the holidays. The first 12 hot cocoa bombs of an order cost is $4.00 each. Each of the next 6 hot cocoa bombs cost $3.50 each. For orders exceeding 18, the cost drops to $3 each. The function C(x) represents the bakery's pricing.

Answers
Solution
Step 1
Given data for C(x), the bakery's pricing
\(\begin{gathered} F\text{or this range 0}\leq x\leq12ofhotcocoabombs\text{ we use C(x) =4x} \\ \text{For this range }1218,ofhotcocoabombs\text{ we useC(x) = }3x+15 \end{gathered}\)Required
Step 1
To find the cost of 8 hot cocoa bombs
\(\begin{gathered} C(8)\text{ lies in the range 0}\leq x\leq12 \\ \text{Hence we use 4x where x = 8} \\ \text{The cost of 8 hot cocoa bombs = 4(8) = \$32} \end{gathered}\)Step 2
To find the cost of 18 hot cocoa bombs
\(\begin{gathered} C(18)\text{ lies in the range 12}Step 3To find the C(30)
\(\begin{gathered} C(30)\text{ lies in the range x}\ge18 \\ \text{Hence we use 3x +15, where x = 30} \\ C(30)\text{ = 3(30) + 15 = 90 + 15 = \$105} \\ \end{gathered}\)Step 4
What C(30) represents.
C(30) represents the cost of ordering 30 hot cocoa bombs which is $105