Consider the function represented by the graph. On a coordinate plane, a straight line with a negative slope begins on the y-axis at (0, 9) and exits the plane at (8, 1). What is the domain of this function?
Answers
Answer:
The domain of y = f(x) is [0,8]
Step-by-step explanation:
Since the straight line with negative slope begins on the y-axis at (0. 9) and exits the plane at (8, 1), we get is domain from the minimum and maximum values of x for which the function is valid.
So, the minimum value of x at which the function is valid is x = 0 and the function is y = f(0) = 9.The maximum value of x at which the function is valid is x = 8 and the function is y = f(8) = 1.
So, the domain of the function y = f(x) is [0,8]
Answer:
y = f(x) is [0,8]
Step-by-step explanation:
Related Questions
the director of research and development is testing a new drug. she wants to know if there is evidence at the 0.05 level that the drug stays in the system for more than 397 minutes. for a sample of 35 patients, the mean time the drug stayed in the system was 403 minutes. assume the population standard deviation is 18. find the p-value of the test statistic. round your answer to four decimal places.
Answers
By using the concept of mean and standard deviation, it can be inferred that
The the drug stays in the system for more than 397 minutes
What is mean and Standard Deviation?
Suppose there is a data set and the average of the data set has to be calculated. To calculate the average of the data set, mean is used
To know about Standard Deviation, it is important to know about Variance
Variance is the sum of the square of deviation from mean.
Square root of the variance gives the standard deviation
Given n = 35,
\(\bar{x} = 403,\)
Population mean \(\\ (\mu)\) = 397
Population Standard Deviation \(\\(\sigma)\) = 18
Here the sample size is large. So the distribution is approximately normal
To test :
\(H_ 0 = \mu \leq 397\\H_1 = \mu > 397\)
Test statistic t = \(\frac{403 - 397}{\frac{18}{\sqrt{35}}}\)
= 1.97
p value at \(\alpha = 0.05\) = 0.0244
Since 0.0244 < 0.05, the null hypothesis is rejected
So the the drug stays in the system for more than 397 minutes
To learn more about mean and Standard Deviation, refer to the link
https://brainly.com/question/28225633
#SPJ1
The amunt of money that college students spend on rent each month is usually between $300 and $600. However, there are a few students who spend $1,300. What measure of spread would be most appropriate to measure the amount of money that college student spend on rent per month? Explain in detail why or why not one of the below measures would be used.
A. Median
B. Range
C. Standard Deviation
D. Inquartile Range
Answers
The range would be the most appropriate measure of spread in this case because it takes into account the extreme values of $300 and $1,300 and provides a clear measure of the difference between them.
To measure the amount of money college students spend on rent per month, the most appropriate measure of spread would be the range. The range is the simplest measure of spread and is calculated by subtracting the lowest value from the highest value in a data set. In this case, the range would be $1,300 - $300 = $1,000.
The median would not be the best choice in this scenario because it only represents the middle value in a data set. It does not take into account extreme values like the $1,300 rent expense.
Standard deviation would not be the most appropriate measure of spread in this case because it calculates the average deviation of each data point from the mean. However, it may not accurately represent the spread when extreme values like the $1,300 rent expense are present.
The interquartile range (IQR) would not be the best choice either because it measures the spread of the middle 50% of the data set. It does not consider extreme values and would not accurately represent the range of rent expenses in this scenario.
In summary, the range would be the most appropriate measure of spread in this case because it takes into account the extreme values of $300 and $1,300 and provides a clear measure of the difference between them.
Know more about Standard deviation here,
https://brainly.com/question/29115611
#SPJ11
you have been transported to a jungle-scape in the body of a mathematician. you build a catapult to launch messages to your team, who are on the other side of a deep and wide revine. the graph below shows the trajectory of your message. you launch the message 7 feet east of a tree that is 5 feet west of the edge of the revine. the ravine is 12 feet wide.
Answers
The trajectory of your message illustrates a quadratic function
The equation of the trajectory of the message is \(y = -\frac 15(x - 17)^2 + 20\)
How to determine the equation of the graph?The trajectory graph (see attachment) is a quadratic function that passes through the following points:
(x,y) = (7,0) and (27,0)
And the vertex is:
(h,b) = (17,20)
A quadratic function is represented as:
\(y = a(x - h)^2 + b\)
So, we have:
\(y = a(x - 17)^2 + 20\)
Substitute (7,0) for (x,y)
\(0 = a(7 - 17)^2 + 20\)
Evaluate
\(0 = 100a + 20\)
Collect like terms
\(100a = -20\)
Divide both sides by 100
\(a = -\frac 15\)
Recall that:
\(y = a(x - 17)^2 + 20\)
So, we have:
\(y = -\frac 15(x - 17)^2 + 20\)
Hence, the equation of the trajectory of the message is \(y = -\frac 15(x - 17)^2 + 20\)
Read more about quadratic functions at:
https://brainly.com/question/4115477

Find the area of ΔLKJ

Answers
9514 1404 393
Answer:
D. 37.5 square units
Step-by-step explanation:
There are a couple of ways to figure this.
1. The altitude KM is the geometric mean of the segment lengths ML and MJ
KM = √(ML·MJ)
ML = KM²/MJ = 36/8 = 4.5
Then LJ = 4.5 +8 = 12.5, and the area of the triangle is ...
A = (1/2)bh
A = (1/2)(12.5)(6) = 37.5 . . . square units
__
2. Triangle LKM is similar to triangle KJM. The scale factor is ...
KM/JM = 6/8 = 3/4
Then the area of triangle LKM is (3/4)² = 9/16 of the area of triangle KJM.
The total area is ...
Area of LJK = (area of KJM)×(1 + 9/16)
= (1/2)(8)(6)(25/16) = 75/2 = 37.5 . . . square units
The side length of an equilateral triangle is 6x - 12. Write an expression for the perimeter of the triangle in simplest form.
Answers
Answer:
18x - 36
Step-by-step explanation:
In an equilateral triangle the 3 sides are congruent, then
perimeter = 6x - 12 + 6x - 12 + 6x - 12 ← collect like terms
= 18x - 36
The required expression would be 18x - 36 for the perimeter of the triangle in simplest form.
What is the perimeter of a triangle?The perimeter of a triangle is defined as the addition of the lengths of the triangle's three sides.
What are Arithmetic operations?Arithmetic operations can also be specified by adding, subtracting, dividing, and multiplying built-in functions. The operator that performs the arithmetic operations is called the arithmetic operator.
* Multiplication operation: Multiplies values on either side of the operator
For example 4*2 = 8
As we know in an equilateral triangle the 3 sides are congruent.
The perimeter of the triangle = 6x - 12 + 6x - 12 + 6x - 12
Combine the likewise terms and we get
The perimeter of the triangle = 18x - 36
Therefore, the required expression would be 18x - 36 for the perimeter of the triangle in simplest form.
Learn more about the perimeter of a triangle here:
brainly.com/question/24388271
#SPJ6
Can some one help me answer all ten questions they are due at 10:00 I will give out brainly. Part 2




Answers
Answer: go to quizlet it will most likely have the answers
Step-by-step explanation:
What method of assigning probabilities to a simple event uses relative frequencies?
Answers
The empirical method is the right answer.
Empirical probability is calculated by dividing the number of times an event was seen in your data by the entire sample size. An event's relative frequency is strongly connected to an empirical probability, also known as an experimental probability.
Empirical probability bases its estimation of the likelihood that a specific result will recur on the number of instances of that outcome within a sample set. In short, the empirical method uses relative frequencies to determine probabilities.
Here's another question with an answer similar to this about empirical method:
https://brainly.com/question/1452877
#SPJ4
mr mechoui is raising sheep. He has approximately 800 before going to bed he counts them by 10 by 12 and by 15 each time he finds the exact number. how many sheep does he have exactly ?
Answers
To find the answer, you need to check the multiples of 10, 12 and 15 and find the common multiple just below 800.
Polygon ABCD with vertices at A(−4, 6), B(−2, 2), C(4, −2), D(4, 4) is dilated using a scale factor of one half to create polygon A′B′C′D′. Determine the vertices of polygon A′B′C′D′.
Answers
The vertices of the dilated polygon A'B'C'D' are A'(-2, 3), B'(-1, 1), C'(2, -1), D'(2, 2).
What is the scale factor?
A scale factor is a number that represents the amount of magnification or reduction applied to an object, image, or geometrical shape.
To dilate a polygon by a scale factor of 1/2, each of its vertices needs to be multiplied by the factor of 1/2. This can be done by multiplying the x-coordinate and the y-coordinate of each vertex by 1/2.
So, for polygon ABCD, the coordinates of the dilated polygon A'B'C'D' can be found as follows:
Vertex A:
x-coordinate: -4 * 1/2 = -2
y-coordinate: 6 * 1/2 = 3
So, A' is located at (-2, 3).
Vertex B:
x-coordinate: -2 * 1/2 = -1
y-coordinate: 2 * 1/2 = 1
So, B' is located at (-1, 1).
Vertex C:
x-coordinate: 4 * 1/2 = 2
y-coordinate: -2 * 1/2 = -1
So, C' is located at (2, -1).
Vertex D:
x-coordinate: 4 * 1/2 = 2
y-coordinate: 4 * 1/2 = 2
So, D' is located at (2, 2).
Therefore, the vertices of the dilated polygon A'B'C'D' are:
A'(-2, 3), B'(-1, 1), C'(2, -1), D'(2, 2).
To know more about scale factors visit:
brainly.com/question/30314658
#SPJ1
write an equation of a line passing through the point (4,-9) and parallel to the line 3x-6y=30
Answers
The equation of a line in the slope intercept form is expressed as
y = mx + c
Where
m represents slope
c represents y intercept
The equation of the given line is expressed as
3x - 6y = 30
Rearranging it so that it will look like the slope intercept form, it becomes
6y = 3x - 30
Dividing both sides by 6, it becomes
6y/6 = 3x/6 - 30/6
y = x/2 - 5
Looking at the equation, slope, m = 1/2
If two lines are parallel, it means that they have equal slope. This means that the slope of the line parallel to the given line is 1/2
To determine the y intercept, c of the line passing through the point (4, - 9), we would substitute
x = 4, y = - 9 and m = 1/2 into the slope intercept equation. It becomes
- 9 = 1/2 * 4 + c
- 9 = 2 + c
c = - 9 - 2
c = - 11
By substtuting m = 1/2 and c = - 11 into the slope intercept equation, the equation of the line would be
y = x/2 - 11
A bucket contains 4 red balls and 5 orange balls. Two balls are pulled from the bucket, one after another, without replacement. Build a tree diagram showing the different possible outcomes for the two marbles being drawn. Be sure each branch is labeled with its individual probability and include the probability at the end of each branch.
Answers
Answer:
See the diagram below:
Red 3/8 -----------------> Red-Red = 4/9*3/8 = 1/6
Red 4/9 <
Orange 5/8 --------------> Red-Orange = 4/9*5/8 = 5/18
Red 4/8 --------------------> Orange-Red = 5/9*4/8 = 5/18
Orange 5/9 <
Orange 4/8 ----------------> Orange-Orange = 5/9*4/8 = 5/18
an airplane travels 1662 km Against The Wind in 3 hours and 2142 kilometers with the wind in the same are same amount of time what is the rate of the plane in still air and what is the rate of the Wind
Answers
Distance 1 = 1662 km
Time T= 3 hours
Distance 2= 2142 km
Time T=3 hours
Also
V1 = Plane velocity
V2= Air velocity
Then
Distance1/T = V1 - V2
and
Distance2/T= V1 + V2
1662/3= 554 = V1 - V2
2142/3= 706= V1 + V2
Now solve this 2x2 system, by substitution
then
V1= (554+ 706)/2= 1260/2= 630
V2= 706 - 630= 76
Then answer is
Velocity of plane= 630 km/h
Velocity of air= 76 km/h
What is the y-intercept of the line whose equation is y=−3x ?
Answers
Answer:
y=mx+b
b is the y intercept
b=0, so 0 is the y intercept
Step-by-step explanation:
Combine like terms to create an equivalent expression.
-2/3p + 1/5 + 5/6p
Answers
Answer:
1/6p + 1/5
Step-by-step explanation:
Hope this helps! Pls give brainliest!
5/6p-2/3p is the same as 5/6p-4/6p.
This will combine to form 1/6p.
So you are left with 1/5+1/6p
Or 1/6p+1/5
Since we are adding them together it doesn’t matter which one comes first.
Hope this helps!
The solution of the initial value problem dx/dt = 10x - 5y dy/dt = 8x - 12y x(0) = 2, y(0) = 1 is Select the correct answer. a. x = (35e^8t - e^10t)/18, y = (7e^8t + 2e^-1 d, x = (35e^8t - e^-10t)/9, y = (7e^8t - 2e^-10t b. x = (35e^8t + e^-10t)/18, y = (7e^8t + 2e^-1 e, x = (35e^8t - e^-10t)/18, y = (7e^8t - 2e^-1c. x = (35e^8t + e^-10t)/9, y = (7e^8t + 2e^-10t
Answers
The solution of the initial value problem dx/dt = 10x - 5y dy/dt = 8x - 12y x(0) = 2, y(0) = 1 is option (c) x = (35e^8t + e^(-10t))/18, y = (7e^8t + 2e^(-1)t).
To solve the given initial value problem, we need to find the values of x and y that satisfy the given differential equations and initial conditions.
We can start by solving the system of differential equations:
dx/dt = 10x - 5y
dy/dt = 8x - 12y
We can rearrange the first equation as follows:
dx/dt + 5y = 10x
This is a linear first-order differential equation, which we can solve using an integrating factor. The integrating factor is e^(∫5dt) = e^(5t), so we multiply both sides of the equation by e^(5t):
e^(5t)dx/dt + 5e^(5t)y = 10e^(5t)x
The left-hand side is the derivative of the product e^(5t)x with respect to t, so we can rewrite the equation as:
d/dt (e^(5t)x) = 10e^(5t)x
We can integrate both sides with respect to t to obtain:
e^(5t)x = (1/2)10e^(5t)^2 + C1
where C1 is a constant of integration. Simplifying the right-hand side, we get:
e^(5t)x = 5e^(10t) + C1
Dividing both sides by e^(5t), we get:
x = (5e^(5t) + C1e^(-5t))
Next, we can rearrange the second equation as follows:
dy/dt + 12y = 8x
This is another linear first-order differential equation, which we can solve using an integrating factor. The integrating factor is e^(∫12dt) = e^(12t), so we multiply both sides of the equation by e^(12t):
e^(12t)dy/dt + 12e^(12t)y = 8e^(12t)x
The left-hand side is the derivative of the product e^(12t)y with respect to t, so we can rewrite the equation as:
d/dt (e^(12t)y) = 8e^(12t)x
We can integrate both sides with respect to t to obtain:
e^(12t)y = (1/2)8e^(12t)^2 + C2
where C2 is a constant of integration. Simplifying the right-hand side, we get:
e^(12t)y = 4e^(24t) + C2
Dividing both sides by e^(12t), we get:
y = (4e^(12t) + C2e^(-12t))
Now we can use the initial conditions x(0) = 2 and y(0) = 1 to find the values of C1 and C2:
x(0) = 5(1) + C1(1) = 2
C1 = (2-5)/1*(-1) = 3
y(0) = 4(1) + C2(1) = 1
C2 = (1-4)/1*(-1) = 3
Substituting these values of C1 and C2 into the expressions we derived for x and y, we get:
x = (5e^(5t) + 3e^(-5t))
y = (4e^(12t) + 3e^(-12t))
Therefore, the correct option is (C) x = (35e^8t + e^(-10t))/18, y = (7e^8t + 2e^(-1)t).
Learn more about initial value problem here
brainly.com/question/30547172
#SPJ4
PLEASE HELP! 50 points!
In the graph, the area below f(x) is shaded and labeled A, the area below g(x) is shaded and labeled B, and the area where f(x) and g(x) have shading in common is labeled AB.
The graph represents which system of inequalities?
A. y ≤ −2x + 3
y ≤ x + 3
B. y ≥ −2x + 3
y ≥ x + 3
C. y ≤ −3x + 2
y ≤ −x + 2
D. y > −2x + 3
y > x + 3

Answers
Answer:
C. y ≤ −3x + 2 . Not sure, but I'm kind of confident in my answer.
how to determine the intercepts of the line with -5x+9y=-18
Answers
Answer:
-5x+9y=-18
Dividing both sides by -18
-5x/-18+9y/-18=-18/-18
5x/18-y/2=1
x/(18/5)-y/2=1. eqn(i)
eqn (i) is comparing with x/a+y/b=1, we get
x - intercept (a) =18/5
y-intercept (b) = -2
assume that for some statistic 1000 tests were performed. to avoid the situation of the incorrectly found significance, bonferroni correction was applied. the resulting p-value is 0.00013. what significance level was chosen for the tests? the significance level was:
Answers
The significance level chosen for the tests with total number of test performed as 1000 for given p-value is equal to 0.87 or 87%.
Total number of test performed = 1000
p-value is equal to 0.00013
The Bonferroni correction involves ,
Adjusting the significance level for multiple comparisons by dividing it by the number of comparisons performed.
Here, 1000 tests were performed and the resulting p-value is 0.00013.
The significance level that was chosen for the tests,
Reverse the Bonferroni correction by multiplying the p-value by the number of comparisons,
adjusted p-value = p-value / number of comparisons
number of comparisons = 1000
adjusted p-value = 0.00013
p-value = adjusted p-value x number of comparisons
⇒p-value = 0.00013 x 1000
⇒p-value = 0.13
So the original p-value before the Bonferroni correction was 0.13.
The significance level, we subtract the p-value from 1,
significance level = 1 - p-value
⇒significance level = 1 - 0.13
⇒significance level = 0.87
Therefore, the significance level chosen for the tests was 0.87 or 87%
learn more about significance level here
brainly.com/question/3487014
#SPJ4
what is the probability that at least seven customers arrive in three minutes, given that exactly two arrive in the first minute?
Answers
the probability that at least seven customers arrive in three minutes, given that exactly two arrive in the first minute, is approximately 0.081 or 8.1%.
How to solve?
To solve this problem, we can use the Poisson distribution, which models the probability of a certain number of events occurring in a fixed interval of time or space, given the expected rate of occurrence.
Let lambda be the expected rate of customer arrivals per minute. If exactly two customers arrive in the first minute, then the expected number of customers to arrive in three minutes is lambda ×3. We can use this expected value to calculate the probability of at least seven customers arriving in three minutes:
P(X ≥ 7 | X ~ ∝(λ×3))
= 1 - P(X ≤ 6 | X ~ ∝(λ×3))
= 1 - ∑[k=0 to 6] (e²(-λ3) ×(lλ3)²k / k!)
where e is the mathematical constant approximately equal to 2.71828, and k! denotes the factorial of k.
To find lambda, we can use the fact that exactly two customers arrive in the first minute. The Poisson distribution assumes that the number of events in a fixed interval of time or space follows a Poisson distribution with parameter lambda, which represents the expected rate of occurrence. Therefore, lambda is equal to the number of customers arriving per minute, which is 2.
Substituting lambda = 2 into the formula, we get:
P(X ≥ 7 | X ~ ∝(2×3))
= 1 - P(X ≤ 6 | X ~ ∝(6))
= 1 - ∑[k=0 to 6] (e²(-6) ×6²k / k!)
Using a calculator or computer software, we can evaluate this expression to get:
P(X ≥ 7 | X ~ ∝(6)) ≈ 0.081
Therefore, the probability that at least seven customers arrive in three minutes, given that exactly two arrive in the first minute, is approximately 0.081 or 8.1%.
To know more about Probability related question visit:
https://brainly.com/question/30034780
#SPJ1
Consider the interval of the form [a,b]∪(c,d). (a) Pick at least one integer and one rational number for a,b,c,d, making sure they make sense for this interval. Write your interval here: (b) Write the interval you came up with as an: - Inequality - Number line Write a sentence that explains the set of numbers (−[infinity],2)∪(2,[infinity])
Answers
(a) Interval: [1, 3] ∪ (1.5, 2.5)
(b) Inequality: 1 ≤ x ≤ 3 or 1.5 < x < 2.5
Number line:
```
1 1.5 2 2.5 3
----------------|-----------|-----------|-----------|---------------------
```
The interval [1, 3] ∪ (1.5, 2.5) consists of all real numbers greater than or equal to 1 and less than or equal to 3, including both endpoints, along with all real numbers greater than 1.5 and less than 2.5, excluding both endpoints.
In the inequality notation, 1 ≤ x ≤ 3 represents all numbers between 1 and 3, including 1 and 3 themselves. The inequality 1.5 < x < 2.5 represents all numbers between 1.5 and 2.5, excluding both 1.5 and 2.5.
On the number line, the interval is represented by a closed circle at 1 and 3, indicating that they are included, and an open circle at 1.5 and 2.5, indicating that they are not included in the interval. The line segments between the circles represent the interval itself, including all the real numbers within the specified range.
The interval [1, 3] ∪ (1.5, 2.5) includes all real numbers between 1 and 3, including 1 and 3 themselves, as well as all real numbers between 1.5 and 2.5, excluding both 1.5 and 2.5.
Learn more about real numbers : brainly.com/question/31715634
#SPJ11
calculate the range and standard deviation for 40, 65, 33, 46, 55, 50, 61
Answers
Answer:Therefore, the range is 32 and the standard deviation is approximately 10.523 for the given data set.
Step-by-step explanation:To calculate the range and standard deviation for the given data set {40, 65, 33, 46, 55, 50, 61}, we can follow these steps:
Step 1: Find the range.
The range is calculated by subtracting the minimum value from the maximum value in the data set.
Range = Maximum value - Minimum value
Range = 65 - 33
Range = 32
Step 2: Calculate the mean.
The mean is calculated by summing up all the values in the data set and dividing by the total number of values.
Mean = (40 + 65 + 33 + 46 + 55 + 50 + 61) / 7
Mean = 350 / 7
Mean = 50
Step 3: Calculate the deviation for each value.
Deviation is calculated by subtracting the mean from each value in the data set.
Deviation for 40 = 40 - 50 = -10
Deviation for 65 = 65 - 50 = 15
Deviation for 33 = 33 - 50 = -17
Deviation for 46 = 46 - 50 = -4
Deviation for 55 = 55 - 50 = 5
Deviation for 50 = 50 - 50 = 0
Deviation for 61 = 61 - 50 = 11
Step 4: Square each deviation.
Squared deviation for -10 = (-10)^2 = 100
Squared deviation for 15 = 15^2 = 225
Squared deviation for -17 = (-17)^2 = 289
Squared deviation for -4 = (-4)^2 = 16
Squared deviation for 5 = 5^2 = 25
Squared deviation for 0 = 0^2 = 0
Squared deviation for 11 = 11^2 = 121
Step 5: Calculate the variance.
Variance is calculated by summing up all the squared deviations and dividing by the total number of values.
Variance = (100 + 225 + 289 + 16 + 25 + 0 + 121) / 7
Variance = 776 / 7
Variance ≈ 110.857
Step 6: Calculate the standard deviation.
The standard deviation is the square root of the variance.
Standard Deviation ≈ √110.857
Standard Deviation ≈ 10.523
How to answer linear measure with mixed numbers problem
Answers
Answer:
1. Change the mixed number to an improper fraction; 1 1/2 as 3/1
2. Multiply both sides with the reciprocal of the improper fraction
3. Simplifly your answer if possible
Evaluate if k = 3.
k2 + 5 = [?]
Answers
Answer:
k=3 (3)x2+5=11
Hope this helps you and good luck :)
Step-by-step explanation:
pls solve plsssssssss

Answers
Answer:
D. It represents .90 cents, which is $5.40 divided by 6
Area of a rectangle playground in residential society is 2 2/5 square and one of its sides is 1 2/5 km find the length of other side
Answers
The length of the other side of the rectangle playground is 12/7 kilometers.
To find the length of the other side of the rectangle playground, we can use the formula for the area of a rectangle which is length multiplied by width.
Given that the area of the playground is 2 2/5 square kilometers, we can write this as a mixed number fraction:
2 2/5 = (5 x 2 + 2)/5 = 12/5
Let's assume that the side of the playground that we know the length of is the width. So, we have:
width = 1 2/5 km = (5 x 1 + 2)/5 km = 7/5 km
Now, we can substitute the area and width values into the formula for the area of a rectangle:
length x width = area
length x (7/5 km) = (12/5) km^2
Multiplying both sides by the reciprocal of 7/5, we get:
length = (12/5) km^2 ÷ (7/5) km
Simplifying, we get:
length = 12/7 km
To know more about rectangle visit:
https://brainly.com/question/15019502
#SPJ11
Let g(x) = cot(2).
Find g
(6)
Choose 1 answer:
2
B
0
-2
D
1

Answers
Answer:
C. -2
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
Brackets Parenthesis Exponents Multiplication Division Addition Subtraction Left to RightAlgebra I
Function NotationPre-Calculus
Unit CircleCalculus
DerivativesDerivative NotationDerivative of cot(x) = -csc²(x)Step-by-step explanation:
Step 1: Define
g(x) = cot(x)
g'(π/4) is x = π/4
Step 2: Differentiate
Differentiate: g'(x) = -csc²(x)Step 3: Evaluate
Substitute in x: g'(π/4) = -csc²(π/4)Evaluate: g'(π/4) = -2PLS I NEED HELLLPPPP
Find the value of x. Round to the nearest tenth. X 9 4 X = [ ? ]0
Answers
By calculating, The value of x from the given right angled triangle is 26.4
What is Tanx ?
Tanx can be defined as the ratio of sinx and cosx and it is also defined as the ratio of opposide side and hypothenuse in a given right angled triangle.
26.4° (nearest tenth)
sinx = opp/hyp
Put the given values opp = 4 and hyp=9
we get,
sinx = 4/9
x = sin^-1 ( 4/9)
So, by Taking the inverse of sine on both sides
we get,
x= 26.4° (nearest tenth)
Therefore, By calculating, The value of x from the given right angled triangle is 26.4
To learn more about Tanx from the given link.
https://brainly.com/question/13329070
#SPJ1
f(x, m, s) = 1 √278² exp (-2/2 (x-m) ²) 28² Write a function in the form of gauss(x, m=0, s=1) for computing the Gaussian density. Compute the Gaussian density for the following cases. (a) x=0, m=0, s-1. Give the name of question5a (b) x-2, m=0, s-1. Give the name of question5b (c) x-0, m-2, s-1. Give the name of question5e (d) x=0, m=2, s=2. Give the name of question5d (e) x=3, m-3, s-3.
Answers
Compute the Gaussian density for the following cases. (a) x=0, m=0, s-1. Give the name of question5a (b) x-2, m=0, s-1. The value of the account on January 1, 2021, would be $2,331.57.
To calculate the value of the account on January 1, 2021, we need to consider the compounding interest for each year.
First, we calculate the value of the initial deposit after three years (12 quarters) using the formula for compound interest:
Principal = $1,000
Rate of interest per period = 8% / 4 = 2% per quarter
Number of periods = 12 quarters
Value after three years = Principal * (1 + Rate of interest per period)^(Number of periods)
= $1,000 * (1 + 0.02)^12
≈ $1,166.41
Next, we calculate the value of the additional $1,000 deposit made on January 1, 2019, after two years (8 quarters):
Principal = $1,000
Rate of interest per period = 2% per quarter
Number of periods = 8 quarters
Value after two years = Principal * (1 + Rate of interest per period)^(Number of periods)
= $1,000 * (1 + 0.02)^8
≈ $1,165.16
Finally, we add the two values to find the total value of the account on January 1, 2021:
Total value = Value after three years + Value after two years
≈ $1,166.41 + $1,165.16
≈ $2,331.57
Therefore, the value of the account on January 1, 2021, is approximately $2,331.57.
Learn more about value here: brainly.com/question/9796766
#SPJ11
Find m angle 1 and m angle 2

Answers
Step-by-step explanation:
Firstly take the unknown angle be x
now x + 138° = 180° {: linear pair}
x = 180-138
x = 42
now , angle 1+ angle x + 18 = 180 { because of angle sum property }
=> angle 1 +42 +18 = 180
=> angle 1 +60 = 180
=> angle 1 = 180-60
=> angle 1 = 120

The orange figure below is a scale drawing of theblack figure. What is the scale factor, rounded tothe nearest whole number?
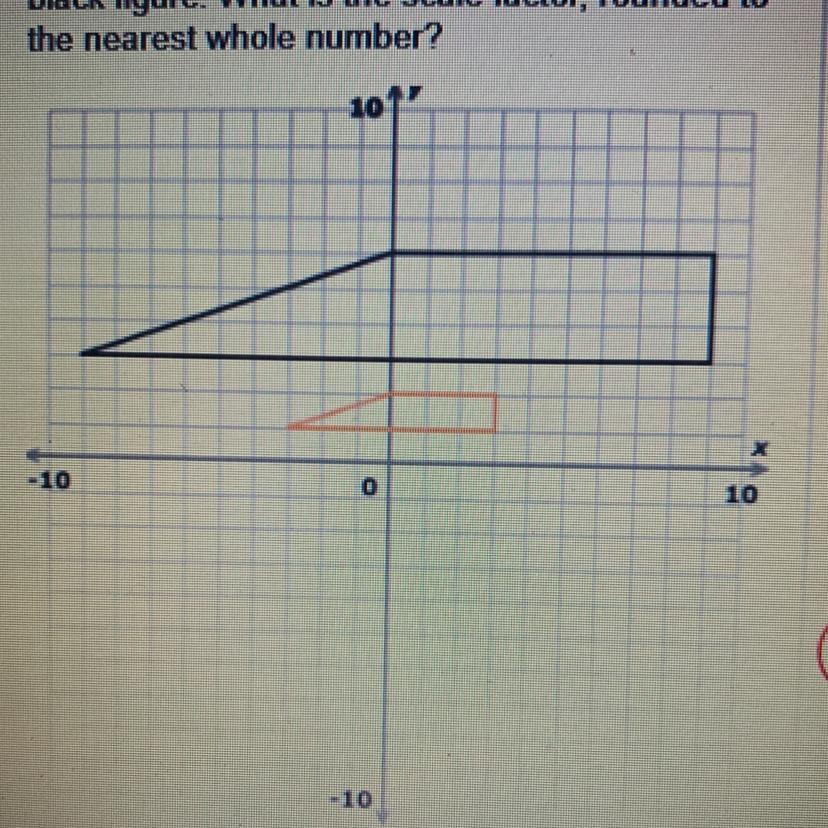
Answers
Scale factor is given by the formula below:
\(\text{Scale factor =}\frac{new\text{ length}}{\text{old length}}\)Using the right-hand side
new length = 1
old length= 3
substitute the values into the formular
\(\text{scale factors= }\frac{1}{3}=0.33333\approx0\)