Answers
Answer:
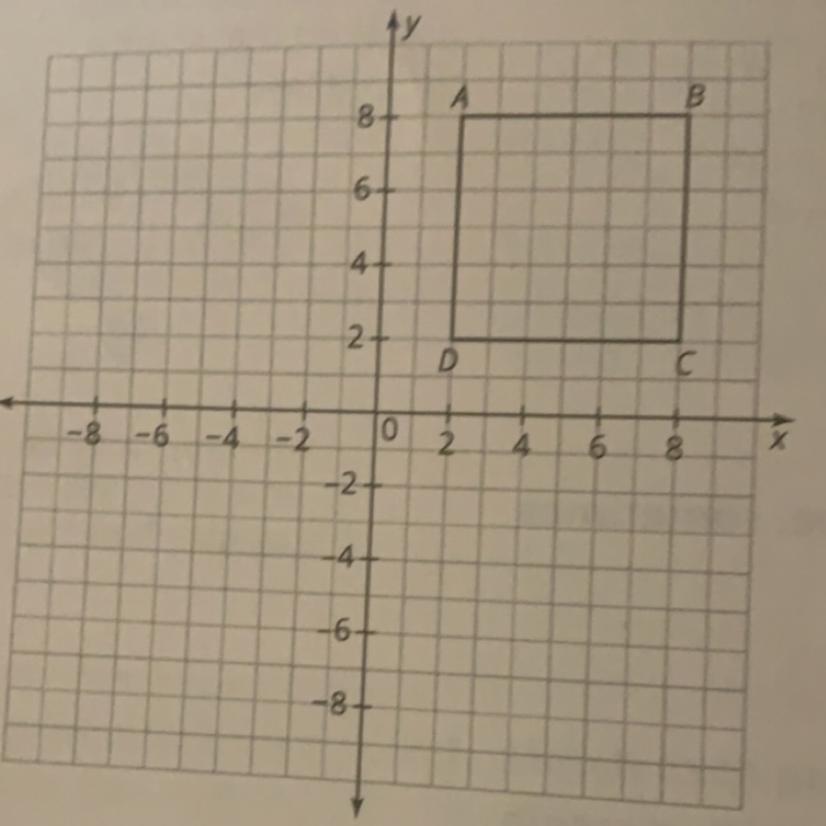
a=(2,8) b=(8,8)
c=(8,2) d=(2,2)
Step-by-step explanation:
Answer:
this quadrilateral would be a square because all of the sides are equal.
Related Questions
Compare the values of the following numbers, using the symbols > (greater than), < (less than), and = (equal to).
0.5 _____0.500
Answers
Answer:
0.5 = 0.500
Step-by-step explanation:
Both numbers are five-tenths. The zeros to the right of the 5 are not place holders and do not change the value of the number.
0.5 = 0.500
Heeeelp please, Can be zero or not?
with all steps and explanay.
Answers
The value of integral is 3.
Let's evaluate the integral over the positive half of the interval:
∫[0 to π] (cos(x) / √(4 + 3sin(x))) dx
Let u = 4 + 3sin(x), then du = 3cos(x) dx.
Substituting these expressions into the integral, we have:
∫[0 to π] (cos(x) / sqrt(4 + 3sin(x))) dx = ∫[0 to π] (1 / (3√u)) du
Using the power rule of integration, the integral becomes:
∫[0 to π] (1 / (3√u)) du = (2/3) . 2√u ∣[0 to π]
Evaluating the definite integral at the limits of integration:
(2/3)2√u ∣[0 to π] = (2/3) 2(√(4 + 3sin(π)) - √(4 + 3sin(0)))
(2/3) x 2(√(4) - √(4)) = (2/3) x 2(2 - 2) = (2/3) x 2(0) = 0
So, the value of integral is
= 3-0
= 3
Learn more about Definite integral here:
https://brainly.com/question/30760284
#SPJ1
Answer:
\(3-\displaystyle \int^{\pi}_{-\pi} \dfrac{\cos x}{\sqrt{4+3 \sin x}}\; \text{d}x\approx 0.806\; \sf (3\;d.p.)\)
Step-by-step explanation:
First, compute the indefinite integral:
\(\displaystyle \int \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x\)
To evaluate the indefinite integral, use the method of substitution.
\(\textsf{Let} \;\;u = 4 + 3 \sin x\)
Find du/dx and rewrite it so that dx is on its own:
\(\dfrac{\text{d}u}{\text{d}x}=3 \cos x \implies \text{d}x=\dfrac{1}{3 \cos x}\; \text{d}u\)
Rewrite the original integral in terms of u and du, and evaluate:
\(\begin{aligned}\displaystyle \int \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&=\int \dfrac{\cos x}{\sqrt{u}}\cdot \dfrac{1}{3 \cos x}\; \text{d}u\\\\&=\int \dfrac{1}{3\sqrt{u}}\; \text{d}u\\\\&=\int\dfrac{1}{3}u^{-\frac{1}{2}}\; \text{d}u\\\\&=\dfrac{1}{-\frac{1}{2}+1} \cdot \dfrac{1}{3}u^{-\frac{1}{2}+1}+C\\\\&=\dfrac{2}{3}\sqrt{u}+C\end{aligned}\)
Substitute back u = 4 + 3 sin x:
\(= \dfrac{2}{3}\sqrt{4+3\sin x}+C\)
Therefore:
\(\displaystyle \int \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x= \dfrac{2}{3}\sqrt{4+3\sin x}+C\)
To evaluate the definite integral, we must first determine any intervals within the given interval -π ≤ x ≤ π where the curve lies below the x-axis. This is because when we integrate a function that lies below the x-axis, it will give a negative area value.
Find the x-intercepts by setting the function to zero and solving for x in the given interval -π ≤ x ≤ π.
\(\begin{aligned}\dfrac{\cos x}{\sqrt{4+3\sin x}}&=0\\\\\cos x&=0\\\\x&=\arccos0\\\\\implies x&=-\dfrac{\pi }{2}, \dfrac{\pi }{2}\end{aligned}\)
Therefore, the curve of the function is:
Below the x-axis between -π and -π/2.Above the x-axis between -π/2 and π/2.Below the x-axis between π/2 and π.So to calculate the total area, we need to calculate the positive and negative areas separately and then add them together, remembering that if you integrate a function to find an area that lies below the x-axis, it will give a negative value.
Integrate the function between -π and -π/2.
As the area is below the x-axis, we need to negate the integral so that the resulting area is positive:
\(\begin{aligned}A_1=-\displaystyle \int^{-\frac{\pi}{2}}_{-\pi} \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&=- \left[\dfrac{2}{3}\sqrt{4+3\sin x}\right]^{-\frac{\pi}{2}}_{-\pi}\\\\&=-\dfrac{2}{3}\sqrt{4+3 \sin \left(-\frac{\pi}{2}\right)}+\dfrac{2}{3}\sqrt{4+3 \sin \left(-\pi\right)}\\\\&=-\dfrac{2}{3}\sqrt{4+3 (-1)}+\dfrac{2}{3}\sqrt{4+3 (0)}\\\\&=-\dfrac{2}{3}+\dfrac{4}{3}\\\\&=\dfrac{2}{3}\end{aligned}\)
Integrate the function between -π/2 and π/2:
\(\begin{aligned}A_2=\displaystyle \int^{\frac{\pi}{2}}_{-\frac{\pi}{2}} \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&= \left[\dfrac{2}{3}\sqrt{4+3\sin x}\right]^{\frac{\pi}{2}}_{-\frac{\pi}{2}}\\\\&=\dfrac{2}{3}\sqrt{4+3 \sin \left(\frac{\pi}{2}\right)}-\dfrac{2}{3}\sqrt{4+3 \sin \left(-\frac{\pi}{2}\right)}\\\\&=\dfrac{2}{3}\sqrt{4+3 (1)}-\dfrac{2}{3}\sqrt{4+3 (-1)}\\\\&=\dfrac{2\sqrt{7}}{3}-\dfrac{2}{3}\\\\&=\dfrac{2\sqrt{7}-2}{3}\end{aligned}\)
Integrate the function between π/2 and π.
As the area is below the x-axis, we need to negate the integral so that the resulting area is positive:
\(\begin{aligned}A_3=-\displaystyle \int^{\pi}_{\frac{\pi}{2}} \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&= -\left[\dfrac{2}{3}\sqrt{4+3\sin x}\right]^{\pi}_{\frac{\pi}{2}}\\\\&=-\dfrac{2}{3}\sqrt{4+3 \sin \left(\pi\right)}+\dfrac{2}{3}\sqrt{4+3 \sin \left(\frac{\pi}{2}\right)}\\\\&=-\dfrac{2}{3}\sqrt{4+3 (0)}+\dfrac{2}{3}\sqrt{4+3 (1)}\\\\&=-\dfrac{4}{3}+\dfrac{2\sqrt{7}}{3}\\\\&=\dfrac{2\sqrt{7}-4}{3}\end{aligned}\)
To evaluate the definite integral, sum A₁, A₂ and A₃:
\(\begin{aligned}\displaystyle \int^{\pi}_{-\pi} \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&=\dfrac{2}{3}+\dfrac{2\sqrt{7}-2}{3}+\dfrac{2\sqrt{7}-4}{3}\\\\&=\dfrac{2+2\sqrt{7}-2+2\sqrt{7}-4}{3}\\\\&=\dfrac{4\sqrt{7}-4}{3}\\\\ &\approx2.194\; \sf (3\;d.p.)\end{aligned}\)
Now we have evaluated the definite integral, we can subtract it from 3 to evaluate the given expression:
\(\begin{aligned}3-\displaystyle \int^{\pi}_{-\pi} \dfrac{\cos x}{\sqrt{4+3 \sin x}}\; \text{d}x&=3-\dfrac{4\sqrt{7}-4}{3}\\\\&=\dfrac{9}{3}-\dfrac{4\sqrt{7}-4}{3}\\\\&=\dfrac{9-(4\sqrt{7}-4)}{3}\\\\&=\dfrac{13-4\sqrt{7}}{3}\\\\&\approx 0.806\; \sf (3\;d.p.)\end{aligned}\)
Therefore, the given expression cannot be zero.
The quantity y varies directly with the square of x. If y=24 when x=3, find y when x is 4
Answers
Answer:
\(y = \frac{384}{9}\)
Step-by-step explanation:
Given
\(y\ \alpha\ x^2\) --- direct variation
\((x,y) = (3,24)\)
Required
y when x = 4
\(y\ \alpha\ x^2\)
Express as an equation
\(y = kx^2\)
Substitute: \((x,y) = (3,24)\)
\(24 = k*3^2\)
\(24 = k*9\)
Solve for k
\(k = \frac{24}{9}\)
To solve for y when x = 4, we have:
\(y = kx^2\)
\(y = \frac{24}{9} * 4^2\)
\(y = \frac{24}{9} * 16\)
\(y = \frac{24 * 16}{9}\)
\(y = \frac{384}{9}\)
A marketing firm conducts a survey to determine the ages of their survey subjects who like a new health drink.
This is the resulting data from their survey:
49, 63, 78, 22, 41, 39, 75, 61, 63, 65,
58. 37. 45, 52, 81, 75, 78, 72, 68, 59,
72, 85, 63, 61, 75, 39, 41, 48, 59,55
61, 25, 61, 52, 58, 71, 75, 82, 49, 51
The mean age of the subjects who like the new health drink is (type your answer...)
and the median age of the subjects is (type your answer..)
Answers
Answer:
Mean = 59.1, Median = 61
(there might have been a mistake in calculation (a lot of numbers!))
Step-by-step explanation:
The sample size is 40,
Now, the formula for the mean is,
Mean = (sum of the sample values)/(sample size)
so we get,
\(Mean = (49+63+78+22+41+39+75+61+63+65+58+37+45+52+81+75+78+72+68+59+72+85+63+61+75+39+41+48+59+55+61+25+61+52+58+71+75+82+49+51)/40\\Mean = 2364/40\\Mean = 59.1\)
To find the median, we have to sort the list in ascending (or descending)order,
we get the list,
22,25,37,39,39,41,41,45,48,49,
49,51,52, 52,55,58, 58, 59, 59, 61,
61, 61, 61, 63, 63, 63, 65, 68, 71, 72,
72, 75, 75, 75, 75, 78, 78, 81, 82, 85
Now, we have to find the median,
since there are 40 values, we divide by 2 to get, 40/2 = 20
now, to find the median, we takethe average of the values above and below this value,
\(Median = ((n/2+1)th \ value + (n/2)th \ value )/2\\where, \ the\ (n/2)th \ value \ is,\\n/2 = (total \ number \ of \ samples) /2\\n/2=40/2\\(n/2)th = 20\\Hence\ the (n/2)th \ value \ is \ the \ 20th \ value\)
And the (n+1)th value is the 21st value
Now,
The ((n/2)+1)th value is 61 and the nth value is 61, so the median is,
Median = (61+61)/2
Median = 61
A piece of lumber 2.8 meters long weighs 24.5 kilograms. A piece 0.8 meter long is cut from
the 2.8-meter length. Determine the weight of the 0.8-meter piece.
Answers
The weight of the 0.8-meter piece is 19.6 kilograms.
We can use the ratio of length to weight to determine the weight of the 0.8-meter piece.
Let's call the weight of the 2.8-meter piece "W₁" and the weight of the 0.8-meter piece "W₂". Then we have:
W₁/2.8m = 24.5kg/1m
Solving for W₁, we get:
W₁ = (24.5kg/1m) x 2.8m = 68.6kg
Now we can use the same ratio to find W₂:
W₂/0.8m = 24.5kg/1m
Solving for W₂, we get:
W₂ = (24.5kg/1m) x 0.8m = 19.6kg
Therefore, the weight of the 0.8-meter piece is 19.6 kilograms.
To learn more on Ratios click:
https://brainly.com/question/1504221
#SPJ1
PLEASE HELP
The table of values represents an exponential function.
What is the y-coordinate of -3f(x-1) when x = 0
Enter your answer in the box.
SEE PHOTO
Answers
The y-coordinate of -3f(x-1) when x = 0 is -63
What is the y-coordinate of -3f(x-1) when x = 0From the question, we have the following parameters that can be used in our computation:
The table of values
So, we have
-3f(x - 1)
When x = 0, we have
y = -3f(0 - 1)
This gives
y = -3f(-1)
From the table, we have
y = -3 * 21
Evaluate
y = -63
Hence, the y-coordinate is -63
Read more about exponential function at
https://brainly.com/question/2456547
#SPJ1
What is the area of a rectangle with a length of Four and two-fourths meters and a width of Seven and five-sixths meters?
Answers
Answer:
the area of the rectangle is 35.25 square meters.
Step-by-step explanation:
To find the area of a rectangle, we multiply the length by the width.
First, we need to convert the mixed numbers to improper fractions to make the multiplication easier:
4 and 2/4 = 4 + 2/4 = 16/4 + 2/4 = 18/4
7 and 5/6 = 7 + 5/6 = 42/6 + 5/6 = 47/6
Now we can multiply the length and width:
Area = (18/4) * (47/6)
Area = (9/2) * (47/6) (canceling the common factor of 2 between 18/4 and 6 in 47/6)
Area = (9 * 47) / (2 * 6)
Area = 423/12
Area = 35.25
Therefore, the area of the rectangle is 35.25 square meters.
if a=5, b=-2 and c=3 find the value of abc
Answers
Answer:
-30
Step-by-step explanation:
the order of multiplication doesn't matter
a*b*c = 5*-2*3 = -30
1. Brady had 432 Legos. Owen has
three times as many. How many Legos
does Owen have?
How
many do
they have all together?
Answers
A contact center provides incentives based on the number of sales achieved by its
representatives. Ross made 27 sales in 3 days. His colleague, Mona secured 49 sales in
one week. Who achieved a higher sales target per day?
HELP and please explain your thinking
Answers
Answer:
3 xhcni k ibohfpnconcfufuk
Which number sentence is true?
§ > }
Done →
Answers
A water tower 30 m tall is located at the top of a hill. From a distance of D = 125 m down the hill, it is observed that the angle formed between the top and base of the tower is 8°. Find the angle of inclination of the hill. Round your answer to the nearest tenth degree.
Answers
Answer:
the angle of inclination of the hill is 46.56°
Step-by-step explanation:
Given the data in the question;
Just as illustrated in the diagram below
so to find the angle of inclination of the hill;
sinA/30 = sinB/125
since angle BAC is 8°
we substitute
sin8°/30 = sinB/125
sinB = ( sin8°/30 ) × 125
B = sin⁻¹ ( ( sin8°/30 ) × 125 )
B = sin⁻¹ ( 0.004639 × 125 )
B = 35.44°
so since the some of a the angles of a triangle is 180;
A + B + C = 180
8° + 35.44° + C = 180
C = 180 - ( 8° + 35.44° )
C = 136.56°
Hence, Angle of inclination x will be;
x = 136.56° - 90°
x = 46.56°
Therefore, the angle of inclination of the hill is 46.56°
assuming equal population standard deviations for the two groups, give a 95% confidence interval for the
Answers
Answer: Give more info pls
Step-by-step explanation:
solve for h h and 26 is −52
Answers
Answer:
If you mean h multiplied by 26 is -52 then h is -2
If it is added to 26 then h is -78
If it is subtracted then h is -26
Step-by-step explanation:
Convert 0.45 to a percent. Remember to add the percent sign.
0.45%
4.5%
45%
50%
Answers
Answer:
45%
Step-by-step explanation:
a patient is advised to supplement her diet with 3g of calcium per day. The calcium tablets she purchases 300mg per tablet. How many tablets should the patient take per day?
Answers
Answer:
Number of tablet needed = 1 tablet
Step-by-step explanation:
Given:
Amount of calcium per day needed = 3 gram
Amount of calcium in a tablet = 300 mg
Find:
Number of tablet needed
Computation:
Number of tablet needed = Amount of calcium per day needed / Amount of calcium in a tablet
Number of tablet needed = 3gram / 300 milligram
Number of tablet needed = 300 milligram / 300 milligram
Number of tablet needed = 1 tablet
Plot the points on your graph paper to answer the question.
Are the paired points in a proportional relationship?
Drag and drop the correct answer into the box.
The paired points Response area in a proportional relationship.
x 0 1 2 3 4
y 0 3 6 9 12
Answers
Answer:
The answer is "are".
Step-by-step explanation:
I know this because i just took the quiz nd got a 100% so if you need anymore help you can ask me!
if lin has already run 19.6 miles of the marathon how many miles does she have left
Answers
Answer:
6.6 miles she has to runStep-by-step explanation:
the marathon actual race distance is 26.2 now that Lin has already ran 19.6 miles so now we should subtract this two decimal numbers so that were get 6.6
There are 54 girls on the playground. There are 25 fewer boys than girls on the playground. How many kids are on the playground?
Answers
Answer:
83 kids total
Step-by-step explanation:
There are 54 girls on the playground. There are 25 fewer boys than girls on the playground. How many kids are on the playground?
girls = 54
boys = 54 - 25 = 29
54 + 29 = 83 kids total
kids that are on the playground are 83.
What is the sum?Merging objects and identifying them since one big bunch is done through addition. In arithmetic, addition is the technique of adding two or more integers together. The product can meet are the quantities that are included, and the outcome of the operation, or the final response, is referred to as the sum.
The total number of girls that are present is 54
The data given is that there are
25 fewer boys taht are4 present
The total number of boys will be
boys = 54 - 25 = 29
The number of kids that are present will be the total of boys and girls that are present.
Kids = boys + girls
54 + 29 = 83 kids total
The quantity of kids that are present in the playground is 83.
Learn more about sum, here:
https://brainly.com/question/537797
#SPJ2
31 is what percent of 37?
Answers
Answer: The total answers count 37 - it's 100%, so we to get a 1% value, divide 37 by 100 to get 0.37. Next- calculate the percentage of 31: divide 31 by 1% value (0.37), and you get 83.78% - it's your percentage grade.
whats the whole number of 222+2022+2202+2220
Answers
Answer:
6666
Step-by-step explanation:
222+2022+2202+2220=6666
Colin pays £766.45 a year on his car insurance.
The insurance company increases the price by 5.4%.
How much does the insurance cost now?
Give your answer rounded to 2 DP.
Answers
=766.45x(1+0.054)
=766.45x1.054
= 807.8383
=807.84
Two student clubs were selling t-shirts and school notebooks to raise money for an upcoming school event. In the first few minut
notebooks, and made $19. Club B sold 1 t-shirt and 1 notebook, for a total of $8.
-
Use matrices to solve the equation and determine the cost of a t-shirt and the cost of a notebook. Show or explain all necessary:
Answers
Using matrices the simultaneous equation is solved to get x = 3 and y = 5
How to solve the simultaneous equation using matricesThis method required finding determinants in three occasions then dividing
The given equation
\(\left[\begin{array}{cc}3&2&\\1&1\\\end{array}\right] \left[\begin{array}{c}x\\y\\\end{array}\right]= \left[\begin{array}{c}19\\8\\\end{array}\right]\)
the determinant is
\(\left[\begin{array}{cc}3&2&\\1&1\\\end{array}\right]\)
3 * 1 - 2 * 1 = 3 - 2 = 1
Solving for x
determinant while replacing x values
\(\left[\begin{array}{cc}19&2&\\8&1\\\end{array}\right]\)
19 * 1 - 2 * 8 = 19 - 16 = 3
solving for x = 3/1 = 3
Solving for y
determinant while replacing y values
\(\left[\begin{array}{cc}3&19&\\1&8\\\end{array}\right]\)
3 * 8 - 19 * 1 = 24 - 19 = 5
solving for y = 5/1 = 5
Learn more about simultaneous equations at:
https://brainly.com/question/148035
#SPJ1
What is the solution to 4 x + 6 less-than-or-equal-to 18?
Answers
Answer:
a
Step-by-step explanation:
edge 2020-2021 <3333
(have an amazing day lovely)
cost of a sweater is 3395 markup is 70% what is the original price
Answers
Since we have that 3395 represent the 70% of the total, we now want to know how much the 100% is, for that we do as follows:
First we multiply the total ammount we are given ($3395) times the percentage we want to know (100%) and divide by the percentage we are given (70%):
\(x=\frac{3395\cdot100}{60}\Rightarrow x=4850\)x represents the original cost.
Originally since we have:
\(70->3395\text{ \& 100 }->x\)Now we need to solve for x, and since we have that when 70 represents 3395, then, how much does 100 represent?
For that we multiply the percentage we want to know (100%) times the total ammount we are given ($3395) and divide by the percentage we are given that represents the total ammount (70%):
\(x=\frac{100\cdot3395}{70}=>x=4850\)The basics go more or less like this:
If "a" represents "b", then "c" represents "d", is called "The rule of three", and with it you know that with 3 values you can infer the fourth on, as long as they are related in some way.
In the case of your problem, an ammount of money is represented by a percenage, and there is another percentage that is going to represent another ammount of money that we don't know. So we use this relationship to determine the ammount of money that the given percentage is representing.
\(a->b\text{ \& c}-d\)Now if we have a, b & c, we can calculate d:
\(d=\frac{c\cdot b}{a}\)And in the same fashion, as long as we have another set of 3 values we can determine the value of the fourth.
Use an induction proof to prove this statement:
For n≥1, 4^n+5 is divisible by 3.
Answers
Answer:
See below
Step-by-step explanation:
We shall prove that for all \(n\in\mathbb{N},3|(4^n+5)\). This tells us that 3 divides 4^n+5 with a remainder of zero.
If we let \(n=1\), then we have \(4^{1}+5=9\), and evidently, \(9|3\).
Assume that \(4^n+5\) is divisible by \(3\) for \(n=k, k\in\mathbb{N}\). Then, by this assumption, \(3|(4^n+5)\Rightarrow4^k+5=3m,\: m\in\mathbb{Z}\).
Now, let \(n=k+1\). Then:
\(4^{k+1}+5=4^k\cdot4+5\\=4^k(3+1)+5\\=3\cdot4^k+4^k+5\\=3\cdot4^k+3m\\=3(4^k+m)\)
Since \(3|(4^k+m)\), we may conclude, by the axiom of induction, that the property holds for all \(n\in\mathbb{N}\).
What is 8 x 7/8 in a fraction
Answers
Answer:
7/8 x 8 = 56/8 as simplified as 7/1 in fraction form.
Step-by-step explanation:
Hope it helps :)
Question
The Portland Trail Blazers won 41 games in the by the end of the 2017 season and 49 games by the end of the 201
season. Calculate the absolute and relative change in number of games won from the 2017 season to the 2018 se
Round your answer for relative change to the nearest hundredth of a percent.
Do not round until your final answer.
Provide your answer below:
Absolute Changes
Relative Change - %,
Answers
Answer: The absolute change in the number of games won from the 2017 season to the 2018 season is 49 - 41 = 8 games.
To calculate the relative change in the number of games won, we can use the formula:
Relative Change = ((New Value - Old Value) / Old Value) * 100
Plugging in the given values:
Relative Change = ((49 - 41) / 41) * 100 = (8 / 41) * 100 = 19.51 %
Round up to the nearest hundredth of a percent, The relative change is 19.51%.
So the absolute change in number of games won from the 2017 season to the 2018 season is 8 and relative change is 19.51%
Step-by-step explanation:
A tank in the shape of a hemisphere has a diameter of 24 feet. If the liquid that fills the tank has a density of 92.5 pounds per cubic foot, what is the total weight of the liquid in the tank, to the nearest full pound?
Answers
The total weight of the liquid in the tank is approximately 12,628 pounds.
To calculate the weight of the liquid, we need to determine the volume of the hemisphere and then multiply it by the density of the liquid. The formula for the volume of a hemisphere is V = (2/3)πr³, where r is the radius of the hemisphere.
In this case, the diameter of the tank is given as 24 feet, so the radius is half of that, which is 12 feet. Plugging this value into the formula, we get V = (2/3)π(12)³ ≈ 904.78 cubic feet.
Finally, we multiply the volume by the density of the liquid: 904.78 cubic feet * 92.5 pounds per cubic foot ≈ 12,628 pounds. Therefore, the total weight of the liquid in the tank is approximately 12,628 pounds.
In summary, to calculate the weight of the liquid in the tank, we first determine the volume of the hemisphere using the formula V = (2/3)πr³. Then, we multiply the volume by the density of the liquid.
By substituting the given diameter of 24 feet and using the appropriate conversions, we find that the total weight of the liquid is approximately 12,628 pounds.
for such more questions on weight
https://brainly.com/question/29892643
#SPJ8
Andy buys a rectangular rug that is 92 centimeters long and 80 centimeters wide. What is the area of the rug?
Answers
Answer:
7360² cm.
Step-by-step explanation:
area=length(width)