Consider a geometric sequence with a first term of 4 and a fourth term of -2.916.
a) Find the common ratio of this sequence.
b) Find the sum to infinity of this sequence.
Answers
Answer:
a) Find the common ratio of this sequence.
Answer: -0.82
b) Find the sum to infinity of this sequence.
Answer: 2.2
Step-by-step explanation:
nth term in geometric series is given by \(4\ th \ term = ar^n-1\\-2.196 = 4r^{4-1} \\-2.196/4 = r^{3} \\r = \sqrt[3]{0.549} \\r = 0.82\)
where
a is the first term
r is the common ratio and
n is the nth term
_________________________________
given
a = 4
4th term = -2.196
let
common ratio of this sequence. be r
\(4\ th \ term = ar^n-1\\-2.196 = 4r^{4-1} \\-2.196/4 = r^{3} \\r = \sqrt[3]{-0.549} \\r = -0.82\)
a) Find the common ratio of this sequence.
answer: -0.82
sum of infinity of geometric sequence is given by = a/(1-r)
thus,
sum to infinity of this sequence = 4/(1-(-0.82) = 4/1.82 = 2.2
Related Questions
Determine P(c) using the remainder theorem.. (look at image)
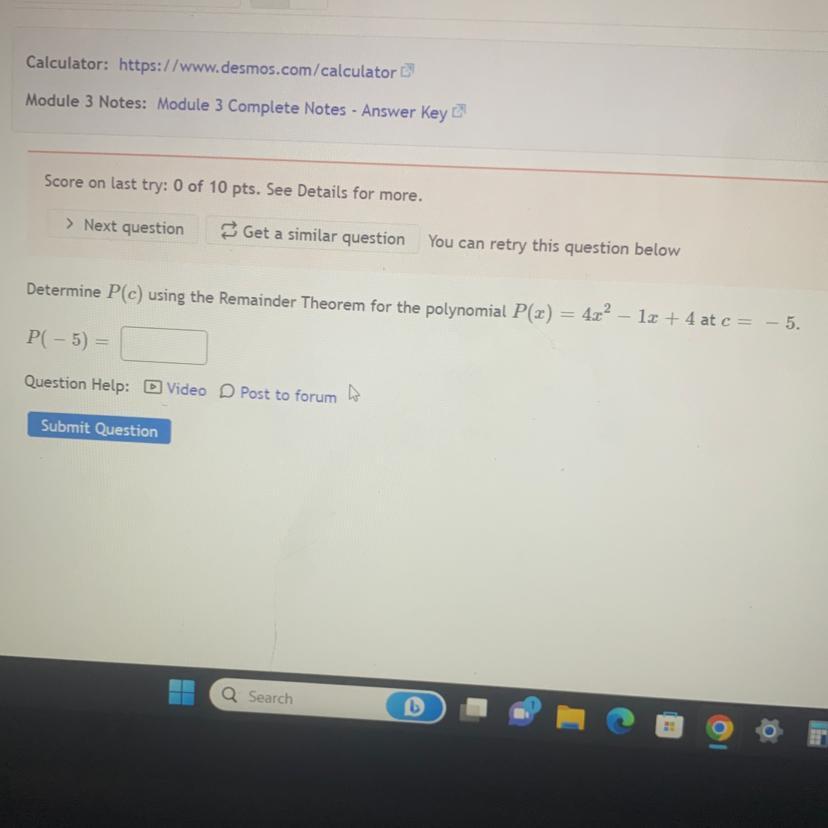
Answers
Answer:
P(-5) = 109
Step-by-step explanation:
Remainder theorem:If the polynomial p(x) is divided by the linear polynomial (x-a), the remainder is p(a).
Dividend = divisor * quotient + remainder.
p(x) = (x-a) * q(x) + p(a)
Here, q(x) is the quotient and p(a) is the remainder.
P(x) = 4x² - x + 4
P(-5) = 4*(-5)² - 1*(-5) + 4
= 4*25 + 5 + 4
= 100 + 5 + 4
= 109
Terms from two sequences are given in tables below. Which of the following statements are true? Select all that apply.

Answers
As per the terms from the two sequences given in tables as attachment hereby along with the question statement, the following statements from the provided options are true.
(i) [(a₁) > (g₂)]
(iv) Initially (aₙ) is greater than (gₙ), and as "n" gets larger, (gₙ) is greater than (aₙ).
As per the question statement and the reference tables attached thereby along with the question, we are provided with terms from the two sequences in table format, and five statements based on the sequences.
We are required to determine which statements among the five, are true.
To solve this question, we will use the trial-and-error method, where we will consider individual statement and assess it's honesty.
First statement is [(a₁) > (g₂)], which is true. As we can see from the table, that, [(a₁) = 10] and [(g₂) = 4], i.e., (10 > 4), or, [(a₁) > (g₂)].
Second statement is that, "The constant difference for (aₙ) is 10" which is False. We can clearly see from the table that, (a₁ = 10), (a₂ = 15), (a₃ = 20), (a₄ = 25) and so on, and [(25 - 20) = (20 - 15) = (15 - 10) = 5], i.e.,
[(a₄ - a₃) = (a₃ - a₂) = (a₂ - a₁) = 5]. Hence, the common difference for (aₙ) is 5, and not 10.
Third statement is that, "(aₙ) can be modelled by a linear function, and (gₙ) can be modelled by an exponential function" which is true for the first part, but false for the second, making the complete statement false as whole.
From the left hand side table, we can see that, (a₂ = 15) and (a₁ = 10),
Or, [a₂ = (10 + 5)]
Or, [a₂ = (a₁ + 5)]
Similarly, (a₃ = 20),
Or, [a₃ = (15 + 5)]
Or, [a₃ = (a₂ + 5)]
That is, we can generalise (aₙ) as
[aₙ = {(aₙ₋₁) + 5}] where, (n = 2, 3, 4, 5...) and (a₁ = 10).
Hence, (aₙ) can be modelled by a linear function.
But from the right hand side table, we can see that, (g₂ = 4) and (g₁ = 2),
Or, [g₂ = (2 * 2)]
Or, [g₂ = 2g₁]
Similarly, (g₃ = 8),
Or, [g3 = (2 * 4)]
Or, [g₃ = 2g₂], it goes on for (gₙ).
Therefore, we can generalise (gₙ) as
[gₙ = 2*(gₙ₋₁)] where, (n = 2, 3, 4, 5...) and (g₁ = 2).
Here, (gₙ) can also modelled as a linear function and not as a exponential function (which goes in the form of "xⁿ").
Coming to the fourth statement, "Initially (aₙ) is greater than (gₙ), and as "n" gets larger, (gₙ) is greater than (aₙ)" is true, as from both the tables,
For (n = 5), [aₙ = a₅ = (a₄ + 5) = (25 + 5) = 30],
And [gₙ = g₅ = (2 * g₄) = (2 * 16) = 32], which is greater than 30,
Or, [(g₅) > (a₅)].
Similarly, for (n = 6), (a₆ = 35) while (g₆ = 64), i.e., [(g₆) > (a₆)], and it continues for greater values of "n".
Coming to the last statement, that [a₁₀ > g₆], is false. As we can observe from the both the tables and their sequence,
For (n = 5), (aₙ = 50), for (n = 6), (aₙ = 35), for (n = 7), (aₙ = 40), for (n = 8), (aₙ = 45), for (n = 9), (aₙ = 50) and for (n = 10), (aₙ = 55),
While on the other hand, for (n = 5), (gₙ = 32) and for (n = 6), (gₙ = 64).
Since (64 > 55), therefore, [(g₆) > (a₁₀)].
Sequence: In mathematics, a sequence is an enumerated collection of objects in a particular order, and repetitions being allowed.To learn more about Sequence, click on the link below.
https://brainly.com/question/21961097
#SPJ1
If the circumference of a circle is 25.12 ft, find the radius. You must show all work to get full credit. Don't forget to label your answer.
Answers
Answer:
Radius ≈ 4
Step-by-step explanation:
The formula for circumference is 2 π r.
25.12 = 2 (3.14) r
25.12 = 2 (3.14) r
25.12 = (6.28) r
25.12 / 6.28 ≈ r
4 = r
A
B
C
D
19.86 m
23.78 m
16.31 m
39.42 m

Answers
The measure of the side 'x' is 16.31 m. The correct option is C.
Trigonometry is a branch of mathematics that deals with the study of the relationships between the sides and angles of triangles. It is a fundamental part of geometry that has many practical applications in fields such as physics, engineering, navigation, and surveying.
Given that in a right-angled triangle, the value of side RS is x, angle R is 25° and the side RT is 18 m.
The value of x will be calculated as,
sin65° = x / 18
x = 18 x sin65°
x = 16.31 m
Hence, the correct option is C.
To know more about trigonometry follow
https://brainly.com/question/31613548
#SPJ1
X Find the length and width of a rectangle whose width is 10 cm shorter
than its length and whose area is 200 cm squared. What is the SUM of
the length and width?
Answers
Answer:30
Step-by-step explanation: length is 20, Width is 20-10 =10
Area = 20×10=200
Rosanne is making a swirled pudding dessert to bring to her friend's barbecue. She mixes
chocolate and vanilla pudding in a large bowl for the adults. Then, she decides to make a smaller
portion for the kids. In a small bowl, Rosanne mixes half the amount of chocolate pudding and half
the amount of vanilla pudding. Which bowl of pudding is more chocolaty?
Answers
Answer:
None of the bowls
Step-by-step explanation:
It's because the amount of chocolate and vanilla in the pudding is the same,
which is why both are chocolatey; none are more chocolatey
Answer:
none
Step-by-step explanation:
i need help to solve this

Answers
Step-by-step explanation:
(6+r)^2 = 81 + r^2
36 + 12r+ r^2 = 81 + r^2
12r = 81-36 = 45
r = 15/4 = 3.75
State whether each of the following is an example of a positive correlation or a negative correlation.(a) Higher education level is associated with a larger annual income. (b) The smaller the class size, the more students believe they are receiving a quality education. (In other words, the larger the class size, the less likely students believe they are receiving a quality education.) (c) Increased testosterone is associated with increased aggression. (d) Rising prices of apples are associated with the sale of fewer apples
Answers
In (a), as education level increases, so does income, showing a positive correlation. In (b), as class size decreases, the belief that students are receiving a quality education increases, showing a negative correlation. In (c), as testosterone levels increase, so does aggression, indicating a positive correlation. In (d), as the price of apples rises, the sale of apples decreases, indicating a negative correlation
(a) is an example of a positive correlation, as higher education level and larger annual income are positively associated with each other.
(b) is an example of a negative correlation, as smaller class sizes are negatively associated with the belief that students are receiving a quality education.
(c) is an example of a positive correlation, as increased testosterone levels are positively associated with increased aggression.
(d) is an example of a negative correlation, as rising prices of apples are negatively associated with the sale of apples.
In a positive correlation, the two variables move in the same direction, so an increase in one variable is associated with an increase in the other variable. In a negative correlation, the two variables move in opposite directions, so an increase in one variable is associated with a decrease in the other variable.
Learn more about variables here: https://brainly.com/question/16906863
#SPJ11
What is the difference between a rectangular prism and a triangular prism?
The two bases of a rectangular prism are rectangles, while the two bases of a triangular prism are triangles.
A rectangular prism has two bases, while a triangular prism has one base,
A triangular prism has two bases, while a rectangular prism has one base.
A rectangular prism has two bases and three faces, while a triangular prism has two bases and four faces.
Dintro
Done
Answers
Answer:
The two bases of a rectangular prism are rectangles, while the two bases of a triangular prism are triangles.
Step-by-step explanation:
Any prism has two bases. Since we are talking about a rectangular prism and a triangular prism both must have two bases.
For example, a square prism has two bases and they are both square.
In this case a rectangular prism has two bases that are rectangles and a triangular prism also has two bases and both bases are triangles.
Note: For the figure to have only one base it must be called a pyramid.
Thus, the answer is:
The two bases of a rectangular prism are rectangles, while the two bases of a triangular prism are triangles
Answer:
a
Step-by-step explanation:
The annual snowfall in city a is 69.8 inches. this is 14.5 inches more than times the snowfall in city b. find the annual snowfall for city b.
Answers
The annual snowfall for City B is approximately 4.81 inches.
To find the annual snowfall for City B, we need to solve the equation given in the question: 69.8 = 14.5x, where x represents the snowfall in City B.
This simplifies to:
69.8 / 14.5 = x
This simplifies to:
4.81 ≈ x
average rainfall https://brainly.com/question/28576955
#SPJ11
please work this out

Answers
Answer:
? = 85°
Step-by-step explanation:
the sum of the interior angles of a polygon is
sum = 180° (n - 2) ← n is the number of sides
here n = 5 , then
sum = 180° × 3 = 540°
sum of the angles around a point = 360° , so
interior angle on right = 360° - 250° = 110°
sum the interior angles and equate to 540°
110° + 115° + 120° + 110° + ? = 540° , that is
455° + ? = 540° ( subtract 455° from both sides )
? = 85°
Suppose a house has a floor area of 2,250 square feet. What is this area in units ofsquare centimeters?A) 2.42 cm2 D) 6.86 × 104 cm2B) 2.09 × 106 cm2 E) 101 cm2C) 5.02 × 104 cm2
Answers
The area in units of square meter is 2,090,318.4 sq cm, under the given condition that a house has a floor area of 2,250 square feet. So , the correct option from the following is Option B.
To convert 2,250 square feet to square centimeters, we can use the conversion factor of 1 square foot = 929.0304 square centimeters⁵. Therefore,
2,250 sq ft = 2,250 x 929.0304 sq cm/ sq ft = 2,090,318.4 sq cm.
The area in units of square meter is 2,090,318.4 sq cm, under the given condition that a house has a floor area of 2,250 square feet. So , the correct option from the following is Option B.
To learn more about area ,
https://brainly.com/question/31299049
#SPJ4
IF YOU SOLVE THIS CORRECTLY WITH EXPLANATION U WILL GET BRAINILEST
-2r(8r+5)
Answers
Answer:
-16r^2 - 10r
Step-by-step explanation:
all you got to do is distribute
a house is 13 ft tall. its shadow is 20 ft long at the same time the shadow of a nearby building is 170 ft long. find the height of the building.
Answers
The height of the building after using proportion is 110.5 ft.
What is proportion ?
The main conceptual underpinnings on which proportion is described are ratio and fractions. When two ratios are written as a fraction using the formula a/b, ratio a:b, and then a proportion, they are equal. A and b in this situation can be any two integers. For grasping the myriad concepts in science and mathematics, the ratio and proportion are crucial constructing elements. With the right amount of proportion, a variety of problems in daily life, such as those encountered in the kitchen or in business when processing transactions, can be resolved. It facilitates comparison by establishing a relationship between two or more quantities.
Here House height = 13ft
Shadow of the house height = 20 ft
Shadow of the building height = 170ft
Noe using proportion ,
=> \(\frac{House height}{shadow of the house} = \frac{building height}{shadow of the building}\)
=> \(\frac{13}{20} = \frac{x}{170}\)
=> x=\(\frac{13*170}{20}\) =110.5 ft.
Hence the height of the building is 110.5 ft tall.
To learn more about proportion refer the below link
https://brainly.com/question/1496357
#SPJ4
Mrs. James has $40.50 to spend at the store. She wants to buy a dress that costs thirty dollars and necklaces that cost $3.50. How many necklaces can she buy?
Answers
Answer:
3 necklaces
Step-by-step explanation:
$40.50-$30.00=$10.50 Subtract her total money and cost of dress
$10.50-$3.50=$6.00 subtract each necklace price from remaining money
$6.00-$3.50=$3.50 keep subtracting price of necklace
$3.50-$3.50=$0 that was 3 necklaces
if two solids are similar with a scale factor of p : q, then corresponding areas have a ratio of and corresponding volumes have a ratio of
Answers
If two solids are similar with a scale factor of p:q, then corresponding areas have a ratio of (p/q)^2 and corresponding volumes have a ratio of (p/q)^3.
When two solids are similar, it means that they have the same shape but different sizes. The scale factor of p:q means that one solid is scaled by a factor of p while the other is scaled by a factor of q.
When it comes to the corresponding areas, the ratio will be (p/q)^2. This is because the area of a two-dimensional figure is proportional to the square of its dimensions. So, if the scale factor is p:q, then the corresponding areas will be proportional to (p/q)^2.
Similarly, when it comes to the corresponding volumes, the ratio will be (p/q)^3. This is because the volume of a three-dimensional figure is proportional to the cube of its dimensions. So, if the scale factor is p:q, then the corresponding volumes will be proportional to (p/q)^3.
It is important to note that the scale factor must be the same for both the corresponding areas and the corresponding volumes. This is because the dimensions of the two solids are scaled by the same factor.
In summary, if two solids are similar with a scale factor of p:q, then corresponding areas have a ratio of (p/q)^2 and corresponding volumes have a ratio of (p/q)^3.
To know more about scale factor visit :
https://brainly.com/question/26202345
#SPJ11
At what point do the curves F(t) = (t, 1 − t, 3 + t²) and ū(s) = (3 — s, s − 2, s²) intersect? Find their angle of intersection
Answers
The curves intersect at two points and their angle of intersection is approximately 125.1° and 62.7°.
To find the point of intersection between two curves, we need to solve the system of equations:
t = 3 - s
1 - t = s - 2
3 + t² = s²
Simplifying the second equation, we get:
t + s = 3
Substituting t = 3 - s in the third equation, we get:
s⁴ - 6s³ + 17s² - 24s + 10 = 0
This quartic equation can be solved using numerical methods or factored using the rational root theorem. However, the solutions are rather messy and not easy to obtain by hand. So we'll use a graphing calculator to find the approximate values of s:
s ≈ 2.399, 0.313
Substituting each value of s back into the first equation, we get the corresponding values of t:
When s ≈ 2.399, t ≈ 0.601
When s ≈ 0.313, t ≈ 2.687
So the two curves intersect at approximately two points: (0.601, 0.399, 4.360) and (2.687, -1.687, 0.534).
To find the angle of intersection, we can use the dot product formula:
cosθ = (F'(t) · ū'(s)) / (|F'(t)| |ū'(s)|)
where F'(t) and ū'(s) are the derivatives of the respective curves, and |F'(t)| and |ū'(s)| are their magnitudes.
Differentiating the first curve, we get:
F'(t) = (1, -1, 2t)
Differentiating the second curve, we get:
ū'(s) = (-1, 1, 2s)
So the dot product is:
F'(t) · ū'(s) = -1 - 1 + 4ts
The magnitudes of the derivatives are:
|F'(t)| = √(1 + 1 + 4t²)
|ū'(s)| = √(1 + 1 + 4s²)
Substituting the values of t and s for each point of intersection, we get:
At (0.601, 0.399, 4.360):
cosθ ≈ (-2.398) / (2.440 * 2.248) ≈ -0.527
θ ≈ 125.1°
At (2.687, -1.687, 0.534):
cosθ ≈ (8.542) / (6.144 * 2.784) ≈ 0.459
θ ≈ 62.7°
Therefore, the curves intersect at two points and their angle of intersection is approximately 125.1° and 62.7°.
Learn more about intersection here:
https://brainly.com/question/12089275
#SPJ11
8th question combination or permutations

Answers
The number of distinct words that can be formed from the letter in the word MULTIPLY is of:
20,160 distinct words.
What is the arrangements formula?The number of possible arrangements of n elements(order n elements) is given by the factorial of n, that is:
\(A_n = n!\)
For the world multiply, we have that it is composed by 8 letters, while the letter l appears two times, hence the number of distinct words that can be formed from the letter in the word MULTIPLY is obtained as follows:
8!/2! = 20,160 distinct words.
More can be learned about the arrangements formula at https://brainly.com/question/20255195
#SPJ1
Put the plants into ascending order based on
their height.
Plant
Fern
Rose
Sunflower
Height (m)
338 118 118
100
Answers
Answer:
sunflower , fern ,rose, and plant
Express the function F(x) = (x - 3)²
in the form fog. f(x) = g(x) =
Answers
To express the function F(x) = (x - 3)² in the form fog, we need to find two functions, f(x) and g(x), such that F(x) = (f ∘ g)(x).
Let's start by expanding F(x):
F(x) = (x - 3)²
= (x - 3)(x - 3)
= x² - 6x + 9
Now, let's express F(x) in terms of f(g(x)):
F(x) = (f ∘ g)(x)
Comparing the expanded form of F(x) with the expression for (f ∘ g)(x), we can deduce that:
f(x) = x²
g(x) = x - 3
So, we can express F(x) = (x - 3)² in the form fog as:
F(x) = (f ∘ g)(x) = f(g(x)) = (g(x))²
= (x - 3)²
Therefore, f(x) = x² and g(x) = x - 3 form the composition f ∘ g such that F(x) can be expressed as (f ∘ g)(x).
Learn more about functions here
https://brainly.com/question/11624077
#SPJ11
G is a trigonometric function of the form g(x)=a sin(bx+c)+d The function intersects its midline at (-1,6) and has a minimum point at (-3.5,3). Find the formula for g(x). Give an exact expression.
Answers
Answer:
g(x) = 3*sin((-15/4)*pi*x + (-15/4)*pi) + 6
Step-by-step explanation:
The function has the form:
g(x) = a*sin(b*x + c) + d
We know that:
The midline is at (-1, 6)
The midline is the value of g(x) when the sin(x) part is equal to zero
Then the midline is y = 6 = d
g(x) = a*sin(b*x + c) + 6
And from this we also know that:
sin(b*-1 + c) = 0,
We also know that the minimum is at (-3.5, 3)
The minimum is the y-value when the sin(x) part is equal to -1
Then
sin(b*-3.5 + c) = -1
And:
g(-3.5) = 3 = a*(-1) + 6
3 = -a + 6
a = -3 + 6 = 3
The equation is something like:
g(x) = 3*sin(b*x + c) + 6
To find the values of b and c, we need to use the two remaining equations:
sin(b*-3.5 + c) = -1
sin(b*-1 + c) = 0
We also know that:
Sin(0 ) = 0
sin( (3/2)*pi) = -1
where pi = 3.14
Then we can just write:
b*-1 + c = 0
b*-3.5 + c = (3/2)*pi
From the first one, we get:
-b + c = 0
c = b
Replacing that on the other equation we get:
c*-3.5 + c = (3/2)*pi
c*(-3.5 + 1) = (3/2)*pi
c*(-2.5) = (3/2)*pi
c = (3/2)*pi/(-2.5)
and:
-2.5 = -5/2
c = (3/2)*(-5/2)*pi = (-15/4)*pi
Then the equation becomes:
g(x) = 3*sin((-15/4)*pi*x + (-15/4)*pi) + 6
The trigonometric function equation becomes \(g(x)=3 sin(-1.88x-1.88)+6\)
The function has the form:
\(g(x)=a sin(bx+c)+d\)
The midline is at (-1, 6)
So, the midline is y = 6 = d
\(g(x)=a sin(bx+c)+6\)
We know that the midline is the value of g(x) when the sin(x) part is equal to zero
Given that The function intersects its midline at (-1,6) and has a minimum point at (-3.5,3).
\(sin(-1*b + c) = 0,\)
The minimum is the y-value when the sin(x) part is equal to -1
\(sin(-3.5*b + c) = -1\)
Since, \(g(-3.5) = 3 = a*(-1) + 6\)
\(a = -3 + 6 = 3\)
Now equation become,
\(g(x) = 3*sin(b*x + c) + 6\)
To find the values of b and c, we need to use the two remaining equations:
\(sin(-3.5b + c) = -1=sin( (3/2)* \pi)\\\\ -3.5b + c = (3/2)* \pi\)
\(sin(-1b + c) = 0=sin(0)\\\\-b+c=0\\\\b=c\)
Substituting b = c in above equation and \(\pi=3.14\)
We get,
\(-3.5c + c = (3/2)*\pi\\\\-2.5c=4.71\\\\c=-1.88\)
also \(b=-1.88\)
Therefore, equation becomes \(g(x)=3 sin(-1.88x-1.88)+6\)
Learn more:
https://brainly.com/question/13729598
what does parallelepiped focus on
Answers
Answer:
A parallelepiped has three sets of four parallel edges; the edges within each set are of equal length. Parallelepipeds result from linear transformations of a cube (for the non-degenerate cases: the bijective linear transformations).
Step-by-step explanation:
A parallelepiped focuses on three-dimensional figures formed by six parallelograms.
How to explain the parallelepiped?A parallelepiped shape has the following features
They are three-dimensional figuresThey are formed by 6 parallelogramsOpposite parallelograms are congruentThink of a cube or a cuboid.
Notice that they contain squares and rectangles
A parallelepiped is to a parallelogram as a square is to a cube and a rectangle to a cuboid
Read more about parallelepiped at:
https://brainly.com/question/3050890
#SPJ11
2. A sum of $400 was shared between Samantha and Jade. Samantha received S100 more than Jade. a) If Jade received $150, how much money did Samantha receive? (1 mark) Samanth received $ b) Determine the ratio used to share the money between Samantha and Jade. (2 marks) The ratio in its lowest terms =
Answers
Answer:
Samantha share =$250
ratio = 5:3
Step-by-step explanation:
Samantha
\( = jade + 100\)
jade
\(150\)
samantha
\(150 + 100 = 250\)
ratio
250:150
5:3
Find the area of hexagon DEFGHI.

Answers
Step-by-step explanation:
Break it up into two trapezoids as shown
area = trap1 + trap2
= 2 * (7+3) / 2 + 3 * ( 7 + 3) / 2 = 10 + 15 = 25 units^2

Which picture has a line of symmetry
Answers
Answer: there is so picture
Step-by-step explanation: it should give you the option when you ask the question it’s the little paper clip
The ratio of violins two cellos is 8 to 3. If there are 24 violins, how many cellos are there?
Answers
Answer:
9
Step-by-step explanation:
24/8=3
3x3=9
Answer:
9
Step-by-step explanation:
A population consists of the following five values: 11, 13, 15, 17, and 22. a. List all samples of size 3, and compute the mean of each sample. (Round your mean value to 2 decimal places.) 1 2 3 4 5 6 7 8 9 10 B. Compute the mean of the distribution of sample means and the population mean Sample means: Population Mean:
Answers
The population mean is 15.6 if A population consists of the following five values: 11, 13, 15, 17, and 22.
What is Mean ?
In statistics, the mean is a measure of central tendency of a set of numerical data. It is commonly referred to as the average, and is calculated by adding up all the values in the data set and dividing the sum by the total number of values.
a. To list all samples of size 3, we can take all possible combinations of 3 values from the population:
{11, 13, 15}: mean = 13
{11, 13, 17}: mean = 13.67
{11, 13, 22}: mean = 15.33
{11, 15, 17}: mean = 14.33
{11, 15, 22}: mean = 16
{11, 17, 22}: mean = 16.67
{13, 15, 17}: mean = 15
{13, 15, 22}: mean = 16.67
{13, 17, 22}: mean = 17.33
{15, 17, 22}: mean = 18
b. To compute the mean of the distribution of sample means, we need to find the mean of all the sample means computed in part (a). There are 10 sample means, so we add them up and divide by 10:
(13 + 13.67 + 15.33 + 14.33 + 16 + 16.67 + 15 + 16.67 + 17.33 + 18) ÷10 = 15.4
To compute the population mean, we simply take the average of the population values:
(11 + 13 + 15 + 17 + 22) ÷ 5 = 15.6
Therefore, the population mean is 15.6
To learn more about Mean from given link.
https://brainly.com/question/21533310
#SPJ1
Referring to the figure, find the measure of arc MLK

Answers
Measure of arc MLK is 270°
Explanation:Angle MKL = 135 degrees
We are looking for the measure of the arc MLK
The diagram shows an angle formed by a chord (MK) and tangent
The relationship between angle formed by a chord and tangent:
\(Inscribed\text{ angle = }\frac{1}{2}\text{ m of arc MLK}\)Measure of arc MLK:
\(\begin{gathered} \text{Measure of arc MLK = 2(inscribed angle)} \\ \\ In\text{scribed angle = 135}\degree\text{ } \\ \text{Measure of arc MLK = 2(135)} \\ \text{Measure of arc MLK = }270\degree \end{gathered}\)
And artist wants to frame a square painting the area of the painting is X to second power -10 X -39 in.² and the frame is 3 inches wide and all size ruined expression for the total area of the frame painting in terms of x
Answers
Answer:
2345679
Step-by-step explanation:
Find k.
10 mi
60⁰
K
30⁰
