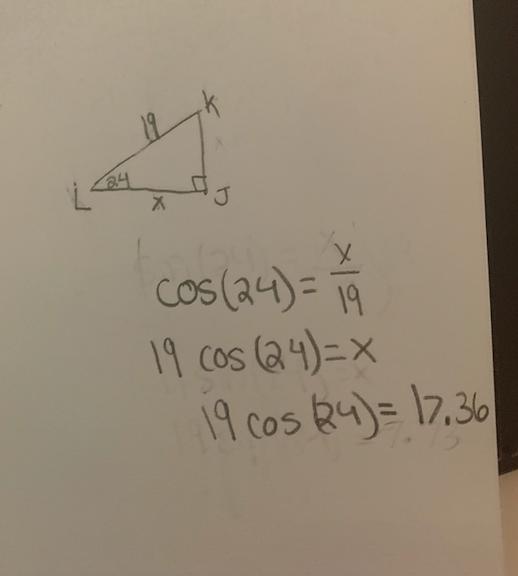Compare the table and equation. x y 1 3 2 6 3 9 Equation: y = 4x Which representation has the greatest slope?

a) The equation has the greatest slope.
b) The table has the greatest slope.
c) The table and equation have the same slope.
d) Their slopes cannot be determined.

HELLO

I NEEDED HELP WITH THE SAME QUESTION SO I PUT IT UP WITH A PIC SO U CAN ALSO GET AN ANSWER FROM THERE

HERE YA GO <3

https://brainly.com/question/24188218?referrer=searchResults

Answer:

heyy i did this problem a while ago and got kinda stuck on it

The expression that describe the end behavior of the expression f(x)= (3.25)^x + 6 is The curve begins infinitely close to the line y equals 6 in the second quadrant.

The behavior of the graph of a function at its "ends" on the x-axis is referred to as the end behavior of a function, f.

For example, if we look at the right end of the x-axis (as x approaches + ∞) and the left end of the x-axis (as x approaches - ∞), the end behavior of a function explains the trend of the graph.

The graph of the function is attached and from the graph it shows that the graph continued to tend towards towards line y = 6

Learn more about end behavior here:

https://brainly.com/question/28954897

#SPJ1

Answer:

that is your answer 10.34

Step-by-step explanation:

Notice: The literal factors are all the combinations of a and b where the sum of the exponents is 4: a4, a³b, a²b², ab³, b4 ... The solution to the problem of the binomial coefficients without actually ... The upper index n is the exponent of the expansion; the lower index k indicates which term ... 1a5 + a4b + a3b² + a²b3 + ab4 + b5.

Answer:

If you've more doubts you can ask :)

Step-by-step explanation:

If the centre of a circle is (a, b) and radius r, then the equation of the circle is :

\((x - x)^2 + (y-b)^2 = r^2\)

First we will find the centre, (a , b):

\(a = \frac{3+(-1)}{2} = \frac{2}{2} = 1\\\\b = \frac{-2 + 4}{2} = \frac{2}{2} = 1\)

Find radius:

\(Radius, r = \frac{Diameter}{2}\)

Diameter is the distance between (-1, 4) and (3, -2)

\(diameter = \sqrt{(x_2 - x_1)^2 +(y_2-y_1)^2} \\\\\)

             \(= \sqrt{(3-(-1)^2 + (-2-4)^2} \\\\=\sqrt{16 + 36}\\\\=\sqrt{52}\\\\=\sqrt{4 \times 13}\\\\=2\sqrt{13} \ units\)

Therefore , \(r = \frac{2 \times \sqrt{13} }{2} = \sqrt{13} \ units\)

Equation of the circle is :  

                                 \((x - 1)^2 +(y-1)^2 = 13\)

Answer:

18 ft or 37.6 ft

Step-by-step explanation:

A + B = 34

A + C = 16

34^2 + 16^2 =BC^2

1156 + 256 = BC^2

1412 = BC^2

37.57=BC

Answer:

there  you go

Step-by-step explanation:

have a good day/night

Answer:

1.39285714286

Step-by-step explanation:

\(1\frac{1}{3} + 2\frac{1}{4} = \frac{3*1+1}{3} + \frac{4*2+1}{4} = \frac{4}{3} + \frac{9}{4} = \frac{4*4}{3*4} + \frac{9*3}{4*3} = \frac{16}{12} + \frac{27}{12} = \frac{16+27}{12}=\frac{23}{12} = 1\frac{11}{12}\)

Step-by-step explanation:

blue=60%

yellow= 30%

red=10%

hope it helps

please mark me brainliest

The difference between the observed and expected number of late departures is statistically significant, we need to perform a binomial test by calculating the probability of observing 16 or more late departures out of 300 flights assuming the null hypothesis is true. If the resulting p-value is less than 0.05, we can conclude that the difference is statistically significant.

Based on the given information, an airline with a 95% on-time departure rate has 16 out of 300 flights with late departures. The question asks whether the difference between what occurred (16 late departures) and what you would expect by chance is statistically significant.
To determine if the difference is statistically significant, we need to conduct a hypothesis test. In this case, we can use a binomial test since we are dealing with two possible outcomes: on-time departure or late departure.
The null hypothesis (H0) assumes that the observed number of late departures is equal to what would be expected by chance. The alternative hypothesis (Ha) assumes that there is a significant difference between the observed and expected values.
In this case, the expected number of late departures can be calculated by multiplying the total number of flights (300) by the expected on-time departure rate (95%). This gives us an expected value of 300 * 0.05 = 15.
To perform the binomial test, we can calculate the probability of observing 16 or more late departures out of 300 flights, assuming the null hypothesis is true. This probability can be calculated using the binomial probability formula or by using statistical software.
If the resulting probability (also known as the p-value) is less than the significance level (usually 0.05), we can reject the null hypothesis and conclude that the difference between what occurred and what would be expected by chance is statistically significant. Otherwise, if the p-value is greater than 0.05, we fail to reject the null hypothesis and conclude that the difference is not statistically significant.
For more such questions on probability

https://brainly.com/question/30390037

#SPJ8

Answer:

turn it 90 degrees, hope this helps

Step-by-step explanation:

Answer:

so go to the 120 degree line and make sure the line is straight across from zero and thin dray a line going from 120 down to the bottom of where the zero is  

Step-by-step explanation:

The period of the sound wave created by the tuba is approximately 0.0134 seconds.

The speed of sound in air is given as 343 meters per second. The formula relating the speed of sound, wavelength, and period of a wave is:

v = λ × f

Where:

v = speed of sound (343 m/s)

λ = wavelength (4.61 m)

f = frequency (unknown)

To find the period, we need to determine the frequency of the sound wave. The period (T) is the reciprocal of the frequency (f), so we can rewrite the formula as:

v = λ / T

Rearranging the equation to solve for the period (T), we get:

T = λ / v

Substituting the given values, we have:

T = 4.61 m / 343 m/s

Calculating the value, we find:

T ≈ 0.0134 seconds

Therefore, the period of the sound wave created by the tuba is approximately 0.0134 seconds.

for such more question on wavelength

https://brainly.com/question/10728818

#SPJ8

Answer:

60

Step-by-step explanation:

20 calls / 60 minutes

x calls / 180 minutes

60 x 3 = 180 minutes

20 x 3 = 60 calls

Answer:

Ms hodge will expect to receive 60 phone calls in 180 minutes.

Step-by-step explanation:

180 divided by 60 is 3

3x20= 60

Ms hodge will expect to receive 60 phone calls in 180 minutes.

there are 160 plastic cubes that can fit into the box.

Step-by-step explanation:

brainlist plz

Answer:

27

Step-by-step explanation:

I took the same test

Answer:

A regular prism with 10 faces and 12 vertices has 6 sides. This is because the number of faces and vertices are related by the equation F+2 = E+2V, where F is the number of faces, E is the number of edges, and V is the number of vertices. In this case, 10+2 = 12+2V, so V = 6 and the number of sides of the prism is also 6

Step-by-step explanation:

1. A regular prism has 10 faces and 12 vertices.

2. The number of faces and vertices is related by the equation F+2 = E+2V.

3. Where F is the number of faces, E is the number of edges, and V is the number of vertices.

4. In this case, 10+2 = 12+2V, so V = 6.

5. Therefore, the number of sides of the prism is also 6.

Answer:

  76 units

Step-by-step explanation:

You want the length of AC in the given triangular pyramid.

The Pythagorean theorem can be used to find the lengths of AD and CD.

  AD² + 40² = 41²

  AD² = 41² -40² = 81 . . . . . = 9²

and

  CD² +40² = 85²

  CD² = 85² -40² = 5625 . . . . . = 75²

It can also be used to find AC:

  AD² + CD² = AC²

  81 + 5625 = AC²

  AC = √5706 = 3√634 ≈ 76

The length of side AC is about 76 units.

__

Additional comment

The Pythagorean theorem tells you the square of the hypotenuse is the sum of the squares of the legs of a right triangle.

<95141404393>

Answer: The quotient is 3y² + 2y - 1.

Step-by-step explanation:

You can use long division to solve this expression by setting the dividend under the roof and the divisor outside as you would normally do when dividing numbers.

1) Look at the first term of the dividend, 15y³, and the first term of the divisor, 5y. Determine what value multiplied by 5y would give you 15y³. The answer is 3y², and given the number, you multiply it by the WHOLE divisor.

3y²(5y + 6) = 15y³ + 18y² <-- subtract this from the dividend.

2) Continue this process and make sure to drag down the next term for each new value you form after subtracting. Keep in mind of any negative values! When you reach up to -5y, determine what value multiplied by 5y would give you the value of -5y, which would be -1.

3) You should be left with a remainder of 0, leaving you with a quotient of 3y² + 2y - 1.

Answer:

0.0903

Step-by-step explanation:

Given that :

The mean = 1450

The standard deviation = 220

sample mean = 1560

\(P(X > 1560) = P( Z > \dfrac{x - \mu}{\sigma})\)

\(P(X > 1560) = P(Z > \dfrac{1560 - 1450}{220})\)

\(P(X > 1560) = P(Z > \dfrac{110}{220})\)

P(X> 1560) = P(Z > 0.5)

P(X> 1560) = 1 - P(Z < 0.5)

From the z tables;

P(X> 1560) = 1 - 0.6915

P(X> 1560) = 0.3085

Let consider the given number of weeks = 52

Mean \(\mu_x\) = np = 52 × 0.3085 = 16.042

The standard deviation =  \(\sqrt {n \time p (1-p)}\)

The standard deviation = \(\sqrt {52 \times 0.3085 (1-0.3085)}\)

The standard deviation = 3.3306

Let Y be a random variable that proceeds in a binomial distribution, which denotes the number of weeks in a year that exceeds $1560.

Then;

Pr ( Y > 20) = P( z > 20)

\(Pr ( Y > 20) = P(Z > \dfrac{20.5 - 16.042}{3.3306})\)

\(Pr ( Y > 20) = P(Z >1 .338)\)

From z tables

P(Y > 20) \(\simeq\) 0.0903

Answer:

I think its either 5 or 4 one of the 2

Use slopes and y-intercepts to determine if the lines 5x + 2y = -3 and 2x - y = -2 are parallel.

step 1

we have the line

5x + 2y = -3

isolate the variable y

2y=-5x-3

y=-2.5x-1.5

the slope is m=-2.5

y-intercept b=-1.5

step 2

we have

2x - y = -2

y=2x+2

the slope is m=2

the y-intercept is b=2

step 3

Compare their slopes

m=-2.5

m=2

the slopes are not equal

that means

the lines are not parallel

Answer: Total old car is $2955.89, new car $1080.94 *for 3yrs

Step-by-step explanation:

Old= [(100/19)($2.36)(52)+$770]*3 = $2955.89

New=[(100/34)($2.36)(52)+20(12)]*3= $1080.94

I keep the old car # 1

Given statement solution is :- The present value of R13,000 per year invested for 8 years at 10% compound interest is approximately R69,776.60.

To calculate the present value of an investment with compound interest, we can use the formula for the present value of an annuity:

PV = A *\((1 - (1 + r)^(-n)) / r\)

Where:

PV = Present value

A = Annual payment or cash flow

r = Interest rate per period

n = Number of periods

In this case, the annual payment (A) is R13,000, the interest rate (r) is 10% per year, and the investment is made for 8 years (n).

Using the formula and substituting the given values, we can calculate the present value:

PV = \(13000 * (1 - (1 + 0.10)^(-8)) / 0.10\)

Calculating this expression:

PV = \(13000 * (1 - 1.10^(-8)) / 0.10\)

= 13000 * (1 - 0.46318) / 0.10

= 13000 * 0.53682 / 0.10

= 6977.66 / 0.10

= 69776.6

Therefore, the present value of R13,000 per year invested for 8 years at 10% compound interest is approximately R69,776.60.

For such more questions on present value

https://brainly.com/question/30390056

#SPJ8

The complete square form of - 3x² + 33 = 48x is [x + 8]² = 75

To do this, we add and subtract a constant term to the quadratic expression to make it a perfect square.

In this case, we use the formula x² + 2bx + b² = (x + b)² to rewrite the quadratic expression as a perfect square trinomial, and then we solved for the variable by isolating the squared term and taking the square root.

Here we have

- 3x² + 33 = 48x

Keep 'x' terms on one side and constant terms sides on another side

=> - 3x² - 48x = - 33

Divide by - 3 on both sides

=> -3(x² + 4x)/3 = - 33/3  

=> x² + 16x = 11      

Take half of the 'x' term and square it and add on both sides

=> x² + 2(8x) (x) + (8)² = 11 + (8)²  

Which is in the form of x² + 2bx + b² = (x + b)²

=> [x + 8]² = 75

Therefore,

The complete square form of - 3x² + 33 = 48x is [x + 8]² = 75

Learn more about Completing the square at

https://brainly.com/question/14270950

#SPJ1

Ab=3.14xRadious to the power of 2

then to the area of the rectange you do B x H = YOUR ANSWER

Using the combination formula, it is found that:

\(C_{n,x}\) is the number of different combinations of x objects from a set of n elements, given by the following formula, involving factorials. It is used when the order in which the elements are chosen does not matter.

\(C_{n,x} = \frac{n!}{x!(n-x)!}\)

In the context of this problem, we have that seven tablets are chosen from a set of 28 tablets, hence the number of selections that can be made is given by:

\(C_{28,7} = \frac{28!}{7!21!} = 1,184,040\)

For two defective tablets, the selections are given as follows:

Hence the number of selections is calculated as follows:

\(C_{23,5}C_{5,2} = \frac{23!}{5!18!} \times \frac{5!}{2!3!} = 336,490\)

A similar problem, also about the combination formula, is given at https://brainly.com/question/25821700

#SPJ1

Answer:

$3.66.

Step-by-step explanation:

1 yard is equal to 3 feet. So, a 2-yard piece of brass wire is equivalent to 6 feet of brass wire. To find the price per foot, we need to divide the total cost by the total length. So, the price per foot is

To prove that line segment a is parallel to line segment d, based on the given information, we can utilize the properties of perpendicular and parallel lines.

Given that a is perpendicular to b and b is perpendicular to c, we know that angles formed between a and b, as well as between b and c, are right angles. Let's denote these angles as ∠1 and ∠2, respectively.

Now, since c is parallel to d, we can conclude that the corresponding angles ∠2 and ∠3, formed between c and d, are congruent.Considering the fact that ∠2 is a right angle, it can be inferred that ∠3 is also a right angle.

By transitivity, if ∠1 is a right angle and ∠3 is a right angle, then ∠1 and ∠3 are congruent.Since corresponding angles are congruent, and ∠1 and ∠3 are congruent, we can deduce that line segment a is parallel to line segment d.

Thus, we have successfully proven that a is parallel to d based on the given information and the properties of perpendicular and parallel lines.

For more such questions on line segment

https://brainly.com/question/30756145

#SPJ8

Answer:

17.36

Step-by-step explanation:

since there was not a diagram, this is only how i assume the problem would be set up. see the attachment for how i solved it