Answers
SOLUTION
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: Write the given expressions.
\(\text{2}.7\times10^3\Rightarrow27\times10^3\)STEP 2: Divide them into two different expressions
\(\begin{gathered} \text{2}.7\times10^3=\text{?} \\ 27\times10^3=\text{?} \end{gathered}\)STEP 3: Solve the first expression.
\(\begin{gathered} \text{2}.7\times10^3 \\ 10^3=1000 \\ =1000\times\: 2.7 \\ \mathrm{Multiply\: the\: numbers\colon}\: 2.7\times\: 1000=2700 \\ =2700 \end{gathered}\)STEP 4: Solve the second expression
\(\begin{gathered} 27\times10^3 \\ 10^3=1000 \\ =27\times\: 1000 \\ \mathrm{Multiply\: the\: numbers\colon}\: 27\times\: 1000=27000 \\ =27000 \end{gathered}\)STEP 5: Compare the two simplified answers
\(\begin{gathered} 2700\Rightarrow27000 \\ It\text{ can be se}en\text{ that the output on the left is less than the output on the right} \\ i.e,\text{ }2700<27000 \\ \text{2}.7\times10^3<27\times10^3 \end{gathered}\)Hence, the comparison of the expressions gives:
\(\text{2}.7\times10^3<27\times10^3\)Less than(<)
Related Questions
can you help please this is really important

Answers
The value of x is 10 and the length of SU is 50.
Here SU is the line and T is the mid-point of the line
So from this we have
SU = ST + TU
ST = TU
SU = 2ST = 2TU
ST = 3x - 5 and TU = 2x + 5
As ST = TU
3x - 5 = 2x + 5
x = 10
SU = 2ST
= 2( 3x - 5)
= 2( 3 × 10 - 5)
= 2( 30 - 5)
= 2× 25
= 50
Therefore the value of x is 10 and the length of SU is 50.
To know more about the line and the mid-point refer to the link given below:
https://brainly.com/question/896396
#SPJ9
A woman wants to measure the height of a nearby tower. She places a 10 ft pole in the shadow of the tower so that the shadow of the pole is exactly covered by the shadow of the tower. The total length of the tower's shadow is 190 ft, and the pole casts a shadow that is 3.25 ft long. How tall is the tower? Round your answer to the nearest foot. (The figure is not drawn to scale.)

Answers
Step-by-step explanation:
Let's denote the height of the tower as "h" feet.
According to the given information, the length of the pole's shadow is 3.25 ft, and the total length of the tower's shadow (including the shadow of the pole) is 190 ft.
We can set up a proportion using the similar triangles formed by the tower, its shadow, the pole, and its shadow:
height of the tower / length of the tower's shadow = height of the pole / length of the pole's shadow
h / 190 = 10 / 3.25
Cross-multiplying:
h * 3.25 = 10 * 190
h * 3.25 = 1900
Dividing both sides by 3.25:
h = 1900 / 3.25
h ≈ 584.62
Rounding to the nearest foot, the height of the tower is approximately 585 feet.
calculate the mean deviation of the following numbers 8,5,7,10,3,4,31,12.
Answers
Answer:
5.75.
Step-by-step explanation:
The mean = (8+5+7+10+3+4+31+12)/ 8
= 80/8
= 10.
Now we calculate the difference of each value from the mean We take the absolute ( positive) differences
10 - 8 = 2
10 - 5 = 5
10 - 7 = 3
10 - 10 = 0
10-3 = 7
10 = 4 = 6
10 - 31 = 21
10 - 12 = 2
Sum of the differences = 46
and the mean deviation is 46/8 = 5.75.
hey any help? (please make sure this is correct i'd appreciate it)

Answers
Answer:
Below
Step-by-step explanation:
Line AB is of the form y = mx + b where m is the slope = 2
Line BC is perpendicular to this and will have slope - 1/m = - 1/2 and includes the point C (0,6)
The point slope form of line BC will then be
( y-6) = - 1/2 ( x - 0) which can be re-arranged to
y = - 1/2x + 6 < ==== equation for line BC
select the correct answer which table corresponds to the graph above

Answers
Answer:
(b)
Step-by-step explanation:
graph plotting
when x = -3 , y = 4
when x= -2 , y = 0
when x = -1 , y = -2
when x = 0 , y = -3
when x = 1, y = -3.5
The Coopers own two vehicles, a mini-van and sedan. The following functions represent the resale value of both cars, in thousands of dollars,
after x years.
Mini-Van: f(1) = 32(0.8)*
Sedan: g(t) = 25(0.8)
Write function t that represents the total resale value, in thousands of dollars, of the two vehicles.
Answers
Answer:
\(h(x) = 57(0.8)^x\)
Step-by-step explanation:
Given
\(f(x) = 32(0.8)^x\)
\(g(x) = 25(0.8)^x\)
Required
A function that represents the total resale value of the two vehicles
To do this, we simply add up the functions
\(h(x) = f(x) + g(x)\)
\(h(x) = 32(0.8)^x + 25(0.8)^x\)
Factorize
\(h(x) = (32 + 25)(0.8)^x\)
\(h(x) = 57(0.8)^x\)
A positive integer is 4 less than another. If 3 times the reciprocal of the smaller integer is subtracted from the reciprocal of the larger integer, then the result is −67. Find all pairs of integers that satisfy this condition.
Answers
Answer:
(0.0147, 4.0147) and (-4.04, 0.04)
Step-by-step explanation:
Let the smaller number be x
Let the larger number be y
If a positive integer is 4 less than another, then;
x = y - 4 ...1
If 3 times the reciprocal of the smaller integer is subtracted from the reciprocal of the larger integer and result is -67, then;
1/y - 3(1/x) = -67
1/y -3/x = -67 ...2
Substitute 1 into 2
1/y - 3/y-4 = -67
y-4-3y/y(y-4) = -67
-4-2y = -67(y^2-4y)
- 4-2y = -67y^2 +268y
-67y^2 +268y+2y + 4 = 0
-67y^2 +270y + 4 =0
67y^2 -270y - 4 = 0
Factorize
-270±√270² - 4(-4)(67)/2(67)
= -270±√72,900+1072/134
= -270±271.97/134
= -270 -271.97/134 and -270 +271.97/134
= -541.97/134 and 1.97/134
x = 0.0147 and -4.04
y = x+4
y = 0.0147+4
y = 4.0147
If x = -4.04
y = -4.04 + 4
y = 0.04
Hence the pair of values are (0.0147, 4.0147) and (-4.04, 0.04)
Question in the pic, please explain your answer

Answers
The statement translated to an algebra equation will give the value of the unknown number w = 11/5
What is algebra?Algebra is the branch of mathematics that helps to represent problems or values in the form of mathematical expressions using letters to represent unknown values.
Let us represent the unknown number with the letter w so that the statement can be written as the equation:
5w - 8 = 3
add 8 to both sides
5w - 8 + 8 = 3 + 8
5w = 11
divide through by 5
5w/5 = 11/5
w = 11/5
Therefore, the statement translated to an algebra equation will give the value of the unknown number w = 11/5
Read more about algebra here: https://brainly.com/question/4344214
#SPJ1
Solve by Factoring:
2x^2 - x - 3 = 0
Answers
Answer:
x = 3/2 or x = -1
Step-by-step explanation:
2x² - x - 3 = 0
2*(-3) = -6
Factors of -6:
(-1, 6), (1, -6), (-2, 3), (2, -3)
We need to find a pair that adds up to the co-eff of x which is (-1)
Factors :(2,-3)
2 - 3 = -1
so, 2x² - x - 3 = 0 can be written as:
2x² + 2x - 3x - 3 = 0
⇒ 2x(x + 1) -3(x + 1) = 0
⇒ (2x - 3)(x + 1) = 0
⇒ 2x - 3 = 0 or
x + 1 = 0
⇒ 2x = 3 or x = -1
⇒ x = 3/2 or x = -1
Find the value of x in the figure.

Answers
6x-10=5x+12
X=22
Match the following reasons with the statements to complete the following proof.
Given: AD is a straight line and m
CBD = m /DBE
To Prove: m ABC+mDBE=180°.
B
1. m
CBD=mDBE
2. ZABC, CBD are supplementary
3. mABC+m CBD = 180°
4. m ABC+mDBE = 180°
DY
3
1
2
Substitution
Given
Definition of supplementary
exterior sides in opposite rays
Answers
1. Given: AD is a straight line and m CBD = m DBE (Given statement) 2. Since AD is a straight line, Z ABC and Z CBD are supplementary angles (Definition of supplementary angles) 3. We can write the equation: m ABC + m CBD = 180° (Definition of supplementary angles) 4. Substitute m CBD with m DBE (Substitution) 5. We have m ABC + m DBE = 180° (Substitution)
1. Given: AD is a straight line and m CBD = m DBE (Given statement)
2. Since AD is a straight line, it forms a straight angle with any other angle on it.
3. By the definition of a straight angle, we know that a straight angle measures 180°.
4. From the given statement, we can deduce that m CBD = m DBE.
5. When two angles are equal, their measures can be substituted for each other in any equation or statement.
6. Now, consider triangle ABC and triangle DBE. The sum of the angles in a triangle is always 180°.
7. In triangle ABC, we have m ABC + m BAC + m BCA = 180°.
8. In triangle DBE, we have m DBE + m BED + m EDB = 180°.
9. Since m BAC and m BED are both part of the straight angle formed by AD, they are supplementary angles and sum up to 180°.
10. Therefore, we can rewrite the equations as m ABC + m BCA + m BAC = 180° and m DBE + m EDB + m BED = 180°.
11. By substituting m CBD with m DBE (from the given statement), we have m ABC + m BCA + m BAC = 180° and m ABC + m BCA + m BED = 180°.
12. Subtracting the common terms from both equations, we get m BAC = m BED.
13. Using the transitive property, we can deduce that m ABC + m BCA = m EDB.
14. Combining the equations, we have m ABC + m DBE = m EDB.
15. Since m EDB and m ABC are supplementary angles (as they both share the straight angle formed by AD), their sum is 180°.
16. Therefore, we can conclude that m ABC + m DBE = 180°.
For more such questions on supplementary angles, click on:
https://brainly.com/question/12919120
#SPJ8
Find the missing side length.
Assume that all intersecting sides meet at right angles.
Be sure to include the correct unit in your answer.
5 yd
10 yd
14 yd
?
4 yd
11 yd

Answers
Answer:
6 yards
Step-by-step explanation:
yeah-ya........ right?
1) Convert 2-7i to trigonometric form
2) Use the n-th roots theorem to find the requested roots of the given complex number.
Find the cube roots of 125
Answers
Answer:
1) \(\sqrt{53}(\cos286^\circ+i\sin286^\circ)\)
2) \(\displaystyle 5,-\frac{5}{2}+\frac{5\sqrt{3}}{2}i,-\frac{5}{2}-\frac{5\sqrt{3}}{2}i\)
Step-by-step explanation:
Problem 1
\(z=2-7i\\\\r=\sqrt{a^2+b^2}=\sqrt{2^2+(-7)^2}=\sqrt{4+49}=\sqrt{53}\\\\\theta=\tan^{-1}(\frac{y}{x})=\tan^{-1}(\frac{-7}{2})\approx-74^\circ=360^\circ-74^\circ=286^\circ\\\\z=r\,(\cos\theta+i\sin\theta)=\sqrt{53}(\cos286^\circ+i\sin 286^\circ)\)
Problem 2
\(\displaystyle z^\frac{1}{n}=r^\frac{1}{n}\biggr[\text{cis}\biggr(\frac{\theta+2k\pi}{n}\biggr)\biggr]\,\,\,\,\,\,\,k=0,1,2,3,\,...\,,n-1\\\\z^\frac{1}{3}=125^\frac{1}{3}\biggr[\text{cis}\biggr(\frac{0+2(2)\pi}{3}\biggr)\biggr]=5\,\text{cis}\biggr(\frac{4\pi}{3}\biggr)=5\biggr(-\frac{1}{2}-\frac{\sqrt{3}}{2}i\biggr)=-\frac{5}{2}-\frac{5\sqrt{3}}{2}i\)
\(\displaystyle z^\frac{1}{3}=125^\frac{1}{3}\biggr[\text{cis}\biggr(\frac{0+2(1)\pi}{3}\biggr)\biggr]=5\,\text{cis}\biggr(\frac{2\pi}{3}\biggr)=5\biggr(-\frac{1}{2}+\frac{\sqrt{3}}{2}i\biggr)=-\frac{5}{2}+\frac{5\sqrt{3}}{2}i\)
\(\displaystyle z^\frac{1}{3}=125^\frac{1}{3}\biggr[\text{cis}\biggr(\frac{0+2(0)\pi}{3}\biggr)\biggr]=5\,\text{cis}(0)=5(1+0i)=5\)
Note that \(\text{cis}\,\theta=\cos\theta+i\sin\theta\) and \(125=125(\cos0^\circ+i\sin0^\circ)\)
Suppose we have a random sample of size n = 5 from a continuous uniform distribution on the interval [0, 1]. Find the probability that the third largest observation in the
sample is less than 0.7.
Answers
The probability that the third largest observation in the sample is less than 0.7 is 0.2401 = 24.01%.
How do we calculate?The sample size n = 5,
Therefore the order statistics will be represented as X₁, X₂, X₃, X₄, and X₅.
Probability that X₃ is less than 0.7:
Since X₃ is the third largest observation = (X₁ and X₂) < 0.7.
The probability that X₃ is less than 0.7 is (0.7)² = 0.49.
The Probability that X₁ and X₂ < or equal to 0.7 is found as:.
The probability that both X₁ and X₂ are less than or equal to 0.7 is (0.7)² = 0.49 because in a continuous uniform distribution, the probability of any single observation being less than 0.7 is 0.7 - 0 = 0.7.
We then get the product of both cases:
Probability = 0.49 * 0.49 = 0.2401
Learn more about Probability at:
https://brainly.com/question/24756209
#SPJ1
Use the discriminant to determine how many and what kind of solutions the quadratic equation 2x² - 4x = -2 has.
O two real solutions
Ono real or complex solutions
O two complex (nonreal) solutions
one real solution
Answers
The discriminant of the given quadratic equation is zero, which means that it has two real solutions.
What is a quadratic equation?
The polynomial equations of degree two in one variable of type
f(x) = ax² + bx + c = 0 and with a, b, c, ∈ R and a ≠ 0 are known as quadratic equations. It is a quadratic equation in its general form, where "a" stands for the leading coefficient and "c" is for the absolute term of f(x).
The discriminant's value reveals how many roots f(x) has:
- The quadratic function has two unique real roots if b² - 4ac > 0, otherwise it does not.
The quadratic function has one repeating real root if b² - 4ac = 0.
- The quadratic function has no true roots if b² - 4ac < 0.
The given quadratic equation is:
2x² - 4x = -2
2x² - 4x + 2 = 0
The general equation is :
ax² + bx + c = o
where discriminant is found using the formula b² - 4ac
Comparing the equations, we can write
a = 2
b = -4
c = 2
b² - 4ac = (-4)² - 4*2*2 = 16 - 16 = 0
Since the discriminant is equal to zero, it suggests that the quadratic equation has two equal real and rational roots.
Therefore the discriminant of the given quadratic equation is zero, which means that it has two real solutions.
To learn more about the quadratic equation, follow the link.
https://brainly.com/question/1214333
#SPJ1
its
A bag contains 5 green candies and 7 blue candies.
A piece of candy is selected at random, put back into the bag, and then
another piece of candy is chosen.
What is the probability that both pieces are green?
Answers
Answer:
\(P(Green\ and\ Green) = \frac{25}{144}\)
Step-by-step explanation:
Given
\(Green=5\)
\(Blue = 7\)
Required
\(P(Green\ and\ Green)\)
This is calculated as:
\(P(Green\ and\ Green) = P(Green) * P(Green)\)
Since, it is a probability with replacement, we have:
\(P(Green\ and\ Green) = \frac{Green}{Total} * \frac{Green}{Total}\)
So, we have:
\(P(Green\ and\ Green) = \frac{5}{12} * \frac{5}{12}\)
\(P(Green\ and\ Green) = \frac{25}{144}\)
Write and solve an inequality that represents the values of x for which the area of the rectangle will be at least 35 square feet.
Answers
Explanation:
There really is not enough information here. You have not indicated how x is related to the rectangle.Perhaps (as an alternative to the assumption I made [above]), you meant for x > 0 to be the length of one side of a square.
I have attached the answer in the picture.

Write an explicit formula for an, the nth term of the sequence 30, 35, 40
Answers
Answer:
The sequence is increasing by 5 at each step. So, we can write:
a1 = 30
a2 = 30 + 5 = 35
a3 = 30 + 25 = 40
a4 = 30 + 35 = 45
a5 = 30 + 4*5 = 50
We notice that the nth term is given by:
an = 30 + (n-1)5
So, the explicit formula for the nth term is:
an = 25n + 5
\(inverse function of \frac{3^x+2}{3^x-5}\)
Answers
Answer:
\((3 {}^{x} + 2)(3 {}^{x} + 2)\)
hope it is helpful to you
Element X is a radioactive isotope such that every 12 years, its mass decreases by half.
Given that the initial mass of a sample of Element X is 900 grams, how much of the
element would remain after 6 years, to the nearest whole number?
Answers
Answer:636
Step-by-step explanation: I just kno
Petrolyn motor oil is a combination of natural oil and synthetic oil. It contains 3 liters of natural oil for every 4 liters of synthetic oil. In order to make 497
liters of Petrolyn oil, how many liters of natural oil are needed?
Answers
Answer:
(3 / 7) * 497 = 213 liters of natural oil
************************************************************
As a double check:
(4 / 7) * 497 = 284 liters of synthetic oil needed
213 + 284 = 491 liters
Step-by-step explanation:
Does anybody know this? I am a bit confused and please answer it right cause if you don't know it don't bother
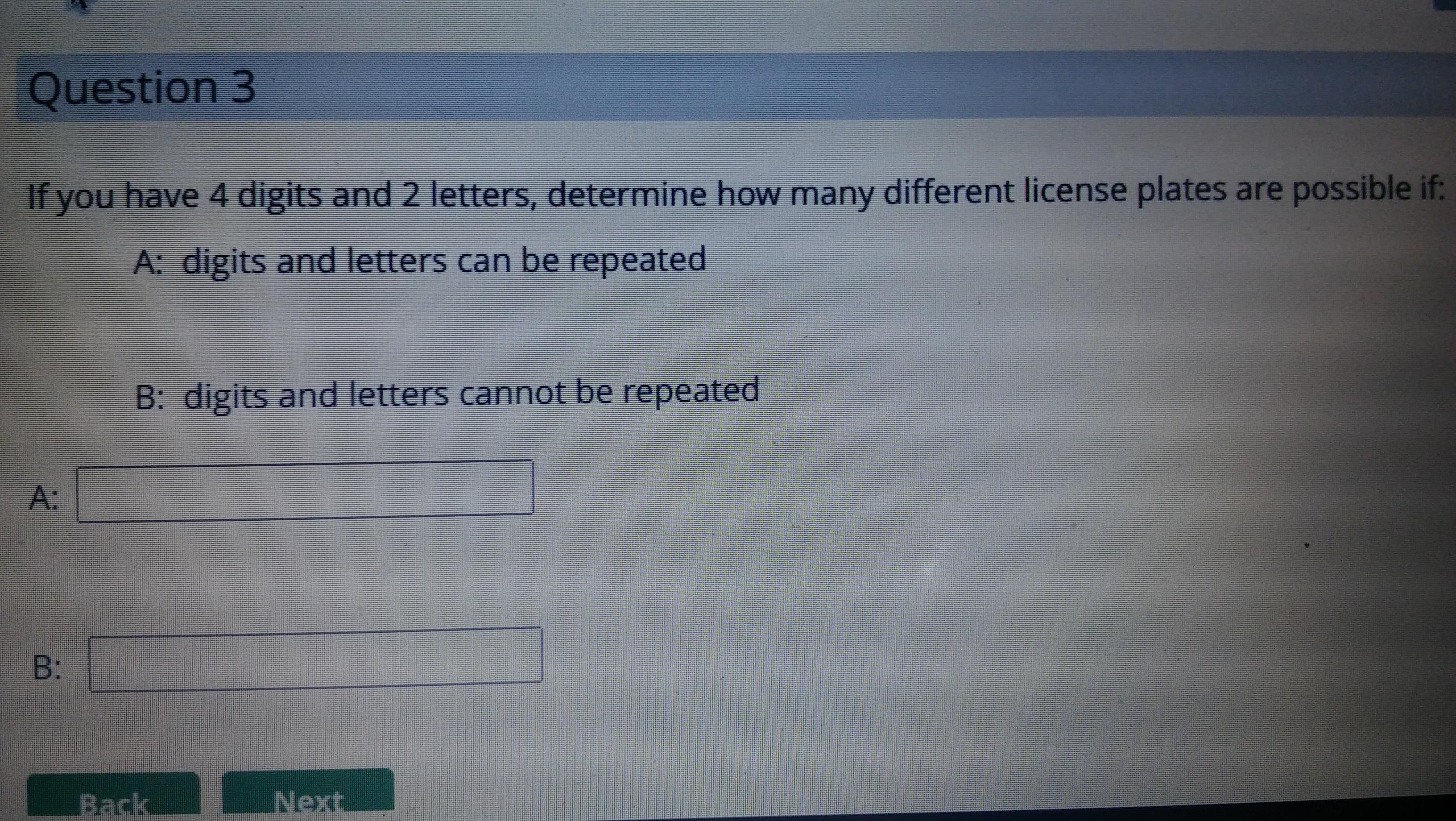
Answers
The number of different passwords, considering 2 digits and 2 letters, is given as follows:
A. 6,760,000.
B. 3,276,000.
What is the Fundamental Counting Theorem?The Fundamental Counting Theorem states that if there are m ways to do one thing and n ways to do another, then there are m x n ways to do both.
This can be extended to more than two events, where the number of ways to do all the events is the product of the number of ways to do each individual event, according to the equation presented as follows:
\(N = n_1 \times n_2 \times \cdots \times n_n\)
The password is composed by:
Four digits.Two letters.With repetition, we have that:
Each of the four digits have 10 possible outcomes.Each of the two letters have 26 possible outcomes.Hence the number of passwords is given as follows:
10^4 x 26² = 6,760,000.
Without repetition, we have that:
Digits: 10, 9, 8 and 7 outcomes.Letters: 26 and then 25 outcomes.Hence the number of passwords is given as follows:
10 x 9 x 8 x 7 x 26 x 25 = 3,276,000.
More can be learned about the Fundamental Counting Theorem at https://brainly.com/question/15878751
#SPJ1
write y+4=-2(x-1) in slope intercept form
Answers
Answer:
y=2x-6
Step-by-step explanation:
y+4=-2(x-1)
Since the slope intercept form is in the form of:
y=mx+c
Making above equation in this form.
y+4=-2(x-1)
opening bracket
y+4=2x-2
subtracting both side by 4.
y+4-4=2x-2-4
y=2x-6
This equation is the slope intercept form.
Please look at the pic and help!!

Answers
Answer:
4x² + 22x - 12
Step-by-step explanation:
A = bh/2
A = (4x - 2)(2x + 12)/2
A = (8x² + 48x - 4x - 24)/2
A = (8x² + 44x - 24)/2
A = 4x² + 22x - 12
Maya and Praisy are planting corns on a same farm. Maya plants 4 rows and Praisy plants 6 rows. If Mayas corns are ready to be picked in 8 weeks, how many weeks will it take Praisys corn to ready?
Answers
It will take 12 weeks for Praisys corn to be ready for picking.
We have been given that,
Maya plants corns In = 4 rows
Praisy plants corns in = 6 rows
Maya corns ready to be picked in = 8 weeks
We have to find the number of weeks will it take Praisys corn to be ready for picking.
To find we will use the unitary method that is,
4 rows = 8weeks
6 rows = 8/4*6 weeks
= 12 weeks
Thus 12 weeks will it take Praisys corn to be ready for picking.
Learn more about unitary method here : https://brainly.com/question/8083231
#SPJ9
Between which two integers is the value of √11 ?
O 1 and 2
O 5 and 6
O 7 and 8
O 9 and 10
O 3 and 4
Answers
Hi Student!
Looking at the question provided we are asked to find two integers. It further specifies that those two integers should be the boundaries around the number that is produced from the square root of 11.
Now that we know what the question is asking for, we can move onto answering the question. We know that \(1^2\) is equal to \(1\), \(2^2\) is equal to \(4\), \(3^2\) is equal to \(9\), and \(4^2\) is equal to \(16\). The number that was provided to us inside of the square root was 11. That means that it would be between the number 9 and 16 which is given using \(3^2\) and \(4^2\).
Therefore, the square root of 11 would be between the numbers 3 and 4. The final answer is option E, 3 and 4
A cardiac monitor is used to measure the heart rate of a patient after surgery. It compiles the number of heartbeats after t minutes. When the data in the table are graphed, the slope of the tangent line represents the heart rate in beats per minute.??t (min) 36 38 40 42 44?Heartbeats 2510 2647 2784 2915 3048??The monitor estimates this value by calculating the slope of a secant line. Use the data to estimate the patient's heart rate after 42 minutes using the secant line between the points with the given values of t. (Round your answers to one decimal place.)??
(a) t = 36 and t = 42
(b) t = 38 and t = 42
(c) t = 40 and t = 42
(d) t = 42 and t = 44
Answers
Therefore , coordinate problem solution is A) 3140 pulses per minute , B) 2915 beats per minute , C) heartbeat of 2915 beats per minute (D) or 2915.5 beats per minute .
What do coordinates mean?When locating points or other mathematical objects precisely on a region, such as Euclidean space, a coordinate system is a technique that uses one or more numbers or coordinates. Locating a point or item on a the double plane requires the use of coordinates, which are pairs of integers. Two numbers called the x and y vectors are used to define a point's location on a 2D plane. a collection of numbers that indicate specific locations.
Here,
The slope method can be used to calculate the patient's heart rhythm after 42 minutes that use the secant line connecting the points with the specified values of t:
Heartbeat change / time change is the trend.
The heart rate can then be estimated using this slope value along with the number for heartbeats at t = 42 minutes.
A)Using coordinates 36, 2510, and 42, 2915 as examples:
Cardiac rate at 42 minutes = 2510 + (42 - 36) * 75 = 3140 Slope = (2915 - 2510) / (42 - 36) = 75
b) Using coordinates (38, 2647) and (42, 2915), respectively:
Cardiac rate at 42 minutes = 2647 + (42 - 38) * 67 = 2915 Slope = (2915 - 2647) / (42 - 38) = 67
c) Applying the values (40, 2784) and (42, 2915):
Heart rate at 42 minutes = 2784 + (42 - 40) * 65.5 = 2915.5 Slope = (2915 - 2784) / (42 - 40) = 65.5
Using coordinates (42, 2915), and (44, 3048), respectively:
Cardiac rate at 42 minutes = 2915 + (42 - 42) * 66.5 = 2915 Slope: (3048 - 2915) / (44 - 42) = 66.5
To know more about coordinates visit:
https://brainly.com/question/27749090
#SPJ4
a company makes carboard cylindrical boxes with a diameter of 10 inches and a height of 8 inches.how many square inches of carboard are needed for each box? Use 3.14 for pi.
Answers
Answer:
408.2sq inches
Step-by-step explanation:
Area of the cylindrical box = 2πr(r+h)
r is the radius = diameter/2
r = 10/2 = 5in
h is the height = 8in
Substitute
Area of the cylindrical box = 2(3.14)(5)(5+8)
Area of the cylindrical box = 2 * 3.14 * 5 * 13
Area of the cylindrical box = 408.2sq inches
What is the domain of this function ?

Answers
At the beginning of spring, Robert planted a small sunflower in his backyard. When it
was first planted, the sunflower was 5 inches tall. The sunflower then began to grow
at a rate of 3 inches per week. How tall would the sunflower be after 10 weeks? How
tall would the sunflower be after w weeks?
Height after 10 weeks:
Height after w weeks:
I need help fast
