Collect like terms y + 2 y
Answers
Answer:
y + 2y = 3y
Explanation:
y and 2y are like terms. Their sum is 3y
Related Questions
this is worth 40 points so pls help! I need this ASAP.
I also need COMPLETE solution


Answers
Answer:
Shown below.
Step-by-step explanation:
Test Marks Tally Frequency Percentage
1 8 8/60 = 0.133
2 6 6/60 = 0.100
3 5 5/60 = 0.083
4 5 5/60 = 0.083
5 5 5/60 = 0.083
6 8 8/60 = 0.133
7 6 6/60 = 0.100
8 7 7/60 = 0.116
9 4 4/60 = 0.066
10 5 5/60 = 0.083
Total 59 59/60 = 0.983
For the Tally section, I believe you just fill in tally marks corresponding to the frequency. One of the observations in the table is 0, which is not a column in the frequency table.
(1) is € 7 is in {7}? yes no
(2) how many elements are in the set {7, 7, 7, 7, 7, 7}?
(3) how many elements are in the set {0, {0}}?
(4) is {0} € is in {{0}, {1}}? yes no
(5) is 0 € is in {{0}, {1}}? yes no
Answers
(1) No, €7 is not an element of the set {7}.
(2) There is only one element in the set {7, 7, 7, 7, 7, 7}.
(3) There are two elements in the set {0, {0}}.
(4) No, {0} is not an element of the set {{0}, {1}}.
(5) Yes, 0 is an element of the set {{0}, {1}}.
(1) The set {7} contains only the element 7, so €7, which represents the currency Euro, is not an element of this set.
(2) In the set {7, 7, 7, 7, 7, 7}, all the elements are the same, namely 7. Therefore, there is only one distinct element in this set.
(3) The set {0, {0}} contains two elements: 0 and the set {0}. The element {0} is considered distinct from the numerical value 0, so they are counted as separate elements.
(4) The set {{0}, {1}} contains two elements: the set {0} and the set {1}. The element {0} is not the same as the set {0}, so {0} is not an element of the set {{0}, {1}}.
(5) The number 0 is an element of the set {{0}, {1}} because it is one of the values present in the set. Therefore, 0 is an element of the set.
Learn more about numerical here:
https://brainly.com/question/32564818
#SPJ11
In a sample of 1000 U.S. adults, 150 said they are very confident in the nutritional information on restaurant menus. Four U.S adults are selected at random without replacement (a) Find the probability that all four adults are very confident in the nutritional information on restaurant menus (b) Find the probability that none of the four adults are very confident in the nutritional information on restaurant menus 0.522 (c) Find the probability that at least one of the four adults is very confident in the nutritional information on restaurant menus 0.478
Answers
(a)The probability that all four adults are very confident is approximately 0.0056.
(b) The probability that none of the adults are very confident is approximately 0.522.
(c) The probability that at least one adult is very confident is approximately 0.478.
What is the probability of selecting four adults at random without replacement from a sample of 1000 U.S. adults, given the proportion of very confident individuals?
The probability of selecting four adults at random without replacement from a sample of 1000 U.S. adults depends on the proportion of very confident individuals. By calculating the probability of all four adults being very confident (a), none of the four adults being very confident (b), and at least one of the four adults being very confident (c), we can determine the likelihood of these scenarios occurring based on the given information.
To solve this problem, we can use the concept of probability and combinations.
(a)Given that there are 150 out of 1000 U.S. adults who are very confident, the probability of selecting one adult who is very confident is:
P(very confident) = 150/1000
= 0.15
Since the sampling is done without replacement, after each selection, the sample size decreases by 1. Therefore, for the second selection, the probability becomes 149/999, for the third selection, it becomes 148/998, and for the fourth selection, it becomes 147/997.
To find the probability that all four adults are very confident, we multiply these probabilities together:
P(all four adults are very confident) = (0.15) * (149/999) * (148/998) * (147/997)
≈ 0.0056
(b) The probability of selecting one adult who is not very confident (opposite of very confident) is:
P(not very confident) = 1 - P(very confident)
= 1 - 0.15
= 0.85
Since we are selecting four adults at random without replacement, the probability of none of them being very confident can be calculated as:
P(none very confident) = P(not very confident) * P(not very confident) * P(not very confident) * P(not very confident)
= (0.85)* (0.85) * (0.85) * (0.85)
≈ 0.522
(c) The probability of at least one adult being very confident is the complement of none of them being very confident:
P(at least one very confident) = 1 - P(none very confident)
= 1 - 0.522
= 0.478
Therefore,
(a) The probability that all four adults are very confident is approximately 0.0056.
(b) The probability that none of the adults are very confident is approximately 0.522.
(c) The probability that at least one adult is very confident is approximately 0.478.
To learn more about the probability from the given link
brainly.com/question/13604758
#SPJ4
Rewrite the piece-wise function f(t) in terms of a unit step function. b) Compute its Laplace transform. 12, 0≤1<4 f(t)= 3t, 4≤1<6 18, 126
Answers
The piece-wise function f(t) in terms of a unit step function. b) Compute its Laplace transform L{f(t)} = 12/s + 3 * [e^(-4s) * (1/s^2) * (1 - e^(-4s)) - e^(-6s) * (1/s^2) * (1 - e^(-6s))] + 18 * e^(-6s) * (1/s^2)
To rewrite the piece-wise function f(t) in terms of a unit step function, we can use the unit step function u(t). The unit step function is defined as follows:
u(t) = 0, t < 0
u(t) = 1, t ≥ 0
Now let's rewrite the piece-wise function f(t) using the unit step function:
f(t) = 12u(t) + 3t[u(t-4) - u(t-6)] + 18u(t-6)
Here's the breakdown of the expression:
- The first term, 12u(t), represents the value 12 for t greater than or equal to 0.
- The second term, 3t[u(t-4) - u(t-6)], represents the linear function 3t for t between 4 and 6, where the unit step function u(t-4) - u(t-6) ensures that the function is zero outside that interval.
- The third term, 18u(t-6), represents the value 18 for t greater than or equal to 6.
Now, let's compute the Laplace transform of f(t). The Laplace transform is denoted by L{ } and is defined as:
L{f(t)} = ∫[0, ∞] f(t)e^(-st) dt,
where s is the complex frequency parameter.
Applying the Laplace transform to the expression of f(t), we have:
L{f(t)} = 12L{u(t)} + 3L{t[u(t-4) - u(t-6)]} + 18L{u(t-6)}
The Laplace transform of the unit step function u(t) is given by:
L{u(t)} = 1/s.
To find the Laplace transform of the term 3t[u(t-4) - u(t-6)], we can use the time-shifting property of the Laplace transform, which states that:
L{t^n * f(t-a)} = e^(-as) * F(s),
where F(s) is the Laplace transform of f(t).
Applying this property, we obtain:
L{t[u(t-4) - u(t-6)]} = e^(-4s) * L{t*u(t-4)} - e^(-6s) * L{t*u(t-6)}.
The Laplace transform of t*u(t-a) is given by:
L{t*u(t-a)} = (1/s^2) * (1 - e^(-as)).
Therefore, we have:
L{t[u(t-4) - u(t-6)]} = e^(-4s) * (1/s^2) * (1 - e^(-4s)) - e^(-6s) * (1/s^2) * (1 - e^(-6s)).
Finally, substituting these results into the Laplace transform expression, we obtain the Laplace transform of f(t):
L{f(t)} = 12/s + 3 * [e^(-4s) * (1/s^2) * (1 - e^(-4s)) - e^(-6s) * (1/s^2) * (1 - e^(-6s))] + 18 * e^(-6s) * (1/s^2).
Please note that the Laplace transform depends on the specific values of s, so further simplification or evaluation of the expression may be required depending on the desired form of the Laplace transform.
To learn more about "Laplace transform" refer here:
https://brainly.com/question/29583725
#SPJ11
Use Black-Scholes model to determine the price of a European call option. Assume that S0 = $50, rf = .05, T = 6 months, K = $55, and σ = 40%. Please show all work. Please use four decimal places for all calculations.
Answers
The price of a European call option can be determined using the Black-Scholes model. Given the parameters S0 = $50, rf = 0.05, T = 6 months, K = $55, and σ = 0.40, the calculated price of the option is $2.2745.
The Black-Scholes model is used to calculate the price of a European call option based on various parameters. The formula for the price of a European call option is:
C = S0 * N(d1) - K * e^(-rf * T) * N(d2)
Where:
C is the price of the call option
S0 is the current price of the underlying asset
N() represents the cumulative standard normal distribution function
d1 = (ln(S0 / K) + (rf + (σ^2)/2) * T) / (σ * sqrt(T))
d2 = d1 - σ * sqrt(T)
Using the given parameters, we can calculate the values of d1 and d2. Then, we use these values along with the other parameters in the Black-Scholes formula to calculate the price of the option. Substituting the given values into the formula, we have:
d1 = (ln(50 / 55) + (0.05 + (0.40^2)/2) * (0.5)) / (0.40 * sqrt(0.5)) = -0.3184
d2 = -0.3184 - (0.40 * sqrt(0.5)) = -0.6984
Next, we calculate N(d1) and N(d2) using the cumulative standard normal distribution table or a calculator. N(d1) ≈ 0.3745 and N(d2) ≈ 0.2433.
Plugging these values into the Black-Scholes formula, we get:
C = 50 * 0.3745 - 55 * e^(-0.05 * 0.5) * 0.2433 = $2.2745
Therefore, the calculated price of the European call option is approximately $2.2745.
Learn more about Black-Scholes model here:
https://brainly.com/question/32940416
#SPJ11
The length of a rectangle is five centimeters less than four times the width. If the perimeter id 50cm, find the width and length.
Answers
Answer:
W is 6
L is 19
Step-by-step explanation:
L= 4W - 5
P= 2L + 2W
P= 2(4W-5) +2W
50=8W -10 +2W
60 = 10W
W= 6
L= 19
What is m
A:55°
B: 110°
C:125°
D:235°

Answers
at 2:00pm a car's speedometer reads and at 2:10pm it reads use the mean value theorem to find an acceleration the car must achieve.
Answers
The car must achieve an acceleration of 120 mi/h² at some point between 2:00pm and 2:10 pm.
To find the acceleration the car must achieve using the Mean Value Theorem (MVT), we need to follow these steps:
1. Calculate the change in speed.
2. Calculate the change in time.
3. Apply the MVT to find the acceleration.
Step 1: The car's speedometer reads 50mph at 2:00 pm and 70mph at 2:00 pm. The change in speed is 70mph - 50mph = 20mph.
Step 2: The change in time is 10 minutes, which we need to convert to hours. To do this, divide 10 by 60 (since there are 60 minutes in an hour). So, 10/60 = 1/6 hour.
Step 3: Apply the MVT. The MVT states that there must be a point in time where the average acceleration equals the instantaneous acceleration. The average acceleration (a) can be found using the formula a = Δv/Δt. Here, Δv is the change in speed (20mph) and Δt is the change in time (1/6 hour).
So, a = (20mph) / (1/6 hour) = 20 * 6 = 120 mi/h².
Learn more about speedometer: https://brainly.com/question/27340138
#SPJ11
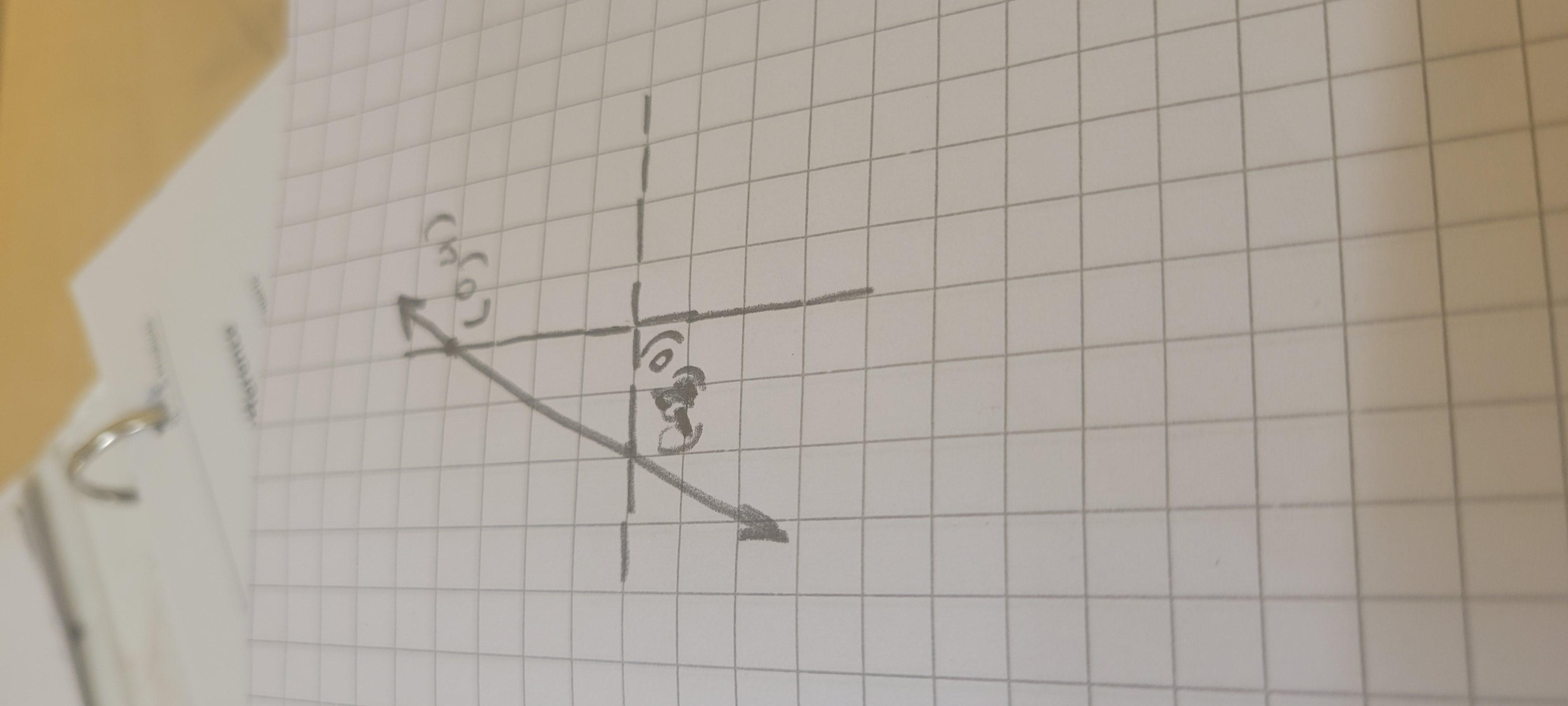
Graph the following line (-2,0) and (0,4)
Answers
Sorry if image is not
In ΔPQR, \overline{PR} PR is extended through point R to point S, \text{m}\angle QRS = (10x-1)^{\circ}m∠QRS=(10x−1) ∘ , \text{m}\angle RPQ = (3x+17)^{\circ}m∠RPQ=(3x+17) ∘ , and \text{m}\angle PQR = (2x+12)^{\circ}m∠PQR=(2x+12) ∘ . Find \text{m}\angle QRS.M∠QRS.
Answers
Answer:
<QRS = 55 degrees
Step-by-step explanation:
Given the following
m∠QRS=(10x−1) ∘
∠RPQ=(3x+17) ∘
m∠PQR=(2x+12)
External angle m<QRS = 10x-1
Interior angles are m∠RPQ=(3x+17) ∘ and m∠PQR=(2x+12)
Using the law that the sum of interior angle is equal to exterior
10x + 1 = 3x+17 + 2x + 12
10x+1 = 5x+29
10x-5x = 29-1
5x = 28
x = 28/5
x = 5.6
Get m<QRS
Recall that <QRS = 10x - 1
<QRS = 10(5.6) - 1
<QRS = 56-1
<QRS = 55 degrees
find n 3ft area=33 sq ft
Answers
The dimensions of the rectangle are 6 ft by 5.5 ft, and n = 6.
What is the area of the rectangle?
To find the area of a rectangle, we multiply the length of the rectangle by the width of the rectangle.
We know that the area of a rectangle is given by:
Area = Length x Width
Since the problem does not specify the shape of the rectangle, we cannot assume that it is a square. Therefore, we need to find two numbers whose product is 33.
The factors of 33 are 1, 3, 11, and 33. None of these factors is equal to 3, so we cannot simply multiply 3 by a factor of 33 to get the length of the rectangle. Therefore, we need to use a different approach.
One way to find two numbers whose product is 33 is to start with the square root of 33 and round up and down to the nearest integer. The two resulting integers will be close to the factors of 33 and will multiply to give 33.
The square root of 33 is approximately 5.74. Rounding up and down to the nearest integer gives:
Length = 6 ft
Width = 33 ÷ 6 = 5.5 ft (approximately)
The product of these two numbers is:
6 ft x 5.5 ft ≈ 33 sq ft
Therefore, the dimensions of the rectangle are 6 ft by 5.5 ft, and n = 6.
To learn more about the area of the rectangle visit:
brainly.com/question/2607596
#SPJ1
if 1/3 of taffy cost $2.10 how much is one pound of taffy?
Answers
Answer:
$6.30
Step-by-step explanation:
since 1/3 is considered 1/3 of a pound, you can multiply 2.10 by 3.
2.10 x 3 = 6.30
Answer:
$6.30
Step-by-step explanation:
3 × 2.10 = 6.30
You know you got the question right if you divide 6.30 by 3 because it's 1/3
PLEASE HELP WORTH 15 POINTS

Answers
$22.00+$14.00=
answer this
Answers
Answer:
$36
Step-by-step explanation:
22+14=36
Identify if equations are functions or not functions (see photo) sort them out please

Answers
Answer:
B AND B Because they are the only awnsers that make grammatical sense.
PLS HELP ASAP I WILL GIVE BRAINLIEST!!!!
An isosceles triangle (that is a triangle with 2 equal sides and a base of a different length) has a base of 5 centimeters and the other two sides are x centimeters long. The perimeter is no more than 30 centimeters. Write and solve the inequality to find the possible values of x.
Follow this form
77x > 154 ; x > 2
Answers
5 + 2x ≤ 30
2x ≤ 25
x ≤ 12.5
Did this help? I hope it did! Pls tell me if it helped!
it can be shown that y1=e3x and y2=e−7x are solutions to the differential equation y′′ 4y′−21y=0 on the interval (−[infinity],[infinity]). find the wronskian of y1,y2 (note the order matters)
Answers
The Wronskian of y1 = e^(3x) and y2 = e^(-7x) on the interval (-∞, ∞) is W(y1, y2) = 10.
To find the Wronskian of y1 = e^(3x) and y2 = e^(-7x), we can use the formula for calculating the Wronskian of two functions. Let's denote the Wronskian as W(y1, y2).
The formula for calculating the Wronskian of two functions y1(x) and y2(x) is given by:
W(y1, y2) = y1(x) * y2'(x) - y1'(x) * y2(x)
Let's calculate the derivatives of y1 and y2:
y1(x) = e^(3x)
y1'(x) = 3e^(3x)
y2(x) = e^(-7x)
y2'(x) = -7e^(-7x)
Now, substitute these values into the Wronskian formula:
W(y1, y2) = e^(3x) * (-7e^(-7x)) - (3e^(3x)) * e^(-7x)
= -7e^(3x - 7x) - 3e^(3x - 7x)
= -7e^(-4x) - 3e^(-4x)
= (-7 - 3)e^(-4x)
= -10e^(-4x)
So, the Wronskian of y1 = e^(3x) and y2 = e^(-7x) is W(y1, y2) = -10e^(-4x).
Note that the order of the functions matters in the Wronskian calculation. If we were to reverse the order and calculate W(y2, y1), the result would be the negative of the previous Wronskian:
W(y2, y1) = -W(y1, y2) = 10e^(-4x).
Since the Wronskian is a constant value regardless of the interval (-∞, ∞) in this case, we can evaluate it at any point. For simplicity, let's evaluate it at x = 0:
W(y1, y2) = 10e^(0)
= 10
Therefore, the Wronskian of y1 = e^(3x) and y2 = e^(-7x) on the interval (-∞, ∞) is W(y1, y2) = 10.
Learn more about interval here
https://brainly.com/question/30354015
#SPJ11
In a court case, a judge cited a court of contempt and ordered a fine of $2 for first day. On subsequent days, the fine would be equal to the square of the previous day's fine. e.g. 2, 4, 16, 256 and so on. Find out:-
a) What would be the fine on day n
?
b) How many days would it take the fine to reach D
dollars?
Answers
Using geometric sequence, a) The fine on day n is $2^n (2 to the power of n). b) It would take log_2(D/2) + 1 days for the fine to reach D dollars.
In this court case, the fine on each subsequent day is equal to the square of the previous day's fine. This means that the fine follows a geometric sequence, where the common ratio is the square of the previous term.
a) To find the fine on day n, we can use the formula for the nth term of a geometric sequence:
a_n = a_1 * r^(n-1)
Where a_n is the nth term, a_1 is the first term, r is the common ratio, and n is the term number.
In this case, a_1 = 2 (the fine on the first day), r = 2 (the common ratio), and n is the day number. Plugging these values into the formula, we get:
a_n = 2 * 2^(n-1)
So the fine on day n would be 2 * 2^(n-1) dollars.
b) To find how many days it would take the fine to reach D dollars, we can use the formula for the nth term of a geometric sequence and solve for n:
D = 2 * 2^(n-1)
Dividing both sides by 2, we get:
D/2 = 2^(n-1)
Taking the logarithm of both sides with base 2, we get:
log_2(D/2) = n - 1
Adding 1 to both sides, we get:
n = log_2(D/2) + 1
So it would take log_2(D/2) + 1 days for the fine to reach D dollars.
Know more about geometric sequence here:
https://brainly.com/question/24643676
#SPJ11
Each person who applies for an assembly job at Robert's Electronics is given a mechanical aptitude test. One part of the test involves assembling a plug-in unit based on numbered instructions. A sample of the length of time it took 42 persons to assemble the unit was organized into the following frequency distribution. Length of Time (in minutes) Number 1 up to 4 4 4 up to 7 8 7 up to 10 14 10 up to 13 9 13 up to 16 5 16 up to 19 2 What is the mean (in minutes)
Answers
The mean in minutes of the length of time given= 9.1
Calculation of mean when frequency table is givenThe formula used for the determination of mean when a frequency table is given is
= total/n
Where total = frequency×midpoint
n = 42
To calculate the total, the mid point of each length of time is determined as follows;
1+4/2 = 2.5 × 4 = 10
4+7/2= 5.5 × 8 = 44
7+10/2 = 8.5 × 14= 119
10+13/2 = 11.5× 9 = 103.5
13+16/2= 14.5×5 = 72.5
16+19/2= 17.5× 2= 35
Total= 10+44+119+103.5+72.5+35 = 384
Therefore mean = 384/42= 9.1
Learn more about mean here:
https://brainly.com/question/20118982
#SPJ1

Which number is closest to √52?
Answers
Answer:
7
Step-by-step explanation:
Answer:
√52 = 2√13
Step-by-step explanation:
is 0.725 a repeating decimal
Answers
Answer:
No it is not a repeating decimal.
Step-by-step explanation:
It is not a repeating decimal because you can see that it stops and it does not have a repeating sign which is a line above the numbers after the decimal.
is 47°, what is the measure of Z3?
Ο Α. 1536
O B. 43
O C. 133
O D. 47°

Answers
Answer:
<3=C. 133
Step-by-step explanation:
Well, angle 2 and angle 3 are corrisponding angles, meaning that they are on the same line, and a line is always equal to 180, and 47 degrees is a part of that line, and you need the other part of that line for angle 3, so you simply subtract 180-47=133 degrees
show work needed with this question!

Answers
Answer:
The final value is 8750
Step-by-step explanation:
First step is to find the increase
3500 * 150%
3500 * 1.5
5250
Now we need to add the increase to the starting value
3500 + 5250
8750
The final value is 8750
write a quadratic function h whose only zero is 5
h(x)=
Answers
well, is a quadratic, so it has two roots, in this case that'll be 5 only per se, is really 5 but twice, or we should say it has a root of 5 with multiplicity of 2, that gives us
\(\begin{cases} x = 5 &\implies x -5=0\\ x = 5 &\implies x -5=0\\ \end{cases} \\\\[-0.35em] ~\dotfill\\\\ \stackrel{original~polynomial}{a ( x -5 )( x -5 ) = \stackrel{0}{h}}\hspace{5em}\stackrel{\textit{assuming}}{a=1}\hspace{5em}1(x-5)(x-5)=h(x) \\\\\\ ~\hfill {\Large \begin{array}{llll} x^2-10x+25=h(x) \end{array}}~\hfill\)
The proportion of a normal distribution located between z = .50 and z = -.50 is ____.
Answers
The proportion of a normal distribution located between z = .50 and z = -.50 will be 38.2%.
We have,
A normal distribution located between z = 0.50 and z = -0.50,
So,
Now,
From the Z-score table,
We get,
The Probability corresponding to the Z score of -0.50,
i.e.
P(-0.50 < X < 0) = 0.191,
And,
The Probability corresponding to the Z score of -0.50,
i.e.
P(0 < X < 0.50) = 0.191,
Now,
The proportion of a normal distribution,
i.e.
P(Z₁ < X < Z₂) = P(Z₁ < X < 0) + P(0 < X < Z₂)
Now,
Putting values,
i.e.
P(-0.50 < X < 0.50) = P(-0.50 < X < 0) + P(0 < X < 0.50)
Now,
Again putting values,
We get,
P(-0.50 < X < 0.50) = 0.191 + 0.191
On solving we get,
P(-0.50 < X < 0.50) = 0.382
So,
We can write as,
P(-0.50 < X < 0.50) = 38.2%
So,
The proportion of a normal distribution is 38.2%.
Hence we can say that the proportion of a normal distribution located between z = .50 and z = -.50 will be 38.2%.
Learn more about normal distribution here
https://brainly.com/question/13759327
#SPJ4
plz plz plz help me worth 20 paints and will give brainlyist plz help me!!!!!!!
Question 1 (Worth 4 points)
(01.02 MC)
Scientists want to place a telescope on the moon to improve their view of distant planets. The telescope weighs 200 pounds on Earth. What will happen to the weight of the telescope when it reaches the moon?
The weight of the telescope will increase.
The weight of the telescope will decrease.
The weight of the telescope will stay the same.
The weight of the telescope will be equal to its mass.
Points earned on this question: 4
Question 2 (Worth 4 points)
(01.02 MC)
Two objects of the same mass are on two different planets. Planet A has a force of gravity that is stronger than that of Planet B. How will the weights of the objects compare to each other?
The weights of the objects will be the same.
The weight of the object on planet A will be greater than the weight of the object on planet B.
The weight of the object on planet A will be less than the weight of the object on planet B.
This cannot be determined without knowing the actual mass of the objects.
Points earned on this question: 0
Question 3 (Worth 3 points)
(01.02 LC)
What is the metric unit for mass?
Meters
Kilograms
Pounds
Matter
Points earned on this question: 3
Question 4 (Worth 3 points)
(01.02 LC)
Complete this sentence. If the force of gravity ________, the weight of an object will _______________.
decreases, increase
increases, increase
increases, stay the same
decreases, stay the same
Points earned on this question: 3
Question 5 (Worth 3 points)
(01.02 LC)
What is the force of gravity acting on an object?
Velocity
Mass
Weight
Pounds
Points earned on this question: 3
Question 6 (Worth 3 points)
(01.02 LC)
Which unit of measurement is used in the metric system?
Tons
Kilograms
Miles
Gallons
Points earned on this question: 3
Answers
Scientists want to place a telescope on the moon to improve their view of distant planets. The telescope weighs 200 pounds on Earth. What will happen to the weight of the telescope when it reaches the moon?
-The weight of the telescope will decrease.
Two objects of the same mass are on two different planets. Planet A has a force of gravity that is stronger than that of Planet B. How will the weights of the objects compare to each other?
-The weight of the object on planet A will be greater than the weight of the object on planet B.
What is the metric unit for mass?
-Kilogram
Complete this sentence. If the force of gravity ________, the weight of an object will _______________.
-increases, increase
Which unit of measurement is used in the metric system?
-Kilograms
What is the force of gravity acting on an object?
-Weight
the statement int grades[ ] = { 100, 90, 99, 80 }; is an example of
Answers
Answer:
implicit array sizing
Step-by-step explanation:
The statement "int grades[] = { 100, 90, 99, 80 };" initializes an integer array called "grades" with the values 100, 90, 99, and 80. The given statement is an example of initializing an integer array in C++.
The array is named "grades" and has an unspecified size denoted by the empty square brackets []. The values inside the curly braces { } represent the initial values of the array elements.
In this case, the array "grades" is initialized with four elements: 100, 90, 99, and 80. The first element of the array, grades[0], is assigned the value 100, the second element, grades[1], is assigned 90, the third element, grades[2], is assigned 99, and the fourth element, grades[3], is assigned 80.
The array can be accessed and manipulated using its index values. This type of initialization allows you to assign initial values to an exhibition during its declaration conveniently.
Learn more about integers here:- brainly.com/question/1768254
#SPJ11
For number one and two what are the Mean Median and Mode and Range
Please help

Answers
Answer:
median 1=41
median 2=73
Answer:
1: Mean: 53. Median: 48. Mode: There is no mode. Range: 84.
2: Mean: 57. Median: 52. Mode: No mode. Range: 63.
Hope this Helped!
200 = 1000 - n/4. What is the value of n? Show working out, please.
Answers
Answer:
n = 3200
Step-by-step explanation:
200 = 1000 - \(\frac{n}{4}\) ( subtract 1000 from both sides )
- 800 = - \(\frac{n}{4}\) ( multiply both sides by 4 to clear the fraction )
- 3200 = - n ( multiply both sides by - 1 )
n = 3200
f(x) = 3x5 – 15x3 + 12x
Answers
Answer:
f(x)=3⋅5−15⋅3+12x
Simplify each term
f(x)=15−45+12x
Subtract 45 from 15
f(x)=−30+12x