cleo can paint a room in 8 hours. while phil can paint the same room in 6 hours. if they paint the room together. how long will it take them to paint the room?
Answers
Answer:
its a fraction so it would be 3 3/7
Step-by-step explanation:
Working together, it will take Cleo and Phil 3
__
3
7
hours to paint the room.
Let x represent the number of hours it will take to paint the room while working together.
__x
8
1 __x
6
5 1
24( __x
8
1 __x
6
) 5 24(1)
3x 1 4x 5 24
7x 5 24
x 5 ___
24
7
or 3__
3
7
Related Questions
The price of a car is £21500 before it is reduced by 11%. How much does it cost after the reduction?
Can u say how u did it please
Answers
Answer: god
Step-by-step explanation:
this is easy get it right

Answers
Answer:
\(x=12\)
Step-by-step explanation:
\(y = \frac{25}{6}x-34\)
Given that,
y = 16
Now put 16 instead of y to the equation.
\(16=\frac{25x}{6}-34\)
Now solve for x.
\(16=\frac{25x}{6} -34\)
\(16+34=\frac{25x}{6}\)
\(50=\frac{25x}{6}\)
Use cross multiplication
\(50*6=25x\)
\(300=25x\)
\(\frac{300}{25} =\frac{25x}{25}\)
\(12=x\)
Hope this helps you :-)
Let me know if you have any other questions :-)
What is the slope of the line shown in the graph?
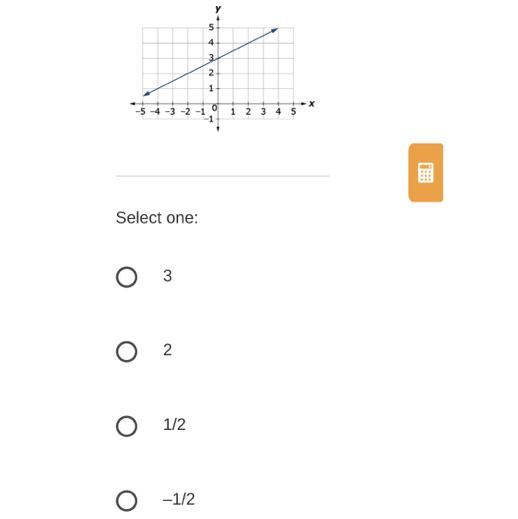
Answers
Slope=rise/run
is a number 36 a perfect square and why
Answers
Answer:
Yes it is.
Step-by-step explanation:
This is because a perfect square is the product that is given when the multiplier is multiplied by itself
The weights of Chihuahuas in a dog show
are normally distributed with a mean of 4
pounds and a standard deviation of 0.5
pound. What percentage of Chihuahuas
weigh more than 5 pounds? (Hint draw a
normal distribution)
Answers
The percentage of Chihuahuas that weigh more than 5 pounds is approximately 2.28%.
We have,
We need to find the area under the normal distribution curve to the right of the value x = 5.
We can use the standard normal distribution with a mean of 0 and a standard deviation of 1 by converting the original problem to a standard normal distribution.
z = (x - μ) / σ
where z is the standard score, x is the raw score, μ is the mean, and σ is the standard deviation.
In this case,
x = 5, μ = 4, and σ = 0.5.
z = (5 - 4) / 0.5 = 2
We can use a standard normal distribution table or calculator to find that the area to the right of z = 2 is approximately 0.0228.
Therefore,
The percentage of Chihuahuas that weigh more than 5 pounds is approximately 2.28%.
Learn more about normal distribution here:
https://brainly.com/question/31327019
#SPJ1
which of the following is equivalent to (5)^7/3? 5^-4
5^4
^7squroot5^3
^3squroot5^7
Answers
Answer:
^7 squroot5^3
Step-by-step explanation:
5x2= 10
7÷ 3= 2.5
A periodic signal is defined as x(t)= t over the interval (-TT, TT) and period TO = 21t. Sketches function over some periods. Find the trigonometric Fourier series of the function. The function is antisymmetric and therefore only the bs are different from zero. Use the integral from the integration table: St sin(at) dt = 1/a2 (sin(at) – at cos(at)] b) Create a MATLAB program that sums the first N links in the Fourier series and plot the sum above the time interval t=(-211,41). See how the result changes as a function of N. Plot finally x(t) with N = 40. Also plot the Fourier coefficients, bn, as a function of frequency, nwo. c) Also find the exponential Fourier series of the periodic function x (t). | remember that Dn =1/2 (an-jbn). Modify the MATLAB program to calculate the exponential Fourier series for x (t). Plot x (t) for N = † 40 and check that the result is the same as in point b. d) A system is defined by its transfer function given by: H(s) = 1/(s+1). function x (t) is the input signal to the system. Use the MATLAB program to calculate the output signal, y(t)=H(s)x(t), with s=jnwo. Plot y (t) for N = + 40. What happened to the signal?
Answers
a) Sketch x(t) = t., b) Compute bn coefficients., c) Calculate an coefficients., d) Obtain output signal y(t) : y(t) = H(s) * x(t).
a) The function x(t) = t over the interval (-π, π) and with a period T0 = 2π can be sketched as a linear function. b) To find the trigonometric Fourier series, we calculate the bn coefficients using the integral formula for sine terms. The bn coefficients correspond to the antisymmetric component of x(t). c) The exponential Fourier series can be obtained by using the relationship Dn = (1/2) * (an - jbn), where Dn represents the complex Fourier coefficients. We can calculate the an coefficients using the bn coefficients obtained in step b. d) The transfer function H(s) = 1/(s + 1) defines the system. By substituting s = jnω0 into H(s) and multiplying the Fourier series coefficients of x(t) with the transfer function evaluated at s = jnω0, we can calculate the output signal y(t) = H(s) * x(t) for a given value of N. Using MATLAB, we can visualize the results by varying the value of N and plotting the output signal y(t) and x(t) with N = 40.
Learn more about Fourier series and signal analysis here:
https://brainly.com/question/29672996
#SPJ11
Please help me with question 2 with explanation u will get 50 points thanks !!

Answers
If 8 people consisting of 4 couples are randomly arranged in a row, find the probability that no person is next to their partner.
Answers
The Probability that no person is next to their partner is 104/105.
Probability of an event E represented by P(E) can be defined as (The number of favorable outcomes )/(Total number of outcomes).
Permutations is defined as arrangement of elements/objects in a particular way.
According to the question ,
8 people can be arranged in 8! ways = 40320ways
First let us find the probability that person is next to their partner.
4 couples can be arranged in 4! ways
and the couple itself can be arranged in 2! ways
Since there are 4 couples ,
Number of arrangement = \(4!(2!)^{4}\)
=24x16
=384 ways
Probability that person is next to their partner = \(\frac{384}{40320} =\frac{1}{105}\)
and the probability that no person is next to their partner is \(1-\frac{1}{105} =\frac{104}{105}\).
Therefore , the probability that no person is next to their partner is \(\frac{104}{105}\).
Learn more about Probability here https://brainly.com/question/10702719
#SPJ4
13. Solve the compound inequality. 2x-62-4 and 2x-357 Graph the solution on the number line.

Answers
Answer:
bnb,j
Step-by-step explanation:
A company manufacturers and sells 2 electric drills per month. The monthly cost and price-demand equations C(x) = 72000 + 80x, p(x) = 210 - x/30, 0
Answers
The monthly cost and price-demand equations are given as C(x) = 72,000 + 80x and p(x) = 210 - x/30. Here's a step-by-step explanation using these terms.
Step 1: Determine the revenue equation.
Revenue, R(x), is calculated by multiplying the price per unit (p(x)) and the number of units sold (x). So, R(x) = x * p(x).
Step 2: Substitute the price-demand equation.
R(x) = x * (210 - x/30)
Step 3: Expand the equation.
R(x) = 210x - (x²)/30
Step 4: Find the profit equation.
Profit, P(x), is calculated by subtracting the total cost (C(x)) from the total revenue (R(x)). So, P(x) = R(x) - C(x).
Step 5: Substitute the cost and revenue equations.
P(x) = (210x - (x²)/30) - (72,000 + 80x)
Step 6: Simplify the equation.
P(x) = 210x - (x²)/30 - 72,000 - 80x
Now, you have the profit equation for the company based on the given cost and price-demand equations.
To know more about Price-demand refer here:
https://brainly.com/question/25910814
#SPJ11
Question 1
(02.01 LC)
What is the solution for the equation 4x 10 = 2x? x =______. (Input whole number
only). (5 points)
Po p
5
Answers
7=x
I hope i read the question right, but use this to help you!

find the limit of the sequence using l'hôpital's rule. bn = 4 n ln 1 1 n
Answers
limₙ→∞bₙ= 4*e^(limₙ→∞ [ln(1+1/n)/n]/[1/n^2]) = 4*e^(limₙ→∞ (1/(n*(1+n))^2)) = 4*e^(0) = 4Therefore, the limit of the sequence using L'Hospital's rule is 4.
The given sequence is bₙ = 4n ln (1 + 1/n).
To determine the limit of the sequence bₙ using L'Hospital's rule, we follow the steps given below:
Step 1: We have to find the limit of the sequence bₙ in the given form.
That islimₙ→∞bₙ= limₙ→∞[4n ln(1 + 1/n)]
Step 2: We will simplify the above expression to get an indeterminate form 0/0 using the formula n ln (1 + 1/n) = ln [(1 + 1/n)^n].Therefore, limₙ→∞bₙ= limₙ→∞[4 ln(1 + 1/n)^n] / [1/(4n)]
We can rewrite the above expression as below using the exponential function. limₙ→∞bₙ= 4 limₙ→∞ [(1 + 1/n)^n]^(4/n)
Step 3: We evaluate the limit on the right-hand side of the above equation.
It is known as e^(limₙ→∞ (4/n)*ln(1+1/n)).Therefore, limₙ→∞bₙ= 4*e^(limₙ→∞ (4/n)*ln(1+1/n))The above limit is of the form 0 * ∞.
We can apply L'Hospital's rule for this case. We take the natural logarithm of the denominator and numerator and differentiate with respect to n.
We can write the new limit as below,limₙ→∞ (4/n)*ln(1+1/n)=limₙ→∞ (ln(1+1/n)/n)/(1/n^2)
Know more about L'Hospital's rule here:
https://brainly.com/question/31398208
#SPJ11
4. Line segment CD is the perpendicular bisector of line
segment AB. Is line segment AB the perpendicular
bisector of line segment CD?

Answers
The line AB is not a perpendicular bisector of CD.
Perpendicular bisectors are lines that divides another line into two equal parts.
From the diagram, we can see that line CD cuts AB at the centre. Hence we can say that CD is a perpendicular bisector of AB.
The same is not applicable to line AB passing through CD. The line AB did not bisect (divide equally) line CD.
Hence we can conclude that line AB is not a perpendicular bisector of CD.
Learn more here: https://brainly.com/question/17335869
Random variables X and Y have joint PDF f(x,y(x,y)={
4xy
0
0≤x≤1,0≤y≤1.
otherwise.
(a) What are E[X] and Var∣X⌉ ? (b) What are E[Y] and Var[Y] ? (c) What is Cov∣X.Y∣? (d) What is E∣X+Y∣ ? (c) What is Var∣X+Y∣ ?
Answers
Given the joint probability density function (PDF) of random variables X and Y, we can calculate various statistics. The first part of the question asks for the expected value (mean) and variance of |X|, and the expected value and variance of Y. The second part asks for the covariance between |X| and Y, and the expected value and variance of |X+Y|.
(a) To calculate E[X], we integrate X multiplied by the joint PDF over the range of X and Y. Similarly, to find Var|X|, we need to calculate the variance of the absolute value of X, which requires calculating E[|X|] and E[X^2]. Using the given joint PDF, we can perform these integrations.
(b) E[Y] can be calculated by integrating Y multiplied by the joint PDF over the range of X and Y. Var[Y] can be found by calculating E[Y^2] and subtracting (E[Y])^2.
(c) The covariance between |X| and Y, denoted as Cov|X,Y|, can be calculated using the formula Cov|X,Y| = E[|X||Y|] - E[|X|]E[Y]. Again, we need to perform the necessary integrations using the given joint PDF.
(d) E[|X+Y|] can be found by integrating |X+Y| multiplied by the joint PDF over the range of X and Y.
(e) Var|X+Y| can be calculated by finding E[|X+Y|^2] - (E[|X+Y|])^2. To find E[|X+Y|^2], we integrate |X+Y|^2 multiplied by the joint PDF over the range of X and Y.
Performing these integrations using the given joint PDF will yield the specific values for each of the statistics mentioned above.
Learn more about probability density function (PDF) here: brainly.com/question/31040390
#SPJ11
You fill up your car's gas tank with $18.56 worth of gas. You pay the
cashier $20.00.
Answers
Answer:
You are left with $1.44
Step-by-step explanation:
Subtract the amount of money you payed to how much the cost actually was to get your answer.
can someone pleasee

Answers
Show that (n + 3)7 ∈ Θ(n7) for
non-negative integer n.
Proof:
Answers
To show that `(n + 3)7 ∈ Θ(n7)`, we need to prove that `(n + 3)7 = Θ(n7)`.This can be done by showing that `(n + 3)7 = O(n7)` and `(n + 3)7 = Ω(n7)` .Now, let's prove the two parts separately:
Proof for `(n + 3)7 = O(n7)`.
We want to prove that there exists a positive constant c and a non-negative constant k such that `(n + 3)7 ≤ cn7` for all `n ≥ k`.Using the Binomial theorem, we can expand `(n + 3)7` as:```
(n + 3)7
= n7 + 7n6(3) + 21n5(3)2 + 35n4(3)3 + 35n3(3)4 + 21n2(3)5 + 7n(3)6 + 37
≤ n7 + 21n6(3) + 21n5(3)2 + 35n4(3)3 + 35n3(3)4 + 21n2(3)5 + 7n(3)6 + n7
≤ 2n7 + 21n6(3) + 21n5(3)2 + 35n4(3)3 + 35n3(3)4 + 21n2(3)5 + 7n(3)6
≤ 2n7 + 84n6 + 441n5 + 2205n4 + 10395n3 + 45045n2 + 153609n + 729
```Thus, we can take `c = 153610` and `k = 1` to satisfy the definition of big-Oh notation. Hence, `(n + 3)7 = O(n7)`.Proof for `(n + 3)7 = Ω(n7)`We want to prove that there exists a positive constant c and a non-negative constant k such that `(n + 3)7 ≥ cn7` for all `n ≥ k`.Using the Binomial theorem, we can expand `(n + 3)7` as:```
(n + 3)7
= n7 + 7n6(3) + 21n5(3)2 + 35n4(3)3 + 35n3(3)4 + 21n2(3)5 + 7n(3)6 + 37
≥ n7
```Thus, we can take `c = 1` and `k = 1` to satisfy the definition of big-Omega notation. Hence, `(n + 3)7 = Ω(n7)`.
As we have proved that `(n + 3)7 = O(n7)` and `(n + 3)7 = Ω(n7)`, therefore `(n + 3)7 = Θ(n7)`.Thus, we have shown that `(n + 3)7 ∈ Θ(n7)`.From the proof, we can see that we used the Binomial theorem to expand `(n + 3)7` and used algebraic manipulation to bound it from above and below with suitable constants. This technique can be used to prove the time complexity of various algorithms, where we have to find the tightest possible upper and lower bounds on the number of operations performed by the algorithm.
Hence, we have shown that `(n + 3)7 ∈ Θ(n7)` for non-negative integer n.
To know more about Binomial theorem :
brainly.com/question/30095070
#SPJ11
Enter your answer and show all the steps that you use to solve this problem in the space provided.
What is the value of x?

Answers
Answer:
I guess 342 is the answer.
Step-by-step explanation:
Because the sum of all angles of a ️(triangle) is 360 degree.
Answer:
Step-by-step explanation:
(isosceles triangle base angles are equal)
(all angles of triangle are equal to 180)
38 + x + x = 180
2x = 180 - 38
2x/2 = 142/2
x = 71
help please ineed this

Answers
Answer:
(3,1)
Step-by-step explanation:
6) y = -5(x + 7)
Is it linear
Answers
Answer:yes
Step-by-step explanation:
It has the y=mx+b format
cosA/secA+sinA/cosecA=1
Answers
Step-by-step explanation:
please mark me as brainlest

Both Fred and Ed have a bag of candy containing a lemon drop, a cherry drop, and a lollipop. Each takes out a piece and eats it. What are the possible pairs of candies eaten? A. Lemon-lemon, cherry-lemon, lollipop-lollipop, lemon-cherry, cherry-cherry, lemon-lollipop, lollipop-cherry, cherry-lollipop, lollipop-lemon B. Cherry-lemon, lemon-lollipop, lollipop-cherry, lollipop-lollipop, lemon-lemon C. Lemon-cherry, lemon-cherry, lemon-cherry, lemon-lollipop, lemon-lollipop, lemon-lollipop, cherry-lollipop, cherry-lollipop, cherry-lollipop D. Lemon-lemon, cherry-lemon, lollipop-lollipop, lemon-lollipop, cherry-cherry, lemon-lollipop, lollipop-cherry, cherry-lemon, lollipop-lemon
Answers
Answer:
A. Lemon-lemon, cherry-lemon, lollipop-lollipop, lemon-cherry, cherry-cherry, lemon-lollipop, lollipop-cherry, cherry-lollipop, lollipop-lemon
Step-by-step explanation:
From the above question, we are told that both Fred and Ed have a bag of candy containing a lemon drop, a cherry drop, and a lollipop
There are two events here's
2 people = Fred and Ed
3 bags of different sweets = Lemon Cherry and Lollipop
The number of ways that both of them can eat this singly is calculated using combination formula
C(n, r) = nCr = n!/r! (n - r)!
n = 3, r = 2 = 3C2 = 3!/2! (3 - 2)!
= 3 × 2 × 1/2 × 1
= 3
We were asked to find the possible pairs
Hence = 3² = 9
There are 9 possible pairs through which Fred and Ed can eat their sweets and they are:
1) Lemon - Lemon
2) Cherry - Cherry
3) Lollipop - Lollipop
4) Lemon - Cherry
5) Cherry - Lemon
6) Lollipop - Cherry
7) Cherry - Lollipop
8) Lollipop - Lemon
9) Lemon - Lollipop.
Therefore, Option A is the correct option
Answer:
LEMONS BURN YOUR HOUSE DOWN JK its this A. Lemon-lemon, cherry-lemon, lollipop-lollipop, lemon-cherry, cherry-cherry, lemon-lollipop, lollipop-cherry, cherry-lollipop, lollipop-lemon
Step-by-step explanation:
From the above question, we are told that both Fred and Ed have a bag of candy containing a lemon drop, a cherry drop, and a lollipop
There are two events here's
2 people = Fred and Ed
3 bags of different sweets = Lemon Cherry and Lollipop
The number of ways that both of them can eat this singly is calculated using combination formula
C(n, r) = nCr = n!/r! (n - r)!
n = 3, r = 2 = 3C2 = 3!/2! (3 - 2)!
= 3 × 2 × 1/2 × 1
= 3
We were asked to find the possible pairs
Hence = 3² = 9
There are 9 possible pairs through which Fred and Ed can eat their sweets and they are:
1) Lemon - Lemon
2) Cherry - Cherry
3) Lollipop - Lollipop
4) Lemon - Cherry
5) Cherry - Lemon
6) Lollipop - Cherry
7) Cherry - Lollipop
8) Lollipop - Lemon
9) Lemon - Lollipop.
Therefore, Option A is the correct option
please help i need help

Answers
-1 3/4
-2
3.5
4 1/2
a function satisfies the differential equation (a) what are the constant solutions of this equation? separate your answers by commas.
Answers
The solutions are decreasing when y is in the set (1,3).
(A) Equilibrium solutions, also known as constant solutions, fulfill dy/dx=0.
When the right-hand side of the equation is taken into account, we have
dy/dx equals y2(y-1) (y-3). We get the constant solutions y=0, y=1, and y=3 by setting the right side to zero.
(b) Solutions rise when dy/dx exceeds 0. For the set of y values (-,0) (0,1) (3,) see that dy/dx > 0. Therefore, when y in is the set (-,0) (0,1) (3,), solutions are growing.
(c) When dy/dx 0, solutions are decreasing, and dy/dx 0 when 1 y 3. That is, while y is in the set, solutions are decreasing (1,3).
Know more about differential equation
https://brainly.com/question/1164377
#SPJ4
Help needed desperately

Answers
Answer:
80° , 100°, 80°
Step-by-step explanation:
∠ 1 and ∠ 2 form a straight line and sum to 180° , then
2x + 40 + 2y + 40 = 180
2x + 2y + 80 = 180 ( subtract 80 from both sides )
2x + 2y = 100 → (1)
∠ 1 and ∠ 3 are vertical angles and are congruent , then
2x + 40 = x + 2y ( subtract x from both sides )
x + 40 = 2y ( subtract 40 from both sides )
x = 2y - 40 → (2)
Substitute x = 2y - 40 into (1)
2(2y - 40) + 2y = 100
4y - 80 + 2y = 100
6y - 80 = 100 ( add 80 to both sides )
6y = 180 ( divide both sides by 6 )
y = 30
Substitute y = 30 into (2)
x = 2(30) - 40 = 60 - 40 = 20
Thus x = 20 and y = 30
Then
∠ 1 = 2x + 40 = 2(20) + 40 = 40 + 40 = 80°
∠ 2 = 2y + 40 = 2(30) + 40 = 60 + 40 = 100°
∠3 = x + 2y = 20 + 2(30) = 20 + 60 = 80°
Which of the following is a Platonic solid?
A torus
B. sphere
C. tetrahedron
D. cylinder
Answers
Answer:
c. tetrahedron
Step-by-step explanation:
Pierre correctly simplified an expression. When he substituted x = 2 into the simplified expression, the value was 20. Which could be Pierre’s original expression?
2(7x – 4)
2(x – 19)
2(x + 10)
2(5x + 1)
Answers
Answer:2(7x-4)
Step-by-step explanation:
Answer:
The correct answer is A.) 2(7x – 4)
Step-by-step explanation:
I just did the test and got it right
Mr.Elms Can run 20 miles per hour; but he can only run for 4 hours. What’s the domain and range?
Answers
Mr. Elms can only run for four hours, his range and domain are each set at 20 miles per hour.
what is domain ?A function's acceptable range of values is referred to as its domain. These numbers serve as representations of the x-values of a function like f. (x). The set of potential values that a function can be applied to is known as its domain. When the x value is inserted, the method returns the value that is contained in this set. A function's definition is Y = f, where x is the independent variable and y is the dependent variable (x). If it is possible to successfully use a value of x to generate a single value of y using the value of x, that value of x is said to be in the domain of the function.
given
Graphs can be used as a second method to define the domain and range of functions.
A graph's domain is the entire set of input values represented on the x-axis because the term "domain" refers to the set of potential input values. The various output values are displayed on the y-axis and make up the range.
To know more about domain visit:
https://brainly.com/question/28135761
#SPJ1
Simplify (2a²b⁵)(-3ab-⁴)
help.
Answers
Answer:
-6a\(x^{3\)b\(x^{6}\) - 8a\(x^{2}\)b\(x^{5}\)
Step-by-step explanation: