Circle C is shown. Line segments E C and C D are radii. Lines are drawn from points E and D to point F on the other side of the circle. Arc E D measures 95 degrees. What is the measure of angle EFD? 37.5° 45° 47.5° 55°
Answers
Answer:
(C)\(47.5^\circ\)
Step-by-step explanation:
In the circle, the measure of arc ED is the measure of an angle subtended by arc ED at the centre.
Angle EFD on the other hand is an angle subtended by arc ED on the circumference.
We have a circle's theorem that states:
The angle subtended by the arc at the centre is twice the angle subtended by the same arc at the circumference, therefore:
\(m\angle ED=2 \times m\angle EFD\\95^\circ=2 \times m\angle EFD\\m\angle EFD=95 \div 2\\m\angle EFD=47.5^\circ\)
Answer:
its 47.5
Step-by-step explanation:
i got it right on edge
Related Questions
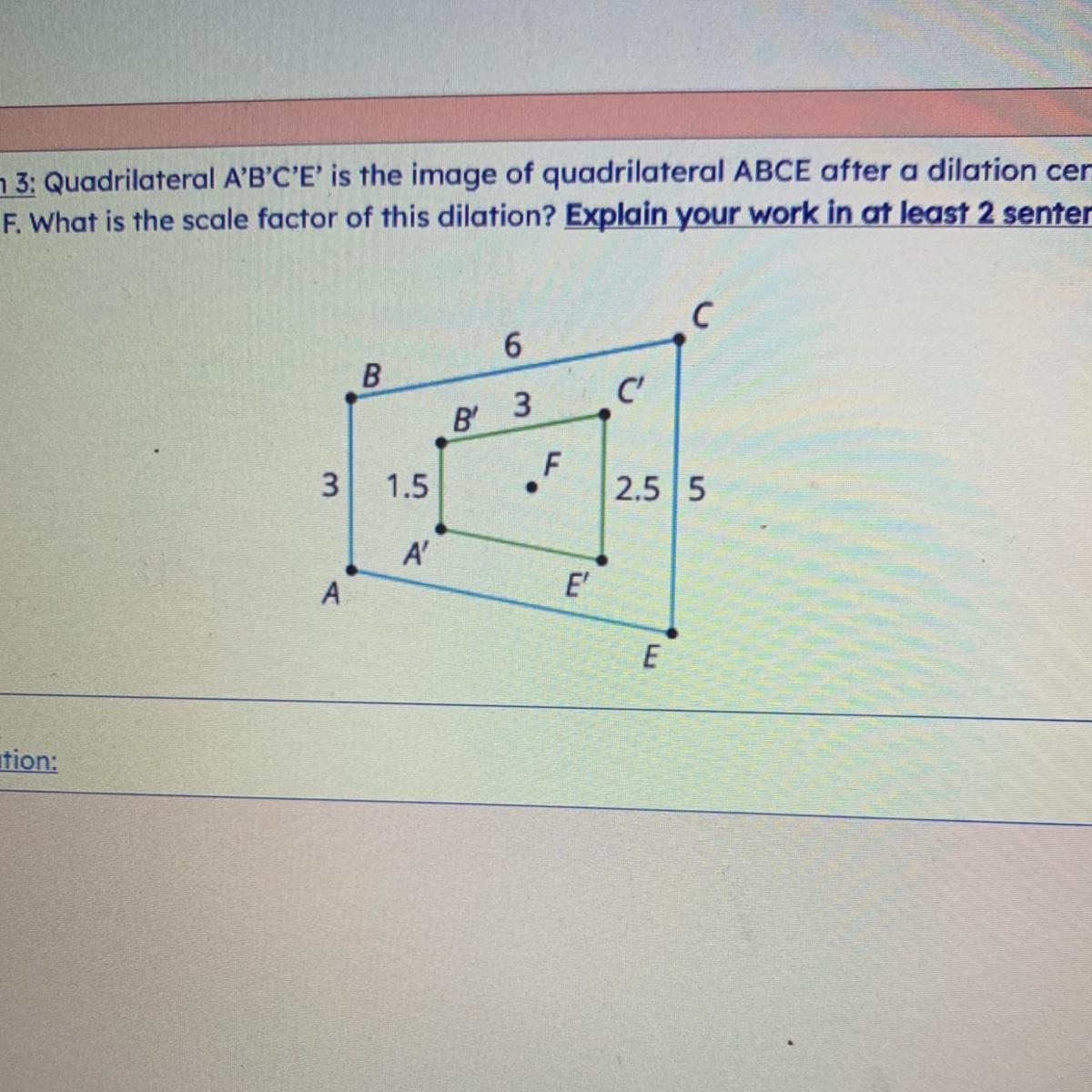
Question 3: Quadrilateral A'B'C'E' is the image of quadrilateral ABCE after a dilation centered
at point F. What is the scale factor of this dilation? Explain your work in at least 2 sentences.
C
6
B
C'
B 3
3
1.5
2.5 5
A
E
А
E
Answers
==========================================================
Explanation:
We have AB = 3 and A'B' = 1.5; the ratio between the two segment lengths is (A'B')/(AB) = (1.5)/(3) = 1/2 = 0.5
Similarly,
(B'C')/(BC) = (3)/(6) = 1/2 = 0.5(C'E')/(CE) = (2.5)/(5) = 1/2 = 0.5You only need to pick one of these statements to be able to find the scale factor. The scale factor of 1/2 or 0.5 indicates that the image is half as small compared to the preimage. More specifically, each segment of the image is half as small compared to the corresponding segment on the preimage.
A'B' is half as small as ABB'C' is half as small as BCC'E' is half as small as CEA'E' is half as small as AEWe don't have numbers for AE and A'E', but the last statement above must be true because the dilation applies to all segment lengths.
The scale factor of this dilation in the given quadrilateral will be equal to 0.5 times.
What is a Polygon?A polygon is described in geometry as a compact, two-dimensional shape having three or more straight lines. Poly, which means "many," and gon, which means "angle," make up the Greek word "Polygon." Polygons of several kinds can be seen all around us.
As per the given information in the question,
AB = 3 and A'B' = 1.5;
Then, a ratio of the two segment lengths exists.,
(A'B')/(AB) = (1.5)/(3) = 1/2
(A'B')/(AB) = 0.5
In the similar way,
(B'C')/(BC) = (3)/(6) = 1/2
(B'C')/(BC) = 0.5
(C'E')/(CE) = (2.5)/(5) = 1/2
(C'E')/(CE) = 0.5
A'B' is half as small as AB, B'C' is half as small as BC, C'E' is half as small as CE, A'E' is half as small as AE.
To know more about Polygon:
https://brainly.com/question/24464711
#SPJ5
what is a ratio of two measurements with different units
Answers
A ratio is a mathematical relationship that compares two quantities. When the two quantities have different units, the resulting ratio is called a dimensionless or unitless ratio.
When the two quantities have different units, the units cancel out, leaving only the numerical relationship between the two measurements.
Here's an example to illustrate this concept:
Let's consider the ratio of distance to time.
Suppose you have traveled a distance of 100 meters in 10 seconds.
The ratio of distance to time can be calculated as:
Ratio = Distance / Time = 100 meters / 10 seconds = 10 meters per second
In this case, the units of meters and seconds cancel out, and we are left with a ratio of 10, which is dimensionless or unitless.
The ratio represents the speed or rate of travel, indicating that you are covering 10 meters per second.
Similarly, any ratio involving two measurements with different units can be treated as a dimensionless quantity.
Examples of such ratios include:
- Price per unit: For instance, the ratio of cost to quantity, such as dollars per pound or euros per liter.
- Concentration: The ratio of the amount of solute to the volume or mass of the solvent, such as grams per liter or moles per kilogram.
- Efficiency: The ratio of useful output to input, such as miles per gallon or kilowatt-hours per ton.
In each of these cases, the units in the ratio cancel out, and what remains is a dimensionless quantity that represents the relationship between the two measurements.
To know more about this unitless ratio refer here:
https://brainly.com/question/30073651#
#SPJ11
A fair-sided coin is tossed 18 times.
Which of the experimental outcomes is most consistent with theoretical outcomes?
A. 4 heads and 14 tails
B. 6 heads and 12 tails
C. 9 heads and 9 tails
D. 10 heads and 8 tails
Answers
Quadrilateral OPQR is inscribed in circle N, as shown below. What is the measure of ∠QRO? (5 points)
Quadrilateral OPQR is inscribed in circle N. Angle O is labeled x plus 17 degrees, angle Q is 6x minus 5 degrees, and angle R i
41
67
113
139

Answers
Opposite angles of a cyclic quadrilateral are supplementary, so
\(x+17+6x-5=180 \\ \\ 7x+12=180 \\ \\ 7x=168 \\ \\ x=24 \\ \\ \\ \implies \angle QRO=2(24)+19=\boxed{67^{\circ}}\)
If $g(x) = 3x + 7$ and $f(x) = 5x - 9$, what is the value of $f(g(8))$?
Answers
Which expression is equivalent to 4/9 (2n - 3)? Please explain
Answers
Answer:
n=3/2
Step-by-step explanation:
4/9 (2n - 3)
8/9n-4/3=0
8/9n=4/3 (multipluy by 9)
8n=12
n=12/8 which simplifies to 3/2
Please Help!
{64,60,57,63,61,64,50,62,60,56,53,62,54,60,64,53,61,58,60,64,57,56,64,61,63}
According to Chebyshev's theorem, at least 88.9% of the data falls between approximately 47.62 and Blank
. (Round to the nearest hundredth.)
Answers
Answer: 100
Step-by-step explanation:
Because 88.9% of the data falls between approximately 47.62 and Blank.
4. Find the value of x.
6x + 14
8x + 12
Answers
The answer is x = 1, assuming that the space is meant to be an equal sign.
Find the length of the midsegment of the trapezoid.
M
MN
18
10

Answers
The length of the midsegment of the trapezoid is 14 units
How to find the length of the midsegment of the trapezoid?The midsegment of a trapezoid is the segment connecting the midpoints of the two non-parallel sides.
The length of the midsegment of a trapezoid is half of the sum of the lengths of the two parallel sides. Thus:
The length of the midsegment MN = (18+10)/2 = 28/2 = 14 units
Learn more about length of the midsegment of a trapezoid on:
https://brainly.com/question/7593624
#SPJ1
what is 1 half of 2 thirds
Answers
Explanation: first you multiply 1/2 and 2/3 which is 1.2/2.3 which =2/6 =1.2/3.2=1/3
7) What does a multiplier of \( 1.2 \) mean?
Answers
A multiplier of 1.2 means the value is multiplied or increased by a factor of 1.2.
A multiplier is a term used to represent a factor by which a value is multiplied or increased. It is a numeric value that indicates the extent of the increase or expansion of a given quantity. Multiplication by a multiplier results in scaling or changing the magnitude of the original value.
A multiplier of 1.2 indicates that a value will be increased by 20% or multiplied by a factor of 1.2. This means that when the multiplier is applied to the original value, the resulting value will be 1.2 times the original.
Read more about multipliers:
brainly.com/question/15883095
Maximize Q = xy, where x and y are positive numbers such that x + 3y2 = 25. The maximum value of Q is __ and occurs at x = __ and y = __
(Type exact answers in simplified form.)
Answers
The maximum value of Q is (75/6)(sqrt(25/6)) and occurs at x = 75/6 and y = sqrt(25/6).
Maximize Q = xy?
To maximize Q = xy with the constraint x + 3y² = 25, where x and y are positive values.
Solve the constraint equation for either x or y. Let's solve for x:
x = 25 - 3y²
Substitute this expression for x in the Q equation:
Q = (25 - 3y²)y
Take the derivative of Q with respect to y (dQ/dy):
dQ/dy = 25 - 6y²
Set the derivative equal to 0 and solve for y:
0 = 25 - 6y²
6y² = 25
y² = 25/6
y = sqrt(25/6)
Substitute this value of y back into the x equation:
x = 25 - 3(sqrt(25/6))²
x = 25 - 3(25/6)
x = 25 - 75/6
x = (25*6 - 75)/6
x = 75/6
Calculate the maximum value of Q using these x and y values:
Q = xy
Q = (75/6)(sqrt(25/6))
Thus, the maximum value of Q is (75/6)(sqrt(25/6)) and occurs at x = 75/6 and y = sqrt(25/6).
Learn more about derivative.
brainly.com/question/25324584
#SPJ11
A 40 cm spring will stretch one-sixth of the weight (in pounds) attached to it. Write a function to represent the situation.
Answers
From the problem, we know that the spring will stretch one-sixth of the weight attached to it. So:
S = (1/6)W + 40
This equation represents the situation where the length of the spring (S) is a function of the weight attached to it (W).
A supercomputer system has 50 jobs in the queue that will be executed in sequence. The times required to execute the jobs are independent and follow a common distribution that has mean 20 seconds and standard deviation 4 seconds. Approximate the probability that the supercomputer system will complete executing at least 25 of the jobs in the first 450 seconds.[Use the Central Limit Theorem]
Answers
The probability that the supercomputer system will complete executing at least 25 of the jobs in the first 450 seconds is approximately 0.9599, using the Central Limit Theorem.
Let X be the total time required to execute all the 50 jobs. Then, X follows a normal distribution with mean μ = 50 × 20 = 1000 seconds and standard deviation σ = 50 × 4 = 200 seconds, since the times required for each job are independent and identically distributed.
Now, let Y be the total time required to execute the first 25 jobs. Then, Y also follows a normal distribution with mean μ_Y = 25 × 20 = 500 seconds and standard deviation σ_Y = sqrt(25) × 4 = 20 seconds, since the times required for each job are independent and identically distributed.
To approximate the probability that the supercomputer system will complete executing at least 25 of the jobs in the first 450 seconds, we need to standardize the random variable (Y - μ_Y) / σ_Y and use the standard normal distribution.
P(Y >= 450) = P((Y - μ_Y) / σ_Y >= (450 - 500) / 20) = P(Z >= -2) = 0.9772
Therefore, the probability that the supercomputer system will complete executing at least 25 of the jobs in the first 450 seconds is approximately 0.9599, which is the complement of 0.9772.
For more questions like Probability visit the link below:
https://brainly.com/question/15198684
#SPJ11
When it was raining, Elliott drove for 120 miles. When the rain stopped, he drove
20 mph faster than he did while it was raining. He drove for 300 miles after the
rain stopped. If Elliott drove for a total of 10 hours, how fast did he drive while it
was raining?
Answers
Answer:
\(\boxed{22}.\)
Step-by-step explanation:
Since Elliott drove for a total of 10 hours, and he drove for 120 miles while it was raining and 300 miles after the rain stopped, we know that he drove for a total of 120 + 300 = <<120+300=420>>420 miles.
If he drove for a total of 10 hours and covered a distance of 420 miles, then his average speed was 420 miles / 10 hours = <<420/10=42>>42 mph.
Since Elliott drove 20 mph faster after the rain stopped than he did while it was raining, then we know that his speed while it was raining was 20 mph slower than his average speed of 42 mph. That means his speed while it was raining was 42 mph - 20 mph = <<42-20=22>>22 mph.
Calculate the zeros of the function f(x) = x2 – 12x + 35 by completing the square.
Answers
Answer:
x = 5, x = 7
Step-by-step explanation:
to find the zeros let f(x) = 0 , that is
x² - 12x + 35 = 0 ( subtract 35 from both sides )
x² - 12x = - 35
To complete the square
add ( half the coefficient of the x- term )² to both sides
x² + 2(- 6)x + 36 = - 35 + 36
(x - 6)² = 1 ( take the square root of both sides )
x - 6 = ± \(\sqrt{1}\) = ± 1 ( add 6 to both sides )
x = 6 ± 1
then
x = 6 - 1 = 5
x = 6 + 1 = 7
if f(x)= 3x + 10x and g(x)=5x - 3 find (f+g)(x)
Answers
Answer:
18x-3
Step-by-step explanation:
f(x)= 3x + 10x
g(x)=5x - 3
f(x)+g(x) = 3x + 10x + 5x - 3
Combine like terms
= 18x -3
Answer:
3^x+15x-3
Step-by-step explanation:
this is the right answer i just did it
\
Write the quotient and remainder when we divide (x^3 -4x^2 + 2x + 5) by (x - 2)

Answers
Answer:
Step-by-step explanation:
Sorry I can't explain how it is done. It is very difficult to explain on paper.

Please I need help!!! NO LINKS!!!!! Ill mark brainlest
The point ( − 2, 3) is the solution to which of the following equations?
A.y=x−1
B.y=3x−2
C.y=−x+1
D.y=−2x+3
Answers
Answer: C
Step-by-step explanation:
y=-x+1
3=-(-2)+1
3=2+1
Spencer is designing the interior of a house. The length of one room is twice as long as it's width
Answers
Need some help and fast

Answers
Answer:
highest 7/8, 0.5, -1/4, -1 1/5 lowest
Answer: i'm not certain but i think its -1 1/5 first then -1/4 next is 0.5 then 7/8
once again not certain but i think that's the answer
The start of the pyramid age began with King Zoser's pyramid, erected in the 27th century B.C. In its original state, it stood 62 meters
high with a rectangular base that measured
140 meters by 118 meters. Find the volume
of the original pyramid.
Answers
The problem requires finding the volume of the original pyramid built by King Zoser in the 27th century B.C. The pyramid had a rectangular base that measured 140 meters by 118 meters and a height of 62 meters.
To calculate the volume of the pyramid, we need to use the formula for the volume of a pyramid, which is given by 1/3 times the product of the base area and height.
Once we have calculated the volume, we will have a better understanding of the size and scale of the pyramid and the monumental effort required to construct it over 4000 years ago.
To find the volume of the pyramid, we need to first calculate the area of the rectangular base, which is given by multiplying the length and width. So, the area of the base is 140 x 118 = 16,520 square meters. Next, we can substitute the values of the base area and height into the formula for the volume of a pyramid to get the volume of the original pyramid. So, the volume is given by 1/3 x 16,520 x 62 = 343,200 cubic meters. Therefore, the original pyramid had a volume of 343,200 cubic meters, which gives us an idea of the immense size and grandeur of the ancient Egyptian pyramids.
To learn more about volume of the pyramid, click here:
brainly.com/question/17615619
#SPJ11
Please Help!!! Compare continuous functions f, g, and h, and match the statements with the function they best describe.
Drag each description to the correct location on the table.

Answers
Answer: Not sure if this is 100% correct, but it should be.
Step-by-step explanation:

A man saves $85.50 each month. Up to now he has saved $2137.50. How much were his total savings
15 months ago?
Answers
Answer:
$855.00
Step-by-step explanation:
85.50 x 15 = 1,282.50
2,137.50 - 1,282.50 = 855.00
Help please,
The height of a pizza box is 1 3/4 inches. What is the height in inches of 8 pizza boxes?
Answers
Answer:
14 inches
Step-by-step explanation:
1 3/4*8=
please help it almost due to 15 points
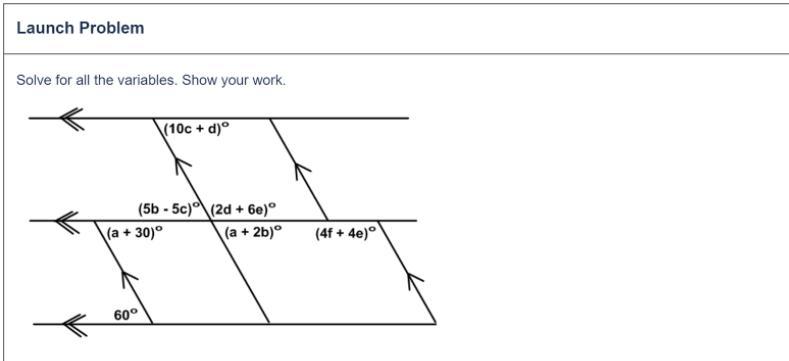
Answers
Answer:
a=30
b=15
c=3
d=30
e=10
Step-by-step explanation:
Solve for A first and continue solving for one variable at a time
A lottery offers one $1000 prize, one $400 prize, and 10 $100 prizes. One thousand tickets are sold at $2 each. Find the expectation (expected value) if a person buys one ticket.(The answer will be in dollars, but just type the amount, not the dollar sign. Be sure to indicate whether it is positive or negative.)
Answers
Total number of tickets is one thousand.
Formula for probability is given below as,
\(\text{Prob}=\frac{required\text{ outcome}}{total\text{ outcome}}\)Probability of one $1000 prize is given below as,
\(P(\text{\$1000)=}\frac{1}{1000}\)Probability of one $400 prize is given below as,
\(P(\text{\$400)=}\frac{1}{1000}\)Probability of ten $100 prize is given below as,
\(P(\text{\$100)=}\frac{10}{1000}=\frac{1}{100}\)For the expected value if each person buys one ticket,
\(\begin{gathered} Expected\text{ value=}(\frac{1}{1000}\times1000)+(\frac{1}{1000}\times1000)+(\frac{1}{100}\times1000) \\ \text{Expected value=}(1+1+10)=\text{\$12} \end{gathered}\)Expected value is $12
Use the distributive property to write an equivalent expression.
2(8x + 9)
Answers
Explanation:
When you distribute, 2x8=16 and you carry the x. Then, 2x9=18.
Hope this helps :)
I need help with this question

Answers
Answer:
Step-by-step explanation:

Find the median. 90, 88, 100, 82, 80.
Answers
Answer:
100 is the median for te above observations
HOPE IT HELPEDAnswer:
The median is 88.
Step-by-step explanation: