Choose the expression that represents a quadratic expression. 12x4 − 2x3 5x2 − 9x − 6 2x3 5x2 − 9x − 6 12x2 8x − 1 −8x − 1.
Answers
The correct expression that represents a quadratic expression is: 12x² + 8x - 1.
What is a quadratic equation?
A quadratic equation is an algebraic expression that involves numbers and variables choosing the second degree of x.
The common standard form of a quadratic equation takes the form: ax² + bx + cTherefore, we can conclude that the correct quadratic equation from the options is 12x² + 8x - 1.
Learn more about quadratic equation here:
https://brainly.com/question/1214333
Answer:
12x² + 8x - 1.
Step-by-step explanation:
Related Questions
If angle 1 = (2x+5) and angle 7 = (4x-17), find x
Answers
The value of x is 11
What is supplementary angle ?
Two angles are said to be supplementary if their sums total 180 degrees. A linear pair's two angles, like angles 1 and 2 in the illustration below, are always supplementary. But two angles don't have to be close to one another to be supplementary. In the following image, 3 and 4 are supplementary since their sums equal 180 degrees.
Angles ∠1 and ∠7 are alternate exterior angles where a transversal crosses parallel lines, so are congruent.
∠ 1 = ∠ 7
∴2x + 5 = 4x - 17
4x - 2x =17+5
2x = 22
x = \(\frac{22}{2}\)
x = 11
To learn more about supplementary angle from the given link
https://brainly.com/question/12881892
#SPJ1
Help please this is too hard for my brain
Answers
Answer:
the answer would be 1.5 cups of milk
Ellie is making a cake, The instructions say that the ratio of sugar to flour should be 1:3 Ellie uses 250g of sugar and 650g of flour: Has Ellie used the correct ratio of sugar to flour?
Answers
Answer:
No
Step-by-step explanation:
Ellie should be using 750(g) of flour instead of 650.
Answer:
No
Step-by-step explanation:
1 : 3
250: 750
She needs to add another 100 grams of flour.
What are the five key points that you need to find for any given set of numbers in order to draw a Box plot for the data. Write the answer. Help
Answers
The five-number summary is the minimum, first quartile, median, third quartile, and maximum. In a box plot, we draw a box from the first quartile to the third quartile.
Consider the following problem Maximize Z=90x
1
+70x
2
, subject to
2x
1
+x
2
≤2
x
1
−x
2
≥2
and x
1
≥0,x
2
≥0
Use the Big M method, work through the simplex method step by step to demonstrate that the problem has no feasible solutions. 4. Use the Big M method, work through the simplex method step by step to solve the following problem. Minimize Z=3x
1
+2x
2
+7x
3
, subject to
−x
1
+x
2
=10
2x
1
−x
2
+x
3
≥10
and x
1
≥0,x
2
≥0,x
3
≥0.
Answers
For the first problem, there are no feasible solutions. In the second problem, the optimal solution is x₁ = 0, x₂ = 0, x₃ = -10, with the minimum value of Z = -30.
To demonstrate that the first problem has no feasible solutions using the Big M method and the simplex method, we will first convert the problem into standard form. The standard form of a linear programming problem involves converting all inequalities into equations and introducing slack, surplus, and artificial variables as needed.
1. Convert the inequalities to equations:
2x₁ + x₂ + s₁ = 2 (Constraint 1)
X₁ - x₂ - s₂ = 2 (Constraint 2)
X₁, x₂, s₁, s₂ ≥ 0
2. Introduce artificial variables and a big M:
Z = 90x₁ + 70x₂ - M(a₁ + a₂) (Objective function)
2x₁ + x₂ + s₁ + a₁ = 2 (Constraint 1)
X₁ - x₂ - s₂ + a₂ = 2 (Constraint 2)
X₁, x₂, s₁, s₂, a₁, a₂ ≥ 0
3. Set up the initial simplex tableau:
| 2x₁ | x₂ | s₁ | s₂ | a₁ | a₂ | RHS |
Z | -90 | -70 | 0 | 0 | M | M | 0 |
S₁ | 2 | 1 | 1 | 0 | 1 | 0 | 2 |
S₂ | 1 | -1 | 0 | -1 | 0 | 1 | 2 |
4. Identify the pivot column (entering variable):
The most negative coefficient in the Z row is -90, so x₁ will enter the basis.
5. Identify the pivot row (leaving variable):
To determine the pivot row, calculate the ratio of the RHS to the positive coefficients in the entering column. Choose the smallest nonnegative ratio.
Ratios:
S₁: 2/2 = 1
S₂: 2/1 = 2
The smallest ratio is 1, so the pivot row is s₁.
6. Perform the pivot operation:
Divide the pivot row by the pivot element (1) to make the pivot element equal to 1:
| x₁ | x₂ | s₁ | s₂ | a₁ | a₂ | RHS |
Z | -90 | -70 | 0 | 0 | M | M | 0 |
X₁ | 1 | 0.5 |0.5 | 0 |0.5 | 0 | 1 |
S₂ | 1 | -1 | 0 | -1 | 0 | 1 | 2 |
Perform row operations to make all other entries in the pivot column equal to zero:
| x₁ | x₂ | s₁ | s₂ | a₁ | a₂ | RHS |
Z | 0 | 15 | -90 | 0 | -45 | 90 | -90 |
X₁ | 1 | 0 | 1 | 0 | 1 | 0 |
2 |
S₂ | 0 | -2 | -1 | -1 | -0.5| 1 | 0 |
7. Check for optimality:
Since there are negative coefficients in the Z row, the current solution is not optimal. We need to continue iterating.
8. Repeat steps 4-7 until an optimal solution is reached:
The next pivot column is x₂ (coefficient: 15).
The next pivot row is s₂ (ratio: 0/(-2) = 0).
Perform the pivot operation:
| x₁ | x₂ | s₁ | s₂ | a₁ | a₂ | RHS |
Z | 0 | 0 | -90 | 15 | -75 | 75 | -180|
X₁ | 1 | 0 | 1 | -0.5| 0.5 | -0.5| 1 |
X₂ | 0 | 1 | 0 | -0.5| -0.5| 0.5| 0 |
The coefficients in the Z row are now nonnegative, but the artificial variables (a₁ and a₂) remain in the basis. This indicates that the original problem is infeasible since the optimal value of the objective function is negative.
Therefore, the first problem has no feasible solutions.
Now, let’s solve the second problem using the Big M method and the simplex method.
1. Convert the inequalities to equations:
-x₁ + x₂ + s₁ = 10 (Constraint 1)
2x₁ - x₂ + x₃ + s₂ = 10 (Constraint 2)
X₁, x₂, x₃, s₁, s₂ ≥ 0
2. Introduce artificial variables and a big M:
Z = 3x₁ + 2x₂ + 7x₃ + M(a₁ + a₂) (Objective function)
-x₁ + x₂ + s₁ + a₁ = 10 (Constraint 1)
2x₁ - x₂ + x₃ + s₂ + a₂ = 10 (Constraint 2)
X₁, x₂, x₃, s₁, s₂, a₁, a₂ ≥ 0
3. Set up the initial simplex tableau:
| -x₁ | x₂ | x₃ | s₁ | s₂ | a₁ | a₂ | RHS |
Z | -3 | -2 | -7 | 0 | 0 | M | M | 0 |
S₁ | -1 | 1 | 0 | 1 | 0 | 1 | 0 | 10 |
S₂ | 2 | -1 | 1 | 0 | 1 | 0 | 1 | 10 |
4. Identify the pivot column (entering variable):
The most negative coefficient in the Z row is -7, so x₃ will enter the basis.
5. Identify the pivot row (leaving variable):
Calculate the ratio of the RHS to the positive coefficients in the entering column. Choose the smallest nonnegative ratio.
Ratios:
S₁: 10
/1 = 10
S₂: 10/1 = 10
Both ratios are the same, so we can choose either. Let’s choose s₁ as the pivot row.
6. Perform the pivot operation:
Divide the pivot row by the pivot element (1) to make the pivot element equal to 1:
| -x₁ | x₂ | x₃ | s₁ | s₂ | a₁ | a₂ | RHS |
Z | -3 | -2 | -7 | 0 | 0 | M | M | 0 |
S₁ | -1 | 1 | 0 | 1 | 0 | 1 | 0 | 10 |
S₂ | 2 | -1 | 1 | 0 | 1 | 0 | 1 | 10 |
Perform row operations to make all other entries in the pivot column equal to zero:
| -x₁ | x₂ | x₃ | s₁ | s₂ | a₁ | a₂ | RHS |
Z | 0 | 3 | -7 | 3 | 0 | -3 | 0 | -30 |
X₃ | 1 | -1 | 0 | -1 | 0 | -1 | 0 | -10 |
S₂ | 0 | -3 | 1 | 2 | 1 | 2 | 1 | 30 |
7. Check for optimality:
Since there are no negative coefficients in the Z row, the current solution is optimal.
9. Read the solution:
The optimal solution is:
X₁ = 0
X₂ = 0
X₃ = -10
S₁ = 10
S₂ = 30
A₁ = 0
A₂ = 0
The minimum value of Z is -30.
Therefore, the second problem is feasible and has an optimal solution with x₁ = 0, x₂ = 0, x₃ = -10, and Z = -30.
Learn more about Big M method here: brainly.com/question/31433274
#SPJ11
A sequence in which the ratio between the subsequent terms is the same is called a geometric progression.
The general term of a G.P. is: a =arn-1 The sum of the infinite terms of a G.P. is:
Answers
The sum of the infinite terms of a G.P. is (aᵣ / (1 - r))
A geometric progression (G.P.) is a sequence where each term is obtained by multiplying the preceding term by a constant ratio. The general term of a G.P. is given by the formula aₙ = aᵣ(r)^(n-1), where aᵣ is the first term and r is the common ratio.
The sum of infinite terms of a G.P. can be calculated using the formula Sₙ = a(1 - rⁿ) / (1 - r), where Sₙ is the sum of the first n terms of the G.P., a is the first term, and r is the common ratio.
As n approaches infinity, rⁿ approaches zero if the value of r is less than one. Hence, we can write the formula for the sum of infinite terms of a G.P. as S = a / (1 - r), provided that the value of r is less than one.
Therefore, the main answer can be written as the sum of the infinite terms of a G.P. is (aᵣ / (1 - r)), where aᵣ is the first term, and r is the common ratio.
For more questions like Geometric click the link below:
https://brainly.com/question/13008517
#SPJ11
select all options which are geometric sequences
Answers
The geometric sequences in the options are:
1, 5, 25, 125, 625...
2, 4, 8, 16, 32...
1, -1, 1, -1, 1...
How to find the geometric sequences in the options?Geometric sequence is a type of sequence in which the ratio of every two successive terms is a constant.
This ratio is also called the common ratio of the geometric sequence. In other words, in a geometric sequence, every term is multiplied by a constant which results in its next term.
Let's check if the common ratios are constant (the same):
Sequence 1:
Common ratio; 65/64 ≠ 66/65 [No]
Sequence 2:
Common ratio: 5/1 = 25/5 (i.e. 5) [Yes]
Sequence 3:
Common ratio: 4/2 = 8/4 (i.e. 2) [Yes]
Sequence 4:
Common ratio: 3/2 ≠ 5/3 [No]
Sequence 5:
Common ratio: -1/1 = 1/(-1) (i.e. -1) [Yes]
Sequence 6:
Common ratio: 8/14 ≠ 2/8 [No]
Sequence 7:
Common ratio: 1/1 ≠ 2/1 [No]
Sequence 8:
Common ratio: 8/5 ≠ 11/8 [No]
Learn more about geometric sequences on:
https://brainly.com/question/30239116
#SPJ1
let $p$ and $q$ be the two distinct solutions to the equation$$\frac{4x-12}{x^2 2x-15}=x 2.$$if $p > q$, what is the value of $p - q$?
Answers
let $p$ and $q$ be the two distinct solutions to the equation$$\frac{4x-12}{x^2 2x-15}=x 2.$$if $p > q$. The value of $p - q$ is 4.
To find the value of $p - q$, we first need to solve the given equation and determine the values of $p$ and $q$.
The equation is:
$$\frac{4x-12}{x^2 - 2x - 15} = x^2.$$
Step 1: Factorize the denominator:
The denominator can be factored as $(x - 5)(x + 3)$.
Step 2: Simplify the equation:
$$\frac{4x-12}{(x - 5)(x + 3)} = x^2.$$
Step 3: Multiply both sides of the equation by $(x - 5)(x + 3)$ to eliminate the denominator:
$$(4x - 12) = x^2(x - 5)(x + 3).$$
Step 4: Expand and rearrange the equation:
$$4x - 12 = x^4 - 2x^3 - 15x^2 + 25x.$$
Step 5: Rearrange the equation and combine like terms:
$$x^4 - 2x^3 - 15x^2 + 21x - 12 = 0.$$
Step 6: Factorize the equation:
$$(x - 3)(x + 1)(x - 2)(x + 2) = 0.$$
From this, we get four possible solutions: $x = 3$, $x = -1$, $x = 2$, and $x = -2$.
However, we are interested in the two distinct solutions $p$ and $q$, where $p > q$. Therefore, the values of $p$ and $q$ are $p = 3$ and $q = -1$.
Finally, we can find the value of $p - q$:
$$p - q = 3 - (-1) = 3 + 1 = 4.$$
Hence, the value of $p - q$ is 4.
Learn more about the denominator:
https://brainly.com/question/1217611
#SPJ11
Rewrite each of the following expressions without using absolute value.
a) |a| if a>0
b) |2b| if b<0
c) |c| if c <0
d) |3c| if c≥0
Answers
Answer:
a) answer is "a"
b) answer is "-2b"
c) answer is "-c"
d) answer is "3c"
Step-by-step explanation:
Absolute value is positive value of something.
a>0 then a must be positive so absolute value means nothing if a is already positive. Therefore answer is a.
b<0, so b must be negative. absolute value makes 2b positive but you know b is negative so answer is -2b.
c<0 same as a except sign is flipped so answer is negative instead of positive.
c>=0, C is either 0 or positive so absolute value does nothing yet again so answer is just 3c.
Sorry is explanation wasn't through i'm only in middle school
a. | a | > 0, a is greater than and less than zero.
b. | 2b | if b < 0, b is not less than zero not greater than zero.
c. | c | if c < 0, c is not less than zero not greater than zero.
d. | 3c | if c ≥ 0, c is greater than zero and less than zero.
What is an absolute value function?We know the absolute value function of the modulus function always outputs a positive value irrespective of the sign of the input.
In piecewise terms | x | = x for x ≥ 0 and | x | = - x for x < 0.
Given,
| a | > 0
∴ a is greater than and less than zero.
| 2b | if b < 0
b is not less than zero not greater than zero.
| c | if c < 0
c is not less than zero not greater than zero.
| 3c | if c ≥ 0.
c is greater than zero and less than zero.
learn more about modulus functions here :
https://brainly.com/question/13103168
#SPJ2
Please help me with this question so I can better help my son to understand this better. I have attached the graph that were working from below? The graph shows f(x)and its transformation g(x).Enter the equation for g(x) in the box.g(x) =
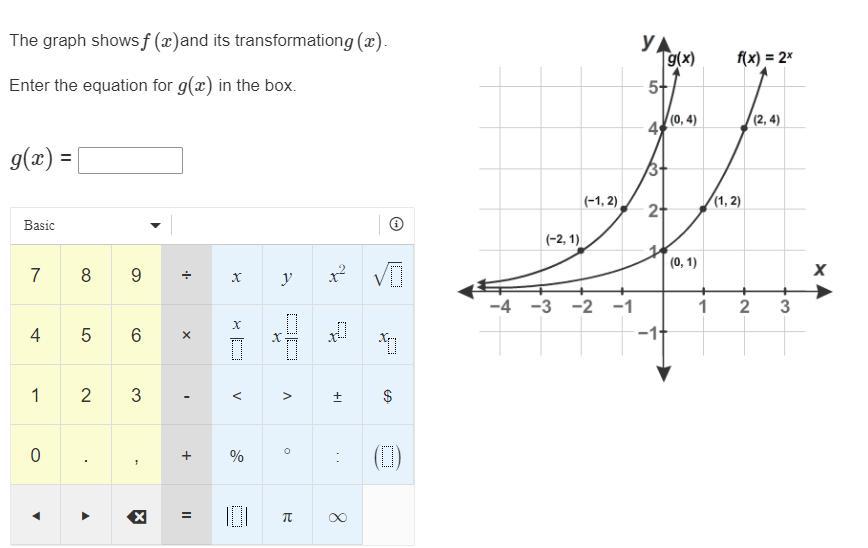
Answers
Answer
g(x) = 2ˣ⁺² or 2^(x + 2)
\(g(x)=2^{x+2}\)
Explanation
When a function f(x) is translated horizontally along the x-axis by a units, the new function is represented as
f(x + a) when the translation is by a units to the left.
f(x - a) when the translation is by a units to the right.
Looking at the coordinates of the points given on f(x) and g(x), we can see that g(x) is just f(x) translate 2 units to the left.
Hence, if f(x) = 2ˣ
g(x) = f(x + 2) = 2ˣ⁺² or 2^(x + 2)
Hope this Helps!!!
Can someone pls help me with this i need a answer and i need to explain pls help!i need to summit this in a few minss
Answers
Answer:
Your answer is d because 60+30*2 is 120 and 30 of 120 is 25%.
Step-by-step explanation:
Duo makes 65 percent of his dumplings with vegetarian fillings.
What fraction of Duo's dumplings have vegetarian fillings?
Answers
The fraction 13/20 of Duo's dumplings have vegetarian fillings.
What is fraction?
A fraction having whole numbers for the numerator and denominator. A fraction is a number of the form: ab where a and b are integers and b≠0. It represents the division of two numbers.
Given:
Duo makes 65 percent of his dumplings with vegetarian fillings.
According to given question we have
A percentage is a number or ratio expressed as a fraction of 100.
65 percent
=65 %
=65/100
Simplify fraction into simpler fraction,
⇒13/20
Therefore, the fraction 13/20 of Duo's dumplings have vegetarian fillings.
Learn more details about fraction here:
https://brainly.com/question/10354322
#SPJ1
35 X 6.7
What is this answer
Answers
Answer:
234.5
Step-by-step explanation:
Answer:
234.5
Step-by-step explanation:
Can someone help me with this question? If I can get an equation for it and an explanation of how to do it then I should be able to do the rest of them.
The problem wants me to:
"write the equation of the parabola in intercept form."
Answers
2. Janet rolls a regular eight-sided die with numbers 1 to 8. Find the
probability that she gets a 5.
Answers
Answer:
Step-by-step explanation:
Adult tickets to the fall play cost $8 and student tickets cost $4. The drama class sold 30 more adult tickets than student tickets to the fall play. If the class collected 840 from ticket sales, how many adult tickets were sold?
Answers
The number of adult tickets that were sold would be = 435 tickets.
What is a ticket?A ticket is an official document that gives an individual access to an event.
The cost of adult tickets = $8
The cost for student tickets = $4
The number of students tickets sold = X
The number of adults tickets sold = X +30
The told number of tickets sold = 840
To find X;
X + X + 30 = 840
2x + 30 = 840
2x = 840-30
2x = 810
X = 810/2
X = 405
Therefore, the number of tickets sold for adults = 405 +30 = 435 tickets.
Learn more about tickets here:
https://brainly.com/question/25333829
#SPJ1
Last week, Mel ate 3 apples, 2 bananas, and 4 oranges. Find the ratio of bananas to the total of fruit.
Answers
Answer:
2:9
Step-by-step explanation:
there are 2 bananas.
the total amount of fruit is 9 because 2+4+3= 9.
the ratio is 2:9 because there are 2 bananas and 9 fruits in total.
2:9 cannot be simplified any smaller.
Answer:
2:9
Step-by-step explanation:
3 apples, 2 bananas and 4 oranges
bananas: total number of fruits
3 : 3 + 2 + 4
2:9
What is the percent of 40 of 230
Answers
Answer:
17.39
Step-by-step explanation:
40:230*100 =
( 40*100):230 =
4000:230 = 17.39
Answer:
20 % would be ur answer to ur question
Last year, Erin earned $1,497.75. This year, she earned 2.9 times as much as
last year. Which of the following answer choices is the most reasonable
estimate for the amount of money Erin earned this year?*
Answers
Answer:
4,343.475
Step-by-step explanation:
I just multiplied what she earned and how much she is going to make
Can a linear function be an exponential function?
Answers
A linear growth function has a positive constant slope, whereas an exponential growth function has a positive rising slope.
Is it possible for a linear equation to be exponential?Explanation and response: Exponents are not permitted in a linear equation. Because the link between the two variables does not vary at a constant pace, the exponents in an equation generate a nonlinear graph. Linear functions have a constant rate of change per unit interval. Over equal intervals, an exponential function changes by a similar ratio.
The exponential function is another sort of nonlinear function.A nonlinear function in which the independent variable equals the function’s exponent, as in… The independent variable in these functions is an exponent in the equation. Exponential functions are shown as straight lines on semilog paper. Semi-log paper contains two axes: one arithmetic and one logarithmic. The exponential constant in the equation is given by the slope of the line (m).
To learn more about linear equation to refer:
https://brainly.com/question/29051317
#SPJ4
Find the slope of the line that passes through (10, 3) and (1, 10).
Simplify your answer and write it as a proper fraction, improper fraction, or integer.
Answers
Answer: -7/9
Step-by-step explanation:
10-3
1-10
The slope of the line is - 7/9
please see the attached picture for full solution
Hope it helps
Good luck on your assignment
Once chosen, a score, event, or participant CANNOT be returned to the population to be selected again. This technique is referred to as
a. random sampling without replacement.
b. random sampling with replacement.
c. stratified random sampling.
d. convenience sampling.
Answers
The technique being described is random sampling without replacement, which is option a.
This technique is called "sampling without replacement."
However, you've also mentioned convenience sampling, which is a different method.
Let me briefly explain both concepts.
Sampling without replacement is a method in which each item, score, event, or participant is chosen from the population and is not returned to the pool for further selections.
This ensures that each element can only be selected once, eliminating the chance of duplication in the sample.
This method is often used in surveys, experiments, and research to maintain the independence of observations and provide a more accurate representation of the population.
Select an item, score, event, or participant from the population.
Record the selected item and remove it from the population.
Repeat steps 1-2 until the desired sample size is obtained.
Convenience sampling, on the other hand, is a non-probability sampling method where researchers select participants based on their accessibility and ease of recruitment.
This approach may introduce bias and limit the generalizability of the study results, as it does not ensure that the sample is representative of the population.
Identify the target population.
Recruit participants who are easily accessible and willing to participate.
Collect data from the selected participants.
In summary, sampling without replacement is a technique that prevents the same item from being selected more than once, while convenience sampling is an approach that focuses on selecting participants based on their accessibility. Both methods serve different purposes in research and should be chosen based on the study's objectives and available resources.
Option a is correct.
For similar question on sampling.
https://brainly.com/question/14735856
#SPJ11
1. Calculate the area of the following parallelogram:
28 in²
26 in²
40 in²
30 in²
Answers
The area of the parallelogram is 30 square inch.
What is the area of the parallelogram?A parallelogram is simply a quadrilateral with two pairs of parallel sides.
The area of parallelogram is expressed as:
A = base × height
From the diagram:
base of the parallelogram = 10 inHeight of the parallelogram = 3 inArea = ?Plug the given values into the above equation and solve for area.
Area = base × height
Area = 10 in × 3 in
Area = 30 in²
Therefore, the area is 30 in².
Option D) 30 in² is the correct answer.
Learn more about parallelogram here: https://brainly.com/question/1563728
#SPJ1
I need help and for the other select it’s are or are not
Answers
Answer:
Step-by-step explanation:
It's clear from the graph that the angles of the given triangles are different.
And for similarity of two triangles, at least two angles of the triangles should be congruent.
Therefore, both the triangles are not similar.
The angles are DIFFERENT.Since similarity transformations preserve angle measures, ΔUVW and ΔGHI ARE NOT similar.
a group of teachers, parents, and students attended a concert. the adults paid $1,200 altogether and the students paid $640 altogether for their tickets. the price of an adult ticket was $60, and there were 4 more teachers than parents. how many parents were there in the group?
Answers
There were 4 parents in the group attending a concert.
The number of adults = total amount paid for the ticket ÷ cost of each ticket
The number of adults = 1200 ÷ 60
Performing division
The number of adults = 20
Let the number of parents be x. So, the number of teachers will be (20 - x). But, number of teachers is (x + 4). So, relating the two -
20 - x = x + 4
Rewriting the equation
x + x = 20 - 4
Performing addition on LHS and subtraction in RHS
2x = 16
Performing division
x = 8
There were 8 parents in the group.
Learn more about equations -
https://brainly.com/question/21405634
#SPJ4
T/F: An intercepted arc is twice the measure of the inscribed angle it was created from.
Answers
False. The intercepted arc is actually twice the measure of the inscribed angle only if the inscribed angle is an angle at the center. If the inscribed angle is not at the center, the intercepted arc will have a different measure.
So, in general, the relationship between the measure of the intercepted arc and the inscribed angle it was created from depends on the location of the inscribed angle in the circle. This is a long answer, but it provides a detailed explanation of the relationship between the intercepted arc and the inscribed angle in different scenarios.
AN intercepted arc is twice the measure of the inscribed angle it was created from.
In a circle, when an inscribed angle is formed by two chords, it intercepts an arc on the circle. According to the Inscribed Angle Theorem, the measure of the inscribed angle is half the measure of the intercepted arc. Therefore, the intercepted arc is indeed twice the measure of the inscribed angle.
To know more about inscribed angle visit:-
https://brainly.com/question/29028021
#SPJ11
1. You are building a porch that
has a perimeter of 28 ft. If the
width of the porch is four less
than the length find the length of
the porch?
Answers
Answer:
2
Step-by-step explanation:
because i don't know okay
Answer:
9 ft.
Step-by-step explanation:
1.
If there are 2 sides for width and 2 sides for length, you would need to add the difference from both the sides of length which would be 8.
2.
28 - 8 = 20.
So if all the sides were equal, each one would be 5 ft.
If the each length side is 4 more than the width sides, you would add 4 to 5 so each length side is 9. So the length of the porch is 9 ft.
$10,500 is shared between Peter and John in the ratio 7:3. Calculate the amount of money each person received.
Answers
Answer:
John=3150 peter=7350
Step-by-step explanation:
Hope this helps
Find the equation that intersects the x-axis at point (3, 0) and
intersects the y-axis at
point (0, 5). Then sketch the diagram.
Answers
The equation of the line that intersects the x-axis at point (3, 0) and intersects the y-axis at point (0, 5) is y = (-5/3)x + 5.
To find the equation of a line that intersects the x-axis at point (3, 0) and intersects the y-axis at point (0, 5), we can use the slope-intercept form of a linear equation, which is y = mx + b. Given the point (3, 0) on the x-axis, we know that when x = 3, y = 0. This gives us one point on the line, and we can use it to calculate the slope (m).
Using the slope formula: m = (y2 - y1) / (x2 - x1)
Substituting the values (0 - 5) / (3 - 0) = -5 / 3
So, the slope (m) is -5/3. Now, we can substitute the slope and one of the given points (0, 5) into the slope-intercept form (y = mx + b) to find the y-intercept (b).
Using the point (0, 5):
5 = (-5/3) * 0 + b
5 = b
The y-intercept (b) is 5. Therefore, the equation of the line that intersects the x-axis at point (3, 0) and intersects the y-axis at point (0, 5) is:
y = (-5/3)x + 5
To sketch the diagram, plot the points (3, 0) and (0, 5) on the x-y plane and draw a straight line passing through these two points. This line represents the graph of the equation y = (-5/3)x + 5.
To know more about equation,
https://brainly.com/question/28164076
#SPJ11
An animal shelter takes in an average of 5 animals per day. The shelter must keep its total occupancy below 300. Currently, the shelter has 165 animals. If none of the animals get adopted, which inequality represents how many more days, x, the shelter can continue to take in animals without exceeding its occupancy limit?
Answers
Answer:
5x less than 300 - 165
Step-by-step explanation:
It will take 27 days to take in animals without exceeding its occupy limit.
What is algebraic expression ?An expression which is made up of variables and constants , along with algebraic operation (addition , subtraction etc ) is called Algebraic expression.
According to the question :
165 + (x) 5 = 300
5x = 135
x = 27
Hence , it will take 27 days to occupy the limit
Learn more about algebraic expression :
https://brainly.com/question/953809?referrer=searchResults
#SPJ2