can someone please solve a graph to this and write in as an equation, thank you so much

Answers
The following expression represents a 2-scale factor vertical stretch, a transformation of 4 units left, and a transformation of 1 unit down:
g(x) = 2f(x + 4) - 1
How to write the given transformation?A vertical stretch of scale factor K is expressed as follows for the general function f(x):
g(x) = Kf(x).
Horizontal translation:
A horizontal translation of N units for a general function f(x) is written as:
g(x) = f(x + N).
The shift is to the left if N is positive and the shift is to the right if N is negative.
Vertical translation:
A vertical translation of N units for a generic function f(x) is expressed as follows:
g(x) = f(x) + N.
When N is positive, there is an upward movement and N shifts downward if it is negative.
So, if we start with a function f(x) and we stretch it vertically with a scale factor of 2, we get:
g(x) = 2f(x)
Then we translate it into 4 units left:
g(x) = 2f(x + 4)
Then we translate 1 unit down:
g(x) = 2f(x + 4) - 1
This is the equation for the transformation.
To learn more about transformations refer to:
brainly.com/question/4289712
#SPJ4
Related Questions
Can someone help me with this?

Answers
Answer:
6 units i think but i dont u how u do it
Tati made an impulse purchase by buying a $1000 handbag. An impulse purchase means that she most likely did not think of the____ alternatives for the $1000. a. best b. explicit c. implicit d. worst
Answers
An impulse purchase refers to a spontaneous buying decision made without much prior thought or consideration.
In the case of Tati buying a $1000 handbag, it implies that she most likely did not think of the explicit alternatives for that $1000.
When we talk about explicit alternatives, we are referring to the specific and consciously considered options that could be chosen instead of the purchase made. These alternatives are typically thought of and evaluated before making a decision.
In the context of Tati's impulse purchase, it suggests that she did not take the time to consider other specific options for how to spend the $1000. Instead, she made the decision to buy the handbag without consciously thinking about alternative uses for that money.
It's important to note that the other answer options, such as "best," "implicit," and "worst," are not accurate in this scenario.
The probability of impulse purchase is not related to determining the best or worst choice, nor does it involve implicit considerations. It specifically refers to the lack of considering explicit alternatives at the time of the purchase.
Learn more about probability here: brainly.com/question/31828911
#SPJ11
suppose that a is orthogonal to b in rn. what is projab? why? give a geometric interpretation in r2 or r3
Answers
Projab is the projection of vector a onto vector b. It is a vector that is perpendicular to b and has the same magnitude as a, and it is the vector that is closest to a in the direction of b.
In R2, the geometric interpretation is that projab is the vector that is obtained by dropping a perpendicular line from the tip of a onto the line containing b.
In R3, the geometric interpretation is that projab is the vector that is obtained by dropping a perpendicular line from the tip of a onto the plane containing b.
The equation for projab is projab = (a.b/|b|^2)b, where a.b is the dot product of a and b, and |b| is the magnitude of b.
The best estimator's error vector, when seen in terms of mean square errors, is orthogonal to all other feasible estimators, according to the orthogonality principle. The orthogonality principle can be expressed in a variety of ways, but it is most frequently used to describe linear estimators.
For more questions like orthogonal visit the link below:
https://brainly.com/question/28481384
#SPJ4
What is (−2) ( 3 4 /7 ) ?
Answers
Answer:-7 1/7 or -7.14285714286
Step-by-step explanation:
(−2) ( 3 4 /7 )
(-2)(25/7)
(-50/7)
-7 1/7
Or in decimals: -7.14285714286
HURRY PLZ I WILL GIVE BRAINLIEST....Fernando evaluated the expression below. StartFraction 5 (9 minus 5) over 2 EndFraction + (negative 2) (negative 5) + (negative 3) squared = StartFraction 5 (4) over 2 EndFraction minus 10 + 9 = StartFraction 20 over 2 EndFraction minus 10 + 9 = 10 minus 10 + 9 = 9. What was Fernando’s error? Fernando evaluated the numerator of the fraction incorrectly. Fernando simplified StartFraction 20 over 2 EndFraction incorrectly. Fernando incorrectly found the product of –2 and –5. Fernando evaluated (negative 3) squared incorrectly.
Answers
Answer:
The correct answer is...
Fernando incorrectly found the product of –2 and –5.
I hope this helps! Have a nice day!
A container built for transatlantic shipping is constructed in the shape of a right rectangular prism. Its dimensions are 7.5 ft by 7.5 ft by 6 ft. If the container is entirely full and, on average, its contents weigh 0.05 pounds per cubic foot, find the total weight of the contents. Round your answer to the nearest pound if necessary.
Answers
Answer:
Step-by-step explanation:
V = w h l
V = 7.5 * 7.5 * 6
V = 337.5cubic feet * 0.05
V = 16.875Lbs
V = 17Lbs (Rounded to nearest pound)
Type the integer that makes the following addition sentence true:
-5+? = -8
Answers
The answer to this question is -3
Answer:
The answer of -5+?=8
Let ? be x
so, A.T.Q
-5+x=8
we take x Right hand side and -5 left hand side with 8
x=8+5
x=13
so, the answer is -5+13=8
The depth of water in a reservoir increases from 14m to 15.75m. Work out the percentage increase.
Answers
Answer:
It was a 12.5% water gain
valencia theater sold 487 tickets for a play. tickets cost $14 per student with valid valencia identification and $25 per non-student. if total receipts were $8391, how many valencia student tickets and non-student tickets were sold?
Answers
354 Valencia student tickets and 133 non-student tickets were sold.
Let's use algebra to solve the problem. Let
x be the number of Valencia student tickets sold
y be the number of non-student tickets sold
We know that
x + y = 487 (the total number of tickets sold is 487)
14x + 25y = 8391 (the total receipts from ticket sales is $8391)
We can use the first equation to express one of the variables in terms of the other. For example, we can solve for y
y = 487 - x
Here we have to use the substitution method, we can then substitute this expression for y into the second equation
14x + 25(487 - x) = 8391
Simplifying and solving for x
14x + 12275 - 25x = 8391
-11x = -3884
x = 354
So, 354 Valencia student tickets were sold. We can use the first equation to find y
x + y = 487
354 + y = 487
y = 133
So, 133 non-student tickets were sold.
Learn more about substitution method here
brainly.com/question/30284922
#SPJ4
Determine if the following functions are even, odd, or neither. Show your work.
a. f(x)=x√1−x^2
b. g(x)=x^2−x
c. f(x)=1/5x^6−3x^2
Answers
To know more about the evenness or oddness of the given functions: the function f(x) = x√(1 - x²) is odd, the function g(x) = x² - x is neither even nor odd, and the function f(x) = (1/5)x⁶ - 3x² is even.
a. The function f(x) = x√(1 - x²) is an odd function.
To determine if a function is odd, we need to check if f(-x) = -f(x) for all x in the domain. Substituting -x into the function, we have f(-x) = (-x)√(1 - (-x)²) = -x√(1 - x²) = -f(x), which satisfies the condition for odd functions.
b. The function g(x) = x² - x is neither even nor odd.
To check for evenness, we need to verify if g(-x) = g(x) for all x in the domain. Substituting -x into the function, we have g(-x) = (-x)² - (-x) = x² + x, which is not equal to g(x) = x² - x. Therefore, g(x) is not even.
To check for oddness, we need to verify if g(-x) = -g(x) for all x in the domain. Substituting -x into the function, we have g(-x) = (-x)² - (-x) = x² + x, which is not equal to -g(x) = -(x² - x) = -x² + x. Therefore, g(x) is not odd.
c. The function f(x) = (1/5)x⁶ - 3x² is an even function.
To determine if a function is even, we need to check if f(-x) = f(x) for all x in the domain. Substituting -x into the function, we have f(-x) = (1/5)(-x)⁶ - 3(-x)² = (1/5)x⁶ - 3x² = f(x), which satisfies the condition for even functions.
To know more about even functions click here: brainly.com/question/23446734
#SPJ11
Need help ASAP please

Answers
Answer:
5 inches is 5 times as big as 1 inch.12.7 centimeters is 5 times as big as 2.54 centimeters.Step-by-step explanation:
5 ÷ 1 = 512.7 ÷ 2.54 = 5I hope this helps!
write the following expression as a function of an acute angle. cos (125°) -cos55° cos35° cos55°
Answers
The expression cos (125°) - cos 55° cos 35° cos 55° can be written as cos (55°) + cos (55°) cos (35°) cos (55°).
cos (125°) can be rewritten as cos (180° - 125°). Similarly, cos (35°) can be rewritten as cos (180° - 35°). Therefore, the expression can be written as:
cos (180° - 125°) - cos (55°) cos (180° - 35°) cos (55°)
Simplifying further, we have:
cos (55°) - cos (55°) cos (145°) cos (55°)
Since 145° is the supplement of 35°, we can rewrite it as:
cos (55°) - cos (55°) cos (180° - 35°) cos (55°)
Now, cos (180° - 35°) is equal to -cos (35°). Therefore, the expression becomes:
cos (55°) + cos (55°) cos (35°) cos (55°)
Hence, the expression as a function of an acute angle is:
cos (55°) + cos (55°) cos (35°) cos (55°)
To know more about expression,
https://brainly.com/question/29082858
#SPJ11
write (14+x)+(12x-8) in standard form
Answers
Answer:
13x+6
Step-by-step explanation:
really simple math question, pls help

Answers
Answer:
Quadrilateral
Step-by-step explanation:
No sides are parallel so it's not a trapezoid
someone help as soon as possible pls

Answers
Answer:
Check the explanation below please! :)
Step-by-step explanation:
"It is provided that the students has to select new colors for the hats and the pants of the marching band uniforms.
The color options for each item are: yellow (Y), green (G), or black (B).
The sample space for the color selection of hats and pants is:
Sample Space
Hats Pants
Y Y
Y G
Y B
G Y
G G
G B
B Y
B G
B B
There are a total of 9 possible selections."
Credit goes to: https://brainly.com/app/profile/13544493/answers
Find the area of each regular polygon below. Round values to the nearest 0.01. Show work for all steps clearly.

Answers
The area of the hexagon and pentagon area 779.4cm^2 and 84.303cm^2 respectively.
Data;
apothem = 15Area of a HexagonThe area of a hexagon with apothem 15 can be calculated by first finding the length of the side of the hexagon.
Length of hexagon can be found using trigonometric ratio;
\(a = x\sqrt{3}\)
Making x the subject of formula
\(x = \frac{a}{\sqrt{3} }\\x = \frac{15}{\sqrt{3} }\\x = 8.660\)
And then the length of the side is 2x
\(s = 2 * 8660 = 17.32\)
The perimeter of the hexagon is;
\(p = 6s \\p = 6 * 17.32=103.92\)
And the area is given as
\(A = \frac{1}{2} * perimeter * apothem\\A = \frac{1}{2} * 103.92 * 15\\A = 779.4unit^2\)
The area of the hexagon is 779.4 squared unit.
Area of the pentagonThe area of the pentagon can be found using several methods, but we can simply find the angle between the sides if we divide the pentagon into 10 pieces and then substitute the formula.
Total area of a pentagon is 360 degree.
\(\theta = \frac{360}{10} = 36^0\\\)
The area of a pentagon is given as
\(A = \frac{5s^2}{4 tan \theta} \\A = \frac{5 * 7^2}{4* tan36} \\A = 84.303cm^2\)
The area of the pentagon is 84.303cm^2
From the calculations above, the area of the hexagon and pentagon area 779.4cm^2 and 84.303cm^2 respectively
Learn more on area of polygons here;
https://brainly.com/question/1592439
a random sample of 2,000 members of a union reveals that 1,600 would vote yes on a merger proposal. what is the 95% confidence interval for the population proportion of members who would vote yes?
Answers
The 95% confidence interval for the population proportion of members who vote yes is (0.782, 0.818).
What is Random Sample?A choice that is made at random (purely by chance, with no predictability). They tapes of samples are:
Convenient: Sample taken from a pool that is easily accessible.
Random: Put all the possibilities into a hat, then pull some of them at random. Every kth element is taken in a systematic manner. If you wanted to survey anything on the street, for instance, you may interview every fifth person.
Cluster: The population is divided into groupings, or clusters, and every component of each cluster is surveyed.
Stratified: Additionally stratifies the people into several groupings. But only a small portion of the group is questioned after that.
Now, finding the sample proportion,
\(p=\frac{x}{n} \\\\=\frac{1600}{2000}\\\\ =0.8\)
The confidence level is given as,
\(C=p\pm[z(\frac{\alpha}{2})\times\sqrt{\frac{p(1-p)}{n} } ]\)
The value of \(z(\frac{\alpha}{2})\) is 1.96
Putting the values, we get
\(C=0.8\pm[1.96\times\sqrt{\frac{0.8(1-0.8)}{2000} } ]\\\\C=0.8\pm[1.96\times\sqrt{\frac{0.8(0.2)}{2000} } ]\\\\C=0.8\pm0.018\\\\C=(0.782,0.818)\)
Therefore, the 95% confidence interval is (0.782,0.818).
To learn more about the Random Samples visit here:
https://brainly.com/question/17831271
#SPJ4
The given question is incomplete. Here is the complete question.
a random sample of 2,000 members of a union reveals that 1,600 would vote yes on a merger proposal. what is the 95% confidence interval for the population proportion of members who would vote yes?
a) 0.782 to 0.818
b) 0.754 to 0.799
c) 0.690 to 0.713
d) 0.799 to 0.951
the product of 2 and d
Answers
Answer:
10
Step-by-step explanation:
if you multiply 2 and 5 together, you get a product of 10.
Answer: it would be 2d because its the product and product means to multiply
what is the value of x??
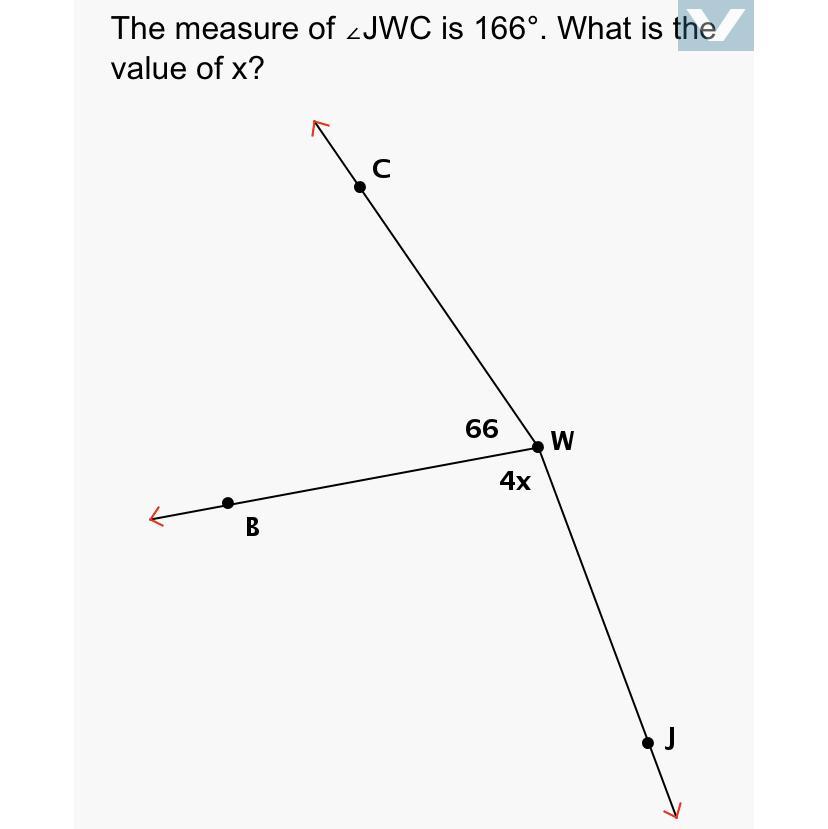
Answers
Answer:
\(\displaystyle 25 = x\)
Step-by-step explanation:
You are given the angle of the whole set, so set both expressions equivalent to the given angle measure:
\(\displaystyle 166° = 66° + [4x]° \hookrightarrow \frac{100}{4} = \frac{4x}{4} \\ \\ \boxed{25 = x}\)
I am joyous to assist you at any time.
Consider the function h defined by h(x)=−5x−3. Evaluate the following: a. h(4)= b. h(−6)= Find the following values of the function
f(−2)=
f(4)=
f(6)=
Solve this inequality: x+4>10 Please type: - inf for [infinity], - >= for ≥, - and ≪= for ≤ In set-builder notation, the solution set is An example of set-builder notation is {x∣x>1}. The I symbol is above the keyboard's Enter key. In interval notation, the solution set is An example of interval notation is (1,[infinity]).
Answers
For the function h defined by h(x) = −5x − 3a, a. h(4) = -23, b. h(-6) = 27. The solution of the given inequality x + 4 > 10 is (6, [infinity]) in interval notation.
For the function h defined by h(x) = −5x − 3a, we substitute the value of x to get the output value:
a. h(4) = -5(4) - 3 = -20 - 3 = -23
b. h(-6) = -5(-6) - 3 = 30 - 3 = 27
For the given function f, there is no explicit definition for f(x) provided. Therefore, the values of f(-2), f(4), and f(6) cannot be found.
To solve the given inequality x + 4 > 10, we subtract 4 from both sides of the inequality, and we have x > 6. The solution set can be expressed in set-builder notation as {x | x > 6} and in interval notation as (6, infinity). Therefore, the solution of the given inequality is (6, [infinity]) in interval notation.
To know more about function, refer here:
https://brainly.com/question/30721594
#SPJ11
00 which statement best describes the
solutions to the scenario above?
A) Potrick con eat out only 1 time per week.
B Potick can eat out e'ther 1 or 2 times per week.
© Patrick con eat out 1, 2 or 3 times per week.
D) Potrick con cot Out 1, 2, 3, or times per week.
a 20/20 The Marn Cafe

Answers
Answer: D) Potrick con cot Out 1, 2, 3, or times per week.
(hope this helps!)
1. Give the formula for the forward Fourier Transform for a signal, X(jω)=F{x(t)}. 2. Give the formula for the inverse Fourier Transform of a signal, x(t)=F−1{X(jω)}. Compare this to the formula from problem 1) above and discuss similarities and differences. What is the Fourier Transform property called which refers to the similarity between the two formulas? 3. Using the defining integral of the Fourier Transform, determine the transform of the following signal: x(t)=⎣⎡−1,1,0,−1
Answers
The forward Fourier Transform formula for a signal is X(jω) = F{x(t)}. The inverse Fourier Transform formula is x(t) = F^(-1){X(jω)}. The two formulas are related by the Fourier Transform property called duality or symmetry.
1. The forward Fourier Transform formula is given by:
X(jω) = ∫[x(t) * e^(-jωt)] dt
This formula calculates the complex spectrum X(jω) of a signal x(t) by integrating the product of the signal and a complex exponential function.
2. The inverse Fourier Transform formula is given by:
x(t) = (1/2π) ∫[X(jω) * e^(jωt)] dω
This formula reconstructs the original signal x(t) from its complex spectrum X(jω) by integrating the product of the spectrum and a complex exponential function.
The similarity between these two formulas is known as the Fourier Transform property of duality or symmetry. It states that the Fourier Transform pair (X(jω), x(t)) has a symmetric relationship in the frequency and time domains. The forward transform calculates the spectrum, while the inverse transform recovers the original signal. The duality property indicates that if the spectrum is known, the inverse transform can reconstruct the original signal, and vice versa.
3. To determine the Fourier Transform of the given signal x(t) = [-1, 1, 0, -1], we apply the defining integral:
X(jω) = ∫[-1 * e^(-jωt1) + 1 * e^(-jωt2) + 0 * e^(-jωt3) - 1 * e^(-jωt4)] dt
Here, t1, t2, t3, t4 represent the respective time instants for each element of the signal.
Substituting the time values and performing the integration, we can obtain the Fourier Transform of x(t).
Note: Please note that without specific values for t1, t2, t3, and t4, we cannot provide the numerical result of the Fourier Transform for the given signal. The final answer will depend on these time instants.
Learn more about Fourier here:
https://brainly.com/question/33191499
#SPJ11
Can someone help with this

Answers
Answer:
can you post the whole screen
Find the missing side:
Which is the right one

Answers
Answer:
D , drinking coffee
Step-by-step explanation:
hope this helps you somehow

If the concentration of the first tube is 150 ng/ml, what are the concentrations of the other three tubes?
Answers
The concentrations of the other three tubes are 1500 ng/ml, 15000 ng/ml, and 150000 ng/ml, respectively.
In order to answer the question, we need to have more information about the dilution factor of the tubes. Assuming that all the tubes have the same dilution factor, we can use the formula:C1V1 = C2V2
Where,C1 = concentration of the initial solution,V1 = volume of the initial solution,C2 = concentration of the final solution,V2 = volume of the final solution
Given that the concentration of the first tube is 150 ng/ml, we can use the above formula to calculate the concentrations of the other three tubes, provided we know the dilution factor.
Let's assume that the dilution factor is 10, which means that the initial volume was diluted by a factor of 10 to obtain the final volume in each tube.
Using the formula,C1V1 = C2V2
For tube 1, C1 = 150 ng/ml, V1 = 1 ml (assuming initial volume is 1 ml), C2 = concentration of tube 2, V2 = 0.1 ml (assuming a dilution factor of 10)
Substituting the values,150 x 1 = C2 x 0.1C2 = 1500 ng/ml
Therefore, the concentration of tube 2 is 1500 ng/ml.
Repeating the same process for the other two tubes, we get:C3 = 15000 ng/mlC4 = 150000 ng/ml
To know more about dilution factor visit:
https://brainly.com/question/30887569
#SPJ11
A restaurant built a ramp to make their facility more accessible to people in wheelchairs. They covered the entire surface of the ramp with metal to make it more durable.
How much metal did they use to cover the ramp, including the bottom?
Answers
The total surface area of the ramp is 300 square feet
To find out how much metal the restaurant used to cover the ramp, we need to know the length, width, and height of the ramp.
Let's assume that the ramp is a rectangular prism with a length of 20 feet, a width of 5 feet, and a height of 2 feet. To find the total surface area of the ramp, we need to calculate the area of each of the six faces and add them together.
The area of the bottom face is 20 feet × 5 feet = 100 square feet.
The area of the top face is also 100 square feet.
The area of each of the side faces is 2 feet × 20 feet = 40 square feet (there are two side faces).
The area of each of the end faces is 2 feet × 5 feet = 10 square feet (there are two end faces).
Therefore, the total surface area of the ramp is:
100 + 100 + 40 + 40 + 10 + 10 = 300 square feet
Since the restaurant covered the entire surface of the ramp with metal, they used 300 square feet of metal to cover the ramp, including the bottom.
Learn more about surface area here
https://brainly.com/question/28776132
#SPJ11
Jeffrey's mother gave him $58 to go to the store. Jeffrey bought 3 loaves of bread and 5 cartons of orange juice. Each loaf of bread cost $3 and each carton of orange juice cost $5. How much money does Jeffrey have left?
Answers
Answer:
3 loaves of bread ×$3 =$9
5cartons of orange juice×$5=$25
$9×$25=$34
$58-$34=$24
Answer:
35
Step-by-step explanation:
Which statement describes a series of transformationsthat would show that figureA is congruent to figure B.
PLEASE HELP!!!
I WILL GIVE BRAINLIEST

Answers
Answer:
MARK ME BRAINLIEST ps love: point stealer
The Smith family has 4 sons and 3 daughters. In how many ways can they be seated in a row of 7 chairs such that at least 2 boys are next to each other
Answers
There are 864 number of ways the Smith family can be seated in a row of 7 chairs such that at least 2 boys are next to each other.
To determine the number of ways the Smith family can be seated in a row of 7 chairs such that at least 2 boys are next to each other, we can consider different cases based on the arrangement of boys and girls.
Case 1: Two boys are seated together:
In this case, we can consider the two boys as a single entity.
Therefore, we have 6 entities: BB (boys together), B (single boy), B (single boy), G (girl), G (girl), G (girl). These entities can be arranged in 6! ways.
Case 2: Three boys are seated together:
In this case, we can consider the three boys as a single entity.
We have 5 entities: BBB (boys together), B (single boy), G (girl), G (girl), G (girl). These entities can be arranged in 5! ways.
Case 3: Four boys are seated together:
In this case, we can consider the four boys as a single entity.
We have 4 entities: BBBB (boys together), G (girl), G (girl), G (girl). These entities can be arranged in 4! ways.
To find the total number of arrangements, we sum up the arrangements from each case:
Total arrangements = 6! + 5! + 4!
Calculating the values:
6! = 720
5! = 120
4! = 24
Total arrangements = 720 + 120 + 24 = 864
To know more about number of ways refer here:
https://brainly.com/question/30649502#
#SPJ11
Question Answer O A True O B False Question Answer O A True O B False Question Answer OA O B True False Using logarithmic differentiation we obtain that the derivative of the function y = x2x² satisfies the equation y = 4x log x + 2x. y Using logarithmic differentiation we obtain that the derivative of the function (1+x²)2 (1 + sin x)² y= 1-x² satisfies the equation 4x 2cos x 2x -= + y 1 + x² 1 + sin x 1-x² Given two complex numbers z=3-1 and w=3+ the product z2w equals 30-10%. Y'
Answers
In the first question, the statement "Using logarithmic differentiation we obtain that the derivative of the function y = x² satisfies the equation y = 4x log x + 2x" is true.
In the first question, using logarithmic differentiation on the function y = x², we differentiate both sides, apply the product rule and logarithmic differentiation, and simplify to obtain the equation y = 4x log x + 2x, which is correct.
In the second question, the statement is false. When using logarithmic differentiation on the function y = (1+x²)²(1 + sin x)²/(1-x²), the derivative is calculated correctly, but the equation given is incorrect. The correct equation after logarithmic differentiation should be y' = (4x/(1 + x²)(1 + sin x))(1-x²) - (2x(1+x²)²(1 + sin x)²)/(1-x²)².
In the third question, the product z²w is calculated correctly as 30-10%.
It is important to accurately apply logarithmic differentiation and perform the necessary calculations to determine the derivatives and products correctly.
Learn more about Logarithmic differentiation: brainly.com/question/30881276
#SPJ11