Answers
Answer: x= -3 + 2\(\sqrt{2\\}\) or -3 -2 \(\sqrt{2}\)
Step-by-step explanation:
First you want to get the quadratic formula
in this case a=1 b=6 and c=1
plug it in and solve the equations
(sorry don't know how to put in equations here)
Answer:
Answer: x= -3 + 2\sqrt{2\\} or -3 -2 \sqrt{2}
Step-by-step explanation:
First you want to get the quadratic formula
in this case a=1 b=6 and c=1
plug it in and solve the equations
Related Questions
Please help me please

Answers
Answer:
\(-\frac{1}{64}\)
Step-by-step explanation:
Evaluate the following limit.
\(\lim_{x \to 0} \frac{\frac{1}{x+8} -\frac{1}{8} }{x}\)
(1) - Simplify the limit
\(\lim_{x \to 0} \frac{\frac{1}{x+8} -\frac{1}{8} }{x}\\\\\Longrightarrow \lim_{x \to 0} \frac{\frac{1(8)}{(x+8)(8)} -\frac{1(x+8)}{8(x+8)} }{x}\\\\\Longrightarrow \lim_{x \to 0} \frac{\frac{8-x-8}{8(x+8)} }{x} \\\\\Longrightarrow \lim_{x \to 0} \frac{\frac{ -x}{8(x+8)} }{x} \\\\\Longrightarrow \lim_{x \to 0} \frac{-x}{8x(x+8)} \\\\\Longrightarrow \boxed{\lim_{x \to 0} \frac{-1}{8(x+8)} }\)
(2) - Plug in the limit
\(\lim_{x \to 0} \frac{-1}{8(x+8)}\\\\\Longrightarrow \lim_{x \to 0} \frac{-1}{8((0)+8)}\\\\\Longrightarrow \lim_{x \to 0} \frac{-1}{8(8)} \\\\\therefore \boxed{\boxed{\lim_{x \to 0} \frac{\frac{1}{x+8} -\frac{1}{8} }{x}=-\frac{1}{64} }}\)
Find the value of x.

Answers
it is 80.
so for starters you draw yourself two triangels. than you can get z angle by substracting 70+90 from 180 and you get 40 degrees. after that you substract 50+90 from 180 and you get y=60 degrees. lastly you see that x+y+z=180 so 180-60-40=x=80 degrees

Answer:
\( \sf \: x = 60°\)
Step-by-step explanation:
Now we have to,
→ find the required value of x.
Forming the equation,
→ 70° + x + 50° = 180°
Now the value of x will be,
→ 70° + x + 50° = 180°
→ (70° + 50°) + x = 180°
→ 120° + x = 180°
→ x = 180° - 120°
→ [ x = 60° ]
Hence, the value of x is 60°.
Consider a sequence defined by the explicit rule f(n)=-8+3 (n − 1). Choose True or False for each statement.

Answers
Given the general n th term of the sequence,
\(f(n)=-8+3(n-1)\)For n = 1,
\(\begin{gathered} f(1)=-8+3(1-1) \\ =-8 \end{gathered}\)Therefore, the first statement is true.
Now for n = 2,
\(\begin{gathered} f(2)=-8+3(2-1) \\ =-8+3 \\ =-5 \end{gathered}\)Therefore, the first two terms of the sequence is -8 and -5.
So, the common difference is,
\(-5-(-8)=-5+8=3\)Therefore, the common difference is 3.
So, the second statement is true.
Now fifth term is for n = 5.
Therefore,
\(\begin{gathered} f(5)=-8+3(5-1) \\ =-8+(3\times4) \\ =-8+12 \\ =4 \end{gathered}\)Therefore the fifth term is 4 but not 7.
Hence, the third statement is false.
Determine the value of x.

Answers
Answer:
x = 4.59
Step-by-step explanation:
Since this is a right triangle, we can use trig functions
tan theta = opp / adj
tan 74 = 16/ x
x tan 74 = 16
x = 16/ tan 74
x=4.58792
\(\huge\text{Hey there!}\)
\(\boxed{\boxed{\huge\text{Formula: \boxed{\text{tan } \theta = \mathsf{\dfrac{Opposite}{Adjacent}}}}}}\)
\(\boxed{\huge\text{\boxed{\mathsf{\bold{tan\ 74} = \dfrac{16}{x}}}}}\)
\(\boxed{\boxed{\huge\textsf{x tan 74 equals \bf 16}}}\)
\(\boxed{\huge\text{x = }\boxed{\mathsf{\dfrac{16}{tan \ 74}}}}\)
\(\boxed{\boxed{\huge\text{x = \bf x=4.58792}}}\boxed{\boxed{\huge\text{\bf (ORIGINALLY)}}}\)
\(\boxed{\boxed{\huge\text{x = \boxed{\bf 4.58792\ or \ 4.58 \ is \approx \underline{\underline{4.59}}}}}}\huge\checkmark\)
\(\boxed{\boxed{\huge\text{Therefore, your answer is: \boxed{\textsf{Option C. \bf 4.59}}}}}\huge\checkmark\)
\(\huge\text{\huge\text{Good luck on your assignment \& enjoy your day!}}\)
~\(\boxed{\huge\text{\boxed{\frak{Amphitrite1040:)}}}}\)
60 point Pls someone
Indicate which property is illustrated in Step 1.
Step 1
5x +8+7x + 1=(5x + 8)+(7x+1)
Step 2 = 5x + (8 + 7x) + 1
Step 3 = 5x + (7x + 8) + 1
Step 4 = (5x + 7x) + (8 + 1)
Step 5 = (5 + 7)x + (8 + 1)
Step 6 = 12x + 9
A. associative
B. commutative
C. arithmetic fact
D. distributive
Answers
A. associative
associative property which describes the numbers in a multiplication expression can be regrouped using parentheses.
for example: 2x² + 5x + 3 ↔ ( x + 1 ) ( 2x + 3 )
(A)•
•Hope this helps!•
Have a wonderful day!•~
An angle measures 64 degrees less than the measure of its complementary angle. What is the measure of each angle?
Answers
Answer:
13, 77
Step-by-step explanation:
complementary angle = 90
90 = x+x+64
90=2x+64
x=13
x+64=77
The sum of the base and the height of a triangle is 20 cm. Find the dimensions for which the area is a maximum.
Answers
Answer:
base = 10cm and height = 10cm
Step-by-step explanation:
base + height = 20
base = height = 20/2= 10cm
A population of unknown shape has a mean of 75 . Forty samples from this population are selected and the standard deviation of the sample is 5. Determine the probability that the sample mean is (i). less than 74. (ii). between 74 and 76 .
Answers
To determine the probability that the sample mean falls within certain ranges, we can use the Central Limit Theorem, which states that for a large enough sample size, the distribution of sample means will approach a normal distribution regardless of the shape of the population.
Given that the population mean is 75 and the standard deviation of the sample is 5, we can assume that the population standard deviation is also 5 (since it is not explicitly given).
(i) Probability that the sample mean is less than 74:
To calculate this probability, we need to standardize the sample mean using the formula for the standard error of the mean (SEM):
SEM = population standard deviation / √sample size
In this case, SEM = 5 / √40 ≈ 0.7906.
Next, we can calculate the z-score corresponding to the sample mean of 74 using the formula:
z = (sample mean - population mean) / SEM
z = (74 - 75) / 0.7906 ≈ -1.263
Using a standard normal distribution table or a calculator, we can find the probability associated with a z-score of -1.263. Let's denote this probability as P(Z < -1.263).
(ii) Probability that the sample mean is between 74 and 76:
To calculate this probability, we need to find the probabilities for both ends and then subtract them.
Using the same standard error of the mean (SEM) as before, we can calculate the z-scores for the lower and upper bounds:
z_lower = (74 - 75) / 0.7906 ≈ -1.263
z_upper = (76 - 75) / 0.7906 ≈ 1.263
Let's denote the probabilities associated with these z-scores as P(Z < -1.263) and P(Z < 1.263), respectively.
The probability that the sample mean is between 74 and 76 can be calculated as:
P(74 < sample mean < 76) = P(Z < 1.263) - P(Z < -1.263)
Using a standard normal distribution table or a calculator, we can find the probabilities P(Z < -1.263) and P(Z < 1.263), and then subtract them to obtain the desired probability.
Note: It is important to remember that the Central Limit Theorem assumes a large enough sample size for the approximation to a normal distribution to hold. In this case, with a sample size of 40, the assumption is reasonable.
To learn more about probability: -brainly.com/question/31828911
#SPJ11
To determine the probability that the sample mean falls within a certain range, we can use the Central Limit Theorem and the properties of the normal distribution.
(I) Probability that the sample mean is less than 74:
Since the sample size is large (n = 40), according to the Central Limit Theorem, the distribution of the sample mean will be approximately normal. We can calculate the z-score corresponding to 74 using the formula:
z = (X - μ) / (σ / √n)
where X is the sample mean, μ is the population mean, σ is the population standard deviation, and n is the sample size.
In this case, X= 74, μ = 75, σ = 5, and n = 40. Plugging these values into the formula, we get:
z = (74 - 75) / (5 / √40) ≈ -1.264
We can then use a standard normal distribution table or a calculator to find the probability associated with this z-score. The probability that the sample mean is less than 74 is the cumulative probability up to the z-score -1.264.
(ii) Probability that the sample mean is between 74 and 76:
To find the probability that the sample mean falls within a range, we need to calculate the z-scores for both endpoints of the range and then find the difference between their cumulative probabilities.
For the lower endpoint, z = (74 - 75) / (5 / √40) ≈ -1.264 (same as in part (I)).
For the upper endpoint, z = (76 - 75) / (5 / √40) ≈ 1.264 (opposite sign of lower endpoint).
We can then find the cumulative probabilities for both z-scores using a standard normal distribution table or a calculator. The probability that the sample mean is between 74 and 76 is the difference between the cumulative probabilities of the upper and lower z-scores.
To learn more about Central Limit Theorem: -brainly.com/question/898534
#SPJ11
Main St. Fair thinks your wheel is broken – the 3 outcomes (Big, Small, and No prize) are not coming out exactly equal. Your wheel maker says that’s normal – the numbers should be close to each other but probably not exactly equal. Who do you think is right? Explain.
Answers
Answer:
Step-by-step explanation:
Points J and Kare midpoints of the sides of triangle
FGH.
What is the value of y

Answers
Answer:
7
Step-by-step explanation:
As we can see, the sides of the bigger triangle is twice that or the smaller
Thus, we have it that for similar sides, we simply have to multiply the smaller side length by 2 to give the larger
We have this as:
2(2y + 5) = 5y + 3
4y + 10 = 5y+ 3
5y-4y = 10-3
y = 7
Point (∃xP(x)∧Q(x))≡∃x(P(x)∧Q(x)) Q6 1 Point Which rule of ND justifies P(0) from ∀xP(x) ? There is no rule of ND that justifies this. (∀E) (∀I) (∃E) (∃I)
Answers
The (∃E) rule is used to infer P(0) from ∀xP(x), and this conclusion is supported by the existence of an object that satisfies the predicate.
The rule of natural deduction that justifies P(0) from ∀xP(x) is the existential elimination (∃E) rule. This rule allows us to infer a particular instance of an existential quantification based on the existence of an object that satisfies the predicate. In this case, since we have the universal quantification ∀xP(x), we can use (∃E) to conclude P(0) by substituting 0 for x. By doing so, we have shown that there exists an object, namely 0, that satisfies the predicate P(x). Therefore, (∃E) justifies the statement P(0) from the given universal quantification.
To know more about existence, visit:
https://brainly.com/question/31869763
#SPJ11
help how to do it i dont know what to do

Answers
Answer:
Step-by-step explanation:
1 2 and 4 I Think
2x-5=7
solve for x
please include explanation
Answers
Answer:
x=6
Step-by-step explanation:
2x-5=7
add 5 to both sides
so the -5 cancels out on this side because -5+5=0
on the other side 7+5=12
which means:
2x=12
to get rid of the 2 we need to divided each side by 2
so...
x=6 as 12 divided by 2 is 6 and 2x divided by 2 is just x
this leaves us with x=6
:)
Answer: x = 6
Step-by-step explanation:
2*6 =12
12 - 5 = 7
Sorry i don't really know how to explain it
HELP!!
Ingrid and Harish were trying to solve the equation:
x^2-3x=x+1
Ingrid said, “First, I'll subtract x from both sides so I have x^2-4x=1. Then I can solve by completing the square. If I add 4 to each side, I can rewrite the equation as (x-2)^2=5. Harish said, “I'll isolate the x^2x term by adding 3x to both sides of the equation. Then I'll solve by taking the square root.”
Whose solution strategy would work?
Answers
Answer:
only ingrid
Step-by-step explanation:
Let L : R^2 → R^3 with (x,y) → (x,y,x^2 + y^2)
Let P be a set of points in general position in the plane, and let
L (P) the set of image points of P under the mapping L .
Assertion:
The convex hull CH (L P)) of the
image points of P in R^3 contains at least as many edges as any triangulation of P in the plane.
Is this true?
Justify your answer.
Answers
The assertion is true stating that the convex hull CH (L P)) of the image points of P in R^3 contains at least as many edges as any triangulation of P in the plane.
To prove this, we will use the following lemma:
Lemma: Let S be a set of points in the plane, and let T be the set of image points of S under the mapping L. If three points in S are not collinear, then the corresponding image points in T are not coplanar.
Proof of Lemma: Suppose that three points p1, p2, and p3 in S are not collinear. Then their images under L are (x1, y1, z1), (x2, y2, z2), and (x3, y3, z3), respectively. Suppose for contradiction that these three points are coplanar.
Then there exist constants a, b, and c such that ax1 + by1 + cz1 = ax2 + by2 + cz2 = ax3 + by3 + cz3. Subtracting the second equation from the first yields a(x1 - x2) + b(y1 - y2) + c(z1 - z2) = 0. Similarly, subtracting the third equation from the first yields a(x1 - x3) + b(y1 - y3) + c(z1 - z3) = 0.
Multiplying the first equation by z1 - z3 and subtracting it from the second equation multiplied by z1 - z2 yields a(x2 - x3) + b(y2 - y3) = 0. Since p1, p2, and p3 are not collinear, it follows that x2 - x3 ≠ 0 or y2 - y3 ≠ 0.
Therefore, we can solve for a and b to obtain a unique solution (up to scaling) for any choice of x2, y2, z2, x3, y3, and z3. This implies that the points in T are not coplanar, which completes the proof of the lemma.
Now, let P be a set of points in general position in the plane, and let T be the set of image points of P under L. Let CH(P) be the convex hull of P in the plane, and let CH(T) be the convex hull of T in R^3. We will show that CH(T) contains at least as many edges as any triangulation of P in the plane.
Let T' be a subset of T that corresponds to a triangulation of P in the plane. By the lemma, the points in T' are not coplanar. Therefore, CH(T') is a polyhedron with triangular faces. Let E be the set of edges of CH(T').
For each edge e in E, let p1 and p2 be the corresponding points in P that define e. Since P is in general position, there exists a unique plane containing p1, p2, and some other point p3 ∈ P that is not collinear with p1 and p2. Let t1, t2, and t3 be the corresponding image points in T. By the lemma, t1, t2, and t3 are not coplanar. Therefore, there exists a unique plane containing t1, t2, and some other point t4 ∈ T that is not coplanar with t1, t2, and t3. Let e' be the edge of CH(T) that corresponds to this plane.
We claim that every edge e' in CH(T) corresponds to an edge e in E. To see this, suppose for contradiction that e' corresponds to a face F of CH(T'). Then F is a triangle with vertices t1', t2', and t3', say. By the lemma, there exist points p1', p2', and p3' in P such that L(p1') = t1', L(p2') = t2', and L(p3') = t3'.
Since P is in general position, there exists a unique plane containing p1', p2', and p3'. But this plane must also contain some other point p4 ∈ P, which contradicts the fact that F is a triangle. Therefore, e' corresponds to an edge e in E.
Since every edge e' in CH(T) corresponds to an edge e in E, it follows that CH(T) contains at least as many edges as any triangulation of P in the plane. This completes the proof of the assertion.
To know more about convex hull refer here :
https://brainly.com/question/30453139#
#SPJ11
A company claims that 9 out of 10 doctors (i.e. 90% ) recommend its brand of couph syrup to their patients. To test this claim against the alternative that the actual proportion is fess than 90%, a random sample of 200 doctors was chosen which results in 175 who indicate that they recommend this cough syrup. Find the standardized test statistic, z. Round to two decimal places. Hint: Do not forget the sign on your answer!
Answers
The standardized test statistic (z) for the given scenario is approximately -1.18, indicating a deviation from the claimed proportion.
To find the standardized test statistic (z), we can use the formula:
z = (p - P) / sqrt(P(1 - P) / n)
Where:
p is the observed proportion (175/200 = 0.875),
P is the claimed proportion (0.90),
n is the sample size (200).
Substituting the values into the formula:
z = (0.875 - 0.90) / sqrt(0.90 * (1 - 0.90) / 200)
Simplifying the expression inside the square root:
z = (0.875 - 0.90) / sqrt(0.09 / 200)
z = -0.025 / sqrt(0.00045)
Calculating the square root:
z = -0.025 / 0.02121
z ≈ -1.18
Rounding to two decimal places, the standardized test statistic (z) is approximately -1.18.
To learn more about test statistic (z) click here: brainly.com/question/30754810
#SPJ11
Help me out please. Easy points

Answers
Answer: 12/15
Step-by-step explanation:
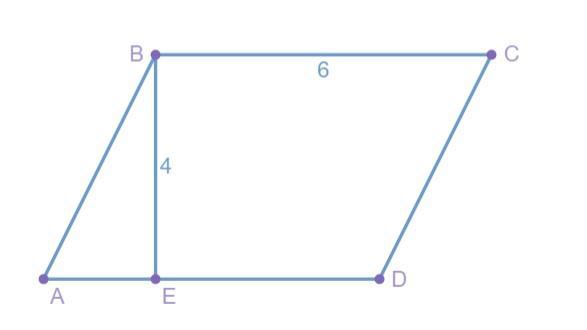
What is the area of the parallelogram? You can press the button below the parallelogram to see it decomposed into a rectangle to help.
The area of the parallelogram is
square units. on zearn
Answers
The area of the parallelogram in square units will be 24 square units.
Given that:
Height, H = 4 units
WIdth, W = 6 units
Let H be the height and W be the width of the parallelogram. Then the area of the parallelogram will be given as,
Area of the parallelogram = H × W square units
The area of the parallelogram is calculated as,
A = 4 x 6
A = 24 square units
More about the area of the parallelogram link is given below.
https://brainly.com/question/16052466
#SPJ1
The missing diagram is given below.
Which is the graph of the inequality?
3y−9x≥9
Number graph ranging from negative ten to ten on the x and y axes. A dotted line passes through (zero, negative two) and (five, negative three). The area above the line is shaded gray.
Number graph ranging from negative ten to ten on the x and y axes. A solid line passes through (negative one, zero) and (zero, three). The area to the left of the line is shaded gray.
Number graph ranging from negative twenty to twenty in increments of two on the x and y axes. A solid line passes through (zero, negative fourteen) and (two, zero). The area to the right of the line is shaded gray.
Number graph ranging from negative twenty to twenty in increments of two on the x and y axes. A dotted line with a positive slope is drawn in the fourth quadrant of the graph. The area above the line is shaded gray.
Answers
A solid line passes through (-1, 0) and (0, 3). The area to the left of the line is shaded gray.
How to get the graph of the inequality?
Here we have the inequality:
3y - 9x ≥ 9
First, we should isolate y on one side of the inequality.
3y ≥ 9x + 9
y ≥ 3x + 3
Then, the graph will be a solid line of the form:
y = 3x + 3
Where the line is solid because the points on the line are solutions, and we need to shade all the region above the line.
Also, notice that for the line:
y = 3x + 3
if x = -1 we have:
y = 3*(-1) + 3 = 0
if x = 0 we have:
y = 3*0 + 3 = 3
Then the line passes through (0, 3) and (-1, 0). So the correct option is the second one.
"Number graph ranging from negative ten to ten on the x and y axes. A solid line passes through (negative one, zero) and (zero, three). The area to the left of the line is shaded gray."
If you want to learn more about inequalities:
https://brainly.com/question/18881247
#SPJ1
Function \(y = f(x)\) is continuous on \(R\).
The function satisfy \(f(x)+x=\int\limits^2_0 {[f(x)-x]} \, dx\)
∀\(x\)∈\(R\).
Find the value of m so that \(\int\limits^2_0 {[mx+f(x)]} \, dx=0\).
A. m = -2
B. m = 0
C. m = -3
D. m = -1
Answers
The value of m so that the condition satisfies is -2, the correct option is A.
We are given that;
y=f(x) is continuous
Now,
To find the numbers c that satisfy the conclusion of the Mean Value Theorem, we need to solve the equation:
f’© = [f(2) - f(0)] / (2 - 0)
f’(x) = 8x - 2
f(2) = 4(2)^2 - 2(2) + 3 = 23
f(0) = 4(0)^2 - 2(0) + 3 = 3
f’© = (23 - 3) / (2 - 0)
f’© = 10
8m - 2 = 10
8m = 12
m = 12/8
m = -2
Therefore, by the given function the answer will be -2.
Learn more about function here:
https://brainly.com/question/2253924
#SPJ1
Circle a has a radius of 17 inches. what is the circumference of circle a?
Answers
Answer:
106,81 inch ..............
The formulae for the circumference is 2*pi*r
Meaning 2 X 17 which is 32 and 32 X pi is 32*pi
Find the measure of each angle indicated.
A) 21°
C) 23
E) 25°
B) 80°
D) 20°

Answers
Answer:
D) 20⁰
Step-by-step explanation:
EDF = 180-100=80⁰
EFD= 80⁰+80⁰=160⁰
180⁰-160⁰=20⁰
Answer:
I would say D, 20°
Step-by-step explanation:
angles on a straight line should be equal to 180°. so 180 -100 = 80° inside.
angles inside a triangle should also be 180. So, 80° + 80° =160°. to get the other angle subtract 160 from 180 to get 20°
Can y’all help plsss

Answers
Answer:
ok so a way to do this is that
124-180=56
75-180=105
105+56= 161
180-161= 19
180-19=161
so A.
Please mark Brainliest if helpful! :))
Find the complex numbers
please specify which answers are which



Answers
The complex number in each case will be 11 - 3i, 2 + i, and 5 - 6i.
What is a complex number?The complex number is the combination of the real part and the imaginary part. Then the complex number is given as a+bi where the value of i is √(-1) and the value of i² is -1.
The real part is 11 and the imaginary part is -3i. Then the complex number is given as,
⇒ 11 - 3i
The real part is 2 and the imaginary part is i. Then the complex number is given as,
⇒ 2 + i
The real part is 5 and the imaginary part is -6√(-1). Then the complex number is given as,
⇒ 5 - 6√(-1)
⇒ 5 - 6i
The complex number in each case will be 11 - 3i, 2 + i, and 5 - 6i.
More about the complex number link is given below.
https://brainly.com/question/10251853
#SPJ1
The blueprint of a triangular patio has side lengths 4.5 in., 4.5 in., and 6.75 in. If the shorter sides of the actual patio are each 22.5 ft long, how long is the third side?
Answers
The blueprint of the patio is a scaled-down version of the actual patio. The scale factor between the blueprint and the actual patio is 22.5 ft / 4.5 in = 5 ft/in. Therefore, the third side of the actual patio is 6.75 in × 5 ft/in = 33.75 ft long.
What is the surface area of the cylinder with height 8 m and radius 4 m? Round your answer to the nearest thousandth.
Answers
\(\textit{surface area of a cylinder}\\\\ SA=2\pi r(h+r)~~ \begin{cases} r=radius\\ h=height\\[-0.5em] \hrulefill\\ h=8\\ r=4 \end{cases}\implies SA=2\pi (4)(8+4) \\\\\\ SA=8\pi (12)\implies SA=96\pi \implies SA\approx 301.593~m^2\)
A babysitter charges an hourly rate. The equation y = 12x represents the relationship between hours of babysitting, x, and total pay, y, in
dollars.
What is the salary per hour for the babysitter?
Answers
salary : $12 per hour
How Solve the following questions (write all steps). Q1: Use the following data to find a recursive Nevill's method When interpdating table using Polynomial at x-4.1 f(x) X 36 1.16164956 3.8 080201036 4.0 0.30663842 4.2 035916618 -123926000. 4.4 Q2: Construct an approximation polynomial for the following data using Hermite method. 1 f(x) f'(x) x 1.2 2.572152 7.615964 1.3 3.60 2102 13-97514 1.4 5.797884 34.61546 1.5 14.101442 199.500 - Good Luck -
Answers
To find a recursive Nevill's method when interpolating a table using a polynomial at x = 4.1, we can use the following steps:
Step 1: Set up the given data in a table with two columns, one for f(x) and the other for x.
f(x) x
36 1.16164956
3.80201036 4.0
0.30663842 4.2
0.35916618 -123926000.4
Step 2: Begin by finding the first-order differences in the f(x) column. Subtract each successive value from the previous value.
Δf(x) x
-32.19798964 1.16164956
-3.49537194 4.0
-0.05247276 4.2
Step 3: Repeat the process of finding differences until we reach a single value in the Δf(x) column. Continue subtracting each successive value from the previous one.
Δ^2f(x) x
29.7026177 1.16164956
3.44289918 4.0
Step 4: Repeat Step 3 until we obtain a single value.
Δ^3f(x) x
-26.25971852 1.16164956
Step 5: Calculate the divided differences using the values obtained in the previous steps.
Divided Differences:
Df(x) x
36 1.16164956
-32.19798964 4.0
29.7026177 4.2
-26.25971852 -123926000.4
Step 6: Apply the recursive Nevill's method to find the interpolated value at x = 4.1 using the divided differences.
f(4.1) = 36 + (-32.19798964)(4.1 - 1.16164956) + (29.7026177)(4.1 - 1.16164956)(4.1 - 4.0) + (-26.25971852)(4.1 - 1.16164956)(4.1 - 4.0)(4.1 - 4.2)
Solving the above expression will give the interpolated value at x = 4.1.
Q2: To construct an approximation polynomial using the Hermite method, we follow these steps:
Step 1: Set up the given data in a table with three columns: f(x), f'(x), and x.
f(x) f'(x) x
2.572152 7.615964 1.2
3.602102 13.97514 1.3
5.797884 34.61546 1.4
14.101442 199.500 1.5
Step 2: Calculate the divided differences for the f(x) and f'(x) columns separately.
Divided Differences for f(x):
Df(x) \(D^2\)f(x) \(D^3\)f(x)
2.572152 0.51595 0.25838
Divided Differences for f'(x):
Df'(x) \(D^2\)f'(x)
7.615964 2.852176
Step 3: Apply the Hermite interpolation formula to construct the approximation polynomial.
Learn more about polynomial here:
https://brainly.com/question/11536910
#SPJ11
To encourage recycling, the people of Rome, Italy, built a model of Basilica di San Pietro from empty beverage cans. The model was built to a 1: 5 scale and was a rectangular prism that measured 26 meters high, 49 meters wide, and 93 meters long. Find the dimensions of the actual Basilica di San Pietro. (Lesson 12-8)
Answers
The dimensions of the actual Basilica di San Pietro in Rome, Italy are 130 meters high, 245 meters wide, and 465 meters long.
How can we determine the dimensions of the actual Basilica di San Pietro based on the scale model made from empty beverage cans?To find the dimensions of the actual Basilica di San Pietro, we can use the scale ratio between the model and the real structure. The scale given is 1:5, which means that each dimension of the model is one-fifth of the corresponding dimension of the actual basilica.
Given that the model measures 26 meters high, 49 meters wide, and 93 meters long, we can multiply each dimension by the scale ratio of 5 to find the dimensions of the actual basilica.
Height: 26 meters ˣ 5 = 130 meters
Width: 49 meters ˣ 5 = 245 meters
Length: 93 meters ˣ 5 = 465 meters
Therefore, the actual Basilica di San Pietro in Rome, Italy has dimensions of approximately 130 meters in height, 245 meters in width, and 465 meters in length.
Learn more about: dimensions
brainly.com/question/31460047
#SPJ11
use spherical coordinates to calculate the triple integral of f(x, y, z)=x2 y2 over the region rho≤2.
Answers
Spherical coordinates are a system of coordinates that describe points in three-dimensional space using a distance from the origin, an angle of inclination from the positive z-axis, and an angle of rotation around the z-axis.
To calculate the triple integral of f(x, y, z)=x2 y2 over the region rho≤2 using spherical coordinates, we first need to express the function in terms of the spherical coordinates.
We know that in spherical coordinates,
x = ρ sin(φ) cos(θ)
y = ρ sin(φ) sin(θ)
z = ρ cos(φ)
where ρ is the radial distance, θ is the azimuthal angle, and φ is the polar angle.
So, f(x, y, z) = x2 y2 can be expressed as
f(ρ, φ, θ) = (ρ sin(φ) cos(θ))2 (ρ sin(φ) sin(θ))2
= ρ4 sin2(φ) cos2(θ) sin2(φ) sin2(θ)
= ρ4 sin4(φ) cos2(θ)
Now, we can set up the triple integral using spherical coordinates.
∫∫∫ f(ρ, φ, θ) ρ2 sin(φ) dρ dφ dθ
= ∫0^2π ∫0^π/2 ∫0^2 f(ρ, φ, θ) ρ2 sin(φ) dρ dφ dθ
= ∫0^2π ∫0^π/2 ∫0^2 ρ4 sin4(φ) cos2(θ) ρ2 sin(φ) dρ dφ dθ
= ∫0^2π ∫0^π/2 ∫0^2 ρ6 sin5(φ) cos2(θ) dρ dφ dθ
= ∫0^2π ∫0^π/2 [ρ7/7 sin5(φ) cos2(θ)]0^2 dφ dθ
= ∫0^2π ∫0^π/2 32/7 sin5(φ) cos2(θ) dφ dθ
= 32/7 ∫0^2π cos2(θ) dθ ∫0^π/2 sin5(φ) dφ
= 32/7 [π sin6(π/2)/6]
= 32π/21
Therefore, the triple integral of f(x, y, z) = x2 y2 over the region rho≤2 using spherical coordinates is 32π/21.
To know more about Spherical coordinates visit:
https://brainly.com/question/4465072
#SPJ11
