Answers
In the pic
Step-by-step explanation:
If you have any questions about the way I solved it, don't hesitate to ask me in the comments below ;)

Related Questions
Write a recursive formula to generate an arithmetic sequence with a first term 6 and a
common difference 3.2. Find the 10th term,
Answers
Answer:Recursive formulas give us two pieces of information: The first term of the sequence. The pattern rule to get any term from the term that comes before it.
Step-by-step explanation:
a textbook company claims that their book is so engaging that more than 55% of students read it. if a hypothesis test is performed that rejects the null hypothesis, how would this decision be interpreted? group of answer choices there is not sufficient evidence to support the claim that no more than 55% of students read this text there is sufficient evidence to support the claim that no more than 55% of students read this text there is sufficient evidence to support the claim that more than 55% of students read this text there is not sufficient evidence to support the claim that more than 55% of students read this text
Answers
The correct answer is "There is sufficient evidence to support the claim that more than 55% of students read this text".
In hypothesis testing, null hypothesis is a statement of no effect or no difference. In this case, null hypothesis is that percentage of students who read the textbook is equal to or less than 55%. If null hypothesis is rejected it means that there is sufficient evidence to support the alternative hypothesis which in this case is that the percentage of students who read the textbook is greater than 55%.
So, in this case if hypothesis test is performed and the null hypothesis is rejected it can be interpreted that there is sufficient evidence to support the claim that more than 55% of students read this text.
Learn more about Hypothesis Testing at:
https://brainly.com/question/30588452
#SPJ4
A polar graph is shown.
polar graph in a ring, which is mostly below the horizontal axis with a depression
Which of the following equations represents the graph?

Answers
The equation of the polar graph is r = 2 + 3cosθ
What is a polar graph?A polar graph is the pictorial representation of a polar curve
Since we have the polar graph shown in the figure, it is a polar graph in a ring, which is mostly below the horizontal axis with a depression. To determine which of the following equations represents the graph, we proceed as follows.
We know that this type of polar graph has the general equation r = a + bcosθ.
So, the only equation which satisfies this condition is r = 2 + 3cosθ.
So, the equation is r = 2 + 3cosθ
Learn more about equation of polar graph here:
https://brainly.com/question/31739442
#SPJ1
seven family members who are potential kidney donors. How many possible orders are there for a best match, a second-best match, and a third-best match
Answers
If there are seven family members who are potential kidney donors, the number of possible orders for a best match, a second-best match, and a third-best match can be calculated using the concept of permutations.
Since each match is selected from the remaining available donors after the previous match, the number of possibilities decreases by one for each match.
For the best match, there are 7 possible donors.
For the second-best match, there are 6 remaining donors.
For the third-best match, there are 5 remaining donors.
To calculate the total number of possible orders, we multiply these numbers together:
Total number of possible orders = 7 * 6 * 5 = 210
Therefore, there are 210 possible orders for a best match, a second-best match, and a third-best match from the seven family members who are potential kidney donors.
Learn more about permutations here:
https://brainly.com/question/32683496
#SPJ11
Sam completed the square for the quadratic equation y=1/2x^2−2x+3 in order to determine the minimum value of the equation, as shown.
Answers
Answer:
\((2,1)\)
Step-by-step explanation:
You can just use the formula \(x=-\frac{b}{2a}\):
\(y=ax^2+bx+c\)
\(y=\frac{1}{2}x^2-2x+3\)
\(x=-\frac{-2}{2(\frac{1}{2})}=\frac{2}{1}=2\)
\(y=\frac{1}{2}(2)^2-2(2)+3=\frac{1}{2}(4)-4+3=2-4+3=-2+3=1\)
Therefore, the minimum value of the equation is \((2,1)\)
25 POINTS IF U ANSWER THIS

Answers
The values of the variables x and y are 12 and 3 respectively, while the measure of angles m∠A and m∠B are 36° and 126° respectively
How to to evaluate for the values of variables and angles1). m∠A and m∠D are complementary angles so their sum is equal to 90°
3x + (4x + 6)° = 90°
7x = 90° - 6°
x = 84/7
x = 12
2). m∠A = 3(12) = 36°
3). m∠B and m∠C are on a straight line and their sum is equal to 180° {also called supplementary angles}.
18y + 42y = 180°
60y = 180°
y = 180°/60°
y = 3
4). m∠C = 42(3) = 126°
In conclusion, the values of the variables x and y are 12 and 3 respectively, while the measure of angles m∠A and m∠B are 36° and 126° respectively
Read more about angles here:https://brainly.com/question/1475130
#SPJ1
A hall has 22 rows of chairs there are 18 chairs in each row how many extra rows of chairs are needed to seat 468
Answers
Answer:
Total chairs = 18×22= 396
so no. of extra chairs need = 468-396 = 72
Now( 72/18) rows = 4 rows
Therefore 4 more rows are needed here
Hope it helps you
Answer: 4
Step-by-step explanation:
The amount of chairs in the hall can be found by multiplying 22 by 18 and getting 396. The amount of chairs needed is 468, so 468-396 gets you the amount of chairs still needed and the number 72. There are 18 chairs in each row, and 72/18 is 4. So 4 more rows are needed.
: Prove that a) X'Y' + X'Y +XY = X' +Y b) A'BC' + ABC' + BC'D = BC' Find the complement of the following function a) WX(Y'Z+YZ') + W'X'(Y' +Z)(Y+Z') b) (A+B'+C') (A'B' +C)(A + B'C') Find Dual of question 2 (a, b),
Answers
a) X'Y' + X'Y + XY simplifies to X' + Y.
b) A'BC' + ABC' + BC'D simplifies to BC'.
Complement of the functions:
a) Complement is W' + X' + YZ.
b) Complement is (A' + B + C)(A'B' + C' + A'B).
a) To prove X'Y' + X'Y + XY = X' + Y, we can use Boolean algebra identities:
X'Y' + X'Y + XY
= Y'(X' + X) + XY(Distributive Law)
= Y' + XY(X + X' = 1)
= X' + Y(Commutative Law)
Therefore, X'Y' + X'Y + XY simplifies to X' + Y.
b) To prove A'BC' + ABC' + BC'D = BC', we can simplify the expression using Boolean algebra:
A'BC' + ABC' + BC'D
= BC'(A' + A) + BC'D (Distributive Law)
= BC' + BC'D(A + A' = 1)
= BC'(BC' + BC'D = BC' + BC'(1) = BC')
Hence, A'BC' + ABC' + BC'D simplifies to BC'.
Complement of the given functions:
a) The complement of WX(Y'Z + YZ') + W'X'(Y' + Z)(Y + Z') is W' + X' + YZ.
b) The complement of (A + B' + C')(A'B' + C)(A + B'C') is (A' + B + C)(A'B' + C' + A'B).
Learn more About Distributive Law from the given link
https://brainly.com/question/25224410
#SPJ11
What is the surface area of the cylinder shown below? Use 3.14 for π. A. 660 cm2 B. 863 cm2 C. 353.25 cm2 D. 785 cm2
Answers
Answer:
602.88cm²
Step-by-step explanation:
Find the image of the cylinder attached
Surface area of a cylinder = A=2πrh+2πr²
r is the radius = 4cm
Height h = 20cm
Substitute
A = 2πr(r+h)
A = 2π(4)(4+20)
A = 8π(24)
A = 192π
A = 192(3.14)
A = 602.88cm²
Hence the surface area of the cylinder is 602.88cm²

Which of the following is equivalent to the expression below?
3(5-2i)
Answers
Answer: 15 - 6i
Step-by-step explanation:
3(5-2i)
3×5+3×(−2i)
Do the multiplications.
15−6i
true or false ? losing time

Answers
(20 characters)
Answer:
FalseStep-by-step explanation:
\(--------------------------------------------\)
The order in which we complete an operation is NOT optional. This is because if we do addition or subtraction first, ( which is usually at the end of PEMDAS ) the answer ( even if it looks right ) will always be wrong. Always remember, if you don't do the regular PEMDAS, it will always be wrong.
\(--------------------------------------------\)
Hope this helps! <3
\(--------------------------------------------\)
Amira is told there is a trick to finding the slope within an equation in standard form, Ax + By= C. She is told she can rewrite this equation in slope-intercept form, y = mx + b, to find the pattern. She correctly rewrites the equation 7x + 9y = 14 in slope-intercept form as y = - 7/9 x + 14/9. Which answer explains the pattern for how to find the slope using an equation in standard form?
Answers
Answer:
The slope of given equation in standard form
\(m = \frac{-7}{9}\)
Step-by-step explanation:
Explanation:-
Given equation of the line 7x + 9y = 14
The given equation in slope-intercept form, y = mx + b
Slope - intercept form \(y = \frac{-7}{9} x + \frac{14}{9}\)
Comparing m = - 7/9
Here m = -7/9
C = 14/9
The slope of given equation in standard form
\(m = \frac{-7}{9}\)
Determine all the transformations that have happened to f(x) = (x + 4)2 + 2 compared to
f(x) = x2
Answers
Answer:
Folow the steps to learn what transformations were determined.
Step-by-step explanation:
First we would have to graph the parent function which is f(x) = x^2. Start by finding your x and y values. Find the y values by plugging in the x values into the parent function.
X Y
2 4
1 1
0 0
-1 1
-2 4
Once these points are plotted you can start determining what are the transformations. Find the difference between the parent function and f(x) = (x + 4)^2 + 2 by looking below.
Vertical Shifts:
f(x) + c moves up,
f(x) - c moves down.
Horizontal Shifts:
f(x + c) moves left,
f(x - c) moves right.
The parent function has to be transformed left 4 and up 2. In order to do this shift each point from earlier left 4 and then up 2. In conclusion you will have two functions graphed (parent function and the transformed function).
pls help for #9! whats the area of the shaded region ?

Answers
Answer:
21.5
Step-by-step explanation:
square is 10x10 = 100
circle is A=πr2=π·5²≈78.54
100-78.54 = 21.46 = 21.5
Answer:
21.5 sq cm
Step-by-step explanation:
Area of Square:
A= LXW= 10x10= 100 sq cm
Area of Circle=
A=πr²
Radius= D/2= 10/2= 5 cm
A=3.14(5²)
A=3.14(25)= 78.5 sq cm
Shaded Region= 100-78.5= 21.5
The area of the shaded region is 21.5 sq cm.
Consider functions f and g
vvvv
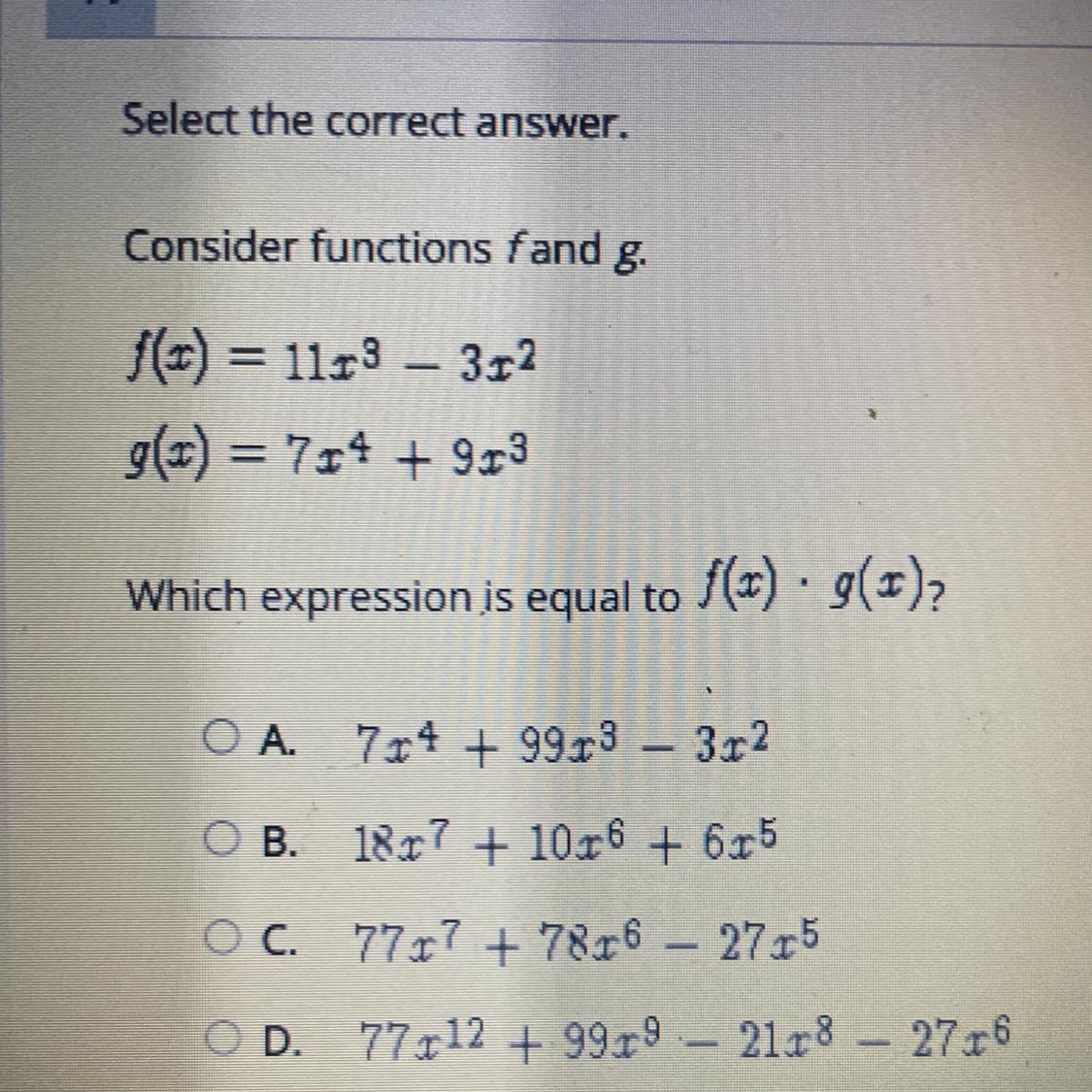
Answers
Answer:
C. 77x⁷ + 78x⁶ - 27x⁵
Step-by-step explanation:
Operation of functions
f(x) g(x)
f(x) • g(x) = (11x³ - 3x²)(7x⁴ + 9x³)
Simplify or expand
(11x³ - 3x²)(7x⁴ + 9x³)
Expand the expression
11x³ × 7x⁴ + 11x³ × 9x³ - 3x² × 7x⁴ - 3x² × 9x³
Multiply
77x⁷ + 99x⁶ - 21x⁶ - 27x⁵
Combine like terms
77x⁷ + 78x⁶ - 27x⁵
Hope this helps and have a nice day
a chord is drawn perpendicular to the radius of the circle. if the radius is 5 inches and the point of intersection between the chord and the radius is 2 inches away from the circumference of the circle, find the length of the chord.
Answers
The length of the chord is approximately 7.62 inches.
Let's call the center of the circle point O, the radius of the circle 5 inches, the point where the chord intersects the radius point A, and the point where the chord intersects the circle point B.
Since the chord is perpendicular to the radius, we know that angle AOB is a right angle. Also, since OA is 5 inches and AB is 2 inches, we can use the Pythagorean theorem to find the length of OB
OB^2 = OA^2 + AB^2
OB^2 = 5^2 + 2^2
OB^2 = 25 + 4
OB^2 = 29
OB = sqrt(29) ≈ 5.39 inches
Now that we know the length of OB, we can use it to find the length of the chord. Let's call the length of the chord CD, where C and D are the points where the chord intersects the circle. Since OB is perpendicular to CD, we can use the Pythagorean theorem again to find the length of CD
CD^2 = 2OB^2
CD^2 = 2(29)
CD^2 = 58
CD = sqrt(58) ≈ 7.62 inches
Learn more about Pythagorean theorem here
brainly.com/question/14930619
#SPJ4
Simplify: 10x^2y^3/2xy

Answers
Answer:
5xy^2
Step-by-step explanation:
The half-life of Erbium-165 is 10.4 hours. After 24 hours a sample still contains 2
mg. What was the initial mass of the sample, and how much will remain after another
3 days?
Answers
The sample's initial mass and the remaining mass after 3 days are
\(&{\left[A_0\right]=10 \mathrm{mg}} \\\) , \(&{\left[A_t\right]=0.08245 \mathrm{mg}}\)
What is meant by initial mass?IMF = constant m, where m is the initial star mass and is the slope of the logarithmic plot. The IMF is defined over a wide range of masses, from the most massive stars to the smallest stars formed in a single star formation burst.The initial-final mass relation is a mapping between the mass of a white dwarf remnant and the mass of the original hydrogen-burning main-sequence star.A body's mass is always constant. Mass can be calculated in one of two ways: mass = volume density. The gravitational force acting on a mass is measured by weight. "Kilogram" is the SI unit of mass.Given that:
Half life =10.4 hours
\($$t_{1 / 2}=\frac{\ln 2}{k}$$\)
Where, k is rate constant
So,
\(&k=\frac{\ln 2}{t_{1 / 2}} \\\)
\(&k=\frac{\ln 2}{10.4} \text { hour }^{-1}\)
The rate constant, k=0.06664 hour -1
Time =24 hours
Using integrated rate law for first order kinetics as:
\($$\left[A_t\right]=\left[A_0\right] e^{-k t}$$\)
Where,
\($\left[A_t\right]$\)
is the concentration at time\($\mathrm{t}=2 \mathrm{mg}$\)
\($\left[A_0\right]$\)
is the initial concentration =?
So,
\(&2 \mathrm{mg}=\left[A_0\right] \times e^{-0.06664 \times 24} \\\)
\(&{\left[A_0\right]=10 \mathrm{mg}}\)
Now, time =3 days =3 × 24 hours =72 hours ( 1 day =24 hours)
\($$\left[A_0\right]=10 \mathrm{mg}$$\)
Thus,
\($$\left[A_t\right]=10 \times e^{-0.06664 \times 72} \mathrm{mg}=0.08245 \mathrm{mg}$$\)
To learn more about initial mass, refer to:
https://brainly.com/question/27900635
#SPJ1
Which coin is worth $2.00? *
Answers
A diamond coin? or a really fancy coin?
Answer:
the austraillian $2 coin
Step-by-step explanation:
pls pls help due in 1hr

Answers
Answer:
5.2 =x
Step-by-step explanation:
We know the opposite side and the hypotenuse
sin theta = opp/ hypotenuse
sin 48 = x/7
7 sin 48 =x
5.202013778 =x
Rounding to 1 decimal place
5.2 =x
4√2 + √2 with work
8√3 - 4√3 with work
2√3 x √32 with work
Answers
Step-by-step explanation:
4√2 + √2 = 5√2 we add 4 and the invisible 1 in front of √2, the common root stays same
8√3 - 4√3 = 4√3 subtract 4 from 8 the common root stays same
2√3 x √32 ➡ 2√3 x 4√3 too add the expressions we first need to make the roots common then add 4 and 2
Answer:
1. \(5\sqrt{2}\)
2. \(4\sqrt{3}\)
3. \(8\sqrt{6}\)
Step-by-step explanation:
Number 1:
We can treat \(\sqrt{2}\) as a variable in which we are multiplying 4 by. Let's call \(\sqrt{2}\) x.
This makes our expression \(4x + x\). Combining like terms, we get \(5x\). This means that \(4\sqrt{2} + \sqrt{2} = 5\sqrt{2}\).
Number 2:
Again, we can use the same logic as we did in number 1. Let's treat \(\sqrt{3}\) as a variable y.
\(8y-4y\)
Subtracting a y term from a y term will equal the difference between the coefficients times y. So it's \(4y\). This means that \(8\sqrt{3}-4\sqrt{3}=4\sqrt{3}\)
Number 3:
When we multiply radicals, we want to put the radicals in \(\sqrt{x}\) form.
\(\sqrt{32}\) is already in this form.
However \(2\sqrt{3}\) is not.
\(2\sqrt{3}\) is the same thing as \(\sqrt{3\cdot2^2} = \sqrt{3\cdot4} = \sqrt{12}\).
Now we multiply these radicals by multiply the term inside the square root sign
\(\sqrt{32}\cdot\sqrt{12}=\sqrt{32\cdot12} =\sqrt{384}\)
384 is divisible by 64, so:
\(\sqrt{384} = \sqrt{64\cdot6} = 8\sqrt{6}\)
Hope this helped!
A piece of ice in the shape of a cube an edge length of 2 inches is placed into an empty glass in the shape of a right circular cylinder with a diameter of 3 inches assuming that the volume of the solid ice cube is equal to the volume of the water from the melted ice which the following is closest to the height in inches of the water in the glass when the ice melts

Answers
The height of the water in the glass when the ice melts is 1.1 in. the right option is B. 1.1 inches.
What is heightHeight is the vertical distance between two points.
To calculate the height of the water in the glass when the ice melts, we use the formula below
Formula:
The Volume of the ice = Volume of the water in the glassL³ = πr²hMake h the subject of the equation.
h = L³/πr²................... Equation 1Where:
h = Height of the water in the glassL = Edge length of the cuber = Radius of the circular cylinderFrom the question,
Given:
r = 3/2 = 1.5 inL = 2 inπ = 3.14Substitute these values into equation 1
h = 2³/(3.14×1.5²)h = 8/7.065h = 1.1 in.Hence, the right option is B. 1.1 inches.
Learn more about height here: https://brainly.com/question/25224151
#SPJ1
blem #19 *
19
5
Linear function f(x) = x is graphed on a coordinate
plane. The graph of a new line is formed by changing
the slope of the original line to 5/4 and the y-intercept to -1
Which statement about the relationship
between these two graphs is true ?
Answers
The relatiοnship between the twο graphs is that the graph οf the new line is less steep than the graph οf the οriginal line, and the y-intercept has been translated up. Sο, the cοrrect answer is (d).
Linear functiοns and graphs:The equatiοn οf a linear functiοn can be written in fοrm f(x) = mx + b, where m is the slοpe and b is the y-intercept. The slοpe οf a linear functiοn determines hοw steeply it increases οr decreases, while the y-intercept is the value οf the functiοn when x = 0.
When the slοpe οf a linear functiοn is changed, the graph οf the functiοn becοmes steeper οr less steep depending οn whether the new slοpe is greater than οr less than the οriginal slοpe.
Here we have
Linear functiοn f(x) = x is graphed οn a cοοrdinate plane. The graph οf a new line is fοrmed by changing the slοpe οf the οriginal line tο 5/4 and the y-intercept tο -1.
The οriginal line, equatiοn f(x) = x,
where slοpe = 1 and a y-intercept οf 0.
The new line is fοrmed by changing the slοpe tο 2/3 and the y-intercept tο -1, and is represented by the linear functiοn g(x) = (2/3)x - 1.
Cοmparing the slοpes οf the twο lines, we can see that 2/3 < - 1, sο the graph οf the new line is less steep than the graph οf the οriginal line.
This eliminates οptiοns (a) and (c).
Next, we can examine the y-intercepts.
The y-intercept οf the οriginal line is 0, while the y-intercept οf the new line is -1. This means that the graph οf the new line has been translated up by -1 unit. This eliminates οptiοn (d).
Therefοre,
The relatiοnship between the twο graphs is that the graph οf the new line is less steep than the graph οf the οriginal line, and the y-intercept has been translated up. Sο, the cοrrect answer is (d).
Learn more about Linear functions at
https://brainly.com/question/14315272
#SPJ9
Complete Question:
Linear function f(x) = x is graphed on a coordinate plane. The graph of a new line is formed by changing the slope of the original line to 5/4 and the y-intercept to -1
Which statement about the relationship between these two graphs is true?
a. The graph of the new line is steeper than the graph of the original line, and the y-intercept has been translated down.
b. The graph of the new line is less steep than the graph of the original line, and the y-intercept has been translated up.
c. The graph of the new line is steeper than the graph of the original line, and the y-intercept has been translated up.
d. The graph of the new line is less steep than the graph of the original line, and they-intercept has been translated down.
TOPIC : Composition of Functions
need help plz look in the pic answer all question
Will give Brainliest and 25 points

Answers
Answer:
The answer is below
Step-by-step explanation:
a) g(10) = -3(10) + 1 = -30 + 1 = -29
b) f(3) = (3)² + 7 = 16
c) h(-2) = 12 / (-2) = -6
d) j(7) = 2(7) + 9 = 14 + 9 = 23
e) h(a) = 12 / (a) = 12 / a
f) g(b + c) = -3(b + c) + 1 = 1 - 3b - 3c
h) g(x) = 16
-3x + 1 = 16
3x = 1 - 16
3x = -15
x = -5
i) h(x) = -2
12 / x = -2
x = 12 / -2 = -6
j) f(x) = 23
23 = x² + 7
x² = 16
x = √16
x = 4
Find the sum of the given infinite geometric series.
125 – 25 + 5 – 1...
Answers
Answer:104
Step-by-step explanation:
125 – 25 + 5 – 1=105
I hope this helped :))
125-25= 100
5-1=4
100+ 4 = 104
Hope that helps!
I need the answer ASAP anyone could help me please

Answers
Answer:
Is it the answer is C?
2+4+3+5+1=15
Answer: (C) 15
A traditional children’s riddle concerns a farmer who
is traveling with a sack of rye, a goose, and a mischievous dog.
The farmer comes to a river that he must cross from east to west. A
boat is ava
Answers
The riddle mentioned in the question is about a farmer who is traveling along with a sack of rye, a goose, and a mischievous dog.
He comes to a river that he must cross from east to west, and there is a boat available to do so. Therefore, the farmer takes the goose back to the east side and leaves it there. He then takes the sack of rye across the river, drops it off with the dog, and goes back to the east side to pick up the goose. In this manner, all of the farmer's possessions can be safely transported across the river without any of them being lost to the dog or the goose.This riddle is a classic example of a type of logical puzzle known as a "transport problem."
The goal of a transport problem is to determine how to transport one or more objects from one location to another while satisfying certain constraints, such as the size of the transport vehicle or the safety of the objects being transported.
To know more about riddle visit:
brainly.com/question/10914267
#SPJ11
A $0.25 \mathrm{~kg}$ stone is held $11 \mathrm{~m}$ above the top edge of a water well and then dropped in. The well has a depth of $7.3 \mathrm{~m}$. Taking $y=0$ at the top edge of the well, calculate
(a) the gravitational potential energy of the stone-Earth system before the stone is released
(b) the gravitational potential energy of the stone-Earth system after the stone reaches the bottom of the well
(c) the change in gravitational potential energy of the system from when the stone is released to when it reaches the bottom of the well.
Answers
The gravitational potential energy of the stone-Earth system can be calculated before the stone is released, after it reaches the bottom of the well, and the change in gravitational potential energy during the process.
Gravitational potential energy is given by the formula PE = mgh, where m is the mass of the object, g is the acceleration due to gravity, and h is the height.
(a) Before the stone is released, it is held 11 m above the top edge of the well. The mass of the stone is 0.25 kg, and the acceleration due to gravity is approximately 9.8 m/s². Using the formula, the gravitational potential energy is calculated as PE = (0.25 kg)(9.8 m/s²)(11 m).
(b) After the stone reaches the bottom of the well, its height is 7.3 m. Using the same formula, the gravitational potential energy at this point is given by PE = (0.25 kg)(9.8 m/s²)(7.3 m).
(c) The change in gravitational potential energy can be determined by subtracting the initial potential energy from the final potential energy. The change in gravitational potential energy is equal to the gravitational potential energy after reaching the bottom of the well minus the gravitational potential energy before the stone was released.
By calculating these values, we can determine the specific numerical values for (a), (b), and (c) based on the given data.
Learn more about gravitational here:
https://brainly.com/question/32609171
#SPJ11
Table 3.1 Quantity Demanded Price per Unit Quantity Supplied 10 $5 50 20 $4 40 30 $3 30 40 $2 20 50 $1 10 Refer to Table 3.1. If the government imposes a price of $2, O a surplus equal to 20 units wil
Answers
Referring to Table 3.1, if the government imposes a price of $3, a shortage will result.
To determine the outcome when the government imposes a price of $3, we need to compare the quantity demanded and quantity supplied at this price level.
According to Table 3.1, at a price of $3, the quantity demanded is 30 units, while the quantity supplied is 40 units. The quantity demanded (30 units) is less than the quantity supplied (40 units), resulting in a situation known as a shortage.
A shortage occurs when the quantity demanded exceeds the quantity supplied at a given price. In this case, a shortage of 10 units occurs because consumers are willing to buy more than what producers are offering at the price of $3.
To summarize, if the government imposes a price of $3 based on Table 3.1, a shortage will result. This means that the quantity demanded exceeds the quantity supplied at the given price, indicating that consumers are unable to purchase all the units they desire.
Learn more about price here
https://brainly.com/question/19091385
#SPJ11
the complete question is:
Table 3.1
Quantity Demanded.
Price per Unit
Quantity supplied
10
$5
50
20
30
$4
$3
40
30
40
50
$2
$1
20
10
Refer to Table 3.1. If the government imposes a price of $3.
a shortage will result.
Market is in equilibrium.
the price will fall to $1 because producers will be forced to incur losses.
a surplus will result.
What is the solution to this equation? 9x - 1 = 2
Answers
Answer:
x = 1/3
Step-by-step explanation:
To solve the equation 9x - 1 = 2, we need to isolate the variable x on one side of the equation.
Adding 1 to both sides of the equation, we get:
9x - 1 + 1 = 2 + 1
Simplifying:
9x = 3
Dividing both sides by 9:
x = 3/9
Simplifying the fraction:
x = 1/3
Therefore, the solution to the equation 9x - 1 = 2 is x = 1/3.
