Answers
You can see the curve is at 5
Related Questions
What percent of 2 is 32? If necessary, round your answer to the nearest tenth.
Answers
Answer:
Below
Step-by-step explanation:
32/2 x 100% = 1600 %
Read instructions and do this on a separate piece of paper and draw all lines with a ruler or any straightedge. I will mark you brainliest.

Answers
The required angles (corresponding, vertical and alternate) in relation to the Parallel lines are attached accordingly.
What is a parallel line?Parallel lines are coplanar infinite straight lines that do not cross at any point in geometry. Parallel planes are planes that never intersect in the same three-dimensional space.
When two parallel lines cross by any other line (i.e. the transversal), corresponding angles are generated in matching corners or corresponding corners with the transversal.
When two parallel lines are sliced by a transversal, the resulting alternate exterior angles are congruent, according to the Alternate Exterior Angles Theorem.
Learn more about vertical angles at:
https://brainly.com/question/24566704
#SPJ1

Halla la longitud de la hipotenusa de un triángulo si sus catetos miden
10 pies y 13 pies de largo respectivamente. Redondea tu respuesta a
dos lugares decimales.
Answers
The length of the hypotenuse is √269
The Pythagorean theorem states that the sum of the squares on the legs of a right triangle equals the square on the hypotenuse.
Given that the measures of the triangle are 10 feet and 13 feet
We have to find the length of the hypotenuse of the triangle
By Pythagoras theorem
a2 + b2 = c2
here a = 10 and b = 13
102 + 132 = c2
C2 = 100 + 169
C2 = 269
C= √269
Therefore the length of the hypotenuse is √269
To learn more about Pythagoras theorem visit
https://brainly.com/question/343682
#SPJ9
Can you please help me

Answers
Answer:
-17 (I believe)
Step-by-step explanation:
If x = 64 then the first one is asking for the square root of 64 (8)
With y being 25 the second part of this problem is actually really easy, all its doing is getting the square root and then squaring it (doing nothing at all) so that would just be 25 which would make it
8-25 which would be -17
if f={(1,3),(4,9),(5,2),(6,8)} and f(a)=8, what are all of the possible values for a?
Answers
The mean value theorem is used to link the average rate of change and the derivative of a function.
The value of V is 8.
The givenparameters are:
Mean value theorem states that:
If [a,b] and
(a,b),
Then there is a point c in (a,b), such that:
From the question, we understand that: f is differentiable
This means that:
avethat:
The equation becomes
Cross mltiply
o both side
From the question, we have:
By comparisons;
Hence, the value of V is 8.
What the meaning of statement this?

Answers
The statement is asserting that the universal class (V) is defined as the collection of all sets, where every set is included. It signifies that V encompasses all possible sets within the given set theory framework.
The statement "The universal class set, or universe, is the class of all sets: V = {x: x = x}" is referring to the concept of the universal class or the universe in set theory.
In set theory, the universal class set, denoted as V, represents the collection or class that contains all sets. It includes every possible set that can be defined or exists within the context of the set theory being considered.
The notation "{x: x = x}" is used to define the elements of the universal class. Here, "x = x" represents a condition that is always true for any object or element, regardless of its nature. In other words, this condition holds for everything in the universe, as anything is equal to itself.
Learn more about sets here:
https://brainly.com/question/30705181
#SPJ1
let x be a random variable taking values [0, 1, 2, 3] with respective probabilities [0.2, 0.5, 0.2, 0.1] (a) determine the expectation of x. (show work)
Answers
A total of 23800 cubes can fit inside the box of the given dimensions.
What is the volume of cube?The volume of a cube is given by -
Volume = a x a x a = a³
Given is that a box has a length of 10 inches, a width of 8\(\frac{3}{4}\) inches, and a height of 4\(\frac{1}{4}\) inches.
The volume of the box would be -
V = 10 x 8\(\frac{3}{4}\) x 4\(\frac{1}{4}\)
V = 10 x 35/4 x 17/4
V = 371.875 inches³
The volume of cube -
v = 1/4 x 1/4 x 1/4
v = 0.015625 inches³
Number of cubes that will fill the box would be -
n = V/v
n = 371.875/0.015625
n = 23800
Therefore, a total of 23800 cubes can fit inside the box of the given dimensions.
To solve more questions on volumes, visit the link below -
https://brainly.com/question/10498558
#SPJ1
distance between points on a coordinate plane=(y2−y1)2+(x2−x1)2−−−−−−−−−−−−−−−−−−√
Find the distance when y2=9, y1=13, x2=4,
and x1=0
.
A. 5.66
B. 5.36
C. 4.12
D. 6.95

Answers
The distance between the two points is approximately 5.66 units
A. 5.66How to find the distanceUsing the formula for the distance between two points on a coordinate plane:
Distance = √[(y2 - y1)^2 + (x2 - x1)^2]
We can plug in the given values into the distance formula:
given that
y2 = 9, y1 = 13, x2 = 4, and x1 = 0
= √[(9 - 13)^2 + (4 - 0)^2]
= √[(-4)^2 + (4)^2]
= √(16 + 16)
= √32
= 4√2
= 5.6569
= 5.66
Therefore, the distance between the two points is approximately 5.66 units, which corresponds to option A.
Learn more about coordinate plane at:
https://brainly.com/question/29765572
#SPJ1
an internet service charges 20 dollars to initiate service the companythen charges 0.50 for each day of service complete the table
Answers
Let a denote internet service charges and b denote daily service charge which are constants and x the number of days which is variable.
Let d be the number of days to find the total charges.
Since the month consists of at most 31 days
The total charges t can be expressed as t = a + b*x, where x > 0 and
x <=31.
We are given that the internet service charges of 20 dollars
We are given that the daily service charges are 0.5 dollars
The days in the month are in the range of 1 to 31 (max).
Note, if x increases by 1 unit, then t is added by b.
Given values: a = $20; b= $0.5
Solution equation:
t = $20 + x*$0.5
What is constant?
A constant is a number that stands alone; occasionally, a, b, or c are used to denote a fixed number.
What is variable?
A variable is an alphanumeric character that represents a number or a numerical value; occasionally, x, y, or z are used to denote a variable.
To know more about constant and variable check out
https://brainly.in/question/34763208
#SPJ1

Let a denote internet service charges and b denote daily service charge which are constants and x the number of days which is variable.
Let d be the number of days to find the total charges.
Since the month consists of at most 31 days
The total charges t can be expressed as t = a + b*x, where x > 0 and
x <=31.
We are given that the internet service charges of 20 dollars.
We are given that the daily service charges are 0.5 dollars.
The days in the month are in the range of 1 to 31 (max).
Note, if x increases by 1 unit, then t is added by b.
Given values: a = $20; b= $0.5.
Solution equation:
t = $20 + x*$0.5
What is constant?
A constant is a number that stands alone; occasionally, a, b, or c are used to denote a fixed number.
What is variable?
A variable is an alphanumeric character that represents a number or a numerical value; occasionally, x, y, or z are used to denote a variable.
To know more about constant and variable check out
https://brainly.in/question/34763208
#SPJ1
Consider the distribution of exam scores graded 0 from 100, for 79 students. When 37 students got an A, 24 students got a B and 18 students got a C. How many peaks would you expect for distribution?
Answers
Answer:
Three
Step-by-step explanation:
Assuming the grade score from 70 to 100 is A; for grade score from 60 to 69 is B and grade score from 50 to 59 is C. Well it is certain there are three peaks in the distribution of scores
6(x1.5)+30<48 I need help with this Help
Answers
The solution to given linear inequality, 6(x1.5) + 30 < 48, is x < 2
Solving linear inequalitiesFrom the question, we are to solve the given linear inequality
The given linear inequality is
6(x1.5) + 30 < 48
First, we will write this inequality properly.
The inequality can be properly written as
6(1.5x) + 30 < 48
Now, we will solve the linear inequality
6(1.5x) + 30 < 48
Subtract 30 from both sides of the equation
6(1.5x) + 30 - 30 < 48 - 30
6(1.5x) < 18
Divide both sides of the inequality by 6
6(1.5x)/6 < 18/6
(1.5x) < 3
1.5x < 3
Divide both sides of the inequality by 1.5
1.5x/1.5 < 3/1.5
x < 2
Hence, the solution is x < 2
Learn more on Solving linear inequalities here: https://brainly.com/question/17448505
#SPJ1
100 Points and I will mark you brainiest if right.
What is 2 x 4 x 8 x 16 x 32 x 64 divided by 2^4
Answers
Answer:
131072
Step-by-step explanation:
Let's put it into expression form and simplify as much as possible :
\(\frac{(2)(4)(8)(16)(32)(64)}{2^{4} }\) =
\(\frac{2097152}{16}\) =
131072
Hope this helped and have a good day
Answer: 131,072
Step-by-step explanation:
2 x 4=8
8 x 8=64
64 x 16=1024
1024 x 32=32768
32768 x 64=2097152
\(2^{4}\)=16
2097152/16= 131072
A population of rabbits grows exponentially at a rate of 2.1 percent per year. The population was 2600 in 1993. Step 1 of 3: Find the exponential function that represents the population r years after 1993.
Answers
The exponential function that represents the population r years after 1993 is A(t) = 2600(1.021)^t
How to find the exponential function that represents the populationFrom the question, we have the following parameters that can be used in our computation:
Initial population = 2600
Rate of growth = 2.1 percent per year
The above parameters can be represented as
Initial population, a = 2600
Rate of growth, r = 2.1% per year
The exponential function that represents the population r years after 1993 can then be represented as
A(t) = a * (1 + r)^t
Substitute the known values in the above equation, so, we have the following representation
A(t) = 2600 * (1 + 2.1%)^t
Evaluate the sum
A(t) = 2600 * (1.021)^t
So, we have
A(t) = 2600(1.021)^t
Hence, the expression is A(t) = 2600(1.021)^t
Read more about exponential function at
https://brainly.com/question/2456547
#SPJ1
Find the median of the data.
93, 81, 94, 71, 89, 92, 94,99
Find the mode(s) of the data.
Pls help
Answers
Answer:
92.5Step-by-step explanation:
The data given:
93, 81, 94, 71, 89, 92, 94, 99Put the data in the ascending order:
71, 81, 89, 92, 93, 94, 94, 99Since the data size is even, the median is the average of middle two:
median = (92 + 93)/2 = 92.5A medicine bottle contains 8 grams of medicine. One dose is 400 milligrams. How many doses does the bottle contain?
Answers
Answer:
20 doses
Step-by-step explanation:
400 milli. = 0.4 grams
8/0.4 = 20 doses
13-3p=-5(3+2p) then check equation
Answers
The answer is : p = -4
the following are the steps to solve it::
13 - 3p = -5 (3 + 2p)
calculate the area of the right hand first by multiplying the number 5 by the number in brackets
13 - 3p = -15 - 10p
move everything that contains p to the left side
13 - 3p + 10p = - 15
count all containing p
13 + 7p = -15
move the ones that don't contain p to the right
7p = -15 - 13
count on the right side
7p = - 28
p = -4
The phone company Splint has a monthly cellular plan where a customer pays a flat monthly fee and then a certain amount of money per minute used on the phone. If a customer uses 380 minutes, the monthly cost will be $173. If the customer uses 570 minutes, the monthly cost will be $249.
A) Find an equation in the form
y
=
m
x
+
b
,
where
x
is the number of monthly minutes used and
y
is the total monthly cost of the Splint plan.
Answer:
y
=
B) Use your equation to find the total monthly cost if 942 minutes are used.
Answer: If 942 minutes are used, the total cost will be
dollars.
Answers
The solution of the given problem of equation comes out to be total cost for 942 minutes is $1044.
What is an equation?The similar symbol (=) is used in arithmetic equations to signify equality between two statements. It is shown that it is possible to compare various numerical factors by applying mathematical algorithms, which have served as expressions of reality. For instance, the equal sign divides the number 12 or even the solution y + 6 = 12 into two separate variables many characters are on either side of this symbol can be calculated. Conflicting meanings for symbols are quite prevalent.
Part A:
Given:
customer uses 380 minutes, the monthly cost will be $173.customer uses 570 minutes, the monthly cost will be $249.To find an equation,
Where x is number of monthly minutes.
and y is total monthly of splint plan.
So, equation is:
\(\rightarrow \text{y} =\text{mx} +\text{b}\)
For the first case:
\(\rightarrow\bold{173 = 380x + b}\)
Second case:
\(\rightarrow\bold{249= 570x + b}\)
Solve for x:
\(\rightarrow{173 - 380\text{x}=249- 570\text{x}\)
\(\rightarrow{-207=-321\)
\(\rightarrow \text{x} =\dfrac{321}{207}\)
\(\rightarrow \text{x} =\dfrac{107}{69}\)
\(\rightarrow \text{x} \thickapprox1.55\)
For value of b
\(\rightarrow 173 = 380(1.55) + \text{b}\)
\(\rightarrow 173 - 589 = \text{b}\)
\(\rightarrow -416 = \text{b}\)
Part B:
\(\rightarrow \text{y} = 942(1.55) - 416\)
\(\rightarrow \text{y} = 1460.1 - 416\)
\(\rightarrow \text{y} \thickapprox1044\)
Therefore, the solution of the given problem of equation comes out to be total cost for 942 minutes is $1044.
To know more about the equation, visit:
https://brainly.com/question/29657983
Let's consider F(x) = x to be the parent function. Write a linear function whose graph is
shifted left 3 units, reflected over x-axis and then shifted up 5 units in this exact order.
Answers
Answer:
-3
Step-by-step explanation:
I Think :D
What is the common denominator of x+5/x+8 =1+6/x+1
Answers
Find the median weight, in kilograms (kg),
of the weights below:
14 kg, 5 kg, 16 kg,
13 kg,
17 kg,
5 kg
Answers
Answer:
See below
Step-by-step explanation:
Median is the number in the middle of a list....if there are two numbers in the middle average them
5 5 13 14 16 17 <=====average of 13 and 14 is 13.5 kg
Explain the difference between an indefinite integral and a definite integral.
A) An indefinite integral, after evaluating it at the limits of integration, results in a particular number. A definite integral results in a set of functions that share the same derivative and uses an arbitrary constant of integration.
B) A definite integral, after evaluating it at the limits of integration, results in a particular number. An indefinite integral results in a set of functions that share the same derivative and uses an arbitrary constant of integration.
C) An indefinte integral cannot always be integrated analytically and may require numeric integration, while it is always possible to integrate a definite integral. Definite integrals always return a real number after evaluation at its limits of integration.
D) A definite integral is defined and continuous over the interval of integration and has finite limits of integration. An indefinite integral is also defined and continuous over the interval of integration, but may have as a limit of integration.
Answers
The answer is A.
An indefinite integral is a function that, when differentiated, equals the original function. It is denoted by ∫f(x)dx, where f(x) is the function to be integrated. An indefinite integral always has an arbitrary constant of integration, which is denoted by C. This is because the derivative of any constant is zero, so the derivative of ∫f(x)dx+C is still equal to f(x).
A definite integral is the limit of a Riemann sum as the number of terms tends to infinity. It is denoted by ∫
a
b
f(x)dx, where a and b are the limits of integration. A definite integral does not have an arbitrary constant of integration, because the limits of integration specify a unique value for the integral.
In other words, an indefinite integral is a family of functions that share the same derivative, while a definite integral is a single number.
Determine the value of a if f(x) =(ax²-1 if x < 1 a(x² - 2x + 1) ifx>1 is continuous atx = 1.
Answers
-1 does not equal 0, the equation is not true for any value of "a". This means that there is no value of "a" for which the function f(x) is continuous at x = 1.
To determine the value of "a" for which the function f(x) is continuous at x = 1, we need to check if the left-hand limit and the right-hand limit of f(x) as x approaches 1 are equal, and if the value of f(x) at x = 1 is equal to these limits.
First, let's calculate the left-hand limit of f(x) as x approaches 1. For x < 1, the function is given by f(x) = (ax² - 1). To find the left-hand limit, we substitute x = 1 into this expression:
lim(x→1-) f(x) = lim(x→1-) (ax² - 1) = a(1²) - 1 = a - 1.
Next, let's calculate the right-hand limit of f(x) as x approaches 1. For x > 1, the function is given by f(x) = (a(x² - 2x + 1)). Substituting x = 1 into this expression, we have:
lim(x→1+) f(x) = lim(x→1+) (a(x² - 2x + 1)) = a(1² - 2(1) + 1) = a(1 - 2 + 1) = a.
For the function f(x) to be continuous at x = 1, the left-hand limit and the right-hand limit should be equal. Therefore, we have:
a - 1 = a.
To solve this equation for "a," we subtract "a" from both sides:
-1 = 0.
Since -1 does not equal 0, the equation is not true for any value of "a". This means that there is no value of "a" for which the function f(x) is continuous at x = 1.
for such more question on equation
https://brainly.com/question/17482667
#SPJ8
You may use a calculator on this question. Jesse sewed of a pair of jeans in 1. hours. How long will it take Jesse to sew of a pair of jeans? Answer as a mixed number in simplest form.

Answers
It will take 3 3/4 hours to sew 1/2 of a jean pair
Here, we want to get the amount of time it will take to sew 1/2 of a pair of jean
To answer this, we shall use the direct relation system
We have this as follows;
\(\begin{gathered} \frac{1}{5}\text{ pair= 1}\frac{1}{2}\text{ hours} \\ \\ \frac{1}{2}\text{ pair = x hours} \\ \\ \\ x\text{ }\times\text{ }\frac{1}{5}\text{ = }\frac{1}{2}\times\text{ 1}\frac{1}{2} \\ \\ \frac{x}{5}\text{ = }\frac{1}{2}\text{ }\times\text{ }\frac{3}{2} \\ \\ x\text{ = }\frac{5\times3}{2\times2} \\ \\ x\text{ = }\frac{15}{4} \\ \\ x\text{ = 3}\frac{3}{4}\text{ hours} \end{gathered}\)
HELP PLEASE I DO NOT UNDERSTAND

Answers
Answer:
A. The ordered pair (1,2) is a solution to the system of linear equations.
B. When (1,2) is substituted into the second equation, the equation is true
C. When (1,2) is substituted into the first equation, the equation is true
Step-by-step explanation:
X and Y coordinates is an address, which helps to locate a point in two-dimensional space. Any point in the coordinate plane is referred by a point (x, y), where the x value is the position of the point with reference to the x-axis, and the y value is the position of the point with reference to the y-axis. The x and y coordinates of a point have positive or negative values, based on the location of the point in the different quadrants.
so know that we know that the point (1,2) is the same as saying (x,y)
so now we just substitute both of the equation with the x and y values
x = 1
y = 2
y = -2x + 4, changes to 2 = -2(1) + 4
and
7x - 2y = 3, changes to 7(1) - 2(2) = 3
now lets solve them
Let's solve the first equation
2=(−2)(1)+4
Step 1: Multiply -2 by 1
2 = -2 + 4
Step 2: Add 4 to -2
2 = 2
Since 2 = 2, we know that (1,2) is true for this equation
Now lets solve the other, to see if it's true too
7(1) - 2(2) = 3
Step 1: Multiply 7 times 1, and -2 times 2
7 - 4 = 3
Step 2: Subtract
3 = 3
We know that (1,2) is true for this equation too
If you want to solve by substitution or elimination, you can do that too
So the answers are A, B, and C or option 1, 2, 3
−64 = −0.8k
k = ?
Please help me!!!
Answers
Answer:
Step-by-step explanation:
-64 = - 0.8k
k = -64 / -0.8
therefore k = 80
Hope it will help :)
Answer:
k = 80
Step-by-step explanation:
\( - 64 = - 0.8k\)
We can convert the decimal from - 0.8 into - 8/10.
\( - 0.8 = - \frac{8}{10} \)
Rewrite the equation.
\( - 64 = - \frac{8}{10} k\)
Move 10 to multiply - 64
\( - 64 \times 10 = - 8k \\ - 640 = - 8k\)
Then we move - 8 to divide - 640.
\( \frac{ - 640}{ - 8} = k \\ 80 = k\)
Dividing both negative equal positive. Therefore, the value of k is 80.
Answer Check
Substitute k = 80 in the equation.
\( - 64 = - 0.8 \times 80 \\ - 64 = - \frac{8}{10} \times 80 \\ - 64 = - 8 \times 8 \\ - 64 = - 64\)
The equation is true. Therefore, 80 is the right answer.
The following table (Table C2.1) is a partial listing of the sales transactions for the Watson Distributing Company for the year ended December 31, 200X. Select the first three sample items from the population using the following techniques. a. The systematic selection technique with a random starting point of 13 and a sampling interval of 30. b. The probability-proportional-to-size sampling selection technique with a random starting dollar of $17,240 and a sampling interval of $220,000. c. The random-number table selection technique using Figure 2.1 on pp. 24-25. Using the last four digits of the invoice number, begin at row (0004) and column (01), continuing across the row and then down to the beginning of the next row.
Answers
The three methods are used to select a sample from a larger population in order to make inferences about the population as a whole.
Probability-proportional-to-size sampling is a method where the probability of an item being selected is proportional to its size. In this case, the size is represented by the dollar amount of the sale.
Systematic selection involves selecting items at regular intervals. In this case, the starting point is 13 and the interval is 30. Every 30th item is selected, starting from the 13th item.
The starting dollar is $17,240 and the interval is $220,000. Every item with a sales amount that falls within the interval is selected with a probability proportional to its size.
The random-number table selection technique involves using a random number table to select items. The last four digits of the invoice number are used to determine which item is selected.
The selection process starts at row (0004) and column (01) and continues across the row and then down to the next row.
The probability of an item being selected in each method differs and is important in ensuring a representative sample is obtained.
To know more about Probability here.
https://brainly.com/question/11234923
#SPJ4

Question 16 of 22 -
MYA-Math-Alg1-CBT-2020-2021: Section 1
Question: 1-16
In the city of Carmen, there is a drawbridge that is opened twice per hour over the summer. The graph below shows the number of feet that the top of the bridge w
minutes that the drawbridge was open.
40
30
Feet Above Water
20
10
+
1
2
3
4
Minutes
The city's engineer noticed that the bridge is not opening and closing at the same rate and wanted to determine the rate of change over these intervals. Complete th
drawbridge (in feet per minute) at each of the specified intervals.
-25 -12.5-5 -2.50 2.5 5 12.5 25
Answers
Answer:
25, 0, -12.5
Step-by-step explanation:
See attached
Rate of change is:
Interval 0 - 1 min
(40-15)/(1-0) = 25/1 = 25Interval 1 - 2 min
(40 - 40)/(2-1) = 0/1 = 0Interval 2- 5 min
(15 - 40)/(4-2) = -25/2 = -12.5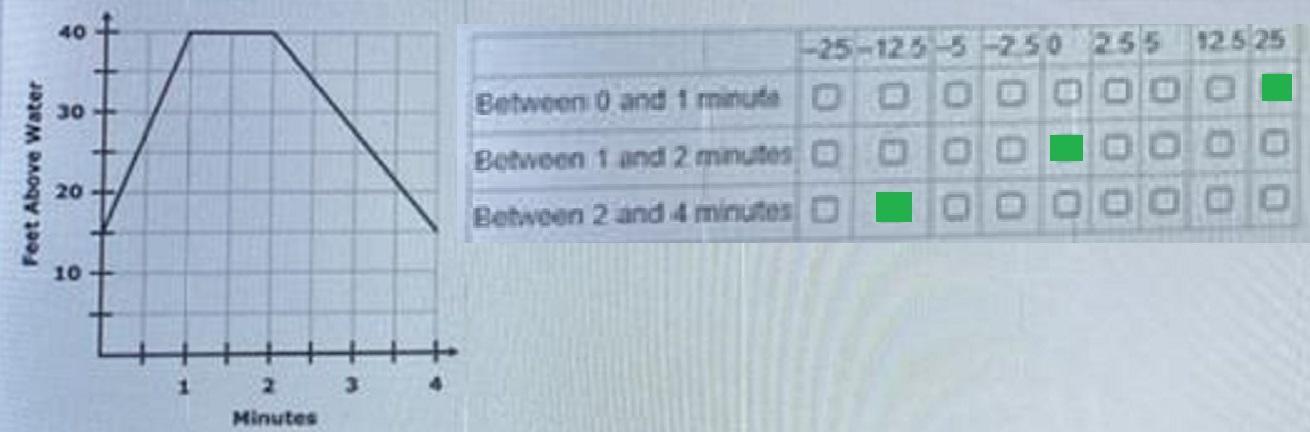
Hoang has worked as a nurse at Springfield General Hospital for 5 years longer than her friend Bill. Two years ago, she had been at the hospital for twice as long. How long has each been at the hospital?
Answers
5 years longer then Bill, 2x5=10.
10+2=12.
12-5=7
Hoang has be there for 12 years. Bill has for 7 years.
Precalculus.
Which one of these a whole number?
55
\(\sqrt{3}\)
0.3
\(\frac{1}{4}\)
Do answer.
Answers
Answer:
55
Step-by-step explanation:
Since whole numbers do not include fractions and decimal values, 55 is the answer
What is the range of f(x) = -2x + 5 with domain {1, 2, 3, 4}?
O A. {3, 1, -1, -3}
O
B. {7, 9, 11, 13}
O C. {1, 2, 3, 4}
O D. {-7.-9, -11, -13}

Answers
Step-by-step explanation:
A IS THEM ANSWER
