Answers
Related Questions
chris has been given a list of bands and asked to place a vote. his vote must have the names of his favorite and second favorite bands from the list. how many different votes are possible?
Answers
There are nC2 different votes possible, where n is the number of bands on the list and nC2 represents the number of ways to choose 2 bands out of n.
To calculate nC2, we can use the formula for combinations, which is given by n! / (2! * (n-2)!), where ! represents factorial.
Let's say there are m bands on the list. The number of ways to choose 2 bands out of m can be calculated as m! / (2! * (m-2)!). Simplifying this expression further, we get m * (m-1) / 2.
Therefore, the number of different votes possible is m * (m-1) / 2.
In the given scenario, we don't have the specific number of bands on the list, so we cannot provide an exact number of different votes. However, you can calculate it by substituting the appropriate value of m into the formula m * (m-1) / 2.
Know more about factorialhere:
https://brainly.com/question/18270920
#SPJ11
Multiply Rational Numbers Which story problem could be solved using the given equation?
\( \frac{1}{5} \times \frac{2}{3} = m\)
Answers
x2 + 4x - 5 3. Let f(x) = 23 +7.22 +19.c + 13 Note that 3 + 7.22 +19% +13 = (x + 1)(x2 +6.2 +13). (a) (4 points) Find all vertical asymptotes to the graph of f. (b) (12 points) Find the partial fracti
Answers
The partial fraction decomposition of (x^2 + 4x - 5)/(x - 1)(x + 5) is: (x^2 + 4x - 5)/(x - 1)(x + 5) = 2/(x - 1) - 1/(x + 5).
(a) Find all vertical asymptotes to the graph of f: Vertical asymptotes occur when the denominator of a rational function becomes zero. However, in the case of a quadratic equation, there are no vertical asymptotes because it does not involve a rational function. Therefore, the quadratic equation x^2 + 4x - 5 = 0 does not have any vertical asymptotes.
(b) Find the partial fraction decomposition: To find the partial fraction decomposition, we first need to factor the quadratic equation x^2 + 4x - 5 = 0. The factored form is: (x - 1)(x + 5) = 0. Now, we can write the partial fraction decomposition as: (x^2 + 4x - 5)/(x - 1)(x + 5) = A/(x - 1) + B/(x + 5)
To determine the values of A and B, we can multiply both sides of the equation by (x - 1)(x + 5) and equate the numerators: x^2 + 4x - 5 = A(x + 5) + B(x - 1). Expanding the right side: x^2 + 4x - 5 = (A + B)x + (5A - B). Equating the coefficients of like terms: A + B = 1 (coefficient of x^1), 5A - B = -5 (coefficient of x^0). Solving these simultaneous equations, we find: A = 2, B = -1. Therefore, the partial fraction decomposition of (x^2 + 4x - 5)/(x - 1)(x + 5) is: (x^2 + 4x - 5)/(x - 1)(x + 5) = 2/(x - 1) - 1/(x + 5).
To learn more about asymptotes, click here: brainly.com/question/32048252
#SPJ11
A highway's path can be found using the equation 2x + 3y = 18. Use the graphs of the functions to determine the number of intersections there will be between the railroad and the highway, and explain completely. (5 points)
Part B: A turnpike's route is determined by the equation y equals one third times x squared period Prove algebraically how many intersections there will be between the railroad and the turnpike, showing all necessary work
Answers
The intersection between the roads shown algebraically are a. no intersection, b. (4, 16/3) and (-6, 12).
What is intersection?The junction of two lines is referred to as the point of intersection. The equations a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 correspondingly depict these two lines.
The standard equation of a linear line is given as:
y = mx +c
where, m is the slope of the line.
To find the slope we require two points, and the slope is given as:
m = (y2 - y1)/ (x2 - x1)
From the graph we see that the line passes through the point (0. 8) and (3, 6).
So the slope of the graph is as follows:
m = (6 - 8) / (3 - 0)
m = - 2/3
The path of the highway also has the same slope - 2/3.
Since, L1 and L2 are parallel, there are no intersections.
Part B:
The equation given is:
y = (1/3)x^2
To find the point of intersection equate the equation of the two lines as follows:
(1/3)x^2 = - 2/3 x + 8
x^2 + 2x = 24
x^2 + x + 1 = 24 + 1
(x + 1)^2 = 25
x + 1 = 5, and x -1 = 5
x = 4, and x = 6
Substituting the value of x in equation of line find the value of y:
y = 16/3 and y = 12
So, the point of intersection is (4, 16/3) and (-6, 12).
Hence, the intersection between the roads shown algebraically are a. no intersection, b. (4, 16/3) and (-6, 12).
Learn more about intersection here:
https://brainly.com/question/14217061
#SPJ1
Order each expression from least to greatest when x = 50.
Drag and drop the expressions to order them from least to greatest.
x2
1−x
5−x
5x
Answers
1-x=-49
5-x=-45
5x=250
Least to greatest:
1-x
5-x
x2
5x
The tables for f(x) and g(x) are shown below. What is the value of (f-g)(5)

Answers
Answer:
16
Step-by-step explanation:
(f - g)(5) = f(5) - g(5)
From the table
(f(5) = 29 and g(5) = 13 , thus
f(5) - g(5) = 29 - 13 = 16
The value of function (f-g)(5) will be 16.
What is a function?A statement, principle, or policy that creates the link between two variables is known as a function.
The tables for f(x) and g(x) are shown.
Then the value of (f-g)(5) will be
(f – g)(5) = f(5) – g(5)
(f – g)(5) = 29 – 13
(f – g)(5) = 16
More about the function link is given below.
https://brainly.com/question/5245372
#SPJ5
PLS PLS i need step by step please and undefined numbers to be shown please THANK YOU!

Answers
1)The expression 4x^2-16x+12/x^2-9 is undefined when the denominator, x^2-9, equals zero because division by zero is undefined.
x^2-9 equals zero when x equals 3 or x equals -3. Therefore, the expression is undefined at x = 3 and x = -3. In all other cases, the expression is defined.
2) The given expression is:
(5-2x)/(x+2) + x^2/(x^2-4) - 5
To simplify this expression, we need to first find the LCD (least common denominator) of the two fractions. The denominator of the first fraction is x+2, and the denominator of the second fraction is x^2-4, which can be factored as (x+2)(x-2). So the LCD is (x+2)(x-2). Now we can rewrite the expression with this common denominator:
[(5-2x)(x-2) + x^2(x+2) - 5(x+2)(x-2)] / [(x+2)(x-2)]
Expanding the brackets and simplifying, we get:
(-x^3 - 3x^2 - 3x + 5) / [(x+2)(x-2)]
This expression is undefined when the denominator, (x+2)(x-2), equals zero because division by zero is undefined.
(x+2)(x-2) equals zero when x equals -2 or x equals 2. Therefore, the expression is undefined at x = -2 and x = 2. In all other cases, the expression is defined.
#SPJ1
write the standard form of the complex number. 5(cos(135°) i sin(135°))
Answers
The complex number 5(cos(135°) + i sin(135°)) can be expressed in standard form as (5√2/2) - (5√2/2)i.
To find the real and imaginary parts of the complex number, we use the trigonometric form of complex numbers. The real part is given by the product of the magnitude and the cosine of the angle, while the imaginary part is the product of the magnitude and the sine of the angle.
In this case, the magnitude is 5 and the angle is 135°. Using the cosine and sine values for 135°, which are √2/2 and -√2/2 respectively, we can calculate the real and imaginary parts as follows:
Real part = 5 * (√2/2) = 5√2/2
Imaginary part = 5 * (-√2/2) = -5√2/2
Therefore, the complex number 5(cos(135°) + i sin(135°)) can be expressed in standard form as (5√2/2) - (5√2/2)i.
Note: The standard form of a complex number is written as a + bi, where a and b are real numbers.
Learn more about complex number here:
https://brainly.com/question/20566728
#SPJ11
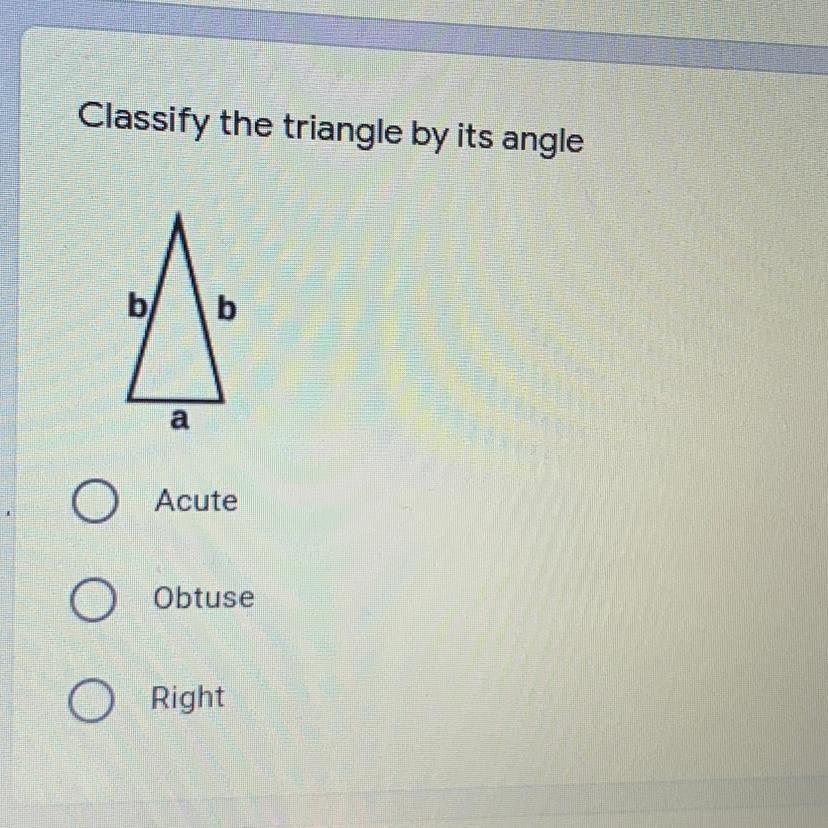
Simplify: 3a - 4 + 5a + 7 + 2(a + 1)
Answers
Answer:
10a + 5
Step-by-step explanation:
3a - 4 + 5a + 7 + 2(a + 1)
3a - 4 + 5a + 7 + 2a + 2
10a +5
Group the variables and non variables.
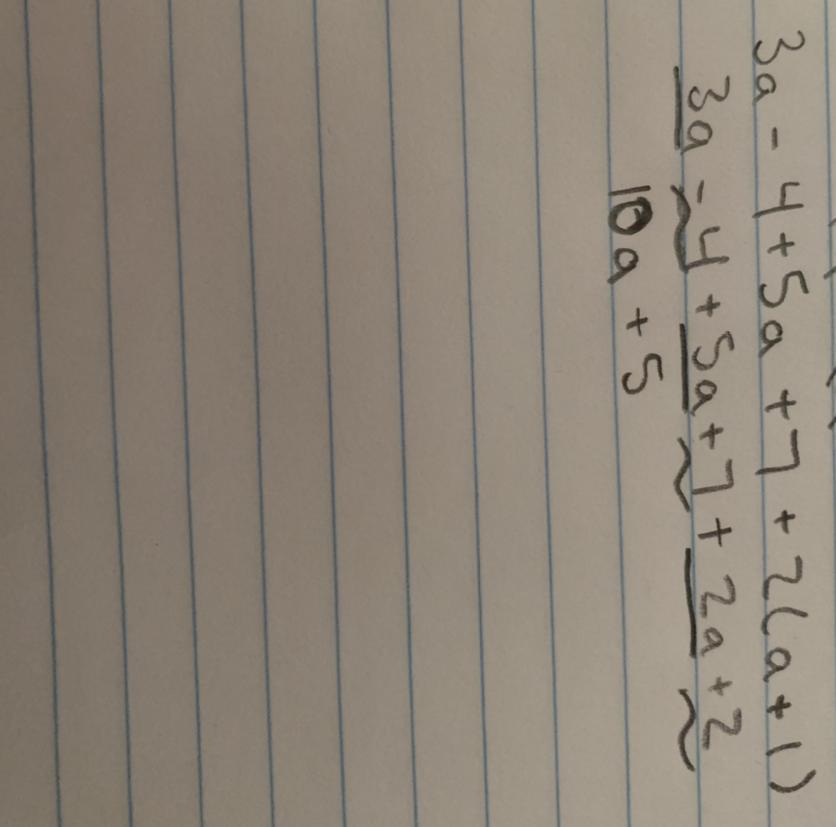
Translate into an equation, then solve: The product of a number and 14 is 28.
Answers
Answer:
x = 2
Step-by-step explanation:
Product = muliplication
Let x represent the number
14x = 28
x = 2
Consider a force which acts via the vector field defined by F = (-y, x, z). Determine the work required to move an object along the helix C defined by r(t) = (2 cos(t), 2 sin(t), ) for 0 ≤ t ≤ 2π.
Answers
the length of the helix C is 2π√5.
Now, we can calculate the work required by multiplying the constant
To determine the work required to move an object along the helix C defined by r(t) = (2cos(t), 2sin(t), z) for 0 ≤ t ≤ 2π, where the force field is defined by F = (-y, x, z), we need to evaluate the line integral of the force field along the curve C.
The line integral is given by:
∫C F · dr
where F = (-y, x, z) and dr represents the differential displacement along the curve C.
First, we need to find dr, which represents the differential displacement vector along the curve C.
dr = (dx, dy, dz)
Since r(t) = (2cos(t), 2sin(t), z), we can find dr by differentiating r(t) with respect to t:
dr = (dx, dy, dz) = (-2sin(t)dt, 2cos(t)dt, dz)
Next, we substitute F and dr into the line integral expression:
∫C F · dr = ∫C (-y, x, z) · (-2sin(t)dt, 2cos(t)dt, dz)
= ∫C (-2sin(t)(-y) + 2cos(t)x + zdz)
= ∫C (2sin(t)y + 2cos(t)x + zdz)
Now, we substitute the values of x, y, and z from the helix C:
= ∫C (2sin(t)(2sin(t)) + 2cos(t)(2cos(t)) + zdz)
= ∫C (4sin²(t) + 4cos²(t) + zdz)
= ∫C (4(sin²(t) + cos²(t)) + zdz)
= ∫C (4 + zdz)
The helix C is defined for 0 ≤ t ≤ 2π, which means the curve spans one complete revolution. Hence, the limits of integration for z are z(0) to z(2π).
Since the helix C does not specify a function for z(t), we cannot determine the limits of integration for z directly. However, if we assume that z is constant along the curve C, we can calculate the work required to move an object along the helix.
Assuming z is constant, the integral becomes:
∫C (4 + zdz) = ∫C 4 dz
= 4∫C dz
The line integral of a constant with respect to any path is simply the constant multiplied by the length of the path.
The length of the helix C can be calculated using the arc length formula:
L = ∫C ||dr|| = ∫C ||(-2sin(t)dt, 2cos(t)dt, dz)||
= ∫C √((-2sin(t))² + (2cos(t))² + (dz)²)
= ∫C √(4sin²(t) + 4cos²(t) + 1) dt
= ∫C √(4(sin²(t) + cos²(t)) + 1) dt
= ∫C √(4 + 1) dt
= ∫C √5 dt
Since the helix spans one complete revolution, the integral becomes:
L = ∫C √5 dt = √5 ∫C dt = √5 (t2π - t0) = √5 (2π - 0) = 2π√5
To know more about integral visit:
brainly.com/question/31433890
#SPJ11
If X is an exponential random variable with parameter λ, and c>0, show that cX is exponential with parameter λ/c.CDF Method:Let X be a continuous random variable and let Y=g(X)be a function of that random variable, where g(X) is some function of X. Let fX(x) be the probability density function (PDF) of X and fY(y) be the PDF of Y. Recall that the cumulative distribution function (CDF) of X is defined as the probability that X is less than or equal to some value x, for any real value of x. Mathematically,FX(x)=P(X≤x)Similarly, FY(y)=P(Y≤y).To find the distribution of Y, we can use the CDF method. We start by expressing the CDF of Y (FY(y)) in terms of X. We do this by using the fact that Y=g(X)and then solving the resulting inequality for X. Mathematically,FY(y)=P(Y≤y)=P(g(X)≤y)=⋯=P(X ???⋯)We isolate X in the inequality and we get an inequality which can be changed into CDF terms (the CDF of X).After we find the CDF of Y, we can differentiate it to get the PDF of Y. Recall that for any random variable, the first derivative of its CDF is equal to its PDF. In mathematical terms,fY(y)=ddyFY(y)We do this using the CDF of Y we obtained earlier. After completing this step, you will have the PDF of Y.
Answers
We have shown that cX is exponential with parameter λ/c when X is an exponential random variable with parameter λ and c > 0.
To show that cX is exponential with parameter λ/c when X is an exponential random variable with parameter λ, and c>0, we will use the CDF method:
1. Define the transformation: Let Y = cX be a function of the random variable X, where c > 0.
2. Find the CDF of Y: We want to find P(Y ≤ y), which is equal to P(cX ≤ y) or P(X ≤ y/c).
3. Express CDF of Y in terms of X: Since P(X ≤ y/c) is the CDF of X at y/c, we have FY(y) = FX(y/c).
4. Find the PDF of X: The exponential distribution has the PDF fX(x) = λ * exp(-λx) for x ≥ 0.
5. Differentiate the CDF of Y to find its PDF: To find fY(y), we differentiate FY(y) with respect to y. Using the chain rule, we have:
fY(y) = d(FX(y/c))/dy = fX(y/c) * (1/c)
6. Substitute the PDF of X: Now, we replace fX(y/c) with its exponential form λ * exp(-λ(y/c)):
fY(y) = (λ * exp(-λ(y/c))) * (1/c)
7. Simplify the expression: fY(y) = (λ/c) * exp(-λ(y/c))
This is the PDF of an exponential distribution with parameter λ/c. Therefore, cX is exponential with parameter λ/c when X is an exponential random variable with parameter λ and c > 0.
Learn more about "variable": https://brainly.com/question/82796
#SPJ11
A group of friends chartered a deep-sea fishing boat out of destin, fl. the graph below represents the total cost, in dollars, of the trip as a function of the number of people going. graph the group is trying to determine what the price difference would be per passenger if 10 of them go on the trip versus if 16 of them go on the trip. what is the difference in price per passenger for a group of 16 versus a group of 10? $46.25 $36.25 $56.25 $26.25
Answers
The difference in price per passenger for a group of 16 versus a group of 10 is $26.25
What is an equation?An equation is an expression that shows the relationship between two or more number and variables.
From the graph:
The cost for a group of 16 friends is $2500, while for a group of 10 friends is $1300.
Cost per passenger for 16 friend = $2500 / 16 = $156.25
Cost per passenger for 10 friend = $1300 / 10 = $130
The difference in price = $156.25 - $130 = $26.25
The difference in price per passenger for a group of 16 versus a group of 10 is $26.25
Find out more on equation at: https://brainly.com/question/2972832
#SPJ4

Answer:
D) 26.25
Step-by-step explanation:
Got it right on edge
Which of the following describes the correct process for solving the equation 2x - 6 = 22 and
arrives at the correct solution?
A. Subtract 6 from both sides of the equation and then divide by 2. The solution is x = 7.
B. Add 6 to both sides of the equation and then divide by 2. The solution is x = 14.
C. Add 6 to both sides of the equation and then divide by 22. The solution is x = -14.
D. Divide both sides by -6 and then add 2. The solution is x = 8.
Answers
Answer:
The correct solution is B
Step-by-step explanation:
2x - 6 = 22
2x = 28
x = 14
hi
Correct answer is B
2X-6 =22
2X-6 +6 = 22 +6
2X =28
2X/2 = 28/2
X=14
Find the area of the figure.

Answers
Answer:
6600
Step-by-step explanation:
6600
Solve the following quadratic equation for all values of x in simplest form. 2 ( x+ 8 ) ^2 + 9 =29
Answers
Answer:
x = -8 + sqrt(10) and x = -8 - sqrt(10)
Step-by-step explanation:
The quadratic equation to be solved is:
2(x + 8)² + 9 = 29
First, we need to simplify the left-hand side of the equation by expanding the squared term:
2(x + 8)(x + 8) + 9 = 29
Simplifying further, we get:
2(x² + 16x + 64) + 9 = 29
Distributing the 2, we get:
2x² + 32x + 128 + 9 = 29
Combining like terms, we get:
2x² + 32x + 137 = 29
Subtracting 29 from both sides, we get:
2x² + 32x + 108 = 0
Dividing both sides by 2, we get:
x² + 16x + 54 = 0
We can solve this quadratic equation by factoring or by using the quadratic formula :
The equation presented is a quadratic equation in standard form, ax² + bx + c = 0, where a = 1, b = 16, and c = 54. To solve this equation, we can use the quadratic formula, x = (-b ± sqrt(b² - 4ac)) / 2a. Plugging in the values, we get x = (-16 ± sqrt(16² - 4(1)(54))) / 2(1) = (-16 ± sqrt(16)) / 2 or (-16 ± 2sqrt(10)) / 2. Simplifying, we get x = -8 ± sqrt(10). Therefore, the two solutions to this equation are x = -8 + sqrt(10) and x = -8 - sqrt(10).
Please help! Find the area of the shaded regions. give your answer a completely simplified exact value of the terms of pi (no approximations)

Answers
For given circle, Area of shaded region is 52π cm².
What exactly is a circle?
A circle is a kind of ellipse with zero eccentricity and two foci that are coincident. A circle is also known as the locus of points drawn at equal distances from the center. The radius of a circle is the distance from its center to its outside line. The diameter of a circle is the line that divides it into two equal sections and is equal to twice the radius.
The equation for a circle in the plane is:
(x-h)^²+ (y-k)² = r²
When the coordinate points are (x, y)
(h, k) is the coordinate of a circle's center.
where r is the circumference of a circle.
where circle area = πr²
Circle circumference=2πr
Now,
Radius of biggest circle = 8cm
radius of unshaded circle= 4cm and
radius of smaller shaded circle= 2cm
Then,
Area of shaded region= Area of biggest circle - area of white circle + area of smaller shaded circle
=π*8² - π*4² + π*2²
=64π-16π+4π
=52π cm²
hence,
Area of shaded region is 52π cm².
To know more about circle visit the link
https://brainly.com/question/11833983?referrer=searchResults
#SPJ1
calculate a 95% confidence interval for the difference in mean revenue at the box office for drama and comedy movies. let dramas be population 1 and comedies be population 2. write your answer using interval notation and round the interval endpoints to two decimal places.
Answers
A 95% confidence interval for the difference in mean revenue at the box office for drama and comedy movies is (7.44, 72.56).
We have given that,
Sample mean of peoples who like drama , x₁-bar = 190
Sample mean of peoples who like comedy,x₂-bar = 150
Sample size for darama sample, n₁ = 17
Sample size for comedy sample, n₂ = 14
Standard deviations, s₁ = 60
Standard deviations, s₂ = 30
Confidence level = 0.95 or 95%
Using Z-table , Z-score for 95% confidence level is 1.96..
We have to calculate a 95% confidence interval for the difference in mean revenue at the box office for drama and comedy movies.
It is given by following Confidence interval formula,
x₁-bar - x₂-bar ± Z ( √(s₁²/n₁ + s₂²/n₂))
= 190 - 150 ± 1.96(√(60²/17 + 30²/14))
= 40 ± 1.96(√3600/17 + 900/14))
= 40 ± 32.56
= (7.44, 72.56)
Hence, the required 95% confidence interval is
(7.44, 72.56) .
To learn more about Confidence interval, refer:
https://brainly.com/question/17212516
#SPJ4
Complete question:
A Hollywood studio believes that a movie that is considered a drama will draw a larger crowd on average than a movie that is considered a comedy. To test this theory. the studio randomy selects several movies that are classified as dramas and several movies that are classified as comedies and determines the box office revenue for. each movie. The results of the survey are as follows. Assurne that the population variances are approximately equal, Calculate a
95%
confidence interval for the difference in mean revenue at the box office for drama and comedy movies: Let dramas be Population-1 and comedies be Population 2. Write your answer using interval notation and round the interval endpoints to two decimal places

(2x^2 - 4x+1)+(5x+x^2 - 1) sum PLEASE QUICKKKKKK
Answers
What are the 6 derivative rules?
Answers
The 6 derivative rules are:
The Constant Multiple Rule.The Sum and Difference Rules.The Product Rule.The Quotient Rule.The Chain Rule.The Power Rule.What is derivative?A derivative is a financial instrument that derives its value from an underlying asset. The underlying asset could be a commodity, such as gold or oil, a currency, a bond, or an index, such as the S&P 500.
Explain constant multiple rule of derivative?The constant multiple rule of derivatives states that if f(x) = cg(x), where c is a constant, then the derivative of f(x) with respect to x is equal to c times the derivative of g(x) with respect to x. This rule can be expressed mathematically as:
f'(x) = cg'(x)
To know more about rule of derivative visit:
https://brainly.com/question/25324584
#SPJ4
Lee Jenkins worked the following hours as a manager for a local Pizza Hut 5 4/1,9 4/3,7 4/3 and 8 4/3. How many total hours did Lee work?
Answers
Lee Jenkins worked the following hours as a manager for a local Pizza Hut 5 4/1, 9 4/3, 7 4/3 and 8 4/3.
Now, the above-mentioned hours are not in the proper form that we are required to calculate. Therefore, we need to change them into the proper format .In order to add these hours, we must first convert the hours and minutes to the same format.
We'll need to convert each fraction to a common denominator of 3x3=9. 5 4/1 in the mixed format is 5 + 4/1,
which is equal to 9. 9 4/3 in the mixed format is 9 + 4/3,
which is equal to 10 1/3.7 4/3 in the mixed format is 7 + 4/3,
which is equal to 8 1/3.8 4/3 in the mixed format is 8 + 4/3,
which is equal to 9 1/3.Now that we've converted the times,
we can add them together to get a total of 36 1/3 hours.
Therefore, Lee worked for 36 1/3 hours. the total number of hours Lee worked as a manager for the local Pizza Hut is 36 1/3 hours.
To know more about manager visit:-
https://brainly.com/question/32150882
#SPJ11
143 everyone please everyone answers this
Answers
y
∝
1
√
x
If
y
=
7
when
x
=
64
find,
x
when
y
=
8
b. calculate the number of grams of fe and the number of grams of co2 formed when 50.7g of fe2o3 reacts with excess co.
Answers
The balanced chemical equation for the given reaction is:Fe2O3 + 3CO → 2Fe + 3CO2The molar mass of Fe2O3 is 159.69 g/mol. Mass of Fe2O3 = 50.7 g Moles of Fe2O3 = 50.7 g / 159.69 g/mol = 0.3179 mol According to the balanced chemical equation, 1 mole of Fe2O3 reacts with 3 moles of CO.
Hence, the number of moles of CO used = 3 × 0.3179 mol = 0.9538 mol. The molar mass of CO is 28.01 g/mol. Mass of CO used = 0.9538 mol × 28.01 g/mol = 26.7 g Hence, the mass of CO2 formed will be equal to the mass of CO used, i.e., 26.7 g. The molar mass of Fe is 55.85 g/mol. Mass of Fe formed = 0.3179 mol × 2 × 55.85 g/mol = 35.27 g
The number of grams of Fe and the number of grams of CO2 formed when 50.7 g of Fe2O3 reacts with excess CO are 35.27 g and 26.7 g, respectively.
To know more about chemical equation visit:
https://brainly.com/question/28792948
#SPJ11
if a =5 b =6 and c=a-2 . answer the question , 8a-2b+1c
Answers
Answer:
here given.,
a =5 b =6 and c=a-2(5-2=3)
putting the given value in the equation...we get..
=8*5-2*6+1*3
=40-12+3
=43-12
=31
simplify this expression: 5 + 2b - 2
Answers
Combine like terms which are 5 and -2
Answer:
3 + 2b
Step-by-step explanation:
To simplify, you have to combine (add) like terms. The like terms are 5 and -2 because they both do not have a variable.
5 + (-2) = 3
2b stays the same because there are no like terms for it.
3 + 2b
Hope this helped :)
Peter compra 8 limones por $6. Cada limón tiene el mismo precio.
¿Cuál es el costo de 1 limón?
Answers
Respuesta:
Cada limón cuesta $0.75
Explicación:
$6 ➗ 8 limones = $0.75 por limon
Espero que esto ayude. Lo siento si está mal. Eres amado y eres hermoso/guapo
-Bee
Please find the equation for this parabola. Thank you!

Answers
Check the picture below.
so we know it has a vertex at (2 ,3 ) and it also passes through (-2 , -1), then
\(~~~~~~\textit{vertical parabola vertex form} \\\\ y=a(x- h)^2+ k\qquad \begin{cases} \stackrel{vertex}{(h,k)}\\\\ \stackrel{a~is~negative}{op ens~\cap}\qquad \stackrel{a~is~positive}{op ens~\cup} \end{cases} \\\\[-0.35em] ~\dotfill\\\\ \begin{cases} h=2\\ k=3\\ \end{cases}\implies y=a(~~x-2~~)^2 + 3\hspace{4em}\textit{we also know that} \begin{cases} x=-2\\ y=-1 \end{cases}\)
\(-1=a(-2-2)^2 + 3\implies -4=a(-4)^2\implies -4=16a \\\\\\ \cfrac{-4}{16}=a\implies -\cfrac{1}{4}=a\hspace{10em}\boxed{y=-\cfrac{1}{4}(x-2)^2 + 3}\)

Worth 60 points for a rapid reply- find the area of each regular polygon. Answers are rounded to the nearest whole number.

Answers
The area of the regular polygons with 12 sides(dodecagon) and 5 sides (pentagon) are 389.06 in² and 19.87 in² respectively.
How to calculate for the area of the polygonArea of regular polygon = 1/2 × apothem × perimeter
perimeter = (s)side length of octagon × (n)number of side.
apothem = s/[2tan(180/n)].
11 = s/[2tan(180/12)]
s = 11 × 2tan15
s = 5.8949
perimeter = 5.8949 × 12 = 70.7388
Area of dodecagon = 1/2 × 11 × 70.7388
Area of dodecagon = 389.0634 in²
Area of pentagon = 1/2 × 5.23 × 7.6
Area of pentagon = 19.874 in²
Therefore, the area of the regular polygons with 12 sides(dodecagon) and 5 sides (pentagon) are 389.06 in² and 19.87 in² respectively.
Read more about area here:https://brainly.com/question/27440983
#SPJ1
If y = 4 find slope, X-intercept and y-intercept.
Answers
Answer:
An equation in the form y = mx + b is in the 'slope y-intercept' form where m is the slope and b is the y-intercept. We can rewrite our equation, y = 4, in slope y-intercept form as follows: y = 0x + 4. Here, it is clear that the slope, or m, is zero. Therefore, the slope of the horizontal line y = 4 is zero
Use the example as a model. Simplify the expressions.
t^37=?
i
-i
1
-1

Answers
Answer:
Step-by-step explanation:
\((\iota)^{37}=(\iota)^{36} \times \iota=[(\iota)^2]^{18}\times \iota=(-1)^{18} \iota=\iota\)