Camila has up to $100 to spend on her birthday party at a city swimming pool.
There will be 15 friends total. She also plans to spend $38.50 on pizza.
How much can she spend per person to go to the pool?
Write an inequality to represent this situation.
Answers
x being however much she can spend on each friend
x= $12.30 if you need that too
She can spend per person to go to the pool is $ 4.1. And the inequality is 15x + 38.50 ≤ 100.
What is inequality?Inequality is simply a type of equation that does not have an equal sign in it. Inequality is defined as a statement about the relative size as we will as is used to compare two statements.
Camila has up to $100 to spend on her birthday party at a city swimming pool.
There will be 15 friends total.
She also plans to spend $38.50 on pizza.
Let, she can spend per person to go to the pool be x.
Then the amount will be
15x
If she spends $38.50 on pizza, then the equation will be
15x + 38.50
The sum of these should be less than or equal to 100. Then we have
15x + 38.50 ≤ 100
On simplifying, we have
x ≤ 4.1
More about the inequality link is given below.
https://brainly.com/question/19491153
Related Questions
Please help!
For each problem approximate the area under the curve under the given interval using five trapezoids.

Answers
Answer:
area ≈ 9.219 square units
Step-by-step explanation:
You want the approximate area under the curve y = -1/2x² +x +5 on the interval [1.5, 4] using 5 trapezoids.
Trapezoid areaThe interval can be divided into 5 intervals of width ...
(4 -1.5)/5 = 2.5/5 = 0.5
The "bases" of each trapezoid will be the function values at the ends of the intervals, for example, at x=1.5 and x=2. The "height" of each trapezoid is the width of the sub-interval, 0.5.
The area formula for a trapezoid applies:
A = 1/2(b1 +b2)h
A = 1/2(f(x) +f(x +0.5))·0.5 . . . . . for x = 1.5, 2, 2.5, 3, 3.5
Approximate total areaThe sum of the areas is computed in the attachment as ...
area under the curve = 9.21875
__
Additional comment
The value of the integral is 445/48 ≈ 9.2708333...

it is true or false?
For an exponentially distributed population Exp(0), 0>0, the mle for is given by max{X₂}
Answers
"For an exponentially distributed population Exp(0), 0>0, the mle for is given by max{X₂}" The statement is false.
The density function for an exponential distribution is given by:
f(x) = λe^(-λx) , x ≥ 0 where λ > 0 is the parameter of the distribution.
It is incorrect to say that an exponentially distributed population Exp(0) has a parameter of zero because λ must be greater than zero. When λ = 0, the density function above reduces to:
f(x) = 0, x ≥ 0
which is not a valid probability density function since the total area under the curve must be equal to one.
To estimate the parameter λ for an exponential distribution, we use the method of maximum likelihood. The likelihood function for a sample of n observations {X₁, X₂, ..., Xₙ} from an exponential distribution is given by:
L(λ) = ∏(λe^(-λxi)) = λⁿe^(-λ∑xi), i=1 to n
where ∑xi is the sum of the n observations.The log-likelihood function is given by:l(λ) = ln(L(λ)) = nln(λ) - λ∑xi
The derivative of the log-likelihood function with respect to λ is:
d/dλ l(λ) = n/λ - ∑xi
The maximum likelihood estimate (MLE) of λ is the value that maximizes the likelihood function, or equivalently, the log-likelihood function. Setting the derivative above to zero and solving for λ gives:λ = n/∑xi
which is the MLE of λ for an exponential distribution. Thus, the statement is false.
Read more about population here: https://brainly.com/question/29885712
#SPJ11
Be sure to simplify your answer.
I really need help I will give the brainiest!!

Answers
Answer:
\(h(-1)=-\dfrac{\boxed{2}}{\boxed{3}}\)
Step-by-step explanation:
Given function:
\(h(x)=\dfrac{2x-6}{4x^2+8}\)
To find h(-1), substitute x = -1 into the given function:
\(\begin{aligned}\implies h(-1)&=\dfrac{2(-1)-6}{4(-1)^2+8}\\\\&=\dfrac{-2-6}{4(1)+8}\\\\&=\dfrac{-2-6}{4+8}\\\\&=\dfrac{-8}{12}\\\\&=\dfrac{-8 \div 4}{12 \div 4}\\\\&=-\dfrac{2}{3}\end{aligned}\)
Answer:
\({ \sf{h(x) = \frac{2x - 6}{ {4x}^{2} + 8 } }} \\ \)
h(-1) implies that x = -1; therefore
\({ \sf{h( - 1) = \frac{2( - 1) - 6}{4 {( - 1)}^{2} + 8 } }} \\ \\ { \sf{h( - 1) = \frac{ - 2 - 6}{4 + 8} }} \\ \\ { \sf{h( - 1) = \frac{ - 8}{12} }} \\ \\ { \boxed{ \sf{ \: h( - 1) = - \frac{2}{3} }}}\)
Amira sells balloon animals. She uses the same number of balloons for each animal she makes. The table compares the number of balloon animals sold and the remaining number of balloons on a certain day. Animals balloons 15 200 24 164 33 128 How many balloon animals at most can’t amira sell?
Answers
Answer:
65
Step-by-step explanation:
Since we know that Amira uses 4 balloons per animal,
15 + 200/4 = 15+50 = 65
Answer:
65
Step-by-step explanation:
I just did it on Khan
When subtracting integers, the solution can be positive
true or false
Answers
Answer:
true
Step-by-step explanation:
3-2=1
-9-4=-13
Algebra:
45 + ( 84 ÷ 2 )
Answers
Answer:
The answer is 87.
Step-by-step explanation:
1) Simplify 84 ÷ 2 to 42.
\(45 + 42\)
2) Simplify.
\(87\)
Therefor, the answer is 87.
Solve for m.D:
D (9x-44)
X =
(6x+7)

Answers
Answer:
m∠D = 109
Step-by-step explanation:
This is a parallelogram.
In parallelograms, the opposite interior angles are congruent, so we can write the following equation to find, first value x the measure of m∠D:
9x - 44 = 6x + 7
Transfer like terms to the same side of the equation.9x - 6x = 7 + 44
Add/subtract.3x = 51
Divide both sides by 3x = 17
Now we can calculate measure of m∠D:
m∠D = 9x - 44
Rewrite equation using the value we found for x.9×17 + 44 = 109
Please Answer! I will give brainliest to first one that is correct

Answers
=========================================================
Explanation:
The population was 313 million and it jumped up to 324 million. This is an increase of 324-313 = 11 million
Divide this over 5, since this is the span of time from 2012 to 2017 (ie 2017-2012 = 5)
We get (11 million)/5 = 2.2 million
We basically divide 11/5 to get 2.2, then stick "million" at the end.
The average rate of change is 2.2 million people per year. This means that every year, on average, the population is going up by 2.2 million people.
------------------
Effectively, we just computed the slope through the points (2012,313) and (2017,324)
Note how using the slope formula gets us to the same result
m = slope
m = rise/run
m = (change in population)/(change in time)
m = (change in y)/(change in x)
m = (y2-y1)/(x2-x1)
m = (324-313)/(2017-2012)
m = 11/5
m = 2.2
The same idea applies if you tacked on "million" to each of the proper values mentioned.
Answer:
2,200,000 people
2.2 million
Step-by-step explanation:
You have 324 million in 2017 and 313 million in 2012
To find the average subtract the 2017 average from the 2012 average
324,000,000-313,000,000=11,000,000
That is not the average, that's the difference. To find the average, subtract the years to see how many years went by and divide 11,000,000 by that.
11,000,000/5=2,200,000
There is a 2,200,000 rate change per year
Another way would be:
324-313=11
2017-2012=5
11/5=2.2
2.2 million rate change
Hope that helps and don't be afraid to reach out with any further questions!
How do you make denominators the same when subtracting fractions?
Answers
Answer: You need to increase the terms of one or both fractions so both fractions have the same dominator
Step-by-step explanation:
A easiest way to do this is to use the "cross-multiplication"
Cross-multiplication: Cross-multiply the two fractions and create two fractions that have a common denominator
You can also search on yt a tutorial step by step
3/4 - 6/7
The denominators here are 4 & 7.
First you find the LCM (lowest common multiple) of both numbers.
Here is an easy way:
4 ---> 4, 8, 12, 16, 20, 24, 28, 32, 36, 40
7 ---> 7, 14, 21, 28, 35, 42, 49, 56, 63, 70
The least common multiple here is 28.
And so, you multiple both 7 and 4 (which are the denominators) with a number to get 28.
7*4= 28
4*7= 28
Make sure you also apply the same multiplication to the numerator.
So in conclusion:
3*7/4*7 & 6*4/7*4
I hope this helps.
taking π=22/7, find the circumference of a circle 70cm
Answers
The circumference of circle of radius 70 cm is 440 \(cm^{2}\).
According to the question,
We have the following information:
Radius of the circle = 70 cm
(Diameter is twice that of its radius..)
We know that the following formula is used to find the circumference of circle:
Circumference of circle = 2πr
(More to know: the formula to find the area of circle is π\(r^{2}\).)
(More to know: there are two values of π. One is 3.14 and one is 22/7.)
Circumference of circle = 2*(22/7)*70
Circumference of circle = 440 \(cm^{2}\)
Hence, the circumference of the circle of radius 70 cm is 440 \(cm^{2}\).
To know more about circumference here
https://brainly.com/question/4268218
#SPJ9
Find the exact values of x and y.

Answers
13 and 13√2 is the value of x and y in the given diagram
Trigonometry identityThe given diagram is a right triangle, we need to determine the value of x and y.
Using the trigonometry identity
tan45 = opposite/adjacent
tan45 = x/13
x = 13tan45
x = 13(1)
x = 13
For the value of y
sin45 = x/y
sin45 = 13/y
y = 13/sin45
y = 13√2
Hence the exact value of x and y from the figure is 13 and 13√2 respectively.
Learn more on trigonometry identity here: https://brainly.com/question/24496175
#SPJ1
Consider the function f(x,y)=2x2−4x+y2−2xy subject to the constraints x+y≥1xy≤3x,y≥0 (a) Write down the Kuhn-Tucker conditions for the minimal value of f. (b) Show that the minimal point does not have x=0.
Answers
The minimal point does not have x = 0.
(a) Kuhn-Tucker conditions for the minimal value of fThe Kuhn-Tucker conditions are a set of necessary conditions for a point x* to be a minimum of a constrained optimization problem subject to inequality constraints. These conditions provide a way to find the optimal values of x1, x2, ..., xn that maximize or minimize a function f subject to a set of constraints. Let's first write down the Lagrangian: L(x, y, λ1, λ2, λ3) = f(x, y) - λ1(x+y-1) - λ2(xy-3) - λ3x - λ4y Where λ1, λ2, λ3, and λ4 are the Kuhn-Tucker multipliers associated with the constraints. Taking partial derivatives of L with respect to x, y, λ1, λ2, λ3, and λ4 and setting them equal to 0, we get the following set of equations: 4x - 2y - λ1 - λ2y - λ3 = 0 2y - 2x - λ1 - λ2x - λ4 = 0 x + y - 1 ≤ 0 xy - 3 ≤ 0 λ1 ≥ 0 λ2 ≥ 0 λ3 ≥ 0 λ4 ≥ 0 λ1(x + y - 1) = 0 λ2(xy - 3) = 0 From the complementary slackness condition, λ1(x + y - 1) = 0 and λ2(xy - 3) = 0. This implies that either λ1 = 0 or x + y - 1 = 0, and either λ2 = 0 or xy - 3 = 0. If λ1 > 0 and λ2 > 0, then x + y - 1 = 0 and xy - 3 = 0. If λ1 > 0 and λ2 = 0, then x + y - 1 = 0. If λ1 = 0 and λ2 > 0, then xy - 3 = 0. We now consider each case separately. Case 1: λ1 > 0 and λ2 > 0From λ1(x + y - 1) = 0 and λ2(xy - 3) = 0, we have the following possibilities: x + y - 1 = 0, xy - 3 ≤ 0 (i.e., xy = 3), λ1 > 0, λ2 > 0 x + y - 1 ≤ 0, xy - 3 = 0 (i.e., x = 3/y), λ1 > 0, λ2 > 0 x + y - 1 = 0, xy - 3 = 0 (i.e., x = y = √3), λ1 > 0, λ2 > 0 We can exclude the second case because it violates the constraint x, y ≥ 0. The first and third cases satisfy all the Kuhn-Tucker conditions, and we can check that they correspond to local minima of f subject to the constraints. For the first case, we have x = y = √3/2 and f(x, y) = -1/2. For the third case, we have x = y = √3 and f(x, y) = -2. Case 2: λ1 > 0 and λ2 = 0From λ1(x + y - 1) = 0, we have x + y - 1 = 0 (because λ1 > 0). From the first Kuhn-Tucker condition, we have 4x - 2y - λ1 = λ1y. Since λ1 > 0, we can solve for y to get y = (4x - λ1)/(2 + λ1). Substituting this into the constraint x + y - 1 = 0, we get x + (4x - λ1)/(2 + λ1) - 1 = 0. Solving for x, we get x = (1 + λ1 + √(λ1^2 + 10λ1 + 1))/4. We can check that this satisfies all the Kuhn-Tucker conditions for λ1 > 0, and we can also check that it corresponds to a local minimum of f subject to the constraints. For this value of x, we have y = (4x - λ1)/(2 + λ1), and we can compute f(x, y) = -3/4 + (5λ1^2 + 4λ1 + 1)/(2(2 + λ1)^2). Case 3: λ1 = 0 and λ2 > 0From λ2(xy - 3) = 0, we have xy - 3 = 0 (because λ2 > 0). Substituting this into the constraint x + y - 1 ≥ 0, we get x + (3/x) - 1 ≥ 0. This implies that x^2 + (3 - x) - x ≥ 0, or equivalently, x^2 - x + 3 ≥ 0. The discriminant of this quadratic is negative, so it has no real roots. Therefore, there are no feasible solutions in this case. Case 4: λ1 = 0 and λ2 = 0From λ1(x + y - 1) = 0 and λ2(xy - 3) = 0, we have x + y - 1 ≤ 0 and xy - 3 ≤ 0. This implies that x, y > 0, and we can use the first and second Kuhn-Tucker conditions to get 4x - 2y = 0 2y - 2x = 0 x + y - 1 = 0 xy - 3 = 0 Solving these equations, we get x = y = √3 and f(x, y) = -2. (b) Show that the minimal point does not have x=0.To show that the minimal point does not have x=0, we need to find the optimal value of x that minimizes f subject to the constraints and show that x > 0. From the Kuhn-Tucker conditions, we know that the optimal value of x satisfies one of the following conditions: x = y = √3/2 (λ1 > 0, λ2 > 0) x = √3 (λ1 > 0, λ2 > 0) x = (1 + λ1 + √(λ1^2 + 10λ1 + 1))/4 (λ1 > 0, λ2 = 0) If x = y = √3/2, then x > 0. If x = √3, then x > 0. If x = (1 + λ1 + √(λ1^2 + 10λ1 + 1))/4, then x > 0 because λ1 ≥ 0.
To know more about constraints, visit:
https://brainly.com/question/17156848
#SPJ11
Question 8 - Select the answer that best represents the
following argument in Standard Form.
"Hard water can damage home appliances. A water softening system
can prevent hard water. Therefore, a water
Answers
Premise 1: Hard water can damage home appliances. Premise 2: A water softening system can prevent hard water. Conclusion: Therefore, a water softening system can prevent damage to home appliances.
The argument consists of two premises and a conclusion. Premise 1 states that hard water can cause damage to home appliances. Premise 2 states that a water softening system can prevent hard water. The conclusion drawn from these premises is that a water-softening system can prevent damage to home appliances.
In standard form, the argument is presented by listing the premises first, followed by the conclusion. This format helps to clearly identify the statements being made and their logical relationship. By representing the argument in this way, it becomes easier to analyze the structure and validity of the reasoning presented.
Therefore, the standard form representation of the argument is:
Premise 1: Hard water can damage home appliances.
Premise 2: A water softening system can prevent hard water.
Conclusion: Therefore, a water softening system can prevent damage to home appliances.
Learn more about Premise here:
https://brainly.com/question/30689991
#SPJ11
Simplify (62)2 what does it equal
Answers
Answer:
124
Step-by-step explanation:
62 * 2 = 124
I hope this helped! Please mark Brainliest, thank you so much!!!
Of 3,400 babies in a hospital, 1244 are boys and the rest are girls. What
percentage are girls?
Answers
9514 1404 393
Answer:
63.4% are girls
Step-by-step explanation:
The percentage that is boys is ...
1244/3400 × 100% = 36.6%
The remaining fraction is girls:
100% -36.6% = 63.4% . . . girls
f(x)= (x+1)/2
g(x)= 2x-1
Show your work to prove that the inverse of f(x) is g(x).
Show your work to evaluate g(f(x)).
Please help! I don't understand how to prove that they're inverse of eachother.
Answers
9514 1404 393
Answer:
g(f(x)) = x . . . so the functions are inverses
Step-by-step explanation:
Two functions f and g are inverses of each other if ...
g(f(x)) = x or f(g(x)) = x
We are asked to evaluate g(f(x)). That will be x if the functions are inverses.
g(f(x)) = g((x+1)/2) = 2((x +1)/2) -1 = (x +1) -1
g(f(x)) = x . . . . the functions are inverses
For which pair of triangles would you use sas to prove the congruence of the 2 triangles?.
Answers
Triangles are said to be congruent if two of their sides and the included angle are the same as their corresponding sides and angles of another triangle.
what is SAS ?When determining if a set of triangles is congruent, the Side-Angle-Side rule is utilized. According to the SAS rule, triangles are congruent if their two sides and included angles are the same as those of another triangle.
If two sides and an included angle of one triangle are equal to the sides and an included angle of the second triangle .
Then two triangles are said to be congruent according to the SAS. According to SAS theorem of congruence, two triangles are congruent if the corresponding two sides and their included angles in one triangle .
To know more about SAS visit :-
https://brainly.com/question/28035848
#SPJ4
What are the solutions to the equation x2 − 1 = 399?
Answers
Answer:
x = ±20
Step-by-step explanation:
x² - 1 = 399
x² = 400
x = ±√(400)
x = ±20
Hello !
Answer:
\(\boxed{\sf x=\pm 20}\)
Step-by-step explanation:
We want to solve the following equation :
\(x^2-1=399\)
Let's add 1 to both sides :
\(x^2-1+1=399+1\\x^2=400\)
We know that if \(x^2=a\) (assuming \(a\geq 0\)), then \(x=\pm\sqrt a\).
Let's apply this to our equation :
\(\sf x=\pm \sqrt {400}\\x=20\ \sf{or}\ x=-20\)
This equation has two solutions: x = 20 and x = -20
Have a nice day !
a right angle triangle has the perimeter of 96cm. the length of its sides are in the ratio of 6:8:10. work out the area of the triangle
Answers
Answer:
384 centimeters squared.
Step-by-step explanation:
96/(6+8+10)
96/24 = 4
6×4 : 8×4 : 10×4
24:32:40
The length of its sides are in the ratio of 24:32:40
The longest side is the hypotenuse which is 40.
The area is base × height × 1/2 of a triangle.
32 × 24 × 1/2
768 × 1/2
=384
The area of the triangle is 384 cm squared.
Answer:
Area = 384 cm²
Step-by-step explanation:
Perimeter = 96 cm
Ratio = 6:8:10
So,
6x+8x+10x = 96
=> 24x = 96
Dividing both sides by 24
=> x = 4
So, The sides are
=> 24 cm
=> 32 cm
=> 40 cm
Now the area using Heron's Formula
Area = \(\sqrt{s(s-a)(s-b)(s-c)}\)
Where s is the semi-perimeter = 48 cm, a , b and c are the sides
Area = \(\sqrt{48(48-24)(48-32)(48-40)}\)
Area = \(\sqrt{48(24)(16)(8)}\)
Area = \(\sqrt{147,456}\)
Area = 384 cm²
100 Points
3. In the image below, the m
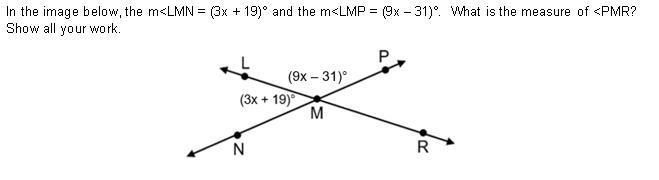
Answers
Answer:
yo can someone answere this i need it to
Step-by-step explanation:
Simplify the expression

Answers
Answer:
The answer is C i think
Step-by-step explanation:
what is the answer please.

Answers
Answer:
When x = 0 and x = 6 then function is undefined.
Step-by-step explanation:
When the denominator of the function is zero, then the function is undefined.
x² - 6x = 0
x(x - 6) = 0
x = 0 or x - 6 = 0
x = 6
When x = 0 or x = 6, the denominator will become zero.
x = 0 ⇒ x² - 6x = 0 and
x = 6 ⇒ x² - 6x = 6² - 6*6
= 36 -36
= 0
When x = 0 and x = 6 then function is undefined.
Select the correct answer from each drop-down menu. Graph of a four-sided polygon on a coordinate plane at A (minus 1, minus 1), B (0, 1), C (2, 2), and D (2, minus 1). In the figure, polygon ABCD is dilated by a factor of 2 to produce A′B′C′D′ with the origin as the center of dilation. Point A′ is at , and point D′ is at .
Answers
From (0, 0), the points A and D in the graph are at (-1, -1) and (2, -1) respectively.
How to depict the graph?Since the scale factor is 2, every point will be moved twice a distance in both directions. (x and y).
So, multiplying both coordinates by 2, we will get the dilated points.
Hence, A' will be at (2 × (-1), 2 × (-1)) = (-2, -2) and D' will be at (2 × 2, 2 × (-1)) = (4, -2).
Learn more about graph on:
https://brainly.com/question/19040584
#SPJ1

Find the equation of the line through point (4,−7) and parallel to y=−23x+32.
Answers
Answer:
y = -23x + 85
Step-by-step explanation:
for an equation to be parallel to another, they must have the same slope. So plugging in (4, -7) we get -7 = -23(4) + P. P being the new y intercept we must find. Now simple algebra add -23(4) = -92 to both sides and we get 85 = P. Plug in to y = mx + b and we get
y = -23x + 85
Huuureyyyyy pllzzzzz Which expression is equivalent to x^-5/3?

Answers
Answer:
\(\frac{1}{\sqrt[3]{x^5} }\)
Step-by-step explanation:
it's negative exponent so in order to get it positive it goes to the denominator of the fraction for positive exponent number
then the x to the exponent the numerator is the power and the denominator is the sqrt number
\(\frac{1}{\sqrt[3]{x^5} }\)
Bob's gift shop sold a record number of cards for Mother's Day. One salesman sold 46 cards, which was 10% of the cards sold for Mother's Day. How many cards were sold for Mother's Day?
Answers
The total 460 cards are sold on Mothers day.
Given that, Bob's gift shop sold a record number of cards for Mother's Day.
One salesman sold 46 cards, which was 10% of the cards sold for Mother's Day.
Let the number of cards sold on mothers day be x.
Here, 10% of x =46
10/100 ×x= 46
10x=4600
x=460
Therefore, total 460 cards are sold on Mothers day.
To learn more about the percentage visit:
brainly.com/question/24159063.
#SPJ1
235litre in cubic cm
the one who will first give answer marks as brainliest
Answers
(just multiply the volume by 1000)
Given the function h of x equals 3 times the cube root of x minus 5 end root plus 6, what is the x-intercept of the function?
Answers
The x-intercept of the function is -3
What is x-intercept?One example of an intercept is the X-intercept, which is when a line crosses the x-axis.
Where a line crosses the y-axis is known as the y-intercept.
One play in numerous football formats is the interception.
Donald Hamilton's 1980 thriller The Mona Intercept
Nixon announced Operation Intercept as a drug-prevention initiative.
Telephone monitoring, often known as third-party eavesdropping on phone and online talks
Android smartphone Samsung Intercept (SPH-M910) Visual Intercept, a Microsoft Windows-based software defect monitoring tool
A measurement of the linearity of an electrical device is the intermodulation intercept point.
A telephone recording known as the intercept message informs the caller that the call cannot be finished.
The Intercept is an online news source run by Jeremy Scahill, Laura Poitras, and Glenn Greenwald.
To learn more about x-intercept from the given link:
https://brainly.com/question/3761242
#SPJ4
Answer:
To find the x-intercept of the function, we need to find the value of x where the function h(x) is equal to zero.
Setting h(x) = 0, we have:
0 = 3∛(x - 5) + 6
Subtracting 6 from both sides, we get:
-6 = 3∛(x - 5)
Dividing both sides by 3, we get:
-2 = ∛(x - 5)
Cubing both sides, we get:
-8 = x - 5
Adding 5 to both sides, we get:
x = -3
Therefore, the x-intercept of the function is -3.
The answer is: -3.
which sampling method is being described
A store manger randomly choose a shopper entering her store to interview she then interview every 20th person after that contomer
to do the survey
Answers
Systematic sampling offers several advantages. It is relatively easy to implement and eliminates bias that may arise from the subjective selection of participants.
The sampling method described in the scenario is called systematic sampling.
Systematic sampling involves selecting every nth element from a population after randomly selecting a starting point. In this case, the store manager randomly chooses a shopper entering the store as the starting point and then proceeds to interview every 20th person after that initial selection.
Systematic sampling offers several advantages. It is relatively easy to implement and eliminates bias that may arise from the subjective selection of participants. By ensuring a regular interval between selections, systematic sampling provides a representative sample from the population.
However, it's important to note that systematic sampling can introduce a form of bias if there is any periodicity or pattern in the population. For example, if the store experiences a peak in customer traffic during specific time periods, the systematic sampling method might overrepresent or underrepresent certain groups of shoppers.
To minimize this potential bias, the store manager could randomly select the starting point for the systematic sampling at different times of the day or on different days of the week. This would help ensure a more representative sample and reduce the impact of any inherent patterns or periodicities in customer behavior.
for more such question on relatively visit
https://brainly.com/question/29502088
#SPJ8
what is happening at this step in the equation solving process for 3x+7=5x
7=2x
Answers
This is so you only have a variable on one side
-3x -3x
7=2x
(Divide both sides by 2)
x=3.5