.- Calcule el interés producido por un capital de 4 500 dólares al 5% de interés simple anual en 8 meses.
Answers
Answer: $150
Step-by-step explanation:
Hi, the question says:
Calculate the simple interest produced by $4500 at 5% simple annual interest in 8 months.
To answer this question we have to apply the simple interest formula:
I = p x r x t
Where:
I = interest
P = Principal Amount
r = Interest Rate (decimal form)
t = years
Since 1 year = 12 months;
For 8 months:
8/12 = 2/3 years
Replacing with the values given
I = 4500 x (5/100) x 2/3
I = $150
Feel free to ask for more if needed or if you did not understand something.
Related Questions
A cup has the shape of a right circular cone. The height of the cup is 12 cm, and the radius of the opening is 3 cm. Water is poured into the cup at a constant rate of 2cm3/sec What is the rate at which the water level is rising when the depth of the water in the cup is 5 cm?
Answers
Answer:
The rate at which the water level is rising when the depth of the water in the cup is 5 centimeters is approximately 0.407 centimeters per second.
Step-by-step explanation:
From Geometry, we find that the volume of the cone (\(V\)), measured in cubic centimeters, is defined by the formula:
\(V = \frac{\pi\cdot \cdor r^{2}\cdot h}{3}\) (Eq. 1)
All right circular cone satisfies the following relationship:
\(\frac{h}{r} = \frac{h_{max}}{r_{max}}\)
\(r = \left(\frac{r_{max}}{h_{max}} \right)\cdot h\) (Eq. 2)
Where:
\(r\) - Radius of the right circular cone, measured in centimeters.
\(h\) - Height of the right circular cone, measured in centimeters.
By applying (Eq. 2) in (Eq. 1), we get the following formula:
\(V = \frac{\pi}{3} \cdot \left(\frac{r_{max}}{h_{max}} \right)^{2}\cdot h^{3}\) (Eq. 1b)
Given that \(r_{max}\) and \(h_{max}\) are constant, we get the rate of change for the volume of the right circular cone (\(\dot V\)), measured in cubic centimeters per second:
\(\dot V = \pi\cdot \left(\frac{r_{max}}{h_{max}} \right)^{2}\cdot h^{2}\cdot \dot h\) (Eq. 2)
Where \(\dot h\) is the rate of change of the water level, measured in centimeters per second.
If we know that \(\dot V = 2\,\frac{cm^{3}}{s}\), \(r_{max} = 3\,cm\), \(h_{max} = 12\,cm\) and \(h = 5\,cm\), the rate of change of the water level is:
\(\dot h = \frac{\dot V}{\pi\cdot h^{2}}\cdot \left(\frac{h_{max}}{r_{max}} \right)^{2}\)
\(\dot h =\left[\frac{2\,\frac{cm^{3}}{s} }{\pi\cdot (5\,cm)^{2}}\right] \cdot \left(\frac{12\,cm}{3\,cm} \right)^{2}\)
\(\dot h \approx 0.407\,\frac{cm}{s}\)
The rate at which the water level is rising when the depth of the water in the cup is 5 centimeters is approximately 0.407 centimeters per second.
The rate at which the water level is rising when the depth of the water in the cup is 5 centimetre is approximately 0.407 centimetre per second.
Given the height h of the cup is 12 cm, and the radius r of the opening is 3 cm.
Given, A cup has the shape of a right circular cone.
We know that the volume of cone, V \(=\frac{\pi r^{2}h }{3}\).......equation 1.
here h is the height and r is the radius of the cone respectively.
All right circular cone satisfies the relationship, \(\frac{h}{r} =\frac{h_{max} }{r_{max} }\)
Now, \(r=\frac{r_{max} }{h_{max} } h\)...equation 2.
From equation 1 and equation 2, we get\(V=\frac{\pi }{3} . (\frac{r_{max} }{h_{max} }h) ^{2} .h\\\)
\(V=\frac{\pi }{3} .(\frac{r_{max} }{h_{max} } )^{2}. h^{3}\)
Given that \(r_{max}\) and \(h_{max}\) are constant, we get the rate of change for the volume of the right circular cone \(V_{1}\) , measured in cubic centimetre per second.
\(V_{1} =\pi (\frac{r_{max} }{h_{max} })^{2} h^{2} .h_{1}\) here \(h_{1}\) is the rate of change of the water level, measured in centimetres per second.
Here \(V_{1} =2cm^{3} per sec\), \(r_{max} =3\), \(h_{max}=12\) and \(h=5\) putting these values in above formulae, we get \(2 =\pi (\frac{3}{12} )^{2} .5^{2} .h_{1}\)
on calculating we get, \(h_{1} = 0.407 cm per sec\)
Hence The rate at which the water level is rising when the depth of the water in the cup is 5 centimetre is approximately 0.407 centimetres per second.
For more details on volume of cone follow the link:
https://brainly.com/question/1315822
mountains poem in nepali for class 7
Answers
Step-by-step explanation:
म नजन्मिदै विधवा भएकी हिमाल
खै! किन हो मेरा यी हेर्ने नयनले उनलाइ
अझै पनि दिन र रातमा
सेतै लुगा पहिरिएकी देख्छ
अचम्म लाग्छ मलाइ पहिरिएकी सेतो लुगा माथि
मुनालले पाइला टेके पनि विष्ठा गरे पनि कहिल्यै
मैलो हुदैन सेतो लुगाको वास्तविक रङ
उत्तिकै सेतो देख्छु म
निर्जीव वस्तु भएनी हिमाललाइ
सजीव मनुस्यको जस्तै चोटको कल्पना गरेको छु मैले
किनकी चोटै चोटले ग्रसित भएकी उनी आजभोली
अपाङ्गको सिकार बनिसकेकी छिन
उनलाइ अन्धो भन्छु म किनकी उनी आँखा देख्दैनन
आँखा नदेखे पनि अरु कसैलाइ सुम्सुम्याउन समेत सक्दैनन
तर पनि कस्तुरी, डाफे,मुनाल,घोरल,चितुवा आदि जनावरहरुको
सहारा दिने आश्रय स्थल भएर उभिएकी छिन, के कम छिन र?
जमिन भित्र उनको खुट्टा गाडिएर होला
खुट्टाको दृश्य मैले अझै पनि देख्न पाएको छैन
कस्तो होला है! हिमालको खुट्टा ? सोचिरहन्छु म
सायद खुट्टा नै छैन र पो कहिल्यै पनि हिड्डुल गर्न सक्दैनन कि?
जब कुनै समयमा चुचुरोमा हावा बहन थाल्यो
एकदिन सेतो कपाल धरतीमा हाम फालेर
नदिहरु बढ्न थाले तर उहीँ बहेको हावाले
हिमालको श्रवण गर्ने कानको जाली
नै फुटाइदिएछ त्यही भएर म भन्छु
हिमाललाइ बहिरो पनि हुनुहुन्छ तपाईं
सधै टोलाएर बसेकी देख्छु म
रोजगारी भन्ने कुरा त उहीँ हो हिमाललाइ
बिहानीपख देखि सन्ध्या काल सम्म
प्रकृतिले बसिबसी ऐना टल्काउने
पदभार ग्रहण गराइदिएको छ जब घाम
झुल्किन्छ उनी अस्ताउन्जेल सम्म ऐना टल्काइरहन्छिन्
त्यसैले म भन्छु हिमाललाइ बिधवा भएर के भो त
खान लाउनको लागि रोजगारी मिलेकै छ क्यारे !
6- A two-dimensional strain field is given by: Ex =c(-4.5x2+10.5y?) &y=c(1.5x27.5y?) Yxy =1.5bxy where b and c are nonzero constants. a) What should the relationship between b and c be if this field is to satisfy the strain compatibility conditions? b) Determine the displacements u and v corresponding to this field of strain at point (3,7) if they are zero at point(0,0). Use as a value of 2.5 for c.
Answers
a) The relationship between b and c is that c cannot be zero.
b) b can be any nonzero constant and c is equal to 2.5 in this case.
In two dimensions, the compatibility equations for strain are,0
∂εx/∂y + ∂γxy/∂x = 0
∂εy/∂x + ∂γxy/∂y = 0
where εx and εy are the normal strains in the x and y directions, respectively, and γxy is the shear strain.
Using the given strain field, we can calculate the strains,
εx = -4.5cx² + 10.5cy
εy = 1.5cx² - 7.5cy²
γxy = 1.5bxy
Taking partial derivatives and plugging them into the compatibility equations, we get,
⇒ -9cx + 0 = 0
⇒ 0 + (-15cy) = 0
These equations must be satisfied for the strain field to be compatible. From the first equation,
We get cx = 0, which means c cannot be zero.
From the second equation, we get cy = 0,
Which means b can be any nonzero constant.
For part b:
We are asked to find the displacements u and v corresponding to the given strain field at points (3, 7), assuming they are zero at point (0, 0) and using c = 2.5.
To find the displacement components,
We need to integrate the strains with respect to x and y. We get,
u = ∫∫εx dx dy = ∫(10.5cy) dy = 5.25cy²
v = ∫∫εy dx dy = ∫(1.5cx² ) dx - ∫(7.5cy²) dy = 0.5cx³ - 2.5cy³
Plugging in the values of c and b, we get,
u = 5.25(2.5)(7)² = 767.62
v = 0.5(2.5)(3)³ - 2.5(7)³ = -8583.75
Therefore,
The displacements at points (3, 7) are u = 767.62 and v = -8583.75.
To learn more about derivatives visit;
https://brainly.com/question/29144258
#SPJ4
PLS HELP
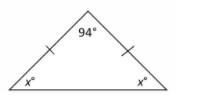
What is the value of x ?
A. 42
B. 43
C. 84
D. 86
Answers
Answer:
B
Step-by-step explanation:
x+x+94 = 180 (sum of angle of triangle)
2x+94 = 180
2x = 180-94
2x = 86
x = 86÷2
Therefore x = 43
Select the correct answer.There are 6 adult chaperones, 21 female students, and 23 male students on a bus for a field trip.What is the probability that a randomly chosen person on the bus is an adult chaperone or a male student? A- 1/2 B- 29/50C- 2/3D- 1/29a whole explanation and answer will get marked brainiest

Answers
Let A be the event that we choose an adult chaperone and let B be the event that we pick a male student. Then, we want to calculate the following probability.
\(P(A\cup B)\)where the symbol between A and B means the union of events, which could be understood as "or". Using the properties of probability, we have
\(P(A\cup B)=P(A)+P(B)-P(A\cap B)\)where the symbol on the right, between A and B, is the intersection, which can be understood as "and". Since we are going to pick only one person, it is impossible that we pick an adult chaperona and a male student. So,
\(P(A\cap B)=0\)So we have
\(P(A\cup B)=P(A)+P(B)\)Now, we want to calculate P(A) and P(B).
To calculate the probability of each event, we first count the number of possibilities that the event is true.
Note that since we have 6 adult chaperones, we have 6 possibilites such that the event A is true. Now, to calculate the probability of A, we simply divide this number by the total number of people on the bus (which is 50). So we get
\(P(A)=\frac{6}{50}\)In the same manner, for event B, we have a total of 23 possibilities such that the event B is true. Then
\(P(B)=\frac{23}{50}\)Finally, by replacing this values in the original expression, we have
\(P(A\cup B)=P(A)+(B)=\frac{6}{50}+\frac{23}{50}=\frac{29}{50}\)How to find value of x with secant and tangent
Answers
Answer:
hloa
Step-b omcetaso
(sin(\theta )+cos(\theta )-tan(\theta ))/(sec(\theta )+csc(\theta )-cot(\theta )) given that tan\theta =-(4)/(3) in quadrant II
Answers
We have to find the value of `(sinθ+cosθ−tanθ)/(secθ+cscθ−cotθ)`
Let's find all trigonometric ratios:
We can say that:
\($$\tan \theta= \frac{opp}{adj}= \frac{-4}{3}$$$$\text\)
{Using the Pythagorean Theorem we can find the hypotenuse }
\($$$$\text{Hypotenuse = } \sqrt{(-4)^2+(3)^2}\)
\(= \sqrt{16+9}\)
= \(\sqrt{25}\)
=\(5$$$$\)
Substituting the values of sinθ, cosθ and tanθ in `
\(= \frac{\frac{3}{5} + \frac{-4}{5} - \frac{-4}{3}}{\frac{-4}{5} + \frac{5}{3} - \frac{-3}{4}}$$$$\)
\(=\frac{\frac{9}{15} + \frac{-12}{15} + \frac{20}{15}}{\frac{-16}{20} + \frac{25}{12} + \frac{3}{4}}$$$$\)
\(=\frac{\frac{17}{15}}{\frac{-14}{15}}$$$$\)
\(=-\frac{17}{14}$$\)
Therefore, \(`(sinθ+cosθ−tanθ)/(secθ+cscθ−cotθ)\)` is equal to
`-17/14` when `tanθ=−43` (Quadrant II).
To know more about Pythagorean visit:
https://brainly.com/question/28032950
#SPJ11
-10b + 5 = 7b + 5 .
ANSWER ASAP
Show step by step on paper please.
Answers
Answer:
your answer should be b= 17

a cone has volume of 98cm the radius of the cone is 5.13 what is the hight of the cone
Answers
Step-by-step explanation:
v=1/3πr²h
98=1/3×22/7×(5.13)²×h
98=1/3×22/7×(27.2403)×h
98=28.537×h
h=28.537/98
h=0.291m
hope it helps. please mark brainliest
Answer:
Answer to your question is in the attachment

Look at photo for problem
Just need chart filled out

Answers
Answer:
1. x=0,y=-1
2. x=1 y=-4
3. x=2 y=-5
4. x=3 y=-4
5. x=4 y=-1
Step-by-step explanation:
\(y=x^{2} -4x-1\)
insert x
0
1
2
3
4

Write an equation of a line through the point (6, 2) with slope 2/3.
Answers
Answer:
y=2/3x-2
Step-by-step explanation:
Will Give Branliest. To decorate for a party, Rob and Loretta were each given a bag of balloons. There were 40 balloons between both bags. Rob used 8 balloons from his bag, and Loretta used 8 balloons from hers. The product of the number of balloons left in each bag is no more than 44.
Let x represent the number of balloons that Rob had in his bag before he used any. Which choice represents the number of balloons left in their bags?
A. x^2-40x=300
B. x^2-40x+300>=0
C. x^2-40x-300<0
D. x^2-40x-300=0
If Rob originally had more balloons than Loretta, what is the least number of balloons that Rob could have had before using any?
A. 10
B 20
C.30
Answers
Last one absolutely(We need quadratic equation not inequality here)
Let's check again for confirmation
\(\\ \rm\rightarrowtail x^2-40x+300=0\)
\(\\ \rm\rightarrowtail x^2-30x-10x+300=0\)
\(\\ \rm\rightarrowtail (x-30)(x-10)=0\)
\(\\ \rm\rightarrowtail x=30,10\)
X has values 30 and 10
Rob has highest means atleast 30
Answer:
B. x² - 40x + 300 ≥ 0
C. 30
Step-by-step explanation:
Let x = number of balloons Rob started with
Let y = number of balloons Loretta started with
Given:
There were 40 balloons between both bags⇒ x + y = 40
Given:
Rob used 8 balloons from his bag, and Loretta used 8 balloons from hers. The product of the number of balloons left in each bag is no more than 44.⇒ (x - 8)(y - 8) ≤ 44
Rewrite x + y = 40 to make y the subject:
⇒ y = 40 - x
Substitute into (x - 8)(y - 8) ≤ 44 and simplify:
⇒ (x - 8)(40 - x - 8) ≤ 44
⇒ (x - 8)(32 - x) ≤ 44
⇒ 32x - x² -256 + 8x ≤ 44
⇒ - x² + 40x - 256 ≤ 44
⇒ - x² + 40x - 300 ≤ 0
Dividing both sides by -1 (remembering to change the direction of the inequality sign):
⇒ x² - 40x + 300 ≥ 0
Factor x² - 40x + 300 ≥ 0
⇒ x² - 10x - 30x + 300 ≥ 0
⇒ (x² - 10x) + (-30x + 300) ≥ 0
⇒ x(x - 10) -30(x - 10) ≥ 0
⇒ (x - 10)(x -30) ≥ 0
Therefore, x ≤ 10 or x ≥ 30
As x + y = 40:
If x ≤ 10 then y ≥ 30
If x ≥ 30 then y ≤ 10
If Rob (x) had MORE balloons than Loretta (y) then only
If x ≥ 30 then y ≤ 10 is valid
Therefore, the least number of balloons Rob could have had before using any is 30.
Solve the right triangle. Round your answers to the nearest tenth.

Answers
The value of the missing parts of the given right triangle is given as follows:
A = 46°
a = 13.5
c = 18.7
How to calculate the value of the missing parts of the triangle?To determine the missing part of the triangle, the following should be carried out.
The total internal angle of a triangle = 180°
The given angle = 90°+44° + A = 180°
180° = 134°+ A
A = 180-134 = 46°
Using the sine formula;
a/sinA = b/sinB
a =?
A = 46°
b = 13
B = 44°
That is ;
a/sin 46° = 13/sin 44°
a = 0.719339800×13/0.694658370
= 13.5
Using the Pythagorean formula;
c² = a²+b²
c² = ?
a = 13.5
b = 13
c² = 13.5²+13²
= 180.9+169
= 349.9
c = √349.9
= 18.7
Learn more about triangle here:
https://brainly.com/question/28470545
#SPJ1
Number one is already done so I just need help with the rest.

Answers
We are given three points
F(4, 7)
G (5, 7)
H (5, 9)
This ordered of pairs can be represented using x and y
For point F
x = 4, and y = 7
For point G
x = 5, and y = 7
For point H
x = 5, and y = 9

Solve for x assume that lines appear tangent are tangent

Answers
Answer:
Step-by-step explanation:
? = 1/2(230)
A 115°
At a local bed and bath superstore the manager, Jill roe, knows her customers will pay no more than $250 for a bedspread. Jill wants a 30% mark ip on selling price. What is the most that Jill can pay for a bedspread
Answers
Jill can pay a maximum of $192 for a bedspread.
Jill wants to mark up the price of the bedspread by 30%, so she needs to pay at least 250 / 1.3 = $192 for it. If she pays more than $192, she will not be able to make a 30% profit.
Jill wants to mark up the price of the bedspread by 30%. This means that she wants to sell it for 1.3 times the price she pays for it.
The maximum price that customers are willing to pay is $250.
If Jill pays more than $192 for the bedspread, she will not be able to sell it for $250 and make a 30% profit.
Therefore, the most that Jill can pay for the bedspread is $192.
To learn more about profit here brainly.com/question/32381738
#SPJ11
Jill can pay a maximum of $192 for a bedspread.
Jill wants to mark up the price of the bedspread by 30%, so she needs to pay at least 250 / 1.3 = $192 for it. If she pays more than $192, she will not be able to make a 30% profit.
Jill wants to mark up the price of the bedspread by 30%. This means that she wants to sell it for 1.3 times the price she pays for it.
The maximum price that customers are willing to pay is $250.
If Jill pays more than $192 for the bedspread, she will not be able to sell it for $250 and make a 30% profit.
Therefore, the most that Jill can pay for the bedspread is $192.
To learn more about profit here brainly.com/question/32381738
#SPJ11
Find the union and the intersection of the given intervals I₁=(-2,2]; I₂=[1,5) Find the union of the given intervals. Select the correct choice below and, if necessary, fill in any answer boxes within your choice A. I₁ UI₂=(-2,5) (Type your answer in interval notation.) B. I₁ UI₂ = ø Find the intersection of the given intervals Select the correct choice below and, if necessary, fill in any answer boxes within your choice. A. I₁ ∩I₂ (Type your answer in interval notation) B. I₁ ∩I₂ = ø
Answers
To find the union and intersection of the intervals I₁ = (-2, 2] and I₂ = [1, 5), let’s consider the overlapping values and the combined range.
The union of two intervals includes all the values that belong to either interval. Taking the union of I₁ and I₂, we have:
I₁ U I₂ = (-2, 2] U [1, 5)
To find the union, we combine the intervals while considering their overlapping points:
I₁ U I₂ = (-2, 2] U [1, 5)
= (-2, 2] U [1, 5)
So the union of the intervals I₁ and I₂ is (-2, 2] U [1, 5).
Now let’s find the intersection of the intervals I₁ and I₂, which includes the values that are common to both intervals:
I₁ ∩ I₂ = (-2, 2] ∩ [1, 5)
To find the intersection, we consider the overlapping range between the two intervals:
I₁ ∩ I₂ = [1, 2]
Therefore, the intersection of the intervals I₁ and I₂ is [1, 2].
Learn more about intersections here : brainly.com/question/12089275
#SPJ11
14 . The cost of a mobile phone is pounds
The cost of a television is y pounds
When both prices are increased by £40, the ratio for the cost of the mobile phone to the cost of the television is 15:22
When both prices are decreased by £100, the ratio for the cost of the mobile phone to the cost of the television is 8:15
Find the values of x and y
Answers
Answer:
x= 260, y= 400
Step-by-step explanation:
Cost of mobile phone= x pounds
Cost of television= y pounds
When both prices are increased by £40,
cost of mobile phone= £(x +40)
cost of television= £(y +40)
\( \frac{x + 40}{y + 40} = \frac{15}{22} \)
Cross multiply:
15(y +40)= 22(x +40)
Expand:
15y +600= 22x +880
-600 on both sides:
15y= 22x +280 -----(1)
When both prices decreased by £100,
cost of mobile phone= £(x -100)
cost of television= £(y -100)
\( \frac{x - 100}{y - 100} = \frac{8}{15} \)
Cross multiply:
15(x -100)= 8(y -100)
15x -1500= 8y -800 (expand)
15x= 8y -800 +1500 (+1500 on both sides)
15x= 8y +700 (simplify)
\(x = \frac{8}{15} y + \frac{140}{3} \) -----(2)
Subst. (2) into (1):
\(15y = 22( \frac{8}{15} y + \frac{140}{3} ) + 280\)
Expand:
\(15y = \frac{176}{15} y + \frac{3080}{3} + 280 \\ 15y - \frac{176}{15} y = \frac{3080}{3} + 280 \\ \frac{49}{15} y = \frac{3920}{3} \\ y = \frac{3920}{3} \div \frac{49}{15} \\ y = 400\)
Subst. y=400 into (2):
\( x= \frac{8}{15} (400) + \frac{140}{3} \\ x = \frac{640}{3} + \frac{140}{3} \\ x = \frac{780}{3} \\ x = 260\)
where do the graphs of the linear equations 10x 12y = 14 and 5x 6y = 7 intersect?
Answers
The graphs of the linear equations 10x - 12y = 14 and 5x - 6y = 7 intersect along the entire line represented by the equations.
To find the point of intersection between the graphs of the linear equations 10x - 12y = 14 and 5x - 6y = 7, we can solve the system of equations simultaneously.
First, let's solve the second equation for x:
5x - 6y = 7
5x = 6y + 7
x = (6y + 7) / 5
Next, substitute this expression for x into the first equation:
10x - 12y = 14
10((6y + 7) / 5) - 12y = 14
12y + 14 - 12y = 14
14 = 14
The equation 14 = 14 is always true. This indicates that the two equations represent the same line and are coincident. Therefore, the graphs of the two equations overlap and intersect at all points along the line defined by the equations.
In summary, the graphs of the linear equations 10x - 12y = 14 and 5x - 6y = 7 intersect along the entire line represented by the equations.
learn more about "intersect ":- https://brainly.com/question/11006922
#SPJ11
A parabola can be drawn given a focus of (4, -3) and a directrix of y=5 Write the equation of the parabola in any form.
Answers
Answer:
The equation of the parabola is (x - 4)² = -16(y - 1)
Step-by-step explanation:
The standard form of the equation of the parabola is (x - h)² = 4p(y - k), where
The vertex of the parabola is (h, k)The focus is (h, k + p)The directrix is at y = k - p∵ The focus of the parabola is (4, -3)
∵ The focus is (h, k + p)
∴ h = 4
∴ k + p = -3 ⇒ (1)
∵ It has a directrix of y = 5
∵ The directrix of the parabola is y = k - p
∴ k - p = 5 ⇒ (2)
→ Add equations (1) and (2) to find k and p
∵ (k + k) + (p - p) = (-3 + 5)
∴ 2k + 0 = 2
∴ 2k = 2
→ Divide both sides by 2
∴ k = 1
→ Substitute the value of k in equation (1)
∵ 1 + p = -3
→ Subtract 1 from both sides
∴ 1 - 1 + p = -3 - 1
∴ p = -4
∵ The form of the equation of the parabola is (x - h)² = 4p(y - k)
→ Substitute the values of h, k, p in it
∴ (x - 4)² = 4(-4)(y - 1)
∴ (x - 4)² = -16(y - 1)
∴ The equation of the parabola is (x - 4)² = -16(y - 1)
Francine had six times the money Tommy had, but after Francine gave Tommy $33 to help him purchase a baseball cap, Tommy had twice as much as Francine. How much did they each start with?
Answers
For the relation of times of money , Francine and Tommy start with the amount of money equals to $18 and $3 respectively.
Let 'x' represents the amount of money with Francine .
And 'y' represents the amount of money with Tommy.
In the first condition:
x = 6y __(1)
To purchase baseball cap Francine gave $33 then the given relation is :
y - 33 = 2( x - 33 )
⇒ y - 33 = 2x - 66
⇒y = 2x -66 + 33
⇒ y = 2x -33 __(2)
Substitute the value of 'x' from (1) in (2) we get,
y = 2(6y) - 33
⇒y = 12y - 33
⇒ 12y - y = 33
⇒ 11y = 33
⇒ y = $3
⇒ x = 6(3)
⇒ x = $18
Therefore, the amount of money Francine and Tommy start with is equal to $18 and $3 respectively.
Learn more about money here
brainly.com/question/29452742
#SPJ4
PLS HELP ME ASAP I DONT HAVE TIME IT ALSO DETECTS IF ITS RIGHT OR WRONG

Answers
Answer:
5 hours
Step-by-step explanation:
Let x represent the amount of hours that ralph can do.
Let y represent the money he earned.
Let m represent how much he earns per hour.
Let b represent the initial fee
y=mx+b
y=33x + 24
189=33x+24
Solve for x:
189=33x+24
165 = 33x
x=5
Please help me please
Yesterday, two friends went into a bank to open savings accounts. Ted started by putting $300 in his account, and he will deposit an additional $4 each week. Carly made no initial deposit, but she will add $16 more each week. In a few weeks, the friends will have the same account balance. How many weeks will that take?
Answers
To solve this problem, we can use algebraic equations. Let's say that the number of weeks it takes for Ted and Carly to have the same account balance is "w".
Ted's account balance after "w" weeks can be represented by:
300 + 4w
Carly's account balance after "w" weeks can be represented by:
16w
We want to find out when their account balances will be equal, so we can set these two equations equal to each other:
300 + 4w = 16w
Simplifying this equation, we get:
300 = 12w
Dividing both sides by 12, we get:
25 = w
Therefore, it will take 25 weeks for Ted and Carly to have the same account balance.
Let R be the region bounded by the following curves. Use the shell method to find the volume of the solid generated when R is revolved about the y-axis. y=18x,y=18, and x=0 (Type exact answers.) A. ∫ dy B. ∫1dx
Answers
Given curves are y=18x, y=18, and x=0. We have to find the volume of the solid generated when R is revolved about the y-axis using the shell method.Let's sketch the curves first:We can see that R is the region bounded by the curves y=18x, y=18 and x=0.
We need to rotate this region around the y-axis using the shell method to find the volume of the solid generated.Let's use the shell method here:Shell method:$$\large V=2\pi \int_{a}^{b}x[f(x)-g(x)]dx$$
Here, we need to rotate R around the y-axis, therefore, a = 0 and b = 18.
From the graph, we can see that the functions $f(x)$ and $g(x)$ are as follows:$$f(x) = 18 \\ g(x) = 18x$$
Using the shell method, the volume of the solid generated is:$$\begin{aligned}V &= 2\pi \int_{0}^{18}x[18-18x]dx \\&= Therefore, the volume of the solid generated when R is revolved about the y-axis is 17496π.
Which of the following expressions is equivalent to -10? Which of the following expressions is equivalent to -10?
-7 + 3
-3 - 7
3 - 7
7 - 3
Answers
Answer:
-3-7
Step-by-step explanation:
-3-7=10
Answer:
-3 - 7.
Step-by-step explanation:
-3 - 7 = -10.
What is the domain of the relation below? A. {-1,0, 1, 3} B. {-2,0, 1, 3) C. -2,-1,0, 1, 2, 3} D. {0, 1, 2, 3)
Answers
Answer:
C
Step-by-step explanation:
Which statement correctly compares the spreads of the distributions?
A. The range of penguin heights is greater at Countyside Zoo than at
Park Zoo
B. The range of penguin heights is greater at Park Zoo than at
Countyside Zoo.
C. The mode of penguin heights at Countyside Zoo is greater than the mode at Park Zoo
D. The ranges of penguin heights are the same.

Answers
Answer:
A
Step-by-step explanation:
Range = Highest value - Lowest value
At Park Zoo:
R = 44 - 38
= 6
At Countryside Zoo;
R = 45 - 38
= 7
So, it cannot be D, because the ranges are not the same and it cannot be B because the range is greater at countryside zoo
The mode is the value that appears the moat frequently.
At Park zoo, the mode is 41 since it has the most dots.
At Countryside zoo, the mode is 40, since it has the most dots
So, it cannot be C because Park zoo has a greater Mode.
so, the only answer is A
1. Find the mean, median, and mode of each set of numbers.
a) 13 kg, 71 kg, 95 kg, 62 kg, 29 kg, 25 kg, 31 kg, 40 kg
Answers
add them up and divide by the number of numbers there are
There is no mode
that means most occurring
Median is 35.5
add them up Least to greatest the one or two in the middle take the two add them and divide by 2
example 2 major premise: no dogmatists are scholars who encourage free thinking. minor premise: some theologians are scholars who encourage free thinking. conclusion: some theologians are not dogmatists. the major premise in example 2 is an proposition. the minor premise in example 2 is an proposition. the conclusion in example 2 is an proposition. therefore, the mood of the categorical syllogism in example 2 is .
Answers
The mood of the categorical syllogism in example 2 is AIO.
In your example, we have the following premises and conclusion:
1. Major Premise: No dogmatists are scholars who encourage free thinking.
2. Minor Premise: Some theologians are scholars who encourage free thinking.
3. Conclusion: Some theologians are not dogmatists.
The major premise in example 2 is an A proposition (All S are not P). The minor premise in example 2 is an I proposition (Some S are P). The conclusion in example 2 is an O proposition (Some S are not P).
To learn more about premises, refer here:
https://brainly.com/question/29699382#
#SPJ11
The width of a rectangle measures (3s+t) centimeters,and it’s length measures (3s-9t) centimeters. Which expression represents the perimeter,in centimeters of the rectangle ?
Answers
Answer:
12s - 16t
Step-by-step explanation:
2(3s + t) + 2(3s - 9t)
6s + 2t + 6s - 18t
12s + 2t - 18t
12s - 16t
Answer:Perimeter of the rectangle =(12s -16t)centimeters.
Step-by-step explanation:
The perimeter of a rectangle is given as 2(l+w)
Given that width of the rectangle=(3s+t)centimeters. and
Length of the rectangle=(3s-9t)centimeters.
Solving we have
Perimeter= 2(l+w)
Perimeter=2(3s+t +3s-9t)
Perimeter=2(3s+3s -9t+t)
Perimeter=2(6s-8t)
Perimeter=(12s -16t)centimeters.
See related queston here : https://brainly.com/question/17288503