BRAINLIEST!!
10 POINTS!! PLZ HELP !!!!
PLEASE ANSWER STEP BY STEP
WILL MARK AS THE BRAINLIEST IF ITS THE CORRECT ANSWER
58.
Find the median of following data :
973, 927, 946, 975, 923, 912,909, 899, 998, 856, 894, 943, 916, 958
Answers
Answer:
910.5
Step-by-step explanation:
Since median is the middle number and there are two of them remaining. You take those two remaining numbers add them then you divide by two.
912+909=1821
=1821÷2
=910.5
Answer:
925
Step-by-step explanation:
You arrange the numbers from the smallest to the largest.
856,894,899,909,912,916,923,927,943,946,958,973,975,998.
Eliminate a number from the starting point and consecutively eliminate from the last point. Do this continuously.
You will be left with 923 and 927.
Add the two numbers then divide by 2.
Related Questions
I will give brainlist! :))
Answers
Answer:
THANKS!
Step-by-step explanation:
YOU HAVE AN AWESOME DAY!!
Suppose that \( \sin \theta=\frac{14}{28} \) What is the value of \( \theta \) ? Give your answer in radians and degrees. Assume that \( \theta \) is an acute angle.
Answers
The reference angle that has a sin value of 1/2 is π/6 radians or 30 degrees. Therefore, the value of θ is π/6 radians or 30 degrees.
Given that sin θ = 14/28, we can simplify this fraction by dividing both the numerator and denominator by their greatest common divisor, which is 14. This yields sin θ = 1/2.
The value of sin θ equal to 1/2 corresponds to the angle θ being π/6 radians or 30 degrees in the first quadrant.
In general, the trigonometric function sin θ represents the ratio of the length of the side opposite the angle θ to the length of the hypotenuse in a right triangle. For sin θ to be positive, the angle θ must lie in the first or second quadrant. Since we are assuming θ to be an acute angle, it falls within the first quadrant.
In the first quadrant, the reference angle that has a sin value of 1/2 is π/6 radians or 30 degrees. Therefore, the value of θ is π/6 radians or 30 degrees.
Learn more about reference angle here
https://brainly.com/question/16884420
#SPJ11
similar to 4.1.23 in rogawski/adams. use the linear approximation to estimate δf=e−0.3−1. what is f(x)? f(x)=
Answers
To estimate δf = \(e^(-0.3)\) - 1 using linear approximation, we can start by finding the tangent line to the curve of the function f(x) at the given point x = -0.3. This can be done by calculating the derivative of f(x) and evaluating it at x = -0.3.
Let's assume the function f(x) is given by f(x) = \(e^x\). Taking the derivative of f(x) with respect to x, we have f'(x) = \(e^x.\)
Now, we can evaluate the derivative at x = -0.3:
f'(-0.3) = e^(-0.3).
This gives us the slope of the tangent line at x = -0.3. Next, we use the point-slope form of a line to find the equation of the tangent line:
y - f(-0.3) = f'(-0.3) * (x - (-0.3)).
Since f(-0.3) = \(e^(-0.3)\), we have:
y - e^(-0.3) = e^(-0.3) * (x + 0.3).
This equation represents the linear approximation of f(x) near x = -0.3. To estimate δf = e^(-0.3) - 1, we can evaluate the above equation at x = -0.3:
\(f(x) = e^(-0.3) * (x + 0.3) + e^(-0.3).\)
Hence, \(f(x) = e^(-0.3) * x + e^(-0.3) * 0.3 + e^(-0.3).\)
\(f(x) = e^(-0.3) * x + 2 * e^(-0.3).\)
Learn more about linear approximation here:
https://brainly.com/question/30403460
#SPJ11
g the sequence is decreasing and bounded below by 0. explain in clear english (briefly) why this means it must have a limit.
Answers
Since the sequence is always decreasing and cannot go below the lower bound, it becomes increasingly closer to the lower bound, and thus converges to a limit.
A sequence is said to be decreasing if each term is smaller than the previous one, and bounded below if there exists a lower bound such that no term in the sequence is smaller than this bound. In this case, the sequence is decreasing and bounded below by 0.
When a sequence is both decreasing and bounded below, it must have a limit because the terms cannot continue to decrease indefinitely, as they cannot go below the lower bound (in this case, 0). This means that as we progress through the terms of the sequence, the difference between consecutive terms will decrease and eventually approach a constant value.
The limit of a sequence is a value that the terms of the sequence approach as they get closer and closer to the end. In this situation, the limit is the smallest possible value that the sequence can approach, without going below the lower bound.
for such more questions on sequence
https://brainly.com/question/7882626
#SPJ11
the frequency distribution below summarizes employee years of service for alpha corporation. find the class midpoint for class .
Answers
The class midpoint for each class interval in the frequency distribution has been calculated.
A frequency distribution is a method of organizing data, especially raw data, in a statistical or graphical representation so that the occurrence of each variable is apparent.
In statistics, the frequency distribution is used to understand how many times each value appears in a set of data, which is essential to making decisions in a range of businesses and industries.
Alpha Corporation's employee years of service were used to create a frequency distribution that looks like this:
Years Of Service Number of Employees0-4 56-9 1010-14 1015-19 820-24 3
The class midpoint is halfway between the upper and lower boundaries of a class interval, represented by an "X" or a dot. The frequency distribution's class interval is represented by (0-4), (5-9), (10-14), (15-19), and (20-24).To compute the class midpoint, use the formula:
X = (Lower Bound + Upper Bound) / 2For class (0-4), the lower and upper bounds are 0 and 4, respectively.
Therefore, the class midpoint would be calculated as follows:
X = (0 + 4) / 2 = 2For class (5-9), the lower and upper bounds are 5 and 9, respectively.
Therefore, the class midpoint would be calculated as follows:
X = (5 + 9) / 2 = 7For class (10-14), the lower and upper bounds are 10 and 14, respectively.
Therefore, the class midpoint would be calculated as follows:
X = (10 + 14) / 2 = 12
For class (15-19), the lower and upper bounds are 15 and 19, respectively.
Therefore, the class midpoint would be calculated as follows:
X = (15 + 19) / 2 = 17
For class (20-24), the lower and upper bounds are 20 and 24, respectively.
Therefore, the class midpoint would be calculated as follows:
X = (20 + 24) / 2 = 22
Thus, the class midpoint for each class interval in the frequency distribution has been calculated.
Learn more about frequency distribution from the given link!
https://brainly.com/question/30955749
#SPJ11
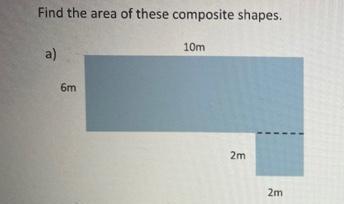
Name: Lattelibas Bovan
Area
Find the area of the composite shapes.
5m
5m
Stambe
Resources
1.
10m
5m
5m
3m
5m
13m
Area
Answers
The area of the composite shape is 64 square meters
How to determine the area of the composite shape?The shape that completes the question is added as an attachment
From the attached figure, we have the following shapes:
The area of the square is
Area = Length^2
The area of the rectangle is
Area = Length * Width
So, the area of the composite shape is
Area = 2 * 2 + 10 * 6
Evaluate
Area = 64
Hence, the area of the composite shape is 64 square meters
Read more about areas at:
https://brainly.com/question/24487155
#SPJ1
Find the area of the circle. Round your answer to the nearest hundredth. It is a whole circle with a diameter of twelve, use the formula a=pi r ^2. I'll give 45 points and brainliest quick pls I have 15 minutes
Answers
Answer: 113
Step by Step explanation:
12/2=6
inches.π⋅6^2≈113
The area of the circle with diameter 12 units is 113.04 square units.
What is Circle?A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre.
The given circle has a diameter of 12.
We have to find the area of the circle.
The formula for Area of circle=πr²
Radius of circle = Diameter/2
=12/2
Radius=6
Now let us put r value in Area of circle formula
A=3.14×6²
=3.14×36
=113.04 square units.
Hence, the area of the circle with diameter 12 units is 113.04 square units.
To learn more on Circles click:
https://brainly.com/question/11833983
#SPJ5
Imran Farhat and Abdul Razzaq enhanced 69 runs in
the score of pakistan, if the score of Abdul
Razzaq is double than the score of Imran Farhat.
How many runs Abdul Razzaq requires to complete
his half century.
Answers
Answer:
4 runs
Step-by-step explanation:
x = Farhat's run
x+2x=69
3x=69
x=69/3
x=23
Therefore, Abdul Razzaq has hit 2x runs = 2x23 = 46 runs.
He needs 4 more runs for a half century.
A certain surgery has a 70hance of success. the surgery is performed on three patients. find the probability of the surgery being successful on exactly two patients.
Answers
According to the given statement the probability of the surgery being successful on exactly two patients is 0.441 & 44.1%.
To find the probability of the surgery being successful on exactly two patients, we can use the binomial probability formula.
The formula for the probability of exactly k successes in n trials, when the probability of success in a single trial is p, is given by:
P(X = k) = nCk × \(p^{k}\) × \((1-p)^{n-k}\)
In this case,
n (number of trials) is 3 (since the surgery is performed on three patients),
p (probability of success) is 0.7 (given that the surgery has a 70% chance of success),
and
k (number of successes) is 2 (since we want exactly two successful surgeries).
Plugging the values into the formula, we have:
P(X = 2) = 3C2 × 0.7² × (1-0.7)³⁻²
Simplifying the calculation:
P(X = 2) = 3 × 0.7² × 0.3¹
Calculating the result:
P(X = 2) = 0.441
Therefore, the probability of the surgery being successful on exactly two patients is 0.441, or 44.1%.
To know more about probability visit :
https://brainly.com/question/31828911
#SPJ11
The probability of the surgery being successful on exactly two out of three patients is 0.441 or 44.1%.
The probability of the surgery being successful on exactly two patients can be found using the binomial probability formula.
The formula for the probability of exactly x successes in n trials, when the probability of success in each trial is p, is given by:
\(P(x) = (n_C_x) * p^x * (1-p)^{n-x}\)
In this case, the probability of success (the surgery being successful) is 0.7, as stated in the question.
Since the surgery is performed on three patients (n = 3), we want to find the probability of exactly two successful surgeries (x = 2).
Plugging these values into the formula, we get:
\(P(2) = (3_C_2) * 0.7^2 * (1-0.7)^{(3-2)}\)
Calculating the values, we find:
\(P(2) = 3 * 0.7^2 * 0.3^1\)
\(P(2) = 3 * 0.49 * 0.3\)
\(P(2) = 0.441\)
Therefore, the probability of the surgery being successful on exactly two patients is 0.441 or 44.1%.
In conclusion, the probability of the surgery being successful on exactly two out of three patients is 0.441 or 44.1%.
Learn more about probability from the given link:
https://brainly.com/question/32117953
#SPJ11
Members at a popular fitness club currently pay a $40 per month membership fee. The owner of the club wants to raise the fee to $50 but is concerned that some members will leave the gym if the fee increases. To investigate, the owner plans to survey a random sample of the club members and construct a 95% confidence interval for the proportion of all members who would quit if the fee was raised to $50.
(a) Explain the meaning of "95% confidence" in the context of the study.
(b) After the owner conducted the survey, he calculated the confidence interval to be 0.18 0.075 Interpret this interval in the context of the study.
(c) According to the club's accountant, the fee increase will be worthwhile if fewer than 20% of the members quit. According to the interval from part (b), can the owner be confident that the fee increase will be worthwhile? Explain.
(d) One of the conditions for calculating the confidence interval in part (b) is that and. Explain why it is necessary to check this condition.
Answers
Answer:(a) "95% confidence" means that if we were to repeat this study many times, we would expect the true proportion of members who would quit to be within the calculated interval for 95% of those studies. In other words, we can be 95% confident that the true proportion of members who would quit falls within the interval.
(b) The interval is [0.18, 0.075]. This means that we are 95% confident that the true proportion of members who would quit if the fee was raised to $50 falls between 0.18 and 0.075.
(c) No, the owner cannot be confident that the fee increase will be worthwhile because the interval from part (b) includes 20%. If the true proportion of members who would quit is 20%, then the fee increase would not be worthwhile. Since the interval includes 20%, we cannot be confident that the true proportion is less than 20%.
(d) One of the conditions for calculating the confidence interval is that the sample size is large enough and that the number of successes and failures in the sample are both at least 10. This is necessary because the interval calculation relies on the normal distribution, which is only valid when the sample size is large enough and the number of successes and failures are both at least 10. If this condition is not met, then the interval calculation may not be accurate or valid.
Step-by-step explanation:
What is the answer to the question?
Help help help help me
This is very important (◕દ◕)

Answers
9514 1404 393
Answer:
C) √3
Step-by-step explanation:
The repeating decimals are both single digits, beginning at the decimal point. So, their equivalent is that digit divided by 9:
\(0.\overline{4}=\dfrac{4}{9}\\\\0.\overline{9}=\dfrac{9}{9}=1\)
This means the given expression can be simplified to ...
\(\dfrac{3\sqrt{0.\overline{4}}+\sqrt{0.\overline{9}}}{\sqrt{3}}=\dfrac{3\sqrt{\dfrac{4}{9}}+\sqrt{\dfrac{9}{9}}}{\sqrt{3}}=\dfrac{3\cdot\dfrac{2}{3}+1}{\sqrt{3}}=\dfrac{3}{\sqrt{3}}=\boxed{\sqrt{3}}\)
in a field hockey championship, 120 matches were played. every pair of team played one match with each other. the number of teams in the tournament is therefore:
Answers
The number of teams in the field hockey championship tournament is 16.
The total number of matches played in the field hockey championship are 120 matches.
Each pair of team played one match with each other.
So, let us say that there are N teams in the tournament.
So, we can chose any two teams for a match,
So, applying the permutation formula,
ⁿC₂ = 120
Solving further,
N!/2!(N-2)! = 120
N(N-1)/2 = 120
N(N-1) = 240
On observing closely and applying hit and trial method,
16(15) = 240
So, the values of N is 16.
Hence, 16 teams participated in the tournament.
To know more about permutations, visit,
https://brainly.com/question/1216161
#SPJ4
Question 3 Find whether the vectorrs are parallel. (-2,1,-1) and (0,3,1)
a. Parallel
b. Collinearly parallel
c. Not parallel
d. Data insufficient
Answers
To determine whether the vectors (-2,1,-1) and (0,3,1) are parallel, we need to compare their direction. If they have different directions, they are not parallel. the correct answer is option c) Not parallel.
To check if two vectors are parallel, we can compare their direction vectors. The direction vector of a vector can be obtained by dividing each component of the vector by its magnitude. In this case, let's calculate the direction vectors of the given vectors.
The direction vector of (-2,1,-1) is obtained by dividing each component by the magnitude:
Direction vector of (-2,1,-1) = (-2/√6, 1/√6, -1/√6)
The direction vector of (0,3,1) is obtained by dividing each component by the magnitude:
Direction vector of (0,3,1) = (0, 3/√10, 1/√10)
Comparing the direction vectors, we can see that they are not equal. Therefore, the vectors (-2,1,-1) and (0,3,1) are not parallel. Hence, the correct answer is option c) Not parallel.
Learn more about vectors here:
https://brainly.com/question/24256726
#SPJ11
45. a survey conducted by the american automobile association showed that a family of four spends an average of $215.60 per day while on vacation. suppose a sample of 64 families of four vacationing at niagara falls resulted in a sample mean of $252.45 per day and a sample standard deviation of $74.50. develop a 95% confidence interval estimate
Answers
The required 95% confidence interval representing the true population mean falls within the given interval, based on the given sample mean is equals to (233.00, 271.90).
Use the t-distribution,
To construct a confidence interval for the population mean,
The sample size is relatively small (n = 64)
And the population standard deviation is unknown.
The formula for the confidence interval is,
\(\bar{x}\) ± tα/2 × (s/√n)
where \(\bar{x}\) is the sample mean,
s is the sample standard deviation,
n is the sample size,
And tα/2 is the critical value of the t-distribution with (n-1) degrees of freedom, corresponding to the desired confidence level.
For a 95% confidence interval, the critical value of the t-distribution with 63 degrees of freedom is approximately 1.998.
Plugging in the given values, we get,
252.45 ± 1.998 × 74.50/√64)
Simplifying we get,
252.45 ± 19.45
This implies,
The 95% confidence interval for the mean amount spent per day by a family of four visiting Niagara Falls is (233.00, 271.90)
Therefore, 95% confidence interval that the true population mean falls within this interval, based on the given sample is (233.00, 271.90).
learn more about confidence interval here
brainly.com/question/29770601
#SPJ4
The above question is incomplete , the complete question is:
A survey conducted by the American automobile association showed that a family of four spends an average of $215.60 per day while on vacation. suppose a sample of 64 families of four vacationing at Niagara falls resulted in a sample mean of $252.45 per day and a sample standard deviation of $74.50.
a. Develop a 95% confidence interval estimate of the mean amount spent per day by a family of four visiting Niagara Falls (to 2 decimals).
Find the common difference of the arithmetic sequence -11,-17,-23....
Answers
Answer:
d = - 6
Step-by-step explanation:
the common difference d is the difference between consecutive terms in the sequence.
- 17 - (- 11) = - 17 + 11 = - 6
- 23 - (- 17) = - 23 + 17 =- 6
the common difference d = - 6
The perimeter of a rectangle is 44 inches, and its area is 112 square inches. Find the length and the width of the rectangle. 2. Find two consecutive odd integers with sum of squares equal to 74. 3. Find two real numbers with a sum of 10, and a product of 22. 4. Solve -x² + 6x + 7 ≥ 0. 1. f(x)=x²-8x + 12 2. f(x)=x²-9 3. f(x)= x² + 14x + 45 4. f(x)= 3(x-1)² - 2 5. f(x) = (x - 5)² - 4 6. f(x) = (x + 2)² - 1
Answers
1. The length is 14 inches and the width is 8 inches. 2. The two consecutive odd integers with a sum of squares equal to 74 are 5 and 7. 3. The two real numbers with a sum of 10 and a product of 22 are 2 and 8. 4. The solution to the inequality -x² + 6x + 7 ≥ 0 is x ≤ -1 or x ≥ 7.
1. To find the length and width of the rectangle, we can set up two equations. Let L be the length and W be the width. We know that 2L + 2W = 44 (perimeter) and L * W = 112 (area). Solving these equations simultaneously, we find L = 14 inches and W = 8 inches.
2. Let the two consecutive odd integers be x and x + 2. The sum of their squares is x² + (x + 2)². Setting this equal to 74, we get x² + (x + 2)² = 74. Expanding and simplifying the equation gives x² + x² + 4x + 4 = 74. Combining like terms, we have 2x² + 4x - 70 = 0. Factoring this quadratic equation, we get (x - 5)(x + 7) = 0. Therefore, the possible values for x are -7 and 5, but since we need consecutive odd integers, the solution is x = 5. So the two consecutive odd integers are 5 and 7.
3. Let the two real numbers be x and y. We know that x + y = 10 (sum) and xy = 22 (product). From the first equation, we can express y as y = 10 - x. Substituting this into the second equation, we get x(10 - x) = 22. Expanding and rearranging terms, we have -x² + 10x - 22 = 0. Solving this quadratic equation, we find x ≈ 2.28 and x ≈ 7.72. Therefore, the two real numbers are approximately 2.28 and 7.72.
4. To solve the inequality -x² + 6x + 7 ≥ 0, we can first find the roots of the corresponding quadratic equation -x² + 6x + 7 = 0. Using factoring or the quadratic formula, we find the roots to be x = -1 and x = 7. These roots divide the number line into three intervals: (-∞, -1), (-1, 7), and (7, ∞). We can then test a point from each interval to determine if it satisfies the inequality. For example, plugging in x = -2 gives us -(-2)² + 6(-2) + 7 = 3, which is greater than or equal to 0. Therefore, the solution to the inequality is x ≤ -1 or x ≥ 7.
Learn more about rectangle here: https://brainly.com/question/15019502
#SPJ11
HELPPPPPPPPPPPPPPPPPPPPPPPPP

Answers
Answer:
SAS
Step-by-step explanation:
When f = 2 and g = 8, n = 4. If n varies jointly with f and g, what is the constant of variation?
Answers
Answer:
The constant of variation is ¹/₄.
Step-by-step explanation:
When n varies jointly with f and g, we can write the following equation:
\(\boxed{n \propto fg \implies n = kfg}\)
where k is the constant of variation.
We are given that f = 2, g = 8, and n = 4.
Substitute these values into the equation:
\(\implies 4 = k \cdot 2 \cdot 8\)
Solve for k:
\(\implies 4 = 16k\)
\(\implies \dfrac{4}{16} = \dfrac{16k}{16}\)
\(\implies \dfrac{1}{4}=k\)
Therefore, the constant of variation is ¹/₄.
\(\blue{\huge {\mathrm{CONSTANT \; VARIATION}}}\)
\(\\\)
\({===========================================}\)
\({\underline{\huge \mathbb{Q} {\large \mathrm {UESTION : }}}}\)
When f = 2 and g = 8, n = 4. If n varies jointly with f and g, what is the constant of variation?\({===========================================}\)
\( {\underline{\huge \mathbb{A} {\large \mathrm {NSWER : }}}} \)
The constant of variation is 1/4.\({===========================================}\)
\({\underline{\huge \mathbb{S} {\large \mathrm {OLUTION : }}}}\)
If n varies jointly with f and g, the relationship between them can be written as:
\(\sf n = k \times f \times g\)where:
k is the constant of variation.Using the given information, we can solve for k as follows:
\(\begin{aligned}\sf n&=\sf k\times f\times g \\\sf 4& =\sf k\times 2\times 8 \\\sf 4& =\sf 16k \\\sf k& =\sf \dfrac{4}{16} \\\sf k& =\sf \dfrac{1}{4}\end{aligned}\)Therefore, the constant of variation is 1/4.
\({===========================================}\)
359 divided by 19 can you tell me please
Answers
Answer:
18.8947368
Step-by-step explanation:
Answer: 18.8947368421
Step-by-step explanation:
6 : 4 is equivalent to
Answers
Answer:
12 : 8, 18 : 12, 24 : 16, 30 : 20
Step-by-step explanation:
These are the four after 6:4. I didn't know which you needed.
Answer:
3:2
Step-by-step explanation:
If you want to simplify 6:4, it also makes an equivalent equation. To simplify this, we divide by the greatest number that both numbers can be evenly divided by. 6 and 4 can both be divided by 2, which is the biggest number we can divide both numbers by.
6/2=3
4/2=2
The ratio is now simplified/equivalent to 3:2.
I hope this helps...have an amazing day c:
The davidson family wants to expand its rectangular patio, which currently measures 15 ft by 12 ft. they want to extend the length and width the same amount to increase the total area of the patio by 160 ft2. which quadratic equation best models the situation? a = lw (15)(12) (x)(x) = (15)(12) 160 (15x)(12x) = (15)(12) 160 2(15 x) 2(12 x) = (15)(12) 160 (15 x)(12 x) = (15)(12) 160
Answers
Answer:
160
Step-Step Explaining:
So I Know This ⏩ ⏩
y ticket. each ticket has a probability of 0.3 of winning a prize. after seven days, what is the probability that jorge has won at least one prize? round your answer to four decimal places.
Answers
Jorge has a ticket has a probability of 0.3 of winning a prize. after seven days, probability that jorge has won at least one prize is 0.9176
Let the probability of Jorge winning be 0.3 so ,
Probability of not winning be (1-0.3)⁷
(0.7)⁷
= 0.0823
Therefore, Jorge not winning is 0.0823.
If he wins at least one prize is,
1 - P(win nothing)
1 - 0.0823
= 0.9176
Therefore, the probability that the Jorge wins at least one prize is 0.9176.
Probability refers to potential. A random event's occurrence is the subject of this area of mathematics. The range of the value is 0 to 1. Mathematics has included probability to forecast the likelihood of certain events. The degree to which something is likely to happen is basically what probability means.
Learn more about Probability:
https://brainly.com/question/29643139
#SPJ4
which of the following is the midpoint riemann sum approximation of ∫64x3 1−−−−−√ⅆx using 4 subintervals of equal width?
Answers
The midpoint Riemann sum approximation of ∫64x3 1−−−−−√ⅆx using 4 subintervals of equal width is 9980
The midpoint Riemann sum approximation of ∫64x3 1−−−−−√ⅆx using 4 subintervals of equal width is calculated by summing the area of each subinterval under the midpoint of the interval.
The formula for the midpoint Riemann sum is given by:
Sum = (width of interval) * (height of midpoint)
For this problem, since the width of each interval is 16/4 = 4, the midpoint Riemann sum is calculated by:
Sum = 4 * (1 + (16/4)^3 + (32/4)^3 + (48/4)^3)
Substituting the values for each midpoint, we get the following equation:
Sum = 4 * (1 + 4^3 + 8^3 + 12^3)
This simplifies to:
Sum = 4 * (1 + 64 + 512 + 1728)
Therefore, the midpoint Riemann sum approximation of ∫64x3 1−−−−−√ⅆx using 4 subintervals of equal width is:
Sum = 4 * (2495)
Sum = 9980
Learn more about Riemann sum here:
https://brainly.com/question/30241844
#SPJ4
2
1.
Find the perimeter
the
triangle
60°
90°
Find
area
length of
45
Right Triangles, Ares, Sectors
O
8
30 T/b
5
of sector AOB and
are AB
of
ов
bel
ans
a
N
fr
e

Answers
a. The perimeter of the triangle is 12+4√3
b. The area of the sector AOB and length of arc AB are 29.4 and 11.8 respectively
What is length of arc?Arc length is defined as the distance along the part of the circumference of any circle or any curve (arc).
The perimeter of a shape is the addition of all the sides of a shape.
A sector is the space bounded by an arc and the radii of a circle.
a. The other two sides of the triangle is calculated as,
sin 30 = x/ 8
1/2 = x/8
x = 4
cos 30 = y/8
√3/2 = y/8
8√3 = 2y
y = 4√3
The perimeter of the triangle = 4+4√3+ 8
= 12+4√3 unit
b. The area of sector = (tetha)/360 × πr²
= 135/360 × 3.14× 5²
= 10597.5/360
= 29.4 unit²
The length of the arc = (tetha)/360 × 2πr
= 135/360 × 2 × 3.14 × 5
= 4239/360
= 11.8units
learn more about length of an arc from
https://brainly.com/question/2005046
#SPJ1
My entire life I have noted the sun rises every morning and sets every evening. I am concluding that the sun will rise tomorrow morning and set tomorrow evening. Make an argument as to why this can be inductive or deductive reasoning and include details that indicate your knowledge of the topic.
Answers
The argument that the sun will rise tomorrow morning and set tomorrow evening is based on inductive reasoning, using past observations of consistent sunrise and sunset patterns to predict future occurrences.
1. The observation: Throughout your entire life, you have consistently noticed that the sun rises every morning and sets every evening. This is an observation based on personal experience.
2. Inductive reasoning: Based on this observation, you make an inference or prediction about the future. You reason that since the sun has always risen in the morning and set in the evening in the past, it is likely to continue doing so in the future.
3. Pattern and consistency: The assumption is that natural phenomena, such as the rising and setting of the sun, follow a pattern or regularity. This assumption is based on the principle of uniformity of nature, which suggests that the future will resemble the past in terms of natural occurrences.
4. The limitations of inductive reasoning: While inductive reasoning provides a useful way to make predictions based on past observations, it is not foolproof. There is always a small possibility that something unexpected could happen, such as a rare astronomical event or an external factor that alters the pattern. However, based on the available evidence and the consistency of the observed pattern, the prediction that the sun will rise tomorrow morning and set tomorrow evening is highly probable.
In summary, the argument relies on inductive reasoning, using the past consistent observation of the sun's rising and setting to predict that it will continue to do so in the future. While this reasoning is not infallible, it is a reasonable and practical way to make predictions based on observed patterns in nature.
Learn more about inductive reasoning: https://brainly.com/question/1490615
#SPJ11
Can some one answer this?

Answers
9514 1404 393
Answer:
(c) 2
Step-by-step explanation:
A graph shows the zeros are -5, -3, 0, 2. Of these, only 2 is on your list.
2 is a zero of the expression

Select the procedure that can be used to show the converse of the
Pythagorean theorem using side lengths chosen from 2 cm, 3 cm, 4 cm, and
5 cm.
A. Knowing that 2^2 + 4^2 < 5^2, draw the 2 cm side and the 4 cm side
with a right angle between them. The 5 cm side will fit to form a right triangle.
B. Knowing that 3^2 +4^2 = 5^2, draw any two of the sides with a right angle between them. The third side will fit to form a right triangle.
C. Knowing that 3^2 +4^2 = 5^2, draw the 3 cm side and the 4 cm side with a right angle between them. The 5 cm side will fit to form a right triangle.
D. Knowing that 2^2 + 3^2 4^2, draw the 2 cm side and the 3 cm side with a right angle between them. The 4 cm side will fit to form a right triangle.
Answers
The procedure that can be used to show the converse of the Pythagorean theorem using side lengths chosen from 2 cm, 3 cm, 4 cm, and 5 cm is option C.
Knowing that 3^2 +4^2 = 5^2, draw the 3 cm side and the 4 cm side with a right angle between them. The 5 cm side will fit to form a right triangle.
The Pythagorean Theorem is a relationship that exists between the sides of a right triangle, which is a triangle with one interior angle of 90 degrees. According to the Pythagorean Theorem, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
The Converse of the Pythagorean Theorem is an inverse statement that implies that if a triangle's sides satisfy the relationship described in the Pythagorean Theorem, then the triangle is a right triangle.
To know more about Pythagorean visit:
https://brainly.com/question/28032950
#SPJ11
What is the slope of the line that contains the points (-2, 2) and (3, 4)?
A -2/5
B 2/5
C 5/2
D -5/2
Answers
Answer:
\(B) ~\dfrac 25\)
Step-by-step explanation:
\(\text{Given that,} ~ (x_1,y_1) = (-2,2)~ \text{and}~ (x_2 ,y_2) = (3,4)\\\\\text{Slope},~ m = \dfrac{y_2 - y_1}{x_2 -x_1}\\\\\\~~~~~~~~~~~~~=\dfrac{4-2}{3+2}\\\\\\~~~~~~~~~~~~~=\dfrac 25\)
Hi student, let me help you out! :)
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
We are asked to find the slope of the line that contains the points (-2, 2) and (3, 4).
\(\triangle~\fbox{\bf{KEY:}}\)
Use the slope formula, which is given below:\(\star~\mathrm{\cfrac{y2-y1}{x2-x1}}\)
Where
y2 and y1 are y-coordinates
x2 and x1 are x-coordinates
Substitute the values:
\(\star~\mathrm{\cfrac{4-2}{3-(-2)}}\)
Simplify!
\(\star~\mathrm{\cfrac{2}{5}}\)
Hope it helps you out! :D
Ask in comments if any queries arise.
#StudyWithBrainly
~Just a smiley person helping fellow students :)
Tom the painter is painting window frames on a house. He knows that the angle his ladder should make with the ground should be between 55° and 35° in order to be safe. Tom's ladder is 8m and he wishes to paint a window frame 6.3m above the ground.
Is Tom's ladder safe to use?
Answers
Answer:
Tom should use a ladder that is smaller or at the the same height of the window frame. Here it says that he is using a ladder that is taller than the window frame, and this can be very uncomfortable for the person who is using the ladder, so it would be recommendable for Tom to use a smaller ladder, probably a ladder that is only a few inches smaller or taller than the window frame. Using a ladder that is like this should be safe to use.
Step-by-step explanation:
Hope this helps =)
Nine less than 2/3 of a number is 11
Answers
Answer:
30
Step-by-step explanation:
let 'n' = a number
\(\frac{2n}{3}\) - 9 = 11
2n = 20
3
cross-multiply: 2n = 60
n = 30