Which statement BEST describes how to find the distance between -5 and 15?
A) Add -5 and 15.
B) Subtract 15 from -5
C) Subtract 5 from 15.
D) Subtract -5 from 15, then find the absolute value.
Answers
Answer:
D) Subtract -5 from 15, then find the absolute value
Step-by-step explanation:
Related Questions
The number of three-digit numbers with distinct digits that can be formed using the digits 1, 2, 3, 5, 8, and 9 is what
. The probability that both the first digit in the last digit of the three digit number are even numbers is what
Answers
The requried, probability that both the first digit in the last digit of the three-digit number is even numbers is 20%.
To count the number of three-digit numbers with distinct digits that can be formed using the digits 1, 2, 3, 5, 8, and 9, we can use the permutation formula:
P(n, r) = n! / (n-r)!
In this case, we have n = 6 (since we have 6 digits to choose from) and r = 3 (since we want to form three-digit numbers). Using the formula, we get:
P(6, 3) = 120
We can choose the first digit in two ways (2 or 8), and we can choose the last digit in three ways (2, 8, or 6). For the middle digit, we have four digits left to choose from (1, 3, 5, or 9), since we cannot repeat digits. Therefore, the number of three-digit numbers with distinct digits that have an even first and last digit is:
2 x 4 x 3 = 24
The total number of three-digit numbers with distinct digits is 120, so the probability that a randomly chosen three-digit number with distinct digits has an even first and last digit is:
24/120 = 0.2 or 20%
Learn more about probability here:
brainly.com/question/14290572
#SPJ1
slope of secant line=?
slope of secant line=?
slope of tangent line=?
y=?

Answers
Therefore, the equation of the tangent line at (5,f(5)) is y = 18x - 65.
What is slope?In mathematics, the slope of a line is a measure of its steepness or incline, usually denoted by the letter m. It describes the rate of change of a line in the vertical direction compared to the horizontal direction. The slope of a line can be positive, negative, zero, or undefined, depending on the angle it makes with the horizontal axis. The slope of a line is commonly calculated as the ratio of the change in the y-coordinates to the change in the x-coordinates between any two points on the line.
Here,
(A) The slope of the secant line joining (2,f(2)) and (7,f(7)) is given by:
slope = (f(7) - f(2)) / (7 - 2)
We can find f(7) and f(2) by substituting 7 and 2, respectively, into the function f(x):
f(7) = 7² + 8(7) = 49 + 56 = 105
f(2) = 2² + 8(2) = 4 + 16 = 20
Substituting these values into the formula for the slope of the secant line, we get:
slope = (105 - 20) / (7 - 2) = 85 / 5 = 17
Therefore, the slope of the secant line joining (2,f(2)) and (7,f(7)) is 17.
(B) The slope of the secant line joining (5,f(5)) and (5+h,f(5+h)) is given by:
slope = (f(5+h) - f(5)) / (5+h - 5) = (f(5+h) - f(5)) / h
We can find f(5) and f(5+h) by substituting 5 and 5+h, respectively, into the function f(x):
f(5) = 5² + 8(5) = 25 + 40 = 65
f(5+h) = (5+h)² + 8(5+h) = 25 + 10h + h² + 40 + 8h = h² + 18h + 65
Substituting these values into the formula for the slope of the secant line, we get:
slope = ((h² + 18h + 65) - 65) / h = h² / h + 18h / h = h + 18
Therefore, the slope of the secant line joining (5,f(5)) and (5+h,f(5+h)) is h+18.
(C) The slope of the tangent line at (5,f(5)) is equal to the derivative of the function f(x) at x=5. We can find the derivative of f(x) as follows:
f(x) = x² + 8x
f'(x) = 2x + 8
Substituting x=5, we get:
f'(5) = 2(5) + 8 = 18
Therefore, the slope of the tangent line at (5,f(5)) is 18.
(D) The equation of the tangent line at (5,f(5)) can be written in point-slope form as:
y - f(5) = m(x - 5)
where m is the slope of the tangent line, which we found to be 18. Substituting the values of m and f(5), we get:
y - 65 = 18(x - 5)
Simplifying, we get:
y = 18x - 65
To know more about slope,
https://brainly.com/question/30088055
#SPJ1
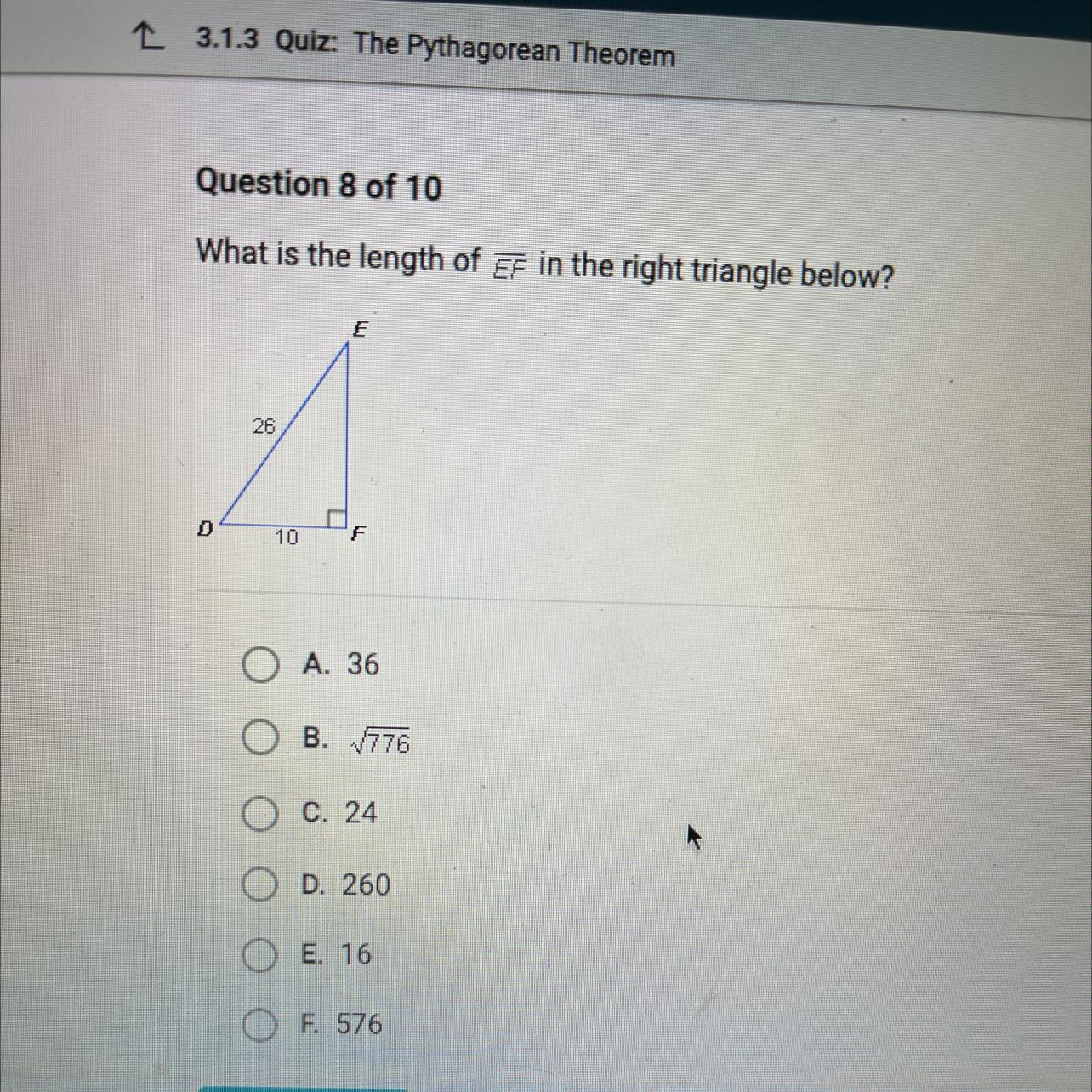
What is the length of EF in the right triangle below?
D
26
10
E
F
Answers
The measure of side length EF in the right triangle is 24.
What is the measure of side length EF?The Pythagorean theorem states that the "square on the hypotenuse of a right-angled triangle is equal in area to the sum of the squares on the other two sides.
It is expressed as;
c² = a² + b²
From the diagram:
Hypotenuse DE = c = 26
Leg DF = a = 10
Leg EF = b = ?
Plug in the values and solve for b:
c² = a² + b²
26² = 10² + b²
676 = 100 + b²
b² = 676 - 100
b² = 576
b = +√576 ( we take the positive value since we are dealing with dimensions)
b = 24
Therefore, the length EF is 24.
Option C)24 is the correct answer.
Learn more about Pythagorean theorem here: brainly.com/question/343682
#SPJ1
help!!!! please <33333


Answers
Hello!
For this you would just need to multiple straight across. Here's how you would set it up:
3/4 ·1/8
Then you would multiple 3 x 1 = 3
And 4 x 8 =32
Your answer should be 3/32, it cannot be simplified so that is the final answer :).
All boxes with a square base, an open top, and a volume of 220 ft cubed have a surface area given by S(x)equalsx squared plus StartFraction 880 Over x EndFraction , where x is the length of the sides of the base. Find the absolute minimum of the surface area function on the interval (0,infinity). What are the dimensions of the box with minimum surface area?
Answers
Answer:
Length of the sides of the base (x) = 7.606 ft
Height (h) = 3.802 ft
The minimum surface area is 173.55 ft²
Step-by-step explanation:
Surface area is given by:
\(S(x) = x^2+\frac{880}{x}\)
The value of x for which the derivate of the surface area function is zero, is the length of the sides of the base that minimizes surface area:
\(S(x) = x^2+\frac{880}{x} \\\frac{dS(x)}{dx}=0=2x-\frac{880}{x^2}\\x^3=440\\x=7.606\ ft\)
The height of the box is given by:
\(V=hx^2\\220 =h*7.606^2\\h=3.802\ ft\)
The dimensions of the box with minimum surface area are:
Length of the sides of the base (x) = 7.606 ft
Height (h) = 3.802 ft
The absolute minimum is:
\(S(x) = 7.606^2+\frac{880}{7.606}\\S_{min}=173.55\ ft^2\)
The minimum surface area is 173.55 ft²
Answer:
The absolute minimum of the surface area\(=173.55$ ft^2\)
At the minimum surface area,
Base length=7.61 feetHeight of 3.8 feet.Step-by-step explanation:
Volume of the box =220 cubic feet.
\(\text{Surface Area, } S(x)=x^2+\dfrac{880}{x}\)
To find the absolute minimum of the surface area function on the interval \((0,\infty)\), we take the derivative of S(x) and solve for its critical points.
\(S(x)=\dfrac{x^3+880}{x}\\S'(x)=\dfrac{2x^3-880}{x^2}\\$Setting the derivative equal to 0\\S'(x)=\dfrac{2x^3-880}{x^2}=0\\2x^3-880=0\\2x^3=880\\$Divide both sides by 2\\x^3=440\)
Take the cube root of both sides
\(x=\sqrt[3]{440}\\ x=7.61$ ft\)
Therefore, the absolute minimum of the surface area function on the interval \((0,\infty)\), is:
\(S(x)=\dfrac{7.61^3+880}{7.61}\\\\=173.55$ ft^2\)
Since the volume of the box =220 cubic feet
\(V=x^2h\\220=7.61^2 \times h\\h=220 \div 7.61^2\\h=3.80 ft\)
The dimensions of the box with the minimum surface area are base length of 7.61 feet and height of 3.8 feet.
Which expression is equivalent to 15 plus 3 x?
Answers
Answer:
3(5+x)
Step-by-step explanation:
Another expression that can equal 15+3x is 3(5+x)
Use Distributive Property:
3(5+x)
=15 + 3x.
I wish you the best of luck, and hopefully this is an option on your homework!
Nolan was given a box of assorted chocolates for his birthday. Each night, Nolan treated himself to some chocolates. There were originally 30 chocolates in the box and after 8 nights, there were 6 chocolates remaining in the box. Write an equation for
C
,
C, in terms of
t
,
t, representing the number of chocolates remaining in the box
t
t days after Nolan's birthday.
Answers
The equation of remaining chocolate C in terms of t is C = 30 - 3t.
What is an equation?A mathematical statement called an equation demonstrates the balance or equality of two expressions. It contains of variables, integers, and mathematical operations and is denoted by the equal symbol (=). Equations may be solved to determine unknown values and are used to express relationships between various quantities. To solve for x in the equation 2x + 3 = 7, for instance, remove 3 from both sides, which gives 2x = 4, then divide both sides by 2, which gives x = 2.
Given that,
Initial number of chocolates in box = 30
Also given that after 8 nights, number of remaining chocolates = 6
Implies that,
In 8 nights, 24 chocolates were treated.
In 1 night, 3 chocolates were treated.
The equation of remaining chocolate C in terms of t can be written as
C = 30 - 3t.
To know more about equation refer to:
brainly.com/question/187506
#SPJ1
35% of what number is 91?
I need step by step too
Answers
Answer:
29.12
Step-by-step explanation:
91 ×35/100 =2912/100
so 29.12
If
f
(
x
)
=
3
5
−
x
+
6
f(x)=3
5−x
+6, what is the value of
f(5), to the nearest tenth (if necessary)?

Answers
Answer:
the answer is f-1(x) = 5 - ln (x - 6)/ln (3) (I guess?)
What is the range of the numbers below?
-3.9
-7.3
4.6
-6.0
0.5
7.2
Answers
What is the slope of the line on the graph below?

Answers
The Boolean expression
A >= B
is equivalent to which of the following expressions?
(A) !(A < B)
(B) !(B >= A)
(C) !(A <= B)
(D) A != B
(E) B >= A
Answers
The Boolean expression A >= B is equivalent to !(A < B) (option A)
To simplify a Boolean expression, use De Morgan's Law.
De Morgan's Law is used to simplify or find the equivalent of a negation of compound expressions.
The principle is:
NOT (A AND B) is equivalent to (NOT A) OR (NOT B)
NOT (A OR B) is equivalent to (NOT A) AND (NOT B)
When the expression involves >, <, = signs, then to simplify the expression, move the not and flip the sign.
! is the symbol of negation or NOT.
Hence,
! (>) becomes <=
! (<) becomes >=
Here are some examples:
!(A > B) is equivalent to (A <= B)
!(A <= B) is equivalent to (A > B)
!(A >= B) is equivalent to (A < B)
!(A == B) is equivalent to (A != B)
!(A != B) is equivalent to (A == B)
!(A < B) is equivalent to (A >= B)
From the above list we can conclude that A >= B is equivalent to !(A < B) (option A)
Learn more about Boolean expression here:
https://brainly.com/question/29619598
#SPJ4
Erika's toy is valued at €450. Its value increased by 10% then decreases by 10% the year after. What is the value of Erika's toy after these two changes?
Answers
Answer:
€445.50-------------------------
Initial value of the toy is €450.
After 10% increase the value is:
€450 + 10% = €450*1.1 = €495After further 10% decrease the value becomes:
€495 - 10% = €495*0.9 = €445.50The final value of the toy is €445.50.
find the values of x and y

Answers
The value of x is 1.75 and y is 5. The solution is obtained using properties of congruent triangles.
What is a congruent triangle?
Two triangles that are congruent will have precisely the same three sides and three angles.
The dimensions of the triangles' sides and angles determine whether two or more triangles are congruent. A triangle's size is determined by its three sides, and its shape by its three angles. Pairs of corresponding sides and corresponding angles in two triangles are said to be equal if they are congruent. They share a similar size and shape. In triangles, there are numerous congruence conditions.
The triangles are congruent by SAS congruency because
AC = CD (Given)
∠ACB = ∠DCE ( Vertically opposite angles)
BC = CE (Given)
Thus, Triangle ABC ≅ Triangle DEC
Since, the triangles are congruent, therefore
⇒AC = CD
⇒4y-6 = 2x+6 ...(1)
Also, BC = CE
⇒3y+1 = 4x
⇒(3y+1)/4 = x ...(2)
Now, substituting the value of x in (1), we get,
⇒4y-6 = 2(3y+1)/4+(6)
⇒4y-6 = (6y+2 +24)/4
⇒16y-24 = 6y+2 +24
⇒10y = 50
⇒y = 5
Now putting the value of y in (2), we get
⇒(3(2)+1)/4 = x
⇒7/4 = x
⇒ x = 1.75
Hence, the value of x is 1.75 and y is 5.
Learn more about congruent triangle from the given link
https://brainly.com/question/29789999
#SPJ1
Select the correct answer from the drop-down menu. In the figure, if CD = 15 cm, then BC ≈ cm.
A) 6.6
B) 11
C) 21.6
D) 34.7

Answers
Answer:
C
Hope this helps!
The length of the side BC is approximately 21.6 cm.
What is Tangent function?Tangent function of an angle in a right angled triangle is defined as the ratio of the opposite side to the adjacent side.
Given a right angled triangle ABC.
We have another smaller right angled triangle ABD.
∠BAD = 180° - (90° + 70°) = 20°
Similarly, ∠BAC = 180° - (90° + 40°) = 50°
Using the definition of tangent function,
tan 20° = BD / AB and tan 50° = BC / AB
Dividing,
tan 20 / tan 50 = BD / BC
Let BD be x.
Now, BC = BD + CD = x + 15
So the equation becomes,
tan 20 / tan 50 = x / (x + 15)
(x + 15) tan (20) = x tan (50)
x (tan 50 - tan 20) = 15 tan 20
Solving,
x = 6.595 cm
So, BC = BD + 15 = 21.595 ≈ 21.6 cm
Hence the length of BC is 21.6 cm.
Learn more about Tangent functions here :
https://brainly.com/question/22043858
#SPJ3
Identify the values of the variables. Give your answers in simplest radical form. HELP!

Answers
The value of the variables in the right triangle are as follows;
\(v = \frac{3\sqrt{2} }{2}\)\(w=\frac{3\sqrt{6} }{2}\)How to find the side of a right tringle?A right triangle is a triangle that has one of its angles as 90 degrees.
The side of a right triangle can be found by using trigonometric ratios.
Therefore, let's find the variable length of the right triangle as follows;
sin 30 = opposite / hypotenuse
sin 30 = v / 3√2
1 / 2 = v / 3√2
cross multiply
3√2 = 2v
divide both sides by 2
v = 3√2 / 2
Let's find the variable w.
cos 30 = adjacent / hypotenuse
cos 30 = w / 3√2
√3 / 2 = w / 3√2
cross multiply
√3 × 3√2 = 2w
3√6 = 2w
divide both sides by 2
w = 3√6 / 2
learn more on right triangle here: https://brainly.com/question/20521641
#SPJ1
Help with graphing rational functions

Answers
Explanation:
Asymptote at x = -2,1
Asymptote is when a number is divided by 0.
Plug in x = -2,1 in the function and both give you a number divided by zero
there are 56 tulips in a flowerbed. the ratio of tulips to daffodils is 3:5. how many tulips and how many daffodils are there in a flowerbed? (Pls answer correctly)
Answers
Answer:
96
Step-by-step explanation:
3x + 5x = 8x.
8 altogether --> 3 tulips and 5 daisies
16 altogether --> 6 tulips and 10 daisies
24 altogether ---> 9 tulips and 15 daisies
etc
etc
48 altogether --> 12 tulips and 20 daisies
96 altogether --> 15 tulips and 25 daisies
Answer:
55 : 56.6666666667
Step-by-step explanation:
3:5 ÷ 3 = 1 : 1.66666666667 + 55= 56.6666666667
who ever answers ths is 52 minutes will get brainlyeiest
Which expression is equivalent to 8-(6r+2)?
-6r+6
2r+2
6r+10
-6r+10
Answers
Answer:
-6r+6
Step-by-step explanation:
Let us expand the expression:
8-(6r+2)=
8-6r-2=
6-6r
OR
-6r+6
I hope this helps! :)
Answer:
6r+6
Step-by-step explanation:
we dont know the variable's number value yet so you can't solve anything with the 6r. We use distribbutive property and solve 8-2 since the 8 is just subtracting everything in the parenthesis. 8-2=6 and you can't do anything with the 6r so the expression would end up as 6r+6.
can someone help please!

Answers
Answer:(6, 5)
Give me brainliest
Here is a table of values for y= f(x).
x -2 -1 0 1 2 3 4 5 6
f(x) 5 6 7 8 9 10 11 12 13
Mark the statements that are true.
A. The domain for f(x) is the set {-2, -1, 0, 1, 2, 3, 4, 5, 6).
B. The range for f(x) is all real numbers.
C. f(-1) = 6
D. f(5) = -2
Answers
The statements that are true are:
A. The domain for f(x) is the set {-2, -1, 0, 1, 2, 3, 4, 5, 6).
C. f(-1) = 6
To determine the truth of each statement, we need to analyze the given table of values for the function f(x).
A. The domain for f(x) is the set {-2, -1, 0, 1, 2, 3, 4, 5, 6).
The x-values listed in the table are -2, -1, 0, 1, 2, 3, 4, 5, and 6. These are the inputs for the function, and therefore, they represent the domain of f(x). Thus, statement A is true.
B. The range for f(x) is all real numbers.
Looking at the y-values listed in the table for f(x), we can see that the range of f(x) is from 5 to 13. It does not include all real numbers, so statement B is false.
C. f(-1) = 6
From the table, we can see that when x = -1, f(x) = 6. Thus, statement C is true.
D. f(5) = -2
There is no entry in the table for f(5), so we cannot determine the value of f(5) from the given information. Therefore, statement D is false.
In conclusion, the true statements are A and C.
For more such questions on statements, click on:
https://brainly.com/question/27839142
#SPJ8
Find the exact surface area of a sphere with a diameter of 13cm
Answers
Answer:
A = 530.929158457
Answer:
Area = 706.8583471
Explanation:
The used law to measure the surface area of the sphere is
\(area \: = 4\pi \: {r}^{2} \)
Where (r) is the radius. The radius is half the diameter, so it will be half 13 which is equal to 7.5. By using this law:
\(4\pi \: {7.5}^{2} = 706.8583471\)
If you like my explanation please give me 5 stars.Which graph represents y = Two-thirdsx + 3?
On a coordinate plane, a line goes through points (negative 2, 0) and (0, 3).
On a coordinate plane, a line goes through points (0, negative 3) and (4, 0).
On a coordinate plane, a line goes through points (negative 3, 1) and (0, 3).
On a coordinate plane, a line goes through points (0, 3) and (3, 1).
Answers
Answer:
c edge 2021;)
Step-by-step explanation:
Hi :), im really struggling with this. Just wanted to know if anyone can explain step by step for me please. Id really appreciate it.

Answers
Answer:
222
Step-by-step explanation:
What I did was calculate the area of each sides of the triangular prism.
For the two triangles:
1/2(6x5)=15 (for 1 triangle, notice there are 2 so -> 30)
For the 2 rectangles:
5x12=60 x2 = 120
For the base:
6x12=72
Add all them together we get 222
I Los siguientes conejos representan la cuarta parte de los que compró Doňa
Rosa para su granja ¿Cuántos fueron los conejos que compró?
Answers
The total number of rabbits bought by Doña Rose for your farm is 4 times the Number of given rabbits.
The number of rabbits bought by Doña Rose for your farm, we need to consider that the given rabbits represent only a quarter of the total number.
the total number of rabbits as 'x'. According to the information, the given rabbits represent a quarter of 'x', which can be expressed as:
Given rabbits = (1/4) * x
To find the value of 'x', we can multiply both sides of the equation by 4
4 * Given rabbits = x
Therefore, the total number of rabbits bought by Doña Rose for your farm is 4 times the number of given rabbits.
the exact value of 'x'. However, we can state that the total number of rabbits bought is four times the number of the given rabbits.
So, if the given rabbits represent 'n' in quantity, the total number of rabbits bought would be 4n.
For more questions on Number .
https://brainly.com/question/26460978
#SPJ8
P is the midpoint of NO and equidistant from MN and MO. If M=8i+3j and no = 4i-5j Find MP
Answers
The position vector of point P, MP, is given by MP = 6i - j.
To find the position vector of point P, which is the midpoint of NO, we can use the midpoint formula.
The midpoint formula states that the midpoint of a line segment with endpoints (x₁, y₁) and (x₂, y₂) is given by:
Midpoint (Mᵖ) = ((x₁ + x₂) / 2, (y₁ + y₂) / 2)
Let's find the position vector of point P using the given information:
Point N: N = 4i - 5j
Point O: O = 8i + 3j
Using the midpoint formula, we can find the coordinates of point P:
x-coordinate of P: (x₁ + x₂) / 2 = (4i + 8i) / 2 = 12i / 2 = 6i
y-coordinate of P: (y₁ + y₂) / 2 = (-5j + 3j) / 2 = -2j / 2 = -j
Therefore, the position vector of point P, MP, is given by:
MP = 6i - j
for such more question on vector
https://brainly.com/question/17157624
#SPJ8
QUESTION IS DOW BELOW 5 POINTS EACH PLEASE HELP PLEASE HELP PLEASE HELP

Answers
The central angle in the circle is ∠DAC,major arc is BED, minor arc is ADC and BC=(5π*BD)/18.
Given that BD is diameter of the circle and angle BAC is 100°.
We are required to find the central angle, major arc, minor arc, m BEC, BC.
Angle is basically finding out the intensity of inclination of something on the surface.
In the circle central angles are many like BAC and CAD. We can write CAD as DAC also.
Major arc of a circle is that arc whose length is larger than all other arcs in the circle.
In our circle the major arc is arc BED.
Minor arc of a circle is that arc whose length is smaller.
In our circle the minor arc is arc ADC.
We know that arc's length is 2πr(Θ/360)
In this way BC=2π*(BD/2)*100/360
=(5π*BD)/18
We cannot find angle BEC.
Hence the central angle in the circle is ∠DAC,major arc is BED, minor arc is ADC and BC=(5π*BA)/18.
Learn more about angles at https://brainly.com/question/25716982
#SPJ1
Set the mean and standard deviation to 0 and 5 , respectively. Approximately 5% of the area under the normal curve lies to the right of 8.2 . Consider what would happen if you were to change the mean to 50 and keep the standard deviation at 5 . Can you predict the new value for which approximately 5% of the area under the normal curve lies to the right of this value? Enter your answer accurate to one decimal place.
Answers
Using z-scores and the normal distribution, it is found that the new value would be of 58.2.
In a normal distribution with mean and standard deviation , the z-score of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
It measures how many standard deviations the measure is from the mean. After finding the z-score, we look at the z-score table and find the p-value associated with this z-score, which is the percentile of X, which is the area to the left of Z under the normal curve.The area to the right of Z is 1 subtracted by the p-value of Z.In this problem:
Mean of 50 and standard deviation of 5, thus \(\mu = 50, \sigma = 5\).Area to the right of 0.05, thus Z with a p-value of 1 - 0.05 = 0.95, thus \(Z = 1.645\).We have to find the value of X, then:
\(Z = \frac{X - \mu}{\sigma}\)
\(1.645 = \frac{X - 50}{5}\)
\(X - 50 = 1.645(5)\)
\(X = 58.2\)
A similar problem is given at https://brainly.com/question/15583760
Help
look at the picture

Answers
\(x7 - 2 \: or \: x \leqslant - 3\)

https://brainly.com/question/20659247 Someone please help I seriously need it just use the link know what here you go if you dont wanna use the link
