Wendell didn't make it in Nashville. Now he only
has $12 in nickels and dimes left to his name-
barely enough to pay for a bus ticket back
home. If Wendell has 3 times as many nickels
as dimes, how many dimes does he have?
Help meee lol
Answers
Answer:
Wendell only has $12 in nickels and dimes
Let Wendell have x dimes
If Wendell has 3 times as many nickels as dimes, how many dimes does he have?
Number of nickels = 3x
dime 10 c
nickel 5c
10x+5*3x = 1200 ( $12=1200 c)
25x = 1200
x= 48 number of dimes
Related Questions
dv A model for the velocity v at time t of a certain object falling under the influence of gravity in a viscous medium is given by the equation = 2- dt to the right, sketch the solutions with the init
Answers
The solution is v = \(e^{\frac{-1}{8}\)(c+\(8e^{\frac{1}{8} }\)).
What is the velocity?
The velocity of an object is its speed and direction of motion. The idea of velocity is crucial in kinematics, the part of classical mechanics that explains the motion of bodies. Velocity is a physical vector quantity that requires both magnitude and direction to define.
Here, we have
Given: A model for the velocity v at time t of a certain object falling under the influence of gravity in a viscous medium is given by the equation: (dv/dt)= 1 - (v/8).
We have the differential equation:
(dv/dt)= 1 - (v/8)
dy/dt + v/8 = 1
v' + v/8 = 1
This is a linear differential equation. We conclude that is
p(t) = 1/8
q(t) = 1
We have the formula
v = \(e^{-\int\limits {p(t)} \, dt }\)(c+∫q(t).\(e^{\int\limits {p(t)} \, dt }\))
Now, we calculate the solution of the given differential equation:
v = \(e^{\int\limits\frac{-1}{8} \, dt\)(c+∫1.\(e^{\int\limits {\frac{1}{8} } \, dt }\))
v = \(e^{\frac{-1}{8}\)(c+\(8e^{\frac{1}{8} }\))
Hence, the solution is v = \(e^{\frac{-1}{8}\)(c+\(8e^{\frac{1}{8} }\)).
To learn more about the velocity from the given link
https://brainly.com/question/25749514
#SPJ4
Work out the volume of the cuboid 4cm 10cm 15cm
Answers
Answer:
600 m³
Step-by-step explanation:
Attached Below
If it helps, mark as brainliest. : )
4
Two of the dozen eggs in a carton
are cracked. About what percent of the
carton is cracked?
Answers
Answer:
am 50%
Step-by-step explanation:
I try my best
Answer:
10%
Step-by-step explanation:
Determine which statistical technique you will employ to measure the quality characteristics of your organization. provide examples to support the rationale.
Answers
To measure the quality characteristics of an organization, one statistical technique that can be employed is Statistical Process Control (SPC).
SPC is a method used to monitor and control processes to ensure they are operating within predetermined limits. It involves the use of control charts to analyze process data and identify any variations that may occur.
SPC provides a visual representation of process performance over time, allowing organizations to identify and address any issues that may affect quality. Control charts, such as the X-bar and R charts or the X-bar and S charts, are commonly used in SPC to monitor the mean and variability of a process.
For example, let's say a manufacturing company wants to measure the quality characteristics of its production line. The company can collect data on key quality indicators, such as product dimensions or defects, at regular intervals. Using SPC, the company can create control charts to track these measurements over time. If the data points fall within the control limits, it indicates that the process is stable and in control. However, if there are any data points outside the control limits or any patterns or trends observed, it may indicate a problem that requires investigation and corrective action.
To know more about Statistical Process Control (SPC), refer here:
https://brainly.com/question/32406711#
#SPJ11
5. Biking at a constant rate, Elise travels
35 miles in 7 hours. If she travels at the
same speed, how far will Elise bike in
9 hours?
A 5 mi
B 44 mi
C 45 mi
D 63 mi
Answers
suppose that 12 different people call you in a week. what is the probability you will get at least one phone call per day (assume 7 days in the week)? use a mc simulation to estimate this probability with a margin of error of 0.005.
Answers
The distance between two buildings is 180 feet.You are standing on the roof of the taller building.You measure the angle of depression of the top and bottom of the shorter building. If the angles are 36.7° and 71.1°, respectively, find
a. the height of the taller building
b. the height of the shorter building
Round your answers to the nearest foot.
Answers
Therefore, the height of the shorter building is \(233.32\) feet, rounded to the nearest foot.
The height of the shorter building can be found using trigonometry. Using the angle of depression of\(36.7°,\) the height of the building can be calculated as:
h = \(180/tan(36.7°) = 180/0.7744 = 233.32 feet\)
Using the angle of depression of 71.1°, the height of the building can be calculated as:
h =\(180/tan(71.1°) = 180/2.5092 = 71.76 feet\)
for such more questions on trigonometry
https://brainly.com/question/25618616
#SPJ11
write and solve a system of linear equations to find the values of $x$ and $y$ . a quadrilateral. the angles of the quadrilateral are 5x degrees, (4y minus 2 )degrees, (13x plus 10 )degrees, and 10y degrees.
Answers
As per the angle sum property of quadrilateral, then values of x is 245 and the value of y is 341
Angle sum property of quadrilateral:
The angle sum property states that the sum of all the angles of the quadrilateral is 360 degree.
Given,
The angles of the quadrilateral are 5x degrees, (4y minus 2 )degrees, (13x plus 10 )degrees, and 10y degrees.
Now we have to write and solve a system of linear equations to find the values of x and y.
While we looking into the given angles, then we get the values
=> 5x°
=> (4y - 2)°
=> (13x + 10)°
=> 10y°
We know that, the sum of all the angles of the quadrilateral is 360°.
So, it ca be written as,
=> 5x° + (4y - 2)° + (13x+ 10)° + 10y° = 360°
=> 18x° + 14y° - 8° = 360°
=> 18x° + 14y° = 354°
When we divide all of them by 2, then we get the equation as,
=> 9x° + 7y° = 177°
Now we have to rewrite the given equation as,
=> 9x° = 177° - 7y°
=> x° = (177° - 7y°)/9
Apply these value on the angles, then we get,
=> 13(177 - 7y)/9 = -10
=> 13(177 - 7y) = 90
=> -7y = -90 - 2301
=> 7y = 2391
=> 341
Then the value of x is
=> 245
To know more about Angle sum property here.
https://brainly.com/question/4316040
#SPJ4
find the zeros of the function f(x)=8x^2 +32
Answers
Answer: no solution
Step-by-step explanation:
\(8x^{2} +32=0\)
Factor out 8
\(8(x^{2} +4)=0\)
no solution
Why?
Think about the graph, \(x^{2}\) shifted up 4 has no zeros, even with a vertical stretch of 8.
The row-echelon form of the augmented matrix of a system of equations is given. Find the solution of the system. FYI it’s not b
Answers
Answer:
c.
Step-by-step explanation:
From the last row in the matrix z = 1.
From the second row:
y + 5z = -4
y = -4 -5(1) = -9.
From the first row:
x + -1 = -3
x = - 3 + 1
x = -2.
to calculate the center line of a control chart you compute the ________ of the mean for every period.
Answers
The centre line of a control chart is calculated by computing the average (mean) of the data for every period.
In control chart analysis, the centre line represents the central tendency or average value of the process being monitored. It is typically obtained by calculating the mean of the data points collected over a specific period. The purpose of the centre line is to provide a reference point against which the process performance can be compared. Any data points falling within acceptable limits around the centre line indicate that the process is stable and under control.
The calculation of the centre line involves summing up the values of the data points and dividing it by the number of data points. This average is then plotted on the control chart as the centre line. By monitoring subsequent data points and their distance from the centre line, deviations and trends in the process can be identified. Deviations beyond the control limits may indicate special causes of variation that require investigation and corrective action. Therefore, the centre line is a critical element in control chart analysis for understanding the baseline performance of a process and detecting any shifts or changes over time.
To learn more about mean refer:
https://brainly.com/question/20118982
#SPJ11
given you have declared an array as int ar[45][14][10][10][43][50]; and you are accessing it at ar[29][1][3][0][17][20]; what is the equivalent single dimensional index?
Answers
The resulting index value represents the position of the desired element in a hypothetical one-dimensional array formed by collapsing all the dimensions of the original multidimensional array into a single dimension.
The equivalent single-dimensional index for accessing the element ar[29][1][3][0][17][20] in the array int ar[45][14][10][10][43][50] can be calculated as follows:
First, we need to determine the number of elements before the desired element in each dimension. Starting from the outermost dimension:
The size of the first dimension is 45, so there are 45 elements in each block of size 14x10x10x43x50.
The size of the second dimension is 14, so there are 14 elements in each block of size 10x10x43x50.
The size of the third dimension is 10, so there are 10 elements in each block of size 10x43x50.
The size of the fourth dimension is 10, so there are 10 elements in each block of size 43x50.
The size of the fifth dimension is 43, so there are 43 elements in each block of size 50.
The size of the sixth dimension is 50.
To calculate the equivalent single-dimensional index, we multiply the number of elements in each dimension by the respective size of the block and sum them all together. In this case, it would be:
Index = (29 * (14 * 10 * 10 * 43 * 50)) + (1 * (10 * 10 * 43 * 50)) + (3 * (10 * 43 * 50)) + (0 * (43 * 50)) + (17 * 50) + 20
To learn more about array click here: brainly.com/question/13261246
#SPJ11
Can you help me on this question Plss??
Answers
it is nonlinear and it is constant
Answer:
Linear; constant
Please help me Thank You!
Answers
Answer:
1=part
2=whole
3=variable
Step-by-step explanation:
here u go
find the indefinite integral by making a change of variables. (hint: let u be the denominator of the integrand. remember to use absolute values where appropriate. use c for the constant of integration.)
Answers
The indefinite integral is: ∫(1/(x^2+1))dx = ln|x^2 + 1| + c, where c is the constant of integration
To find the indefinite integral by making a change of variables, we can use the substitution method. Let u be the denominator of the integrand, so we can write:
∫(1/(x^2+1))dx = ∫(1/u) * (du/dx) dx
To find du/dx, we differentiate both sides of u = x^2 + 1 with respect to x:
du/dx = 2x
Substituting this into our integral, we get:
∫(1/u) * (du/dx) dx = ∫(1/u) * (2x) dx
Now we can make a change of variables by letting f(u) = ln|u|. Using the chain rule, we have:
df/du = 1/u
Substituting this into our integral, we get:
∫(1/u) * (2x) dx = 2∫(df/du) * x dx
Integrating with respect to x, we get:
2∫(df/du) * x dx = x * ln|u| + c
Substituting u = x^2 + 1, we get:
x * ln|u| + c = x * ln|x^2 + 1| + c
Therefore, the indefinite integral is:
∫(1/(x^2+1))dx = ln|x^2 + 1| + c, where c is the constant of integration.
Learn more about indefinite here:
https://brainly.com/question/29059587
#SPJ11
The median weight of a boy whose age is between 0 and 36 months can be approximated by the function w(t)=8.65+1.25t−0.0046t ^2 +0.000749t^3 ,where t is measured in months and w is measured in pounds. Use this approximation to find the following for a boy with median weight in parts a) through c) below. a) The rate of change of weight with respect to time. w ′
(t)=
Answers
Therefore, the rate of change of weight with respect to time is \(w'(t) = 1.25 - 0.0092t + 0.002247t^2.\)
To find the rate of change of weight with respect to time, we need to differentiate the function w(t) with respect to t. Differentiating each term of the function, we get:
\(w'(t) = d/dt (8.65) + d/dt (1.25t) - d/dt (0.0046t^2) + d/dt (0.000749t^3)\)
The derivative of a constant term is zero, so the first term, d/dt (8.65), becomes 0.
The derivative of 1.25t with respect to t is simply 1.25.
The derivative of \(-0.0046t^2\) with respect to t is -0.0092t.
The derivative of \(0.000749t^3\) with respect to t is \(0.002247t^2.\)
Putting it all together, we have:
\(w'(t) = 1.25 - 0.0092t + 0.002247t^2\)
To know more about rate of change,
https://brainly.com/question/30338132
#SPJ11
Find an equation of the line perpendicular to the line 3x+6y=5 and passing through the point (1,3). Write the equation in the standard form.
Answers
The standard form of the equation of a line perpendicular to the line (3x + 6y = 5) and passing through the point (1, 3) is (2x - y = -1)
To determine the equation of a line perpendicular to the line (3x + 6y = 5) and passing through the point (1, 3), we can follow these steps:
1. Obtain the slope of the provided line.
To do this, we rearrange the equation (3x + 6y = 5) into slope-intercept form (y = mx + b):
6y = -3x + 5
y =\(-\frac{1}{2}x + \frac{5}{6}\)
The slope of the line is the coefficient of x, which is \(\(-\frac{1}{2}\)\).
2. Determine the slope of the line perpendicular to the provided line.
The slope of a line perpendicular to another line is the negative reciprocal of the slope of the provided line.
So, the slope of the perpendicular line is \(\(\frac{2}{1}\)\) or simply 2.
3. Use the slope and the provided point to obtain the equation of the perpendicular line.
We can use the point-slope form of a line to determine the equation:
y - y1 = m(x - x1)
where x1, y1 is the provided point and m is the slope.
Substituting the provided point (1, 3) and the slope 2 into the equation, we have:
y - 3 = 2(x - 1)
4. Convert the equation to standard form.
To convert the equation to standard form, we expand the expression:
y - 3 = 2x - 2
2x - y = -1
Rearranging the equation in the form (Ax + By = C), where A, B, and C are constants, we obtain the standard form:
2x - y = -1
To know more about equation of a line refer here:
https://brainly.com/question/29205562#
#SPJ11
If angles a & b are vertical angles and the measure of angle a is 123 degrees and the measure of angle b is 3x, what is the value of x?
Answers
Answer:
x = 41
Step-by-step explanation:
vertical angles are congruent , then
3x = 123 ( divide both sides by 3 )
x = 41
which graph best represents the solution to the following system -3x + y< 1
Answers
Answer:
Step-by-step explanation:
2^45
solve the inequality $\frac{29}{289z<\frac{16}{161}z$. try to solve the problem without doing a lot of messy computations!
Answers
The solution to the given inequality as represented in the task content are; z < - 1.00485413 OR z > 1.00485413.
What is the solution to the given inequality?It follows from the task content that the solution of the given inequality; ( 29 / 289z ) < ( 16 / 161 ) z is to be determined.
Since the given inequality is;
( 29 / 289z ) < ( 16 / 161 ) z
By cross multiplication; we have;
161 × 29 < ( 16z × 289z )
( 161 × 29 ) / ( 16 × 289 ) < z²
1.00973183 < z²
Therefore;
1.00485413 < z. OR. -1.00485413 > z.
Ultimately, z < - 1.00485413 OR z > 1.00485413.
Read more on inequalities;
https://brainly.com/question/25275758
#SPJ1
Miguel glues a ribbon border around the edges of a 5-inch by 8-inch picture to create a frame. What is the total length of ribbon Miguel uses?
Answers
\(\qquad\) ☀️So First – we have to find the perimeter of the frame on which the glue is applied and the length of the ribbon used by Miguel. The perimeter of the frame is the total length of ribbon Miguel uses.
Length of the frame is = 5 inchBreadth of the frame is = 8 inch\(\qquad\)____________________
According to the question:-
\(\qquad\)\( \pink{\bf\longrightarrow Perimeter _{(The \:frame) }= The\: total\: length\: of \:ribbon}\)
The frame is in the rectangular shape, as its length and breadth are different . As we know– Perimeter of the rectangle = 2 ( length + breadth ).\(\qquad\)\( \purple{\bf \longrightarrow Perimeter _{(The \:frame) } = 2 ( length\: of\: the \:frame + breadth \:of \:the\: frame )}\)
\(\qquad\)\( \sf \longrightarrow Perimeter _{(The\: frame) } = 2 ( 5 + 8 ) \)
\(\qquad\)\( \sf \longrightarrow Perimeter _{(The \:frame) }= 2 ( 5 ) + 2 ( 8 ) \)
\(\qquad\)\( \sf \longrightarrow Perimeter _{(The\: frame) }= 10 + 16 \)
\(\qquad\)\( \purple{\bf \longrightarrow Perimeter _{(The \:frame) }= 26\: inch} \)
Henceforth, perimeter of the frame is 26 inch.Therefore,
Perimeter of the frame = The total length of ribbon.So, The total length of ribbon = 26 inch.\(\qquad\)____________________
The Answer will be 26 inch
What's the geometric mean of 4 and 4?
Answers
Answer:
4
Step-by-step explanation:
Brainlest- Pls help me pls thank you sm In advance
Answers
z is 125
y is 70 because interior angles of a triangle add up to 180 so 180-55-55=70.
Hope this helps ya.......n don’t forget the brainliest
Please help fast
,......,,,,
Answers
Answer:
Step-by-step explanation:
-3x + 10 = 5x - 8 Add 8 to both sides
-3x + 10 + 8 = 5x Add 3x to both sides
18 = 8x Divide by 8
18/8 = x
x = 2 3/8
x = 2.375
simplify 6/22 = ?/? please help
Answers
Answer:
3/11
Step-by-step explanation:
divide each side by 2
Answer:
3/11
Step-by-step explanation:
Let's simplify the value,
→ 6/22
→(6 ÷ 2)/(22 ÷ 2)
→ 3/11
Thus, the value is 3/11.
What is the sum -2/3 + (-1 1/6) = -4/6 + (-1 1/6)
Answers
Answer:
i think its 9 1/4
Step-by-step explanation:
You have torn a tendon and is facing surgery to repair it. The surgeon explains the risks to you: infection occurs in 4%4% of such operations, the repair fails in 12%,12%, and both infection and failure occur together in 2%.2%. What percentage of these operations succeed and are free from infection
Answers
The percentage of operations that succeed and are free from infection is 86%.
To determine the percentage of operations that succeed and are free from infection, we need to subtract the probabilities of infection and failure from 100%.
Infection occurs in 4% of the operations.
The repair fails in 12% of the operations.
Both infection and failure occur together in 2% of the operations.
Let's calculate the percentage of operations that succeed and are free from infection:
Percentage of operations with infection = 4%
Percentage of operations with failure = 12%
Percentage of operations with both infection and failure = 2%
Percentage of operations without infection = 100% - 4% = 96%
Percentage of operations without failure = 100% - 12% = 88%
Percentage of operations without infection and failure = 100% - (4% + 12% - 2%) = 86%
To know more about percentage:
https://brainly.com/question/16797504
#SPJ4
Set up and solve a system of equations to solve the problem. Helene invested a total of $1,500 in two simple-interest bank accounts. One account paid 4% annual interest; the other paid 5% annual interest. The total amount of interest she earned after 1 year was $69. Find the amount invested in each account. Helene invested $ in the 4% interest account and $ in the 5% account.
Answers
Answer:
Step-by-step explanation:
x + y = 1,500
y = 1,500 - x
0.04x + 0.05y = 69
0.04x + 0.05(1,500 - x) = 69
0.04x + 75 - 0.05x = 69
-0.01x = -6
x = 600
y = 1,500 - 600 = 900
need the answer no is able to give me the right answer
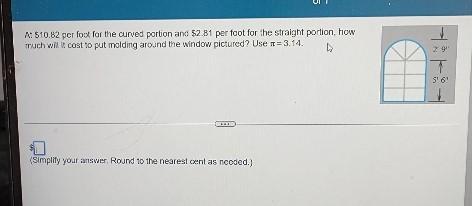
Answers
Given:
The window is divided into a semi-circle and a rectangle.
The radius of the semi-circle is 2' 9''.
The length of the rectangle is 5; 6''.
The cost of put molding for the curved portion is $10.82 per foot.
The cost of put molding for the straight portion is $ 2.81 per foot.
Required:
We need to find the cost to put molding for the window.
Explanation:
Convert inches to feet.
\(We\text{ know that 1 foot =12 inches.}\)Divide 9 inches by 12 to convert inches to feet.
\(9\text{ inches=}\frac{9}{12}feet=\frac{3}{4}feet.\)\(2^{\prime}9^{\prime}^{\prime}=2+\frac{3}{4}=\frac{8+3}{4}=\frac{11}{4}feet.\)\(The\text{ radius of the semi-circle, r =}\frac{11}{4}feet.\)Divide 6 inches by 12 to convert inches to feet.
\(6\text{ inches=}\frac{6}{12}feet=\frac{1}{2}feet.\)\(The\text{ length of the rectangle is, }l=5+\frac{1}{2}feet=\frac{11}{2}feet\)The width of the rectangle is the same as the diameter of the semi-circle.
\(d=2r=2\times\frac{11}{4}=\frac{11}{2}feet.\)\(The\text{ width of the rectangle is, w=}\frac{11}{2}feet.\)Consider the arc length of the semi-circle formula.
\(S=\pi r\)\(\text{ Substitute }r=\frac{11}{4}\text{ and }\pi=3.14\text{ in the formula.}\)\(S=3.14\times\frac{11}{4}\)\(S=8.635feet.\)Multiply the arc length by $10.82 to find the cost of put molding for the curved portion.
\(The\text{ cost of the curved portion=8.635}\times10.82\)\(The\text{ cost of the curved portion=\$ 93.4307.}\)The perimeter of the straight portion is the sum of the three sides of the rectangle.
\(P=l+w+l\)\(Substitute\text{ }l=\frac{11}{2\text{ }}feet\text{ and }w=\frac{11}{2}feet\text{ in the formula.}\)\(P=\frac{11}{2}+\frac{11}{2}+\frac{11}{2}\)\(P=16.5\)Multiply the perimeter by $2.81 to find the cost of put molding for the straight portion.
\(The\text{ cost of the straight portion}=16.5\times2.81\)\(The\text{ cost of the straight portion}=46.365\)The cost to put molding around the window is the sum of the cost of the curved portion and straight portion.
\(The\text{ cost to put molding around the window}=\text{ \$93.4307+ \$}46.365\)\(The\text{ cost to put molding around the window}=\text{ \$139.7957}\)\(The\text{ cost to put molding around the window}=\text{ \$139.80}\)Final answer:
\(The\text{ cost to put molding around the window}=\text{ \$139.80}\)in a certain company 120 of the employees are men. what is the total number of employees if 5 out of every 8 employees are men?
Answers
Answer:
There are 192 employees in the company.
Step-by-step explanation:
Let x be the total number of employees
Use ratio and proportion
\(\frac{120}{x} =\frac{5}{8} \\5x = 120(8)\\5x = 960\\\frac{5x}{5} = \frac{960}{5} \\x = 192\)
x = 192