The coordinates of ADEF are D(-1, 4), E (7,-3), and F (9,5). Write a rule for the translation of ADEF to ADEF. so that the centroid of AD'EF' is
(9,6).
(x,y) -- (x+__y+__) HELP PLEASE
Answers
Answer:
(x,y) -->(x+4,y+4)
Explanation:
The triangle DEF is plotted and shown below:
We can also use the calculation method to find the centroid as done below:
\(\begin{gathered} (x,y)=(\frac{-1+7+9}{3},\frac{4-3+5}{3}) \\ =(\frac{15}{3},\frac{6}{3}) \\ =(5,2) \end{gathered}\)The centroid of △DEF = (5,2)
If the centroid of △D'E'F' is (9,6)
Then, the translation rule is derived below:
\(\begin{gathered} (5+a,2+b)=(9,6) \\ a=4,b=4 \\ \implies(x,y)\to(x+4,y+4) \end{gathered}\)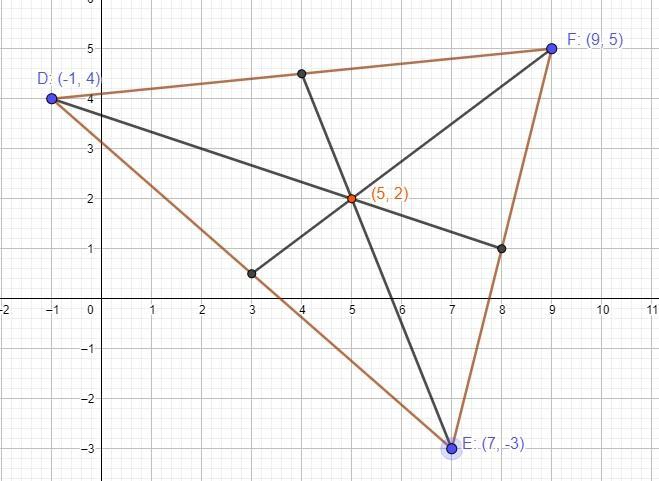
Related Questions
Use interval notation to indicate all real numbers between and including −3 and 5.
Answers
Answer:
[-3,5]
Step-by-step explanation:
Interval notation is a shorthand way of writing and interval of values. To describe an interval, imagine the two endpoints on the number-line. Then, list the two endpoint values, leftmost point from the number-line first, separated by a comma. Lastly, include the appropriate brackets for each endpoint:
Only two brackets total will be used for each interval, a bracket to start it, and one bracket to end it.If a number is included, a square bracket should be used -- either "[" or "]"If the endpoint number is not meant to be included, a 'curved bracket' (which we usually just call a parenthesis) should be used -- either "(" or ")"For our situation, the two endpoints are -3 and 5. -3 is to the left of 5 on the number-line, so -3 should be listed first
\(-3,5\)
Lastly, the directions say "including -3 and 5", so both endpoints should be included.
To include the -3 on the left, we'll use "["To include the 5 on the right, we'll use "]"The final result for the interval is \([-3,5]\)
A portion of a roller coaster track is in the shape of a parabola. Write and graph a quadratic function the models this portion of the roller coaster with a maximum height of 90 feet, represented by a vertex of (25, 90), passing through the point (50, 0).
Answers
The equation of a parabola is: \(y = a(x - h)^2 + k\) where (h,k) represents the vertex.
The equation of the parabola is: \(y = \frac{18}{625}(x - 25)^2 + 90\)
We have:
\((h,k) = (25,90)\) --- the vertex
\((x,y) = (50,0)\) -- one of its point.
Recall that:
\(y = a(x - h)^2 + k\)
Substitute \((h,k) = (25,90)\)
\(y = a(x - 25)^2 + 90\)
To solve for a, we substitute \((x,y) = (50,0)\)
\(0 = a(50 - 25)^2 + 90\)
\(0 = a(25)^2 + 90\)
Collect like terms
\(a(25)^2 = 90\)
\(625a = 90\)
Solve for a
\(a = \frac{90}{625}\)
\(a = \frac{18}{125}\)
Recall that:
\(y = a(x - 25)^2 + 90\)
Hence, the equation of the parabola is:
\(y = \frac{18}{625}(x - 25)^2 + 90\)
See attachment for the graph of \(y = \frac{18}{625}(x - 25)^2 + 90\)
Read more about equation of parabola at:
https://brainly.com/question/4074088

Given rhombus ABCD, find the area if mZABC = 60° and AE = 2.

Answers
The area of the rhombus, obtained from the dimensions, of the diagonals, found from the trigonometric of sines of the angle can be presented as follows;
Area = 8·√3
What is the area of a plane figure?The area of a plane figure is the two dimensional space occupied by the figure on a plane.
The measure of the angle ABC, m∠ABC = 60°
The length of the segment AE = 2 units
The diagonals of a rhombus bisect each other at right angles, and the right angles through which they pass, therefore;
BE = ED, m∠AEB = 90°
m∠ABE = 30°
sin(30°) = AE/AB
sin(30°) = 2/AB
AB = 2/(sin(30°)) = 4
AB = 4
BE = √(4² - 2²) = √(12) = 2·√3
Therefore; AC = 2 + 2 = 4
BD = 2·√3 + 2·√3 = 4·√3
The area of a rhombus = (1/2) × The product of the length of the diagonals
Therefore;
Area of the rhombus = (1/2) × (4·√3) × 4 = 8·√3
The area of the rhombus = 8·√3
Learn more on the area of a rhombus here: https://brainly.com/question/30985956
#SPJ1
What is the value of x? A=55 B=80

Answers
Answer:
x = 45°
Step-by-step explanation:
80° + 55° + x = 180°
135° + x = 180°
x = 45°
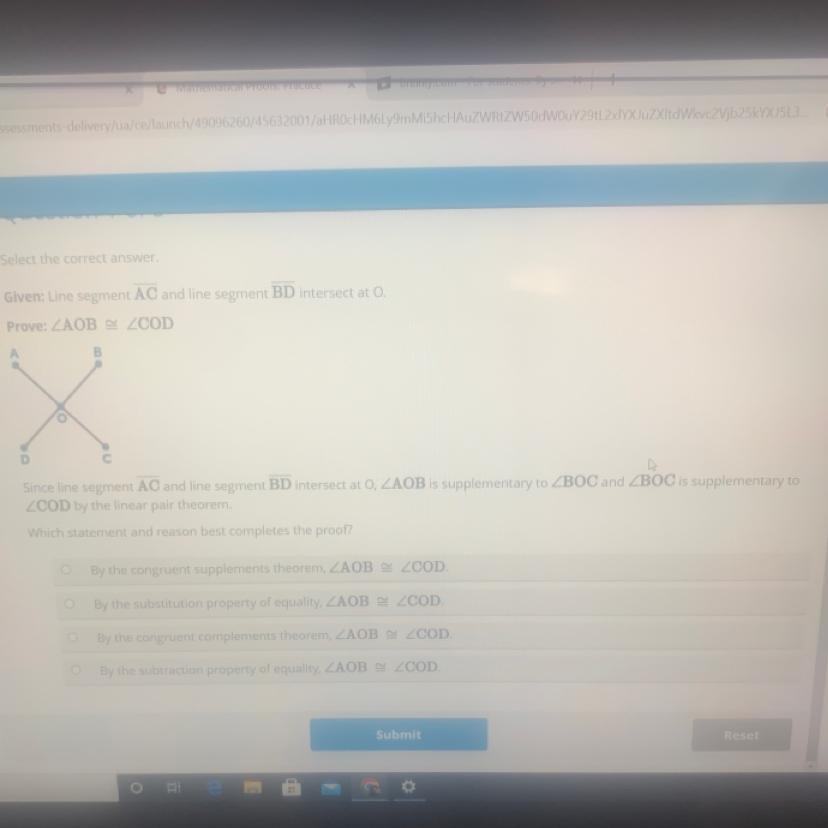
Given: Line segment AC and line segment BD intersect at O.
Prove: ZAOB ZCOD
Since line segment AC and line segment BD intersect at O, ZAOB is supplementary to ZBOC and ZBOC is supplementary to
ZCOD by the linear pair theorem.
Which statement and reason best completes the proof?
ZCOD.
ZCOD.
By the congruent supplements theorem, ZAOB
By the substitution property of equality, ZAOB
By the congruent complements theorem, ZAOBZCOD.
By the subtraction property of equality, ZAOB ZCOD.
Answers
By the substitution property of equality, ∠AOB ≅ ∠COD. Then the correct option is B.
What is an angle?The inclination is the separation seen between planes or vectors that meet. Degrees are another way to indicate the slope. For a full rotation, the angle is 360°.
Supplementary angle - Two angles are said to be supplementary angles if their sum is 180 degrees.
Given: Line segment AC and line segment BD intersect at O.
Prove: ∠AOB ≅ ∠COD
By the supplementary angles property, the equations are given as,
∠AOB + ∠BOC = 180° .....1
∠BOC + ∠COD = 180° ....2
By the substitution property of equality, ∠AOB ≅ ∠COD. Then the correct option is B.
More about the angled link is given below.
https://brainly.com/question/15767203
#SPJ1
Answer: By the congruent complements theorem
Step-by-step explanation: I took the test
A right triangle with a hypotenuse of square root of 61 has an area of 15 square inches. Find the lengths of the other two sides.
Answers
The lengths of the other two sides are 6 inches and 5 inches
Let b represent the base of the right triangle, h represent the height of the right triangle and x represent the hypotenuse.
Since the area of the triangle is 15 in², hence:
Area(A) = (1/2) * base * height
15 = (1/2)bh
bh = 30
b = 30/h (1)
Applying Pythagoras theorem also:
x² = b² + h²
(√61)² = b² + h²
61 = (30/h)² + h²
61 = 900/h² + h²
61h² = 900 + h⁴
h⁴ - 61h² + 900 = 0
h = -6, -5, 5, 6
Since the length cant be negative, hence h = 5 or h = 6
When h = 5; b = 30/5 = 6
When h = 6; b = 30/6 = 5
Therefore the lengths of the other two sides are 6 inches and 5 inches
Find out more at: https://brainly.com/question/2773823
Find the vertex of the graph of the quadratic function f(x)=7x2+14x+10
Answers
Answer:
plazzz get lost bro fast
Explain how to get the answer please

Answers
Answer:
y=8.50x+0.25
Step-by-step explanation:
She/he starts off with 8.50 and throughout the week she can earn 0.25 per joke. We don't know how many times a joke is made so it would be an x.
Answer: b 8.50+0.25 divoide it by 0.25 th3n do the eqathion back words
5/9+ (-4/5)
A. 1/4
B. 11/45
C. -9/14
D. -11/45
PLEASE HELP ILL GIVE BRAINLIST
Answers
Which expression is the additive inverse of 25?
Answers
Answer:it’s actually very simple it’s A.
Step-by-step explanation: anything that is below one is negative that’s how I got my answer.
Answer:the answer is A
Step-by-step explanation:i did the test
I need help with a problem with solving by square roots in quadratic equation.

Answers
To solve for x, first, we add 3 to the given equation:
\(\begin{gathered} 2(x+5)^2-3+3=44+3, \\ 2(x+5)^2=47. \end{gathered}\)Dividing by 2, we get:
\((x+5)^2=\frac{47}{2}.\)Therefore:
\(x+5=\pm\sqrt{\frac{47}{2}}.\)Finally, subtracting 5 we get:
\(x=\pm\sqrt{\frac{47}{2}}-5.\)Answer:
\(x=\operatorname{\pm}\sqrt{\frac{47}{2}}-5.\)Can someone please provide a step-by-step explanation for the answer?
If the universe of discourse is the real numbers, give the truth value of each of the
following propositions:
(a) ∀x∃y(x = y²)
(b) ∀x∃y(x² = y)
(c) ∃x∀y(xy = 0)
(d) ∀x∃y(x + y = 1)

Answers
The Propositions are resulting
(a) ∀x∃y(x = y²) is False
(b) ∀x∃y(x² = y) is True.
(c) ∃x∀y(xy = 0) is True.
(d) ∀x∃y(x + y = 1) is True.
(a) ∀x∃y(x = y²)
This proposition states that for every x, there exists a y such that x is equal to y². To determine the truth value, we need to check if this statement holds true for every value of x.
If we take any positive value for x, we can find a corresponding value of y that satisfies the equation.
For example, if x = 4, then y = 2 satisfies the equation since 4 = 2². Similarly, if x = 9, then y = 3 satisfies the equation since 9 = 3².
Therefore, the proposition (a) is false.
(b) ∀x∃y(x² = y)
For any given positive or negative value of x, we can find a corresponding value of y that satisfies the equation.
For example, if x = 4, then y = 2 satisfies the equation since 4² = 2. Similarly, if x = -4, then y = -2 satisfies the equation since (-4)² = -2.
Therefore, the proposition (b) is true.
(c) ∃x∀y(xy = 0)
The equation xy = 0 can only be satisfied if x = 0, regardless of the value of y. Therefore, there exists an x (x = 0) that makes the equation true for every y.
Therefore, the proposition (c) is true.
(d) ∀x∃y(x + y = 1)
To determine the truth value, we need to check if this statement holds true for every value of x.
If we take any value of x, we can find a corresponding value of y that satisfies the equation.
For example, if x = 2, then y = -1 satisfies the equation since 2 + (-1) = 1. Similarly, if x = 0, then y = 1 satisfies the equation since 0 + 1 = 1.
Therefore, the proposition (d) is true.
Learn more about Proposition here:
https://brainly.com/question/30695879
#SPJ1
Compute 90, 91, 92, 93, 94, and 95. 90 = 1 91 = 9 92 = 81 93 = 729 94 = 6561 95 = 59049 Make a conjecture about the units digit of 9n, where n is a positive integer. If n is even, the units digit of 9n is 1 . If n is odd, the units digit of 9n is 9 . Use strong mathematical induction to prove your conjecture. Submit your proof as a free response. (Submit a file with a maximum size of 1 MB.)
Answers
Answer:
Step-by-step explanation:
First we compute \(9^n\), for \(n = 0,1,2,3,4,5\)
\(9^0=1,9^1=9,9^2=81,9^3=729,9^4=6561,9^5=59049\)
We have the unit digit of \(9^n\), is either 1 or 9
Therefore, the conjecture can be state as follows
Conjecture; the unit of digit of \(9^n\), is 1, when n is even and 9 when n is odd
Let the property p(n) be the formula;
"The unit digit of \(9^n\), is 1 when n is even and 9 when n is odd"↔ P(n)
To show p(n) is true , we will use strong mathematical inductive
Show tgat p(0) and p(1) are true
We have to show the unit digit of \(9^0\) is 1 and \(9^1\) is 9
Since any integer with zero power is one and hence
\(9^0=1\) and \(9^1 = 9\)
Therefore, p(0) and p(1) are true
Show that for al integer \(k\geq 1\), if p(i) is true for all integer i from o through k, then p(k+1) is also true
let k be any integer with \(k \geq 1\) and suppose that for all integer i with \(0 \leq i \leq \leq k\)
the unit digit of \(9^i\) is 1 when is even and 9 when n is odd
we must show that \(9^{k +1}\) equals 1 when n is even and 9 when n is odd
Case I; (k +1 is odd)
in this case k is even and so, by inductive hypothesis, the unit digit of \(9^k\) is 1 and hence there is some non negative integer q such that
\(9^k = 10q + 1\)
now, \(9^{k+1}=9^k(9)\)
= (10q + 1)9
= 90q + 9
= 10.9q + 9
Note that for any non negative integer q , 9q is also an integer and this implies the unit digit of \(9^{k+1}\) is 9
Case II
(k +1 is even)
in this case k is odd and so, by inductive hypothesis, the unit digit of \(9^k\) is 9 and hence there is some non negative integer q such that
\(9^k=10q+9\)
Now,
\(9^{k+1}=9^k.9\\=(10q+9)9\\=90q+81\\=10(9q+8)+1\)
Note that any non negative integer q, 9q + 8 is also an integer and this implies the unit of \(9^{k+1}\) is 1
Since we have proved both the basis and the inductive step of the strong mathematical induction, we conclude that the given statement is true
mations to Determine Similarity
What steps would you take to determine if these
figures are similar? Check all that apply.
Use a scale factor of 2.
Multiply the vertices of polygon ABCD by
O Translate the intermediate image 4 units down.
Perform two different dilations.
Reflect the intermediate image.
Answers
The steps which you would take to determine if these figures are similar include the following:
2. Multiply the vertices of polygon ABCD by 1/2.
5. Reflect the intermediate image.
What is a dilation?In Mathematics and Geometry, a dilation is a type of transformation which typically transforms the dimension (size) or side lengths of a geometric object, without affecting its shape.
Therefore, the dimension or side lengths of the dilated geometric object would be stretched or compressed (shrunk) depending on the scale factor that is applied.
By critically observing the graph representing polygon ABCD, we can logically deduce that a sequence of transformations that would polygon ABCD (pre-image) onto polygon A"B"C"D" (image) is a dilation by a scale factor of 1/2 and a reflection of intermediate image.
Read more on dilation and scale factor here: brainly.com/question/4421026
#SPJ1
Missing information:
The question is incomplete and the complete question is shown in the attached picture.

PLEASE HELP! WILL GIVE BRAINLIEST!

Answers
Answer:
Step-by-step explanation: the best answer is c
Use the binomial squares pattern to multiply (6u3−v)2.
Answers
*☆*――*☆*――*☆*――*☆*――*☆*――*☆*――*☆*――*☆**☆*――*☆*――*☆*――*☆
Answer: 36u^6-12u^3v + v^2
Explanation:
I hope this helped!
<!> Brainliest is appreciated! <!>
- Zack Slocum
*☆*――*☆*――*☆*――*☆*――*☆*――*☆*――*☆*――*☆**☆*――*☆*――*☆*――*☆
Solve -3.5 = x/4for x using the multiplication property of equality.
The operation in the problem is
The inverse operation is
V=X
Answers
\(x=-14\)
Step-by-step explanation:\(-3.5=\frac{x}{4}\)
Swap the sides
\(\frac{x}{4}=-3.5\)
Divide both sides of the equation by the coefficient of variable
\(x=-3.5\times 4\)
Calculate the product or quotient
\(x=-14\)
I hope this helps you
:)
There are 12 chickens.
Every week each chicken lays 3 eggs.
What is the totai number of eggs iaid in 7 weeks?
You must show your working.
Answers
Answer:
252 eggs in 7 weeks
Step-by-step explanation:
\(12 \times 3 = 36 \\ 36 \times 7 = 252\)
What year was the Jamestown settlement established
Answers
Answer:
1607
Step-by-step explanation:
Explain why the value of the sine ratio for an acute angle
of a right triangle must always be a positive value less
than 1.
Answers
The sine is defined as the length of the opposite side divided by the length of the hypotenuse, both of which are positive. Since dividing a positive number by a positive number results in a positive number, the sine must be positive.
Also, since the hypotenuse is the longest side of the triangle, the sine is equal to some positive number less than the length of the hypotenuse being divided by the length of the hypotenuse, resulting in a number less than 1.
find the interior angle sum for each polygon. Tound your answer to the nearest tenth if necessary.

Answers
Given: A regular octagon
To Determine: The interior sum for the given polygon
Solution
The formula for finding the interior angle sum of a polygon is given as
\(\begin{gathered} S_{um\text{ of interior angle of a polygon}}=(n-2)180^0 \\ n=number\text{ of sides of the polygon} \end{gathered}\)An octagon is a polygon with 8 sides
Substitute the value of n = 8 into the formula
\(undefined\)35 POINTS FOR ONE QUESTION!!!!
An old community soccer field, whose area is 600yd2, is enlarged by a scale factor of 9 to create a new outdoor recreation complex to host additional activities for field hockey, football, baseball, and swimming. What is the total area of the new recreation complex?
Answers
Answer:
48 600 yd²Step-by-step explanation:
If a shape is scaled by a certain scale factor then :
the area of the new shape = (the scale factor) times (the area of the original object)
………………………
the new recreation complex was created by enlarging the old community soccer field by a scale factor of 9
Then
The area of the new recreation complex = 9² × 600 = 81×600 = 48 600 yd²
A chemical solution contains 15% alcohol. If there is 54 ml of alcohol,what is the volume of the solution
Answers
In Linear equation, The volume of the solution is 100ml.
What in mathematics is a linear equation?
An algebraic equation with simply a constant and a first-order (linear) component, such as y=mx+b, where m is the slope and b is the y-intercept, is known as a linear equation.
Sometimes, the aforementioned is referred to as a "linear equation of two variables," where x and y are the variables. Equations with power 1 variables are known as linear equations. axe+b = 0 is a one-variable example in which a and b are real numbers and x is the variable.
Let the volume of the solution be represented by x.
Therefore, we can form an equation based on the information given which will be
= 15% × x = 54
15/100 × x = 54.
0.15 × x = 54
0.15x = 54
x = 54/0.54
x = 100 ml
The volume of the solution is 100ml.
Learn more about Linear equation
brainly.com/question/11897796
#SPJ1
Find the length of chord AD

Answers
9514 1404 393
Answer:
AD = 15
Step-by-step explanation:
The products of the segment lengths are the same.
(x -2)(x +7) = 4(2x -1)
x^2 +5x -14 = 8x -4
x^2 -3x -10 = 0
(x -5)(x +2) = 0
The positive solution is x=5.
Chord AD is ...
(x -2) +(x +7) = 2x +5 = 2(5) +5 = 15
Chord AD is 15 units long.
a mathematics professor assigns two problems for homework and knows that the probability of a student solving the first problem is 0.90, the probability of solving the second is 0.45, and the probability of solving both is 0.20. (round your answers to three decimal places.)
Answers
The required probabilities for the given sections of the question are a) P(A|B) = 0.111, b) P(B|A) = 0.059.
Explain conditional probability?The probability of occurrence of any occasion A when one more occasion B corresponding to A has proactively happened is known as contingent likelihood.
According to question:A = occasion of tackling the first problem
B = occasion of tackling the second problem
Given
P(A) = 0.85
P(B) = 0.45
P(A and B) = 0.05
Section (a)
Jed has tackled the subsequent issue. So we're given that occasion B has occurred. We need to track down P(A|B) which is the likelihood of occasion An occurrence given B has occurred.
Utilize the restrictive likelihood equation
P(A|B) = P(A and B)/P(B)
P(A|B) = 0.05/0.45
P(A|B) = 0.111111
P(A|B) = 0.111
Part (b)
Same thought as to some degree (a), yet presently we need to track down P(B|A). We know occasion A has occurred and we need to find the likelihood of occasion B happening in light of A.
P(B|A) = P(B and A)/P(A)
P(B|A) = P(A and B)/P(A)
P(B|A) = 0.05/0.85
P(B|A) = 0.05882
P(B|A) = 0.059
Thus, required probability are a) P(A|B) = 0.111, b) P(B|A) = 0.059.
To know more about conditional probability visit:
brainly.com/question/11899923
#SPJ4
Correct question:
a mathematics professor assigns two problems for homework and knows that the probability of a student solving the first problem is 0.90, the probability of solving the second is 0.45, and the probability of solving both is 0.20. (round your answers to three decimal places.)
(a) Jed has solved the second problem. What is the probability he also solves the first problem? (b) Edna has solved the first problem. What is the probability she also solves the second problem?
Jacob learns that the mass of a new planet found in the solar system is 2,330,000,000,000,000,000,000,000 kilograms. What is the mass represented in scientific notation? A. 2.33 × 1024 kilograms B. 2.33 × 10-24 kilograms C. 2.33 × 1023 kilograms D. 23.3 × 1023 kilograms
Answers
Answer:
2.33 x 10^24 kilograms
Step-by-step explanation:
hope this helps!!
=2.33 × \(10{^{21}\)
scientific notation
= 2.33e21
scientific e notation
= 2.33 × \(10{^{21}\)
engineering notation
= 2.33 × \(10{^{21}\)
21
Order of Magnitude
for scientific and standard forms
two setillion three hundred thirty quintillion
what is canceling fractions like 14/28 ?
Answers
To cancel fractions, find a common factor e.g 14/28. 14 and 28 have a common factor of 2. Then divide both number by the common factor.
14÷2=7 28÷2=14. Find if there's another common factor of both numbers. 7 and 14 have a common factor of 7. 7÷7=1 14÷7=2, Therefore 14/28=1/2
Please mark Brainliest.
Solve for x:
8x - 3 = 5(2x + 1)
A. X=-4
B. x= -2
OC. x=1
D. x = 9
Help quick!!

Answers
Answer:
A. X= -4
Step-by-step explanation:
8x-3=5(2x+1)
8x-3=10×+5
-3=2×+5
-8=2x
x=-4
Answer:
A: x=-4
Step-by-step explanation:
8x - 3 = 5(2x + 1)
8x - 3 = 10x + 5
-3 = 2x + 5
-8 = 2x
x = -4
Select all the polygons that would be used in a net of the solid figure shown.
A triangular pyramid. The base has all three sides equal in length. The pyramid is taller than the width of the base.
right triangle
equilateral triangle
isosceles triangle
rectangle
square

Answers
Answer:
C, definitely two sides are different in the triangle.
A, it looks as if the bottom is a right triangle if you look at it in a different way.
The polygons that would be used in a net isosceles triangle & right triangle
What is Pyramid?A pyramid is a structure whose outer surfaces are triangular and converge to a single step at the top,
As, we need a triangular pyramid whose base has all the three sides equal in length.
We can have a net in the form of isosceles triangle whose two are equal
i.e., two sides are different in the triangle.
and also, bottom with the right angle
i.e., the bottom is a right triangle if you look at it in a different way.
Learn more about this concept here:
https://brainly.com/question/18885675
#SPJ2
Which expression is equivalent to 5(6x + 3y)?
A 11x+3y
B 11x+8y
C 30x+3y
D 30x+15y
Answers
Answer:
The answer is **D. 30x+15y**.
```
5(6x + 3y) = 5*6x + 5*3y = 30x + 15y
```
Step-by-step explanation:
1. Distribute the 5:
```
5(6x + 3y) = (5 * 6x) + (5 * 3y)
```
2. Simplify:
```
5(6x + 3y) = 30x + 15y
```
Therefore, 5(6x + 3y) is equivalent to 30x + 15y.