Suppose you have $75 in your savings account and you save an additional $5 each week. Your friend has $30 in his savings account and saves an additional $10
per week. In how many weeks will you have the same amount of money?
Answers
Answer:
9 weeks
Step-by-step explanation:
5x+75=10x+30
-5x -5x
75=5x+30
-30 -30
45=5x
÷5 ÷5
9=x
x=9
it will take 9 weeks for you and your friend to have the same amount of money in your savings accounts.
To determine the number of weeks it takes for both you and your friend to have the same amount of money in your savings accounts, we need to set up an equation.
Let's denote the number of weeks as 'x'. For you, the amount of money in your savings account after 'x' weeks can be calculated as follows:
Amount of money in your account = $75 + $5x
For your friend, the amount of money in his savings account after 'x' weeks can be calculated as:
Amount of money in your friend's account = $30 + $10x
To find the number of weeks where you both have the same amount of money, we set up the equation:
$75 + $5x = $30 + $10x
Simplifying the equation:
$5x - $10x = $30 - $75
-$5x = -$45
Dividing both sides of the equation by -5 gives us:
x = 9
Therefore, it will take 9 weeks for you and your friend to have the same amount of money in your savings accounts.
Learn more about amount here
https://brainly.com/question/16122476
#SPJ2
Related Questions
Find the equation of a line that passes through the point (4,2) and has a gradient of 5.
Leave your answer in the form y = mx + c
Answers
Answer:
The equation of a line in the slope-intercept form is:
y = 5x - 18
Step-by-step explanation:
The slope-intercept form of the line equation
\(y = mx+b\)
where
m is the slopeb is the y-interceptIn our case, we are given
m = 5Point (4, 2)now substituting m = 5 and (4, 2) in the slope-intercept form of the line equation to determine the y-intercept
y = mx + b
2 = 5(4) + b
20 + b = 2
subtract 20 from both side
20 + b - 20 = 2 - 20
b = -18
now substituting b = -18 and m = 5 in the slope-intercept form of the line equation
y = mx + b
y = 5x + (-18)
y = 5x - 18
Therefore, the equation of a line in the slope-intercept form is:
y = 5x - 18
does anyone know this plz help??
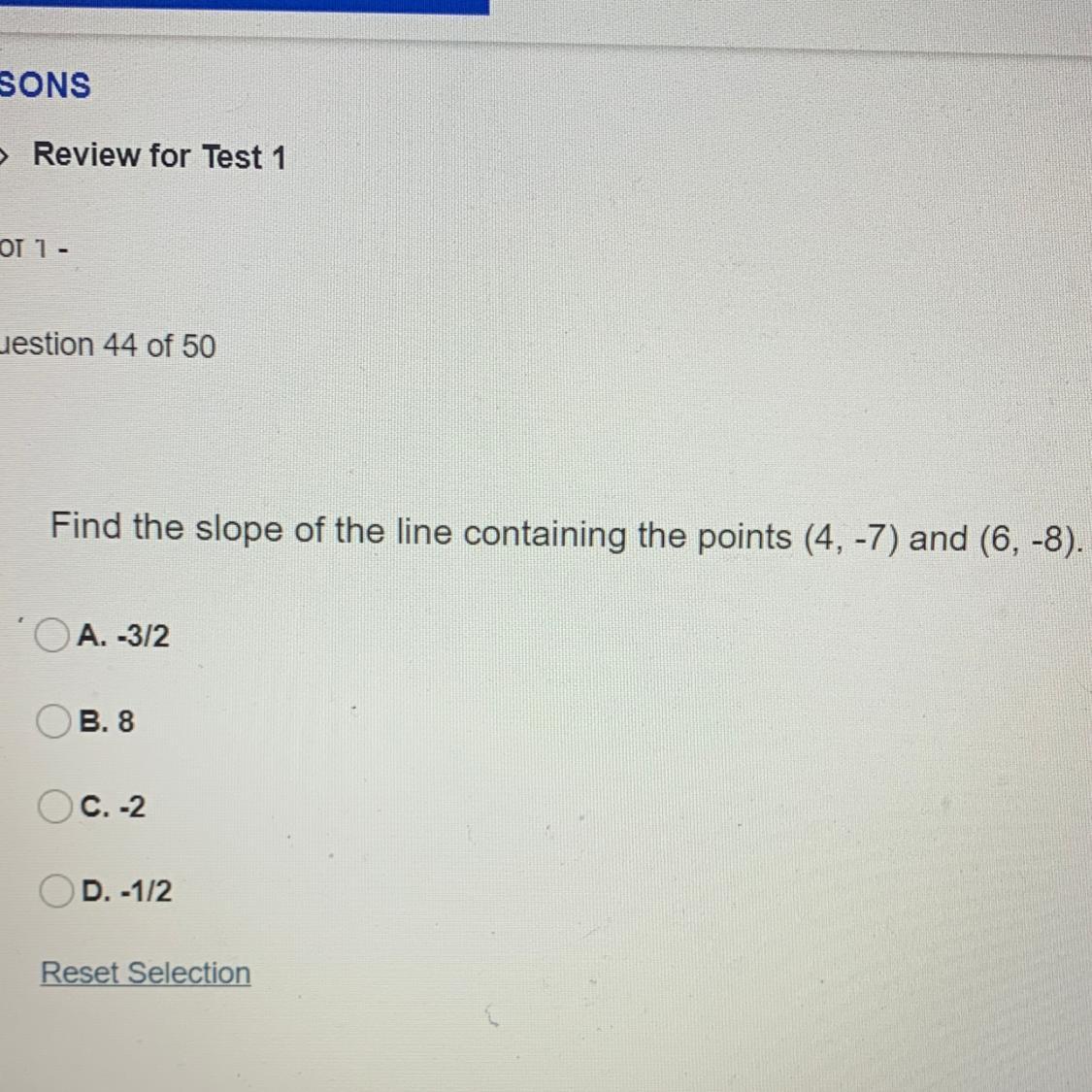
Answers
Answer:
I think the answer is D.
Answer:
m=-1/2
Step-by-step explanation:
slope m=y2-y1/x2-x1
m=-8-(-7)/6-4
m=-1/2
Question 1 (2 x 12 = 24 marks) Analyze and discuss the performance (in Big-O notation) of implementing the following methods over Singly Linked List and Doubly Linked List Data structures: To be submitted through Turnitin.Maximum allowed similaritv is 15% Operation Singly Linked List Doubly Linked List add to start of list Big-O notation Explanation add to end of list Big-O notation Explanation add at given index Big-O notation Explanation
Answers
In analyzing the performance of implementing the given methods over Singly Linked List and Doubly Linked List data structures, we consider the Big-O notation, which provides insight into the time complexity of these operations as the size of the list increases.
Add to Start of List:
Singly Linked List: O(1)
Doubly Linked List: O(1)
Both Singly Linked List and Doubly Linked List offer constant time complexity, O(1), for adding an element to the start of the list.
This is because the operation only involves updating the head pointer (for the Singly Linked List) or the head and previous pointers (for the Doubly Linked List). It does not require traversing the entire list, regardless of its size.
Add to End of List:
Singly Linked List: O(n)
Doubly Linked List: O(1)
Adding an element to the end of a Singly Linked List has a time complexity of O(n), where n is the number of elements in the list. This is because we need to traverse the entire list to reach the end before adding the new element.
In contrast, a Doubly Linked List offers a constant time complexity of O(1) for adding an element to the end.
This is possible because the list maintains a reference to both the tail and the previous node, allowing efficient insertion.
Add at Given Index:
Singly Linked List: O(n)
Doubly Linked List: O(n)
Adding an element at a given index in both Singly Linked List and Doubly Linked List has a time complexity of O(n), where n is the number of elements in the list.
This is because, in both cases, we need to traverse the list to the desired index, which takes linear time.
Additionally, for a Doubly Linked List, we need to update the previous and next pointers of the surrounding nodes to accommodate the new element.
In summary, Singly Linked List has a constant time complexity of O(1) for adding to the start and a linear time complexity of O(n) for adding to the end or at a given index.
On the other hand, Doubly Linked List offers constant time complexity of O(1) for adding to both the start and the end, but still requires linear time complexity of O(n) for adding at a given index due to the need for traversal.
To learn more about Big-O notation visit:
brainly.com/question/30452896
#SPJ11
You are an office manager, and you need to buy a new
printer. You are looking at two options for the printer
model you like. A local electronics store offers the
model for $499.99 plus a 5% sales tax. An online store
offers the same model for $549.99 plus $22.95 for
shipping and no sales tax. You plan to use a coupon
for the online store for 10% off the purchase price
before the shipping fee.
What will be the final price of the better deal?
$472.49
$515.65
$517.94
$524.99
$572.94
Answers
First let's calculate the final price at the electronic store.
499.99*(1+0.05)≈524.99
Now let's calculate the final price online
(549.99+22.95)*(1-0.1)≈515.65
If we compare the two we can see that the online price is cheaper at around 515.65 dollar therefore the second choice is correct.
I hope this helped if you have any questions please ask!
Solve 5x-8y=19 for y.
Answers
Answer:
-19/8+5x/8
Step-by-step explanation:
Answer:
912
Step-by-step explanation:
8x19= 152
152x5= 760
760+152=
John has 7 mice in his lab. He knows a mouse population doubles every month. When can he expect to have 2,625 mice? Please explain.
Answers
Answer:
31 years and 3 months or non
Step-by-step explanation:
the first thought that comes into my mind is
1 month=7 mice
n month= 7×n=2625 mice
n= 2625÷7=375
so it takes him to 375 months = 31 year and 3 months
but putting on a 2nd thought, I noticed that mice and mouse is different species. so there aren't exact answer
The set of life spans of an appliance is normally distributed with a mean Mu = 48 months and a standard deviation Sigma = 8 months. What is the z-score of an appliance that stopped working at 64 months? â€""2 â€""1 1 2.
Answers
The z-score of an appliance that stopped working at 64 months is 2.
z score is used to determine by how many standard deviations the raw score is above or below the mean. It is given by:
\(z=\frac{x-\mu}{\sigma} \\\\where\ x=raw\ score,\mu=mean,\sigma=standard\ deviation\\\)
Given that:
mean = 48, standard deviation = 8 months
For x = 64 months:
\(z=\frac{64-48}{8} \\\\z=2\)
The z-score of an appliance that stopped working at 64 months is 2.
Find out more on z-score at: https://brainly.com/question/25638875
Answer:
D, 2
Step-by-step explanation:
edge
The 3 by 3 grid below shows nine 1 cm × 1 cm 1 cm×1 cm squares and uses 24 cm 24 cm of wire. What length of wire is required for a similar 20 by 20 grid?
Answers
Answer:
Length of wire is required = 840 cm
Step-by-step explanation:
Given:
20 by 20 grid
Find:
Length of wire is required.
Computation:
We know that 20-20 grid required 21 lines.
20 cm vertical and horizontal.
⇒ Length of wire is required = (21 + 21)20 cm
⇒ Length of wire is required = (42)20 cm
⇒ Length of wire is required = 840 cm
What value of [S] as a fraction of KM, is required to obtain 20% Vmax? [S] equals: a. 0.2 KM b. 0.25 KM c. 0.5 KM d. 0.75 KM e. 0.8.
Answers
The fraction of KM that is required to obtain 20% Vmax is [S] = 0.2 KM.
The Michaelis-Menten equation is given by: V = Vmax[S] / (KM + [S])where, V is the velocity of the reaction, Vmax is the maximum velocity of the reaction,[S] is the substrate concentration, and KM is the Michaelis constant of the enzyme.
Substituting V = 0.2V
max and rearranging the equation,
0.2Vmax = Vmax[S] / (KM + [S])
Multiplying both sides by
(KM + [S]),0.2V
max(KM + [S]) = Vmax[S]
Expanding the equation,
0.2VmaxKM + 0.2Vmax[S]
= Vmax[S]0.2VmaxKM
= 0.8Vmax[S]
Dividing both sides by
Vmax,0.2KM = 0.8[S]
Simplifying the equation,
[S] = 0.2 KM / 0.8[S] = 0.25 KM
Therefore, the fraction of KM that is required to obtain 20% Vmax is [S] = 0.2 KM, which is option (a).
Learn more about velocity from:
https://brainly.com/question/80295
#SPJ11
PLEASE ANSWER FAST!!!!! 40 POINTS!!!!

Answers
Answer:
+2
Step-by-step explanation:
Plus cancels minus
There are 4+ and 2 minus
+4 -2 = +2
The result is +2
How do you do this???
Given tan Ф = 4/5, find all other trig functions.
Answers
let : y = Opponent side, x= Adjecent side
and r= hypotenuse
tan = 4/5
y/x = 4/5 => y =4, x=5
so, r = √4²+5²=√16+25=√41
sin = y/r = 4/ √41
cos = x/r = 5/√41
tan = y/x = 4/5
csc = r/y = √41 /4
sec = r/x = √41 /5
cot = x/y = 5/4
Guys can you please help. I dont understand. Thank you. :))))
Lines AB and CD intersect at E. If the measure of angle AEC=5x-20 and the measure of angle BED=x+50, find, in degrees, the measure of angle CEB.
Answers
Answer: 112.5
Step-by-step explanation: When line AB and CD intersect at point E, angle AEC equals BED so you set them equal to each other and find what x is. 5x -20 = x + 50, solving for x, which gives you 17.5. Finding x will tell you what AEC and BED by plugging it in which is 67.5. Angle BED and BEC are supplementary angles which adds up to 180 degrees. So to find angle CEB, subtract 67.5 from 180 and you get 112.5 degrees.
The grades in period 3 algebra 2 have an average of 82 nd vary by 12 percentage points. formulate an absolute value equation that could be used to solve for the maximum and minimum grade.
Answers
The absolute value equation used to solve this problem: | x - 82 | = 12, where x = grade.
What is an absolute value equation?A statement that contains an absolute value is known as an absolute value equation. The absolute value contains the variable of the equation.Now,
Given:
The average of grades = 82%Variation = 12%Let 'x' be the value that gives the value of grades.
The absolute value equation to find the grades will be given by: | x - 82 | = 12
=> x - 82 = ± 12
For maximum value of the grades, x - 82 = 12
=> x = 82 + 12
=> x = 94.
For minimum value of the grades, x - 82 = -12
=> x = 82 - 12
=> x = 70.
Hence, The absolute value equation used to solve this problem: | x - 82 | = 12, where x = grade.
To learn more about absolute value equation, refer to the link: https://brainly.com/question/5012769
#SPJ4
The density of copper is 9.86 g/cm³.
Work out the mass of the solid copper cuboid in kg.
10 cm
3 cm
5 cm
Answers
Answer:
1479 gm
Step-by-step explanation:
V = 10 * 3 * 5 = 150 cm^3
150 cm^3 * 9.86 g / cm^3 = 1479 gm
Help please I need to catch up on work

Answers
Answer:
Step-by-step explanation:
y = -6x + 3
When x = -5 ; y = -6*(-5) + 3 = 30 + 3 = 33
When x = -1 ; y = -6*(-1) +3 = 6 + 3 = 9
When x = 0 ; y = 0+3 = 3
When x = 1 ; y = -6 *1 + 3 = - 6 + 3 = - 3
Answer:
1.33
2.9
3.3
4.-3
Step-by-step explanation:
hope u caught up with your work
A biologist puts an initial population of 500 bacteria into a growth plate. The population is expected to double every 4 hours. Write the equation that will give the expected number of bacteria, n, after x days. (24 hours = 1 day)
Answers
Answer:
\(n = 500e^{-4.1589x}\)
Step-by-step explanation:
Using the exponential growth equation \(N(t) = N_0e^{-kt}\) where;
N₀ is the initial population of the bacteria
N(t) is the population of the bacteria during time t
If a biologist puts an initial population of 500 bacteria into a growth plate, this means that N₀ = 500 at t = 0
\(N(t) = N_0e^{-kt}\\N(t) = 500e^{-k(0)}\\N(t) = 500e^0\\N(t) = 500\)
If the population is expected to double every 4 hours, this means when t = 4, N₀ = 2(500) = 1000
\(N(t) = N_0e^{-kt}\\500 = 1000e^{-4k}\\\frac{500}{1000} = e^{-4k}\\0.5 = e^{-4k}\\ln(0.5) = lne^{-4k}\\ln(0.5) = -4k\\k = \frac{ln0.5}{-4} \\k = 0.1733\)
The equation that will give the expected number of bacteria, n, after x days, can be gotten by substituting N(t) = n and t = x days = 24x hours
\(N(t) = N_0e^{-kt}\\n = N_0e^{-0.1733(24x)}\\n = 500e^{-4.1589x}\)
Hence the equation that will give the expected number of bacteria, n, after x days is \(n = 500e^{-4.1589x}\)
Which expressions have a value of 15 when
S = 15
Answers
what are the answer choices?
The expression S/3 + 10 has the value of 15 when S = 15. Then the correct option is A.
What is the value of the expression?When the relevant components and basic processes of a numerical method are given values, the expression's result is the result of the computation it depicts.
The definition of simplicity is making something simpler to achieve or grasp while also making it a little less difficult.
Let's check all the options, then we have
A. S/3 + 10
If S = 15, then we have
⇒ 15 / 3 + 10
⇒ 5 + 10
⇒ 15
B. S/2 + 10
If S = 15, then we have
⇒ 15 / 2 + 10
⇒ 10 + 10
⇒ 20
C. S + 10
If S = 15, then we have
⇒ 15 + 10
⇒ 15 + 10
⇒ 25
D. - S/3 + 10
If S = 15, then we have
⇒ -15 / 3 + 10
⇒ -5 + 10
⇒ 5
The expression S/3 + 10 has the value of 15 when S = 15. Then the correct option is A.
More about the value of the expression link is given below.
https://brainly.com/question/23671908
#SPJ2
The missing options are given below.
A. S/3 + 10
B. S/2 + 10
C. S + 10
D. - S/3 + 10
What is an equation of a parabola with the given vertex and focus.
Answers
A parabola is a U-shaped curve that can be formed by intersecting a cone with a plane that is parallel to one of its sides.
To find an equation of a parabola given the vertex and focus, we can use the following formula:
For a parabola with vertex (h, k) and focus (h, k + p), the equation is:
(x - h)^2 = 4p(y - k)
where p is the distance from the vertex to the focus.
If the focus is at (h + p, k), then the equation is:
(y - k)^2 = 4p(x - h)
where p is the distance from the vertex to the focus.
what is distance?
In the context of a parabola, the distance is the distance between the vertex and the focus, which is also known as the focal length. It is a constant value that determines the shape and size of the parabola.
To learn more about distance visit:
brainly.com/question/15172156
#SPJ11
What is the image of point 3 4?
Answers
The image of the point (3, 4) with respect to the line x = y is the point that results from reflecting (3, 4) across the line x = y.
To understand this, we first need to understand what it means for a point to be reflected across a line.
Reflection is a transformation that flips a figure across a mirror line or line of reflection. In this case, the line of reflection is x = y. When a point is reflected across a line, the image point is located on the opposite side of the line from the original point, and it is the same distance from the line as the original point.
To find the image of points (3, 4) with respect to x = y, we need to first draw a line x = y in the coordinate plane. Then, we can visualize points (3, 4) on one side of the line and their image on the other side.
When we reflect points (3, 4) across the line x = y, the coordinates of the point will be flipped. The new coordinates will be (4, 3) instead of (3, 4). So the image of the point (3, 4) with respect to x=y is (4,3)
In summary, the image of the point (3, 4) with respect to the line x = y is (4, 3), which is the point that results from reflecting (3, 4) across the line x = y by flipping the coordinates of the point.
To learn more about the distance, visit:
brainly.com/question/15172156
#SPJ4
WILL MARK BRAINLIEST ASAP

Answers
Answer:
4.5 is the answer to k I've done this before
Answer:
3.5
Step-by-step explanation:
19.5 divided 6.5 is 3. 16.5 divided by 5.5 is also 3. Therefore you must
divide 10.5 by 3 (in order to find K) which leads to 3.5.
What is 4x10^-7 ? In write in standard form
Answers
Answer:
0.0000004
Step-by-step explanation:
To write in standard form:
For each power of 10 bigger than 0, we add a zero at the end of the number.
For each power of 10 less than 0, we add a zero before the number(the first one before the decimal point).
In this question:
4x10^(-7)
7 zeros before the number 4, with the first before the decimal point. So
0.0000004
Using simplex method to solve the following problems: (Manual calculations and then confirm your calculation by any software) Max. Z=5A+4B Subject to constraints: 6 A+4 B≤24, A+2 B≤6,−A+B≤1, B≤2, A, B≥0
Answers
Using the simplex method, the maximum value of Z=5A+4B is found to be 19.2 when A=3.6 and B=1.2. The calculations can be confirmed by using any software that solves linear programming problems.
To solve the given linear programming problem using the simplex method, we start by converting the problem into standard form. We introduce slack variables to convert the inequalities into equations.The initial tableau is as follows:
| A | B | S1 | S2 | S3 | S4 | RHS
------------------------------------------
Z | -5 | -4 | 0 | 0 | 0 | 0 | 0
------------------------------------------
S1 | 6 | 4 | 1 | 0 | 0 | 0 | 24
S2 | 1 | 2 | 0 | 1 | 0 | 0 | 6
S3 | -1 | 1 | 0 | 0 | 1 | 0 | 1
S4 | 0 | 1 | 0 | 0 | 0 | 1 | 2
We perform the simplex iterations until the optimal solution is reached. After applying the simplex method, the final tableau is obtained as follows:
| A | B | S1 | S2 | S3 | S4 | RHS
------------------------------------------------------
Z | 0 | 1.8 | 0.2 | -1 | -0.4 | 0.4 | 19.2
------------------------------------------------------
S1 | 0 | 0 | 0 | 1.5 | -1 | 1 | 3
S2 | 1 | 0 | -0.5 | 0.5 | 0.5 | -0.5 | 1.5
A | 1 | 0 | 0.5 | -0.5 | -0.5 | 0.5 | 0.5
S4 | 0 | 0 | 1 | -1 | -1 | 1 | 1
From the final tableau, we can see that the maximum value of Z is 19.2 when A=3.6 and B=1.2. This solution satisfies all the constraints of the problem. The calculations can be verified using any software that solves linear programming problems, which should yield the same optimal solution.
Learn more about linear programming here:- brainly.com/question/30763902
#SPJ11
If two alternate angles are formed on parallel lines, they are said to be______
a. complementary
b. equal
c. supplementary
d. transversal
Answers
Answer:
b
Step-by-step explanation:
equal. where are you from?
If two alternate angles are formed on parallel lines, they are said to be b) equal.
Parallel lines are lines that never intersect, they are at equal distance from each other forever. If passed a transversal between the two parallel line, the angles forming have many relations like corresponding angles, alternate angles, co - interior angles or co - exterior angles.
Given in the question, we have alternate angles, maybe interior of the parallel lines or maybe exterior of the parallel line, but always on the opposite side of transversal. But, alternate angles are always equal to each other.
Thus option b is correct.
Learn more about alternate angles here
https://brainly.com/question/30035264
#SPJ2
Ngela practice the piano for 2 1/2 hour on friday 2 1/3 hour on aturday and unday 3 2/3 hour how long angela practice the piano over the weekend
Answers
Angela practiced piano during the weekend for 6 hours.
According to the question,
Amount Angela spent on Saturday = \(2\frac{1}{3}\)
Amount Angela spent on Sunday = \(3\frac{2}{3}\)
To find out the total amount spent on both days of the weekend =
The amount that Angela spent on Saturday + the amount that Angela spent on Sunday
= \(2\frac{1}{3}\) (otherwise expressed as 7/3) + \(3\frac{2}{3}\) (otherwise expressed as 11/3)
\(= \frac{7}{3} + \frac{11}{3}\)
\(= \frac{7 + 11}{3}\) ( using addition)
= \(\frac{18}{3}\) = 6 hours
Noted, Friday’s value was not added because it didn’t fall on the weekend.
The denominators of both fractions are the alike (3), thereby it was used to factor out the numerators (7) and (11), and subsequently arrive at the final answer which is 6 hours.
So, Angela practiced for 6 hours.
Read more about fractions:
https://brainly.com/question/78672
#SPJ4
Pre-calc. I need help NOW

Answers
Select all of the following that are true about the probability function for a t distribution? a. The t-statistic is the number of standard deviations away from the mean b. The area under thc cunve is 1 c. The t distribution ad standard normal curve look more alike when the random sample size is smaller (<5). d. It is symmetrical e. To calculate thc t-statistic vou need the population standard deviation
Answers
The option b "The area under the curve is 1." and the option d "It is symmetrical" are true about the probability function for a t distribution.
When the sample size is small and the population standard deviation is unknown, the t-distribution is used in statistics.
Option b confirms that the total area under the t-distribution curve is 1, indicating that the sum of probabilities for all possible outcomes is also equal to 1.
Option d confirms the symmetry of the t-distribution, implying that the curve is balanced on both sides of the mean. The mean, median, and mode of a symmetrical distribution are all equal.
To summarize, the t-distribution is a useful tool in statistics when working with small sample sizes because it accounts for the uncertainty in the population standard deviation.
To learn more about t distribution link is here
brainly.com/question/13574945
#SPJ4
WILL MARK BRAINLIEST!
If cos u = 4/5 and tan v = - 12/5 while (3pi)/2 < u < 2pi and pi/2 < v < pi find:
cos2u
Answers
Answer:
Cos 2u = 7/25
Step-by-step explanation:
Here, we want to find the value of cos2u
Using formula, we can rewrite cos 2
Mathematically;
cos 2u = 2cos^2 U - 1
Thus, we have that
cos 2u = 2(4/5)^2 - 1
cos 2u = 2(16/25) - 1
cos 2u = 32/25 - 1
cos 2u = (32-25)/25 = 7/25
i would appreciate help,i dont need an explanation, just the answers. thankyou

Answers
we have
f(x)=7x-1
g(x)=(1/7)(x+1)
Part 1
Find out (fog)(x)
(fog)(x)=f(g(x))=7(1/7)(x+1)-1=x+1-1=x
therefore
(fog)(x)=x
Part 2
Find out (gof)(x)
(gof)(x)=g(f(x))=(1/7)(7x-1+1)=x
therefore
(gof)(x)=x
Part 3
(fog)(x)=(gof)(x)=x
the answer is Yes
What are the quotient and remainder when 3x^(4)-x^(2) is divided by x^(3)-x^(2)+1 ?
Answers
The quotient and remainder when 3x^(4)-x^(2) is divided by x^(3)-x^(2)+1 is x+1 and 2x^2-3, respectively.
To find the quotient and remainder, use long division. First, divide the leading terms of both polynomials. 3x^4 divided by x^3 gives x.
Next, multiply the quotient by the divisor and subtract from the dividend. x(x^3-x^2+1) subtract from 3x^4-x^2 gives x+1.
Finally, divide the remainder by the divisor to get the remainder. x+1 divided by x^3-x^2+1 gives 2x^2-3. Therefore, the quotient and remainder when 3x^(4)-x^(2) is divided by x^(3)-x^(2)+1 is x+1 and 2x^2-3, respectively.
To know more about long division click on below link:
https://brainly.com/question/28824872#
#SPJ11
Find the length and width (in meters) of a rectangle that has the given area and a minimum perimeter. Area: 25 square meters.
a) 5 meters by 5 meters
b) 10 meters by 2.5 meters
c) 6.25 meters by 4 meters
d) 7.5 meters by 3.33 meters
Answers
The length and width of a rectangle with an area of 25 square meters and minimum perimeter is 5 meters by 5 meters.
In order to find the length and width of a rectangle with a given area and minimum perimeter, we need to use the formula for perimeter, which is P = 2L + 2W. We want to minimize the perimeter while still maintaining an area of 25 square meters, so we can use algebra to solve for one variable in terms of the other.
Starting with the formula for area, A = LW, we can solve for L in terms of W by dividing both sides by W: L = A/W. Then, we can substitute this expression for L into the formula for perimeter: P = 2(A/W) + 2W.
To see why this method works, we can think about what we're trying to accomplish. We want to minimize the perimeter of the rectangle while still maintaining a given area. Intuitively, this means we want to "spread out" the rectangle as much as possible while keeping the same amount of area. One way to do this is to make the rectangle as close to a square as possible, since a square has the most even distribution of length and width for a given area. In other words, if we have a fixed area of 25 square meters, the most efficient way to use that area is to make a square with side length 5 meters. To prove this mathematically, we can use the formula for perimeter and the formula for area to express one variable in terms of the other, and then use calculus to find the minimum value of the perimeter. This method gives us the same result as our intuitive approach of making the rectangle as close to a square as possible, and shows that this is indeed the most efficient use of the given area.
To know more about length visit :-
https://brainly.com/question/32060888
#SPJ11