Answers
Answer:
\(V = 97.911in^3\)
Step-by-step explanation:
Given
Shapes: Cube and Cone
Required
Determine the volume
First we calculate the volume of the cube
\(V_1 = l^3\)
Where
l = side length = 5.1
\(V_1 = 5.1^3\)
\(V_1 = 132.651\)
Next, calculate the volume of the cone using:
\(V_2 = \frac{\pi r^2h}{3}\)
Where
h = 5.1
\(r = \frac{1}{2} * Diameter\)
\(r = \frac{1}{2} * 5.1\)
\(r = 2.55\)
So, we have:
\(V_2 = \frac{\pi r^2h}{3}\)
\(V_2 = \frac{\pi * 2.55^2 * 5.1}{3}\)
\(V_2 = \frac{22 * 2.55^2 * 5.1}{7*3}\)
\(V_2 = \frac{729.5805}{21}\)
\(V_2 = 34.74\)
The volume of the figure is:
\(V=V_1 - V_2\)
\(V_1 = 132.651\)
\(V = 132.651 - 34.74\)
\(V = 97.911in^3\)
Related Questions
The unit circle below shows 100∘ and -100∘. Find the values below, rounded to three decimal places if necessary.

Answers
Answer:
sin(100°) = 0.985
sin(-100°) = -0.985
Step-by-step explanation:
In a unit circle, each point (x, y) on the circumference corresponds to the coordinates (cos θ, sin θ), where θ represents the angle formed between the positive x-axis and the line segment connecting the origin to the point (x, y).
Therefore, sin(100°) equals the y-coordinate of the point (-0.174, 0.985), so:
\(\boxed{\sin(100^{\circ}) = 0.985}\)
Similarly, sin(-100°) equals the y-coordinate of the point (-0.174, -0.985), so:
\(\boxed{\sin(-100^{\circ}) = -0.985}\)
In the unit circle the value of sin (100) = 0.985 and the value of sin (-100) = -0.985, in three decimal places.
What is the value of sine of the angles?The value of the sine of the angles is calculated by applying the following formula as follows;
The value of sin (100) is calculated as follows;
sin(100°) corresponds to the y-coordinate of the point (-0.174, 0.985) as given on the coordinates of the unit circle.
sin (100) = 0.985
The value of sin (-100) is calculated as follows;
sin(100°) corresponds to the y-coordinate of the point (-0.174, -0.985), as given on the coordinates of the circle.
sin (-100) = -0.985
Thus, in the unit circle the value of sin (100) = 0.985 and the value of sin (-100) = -0.985, in three decimal places.
Learn more about unit circle here: https://brainly.com/question/30403151
#SPJ1
On the coordinate grid, the graph of y = RootIndex 3 StartRoot negative x minus 1 EndRoot is shown. It is a reflection and translation of y = RootIndex 3 StartRoot x EndRoot. What is the range of the graphed function?
Answers
Using it's concept, it is found that the range of the graphed function \(y = \sqrt[3]{-x -1}\) is of all real values.
What is the range of a function?The range of a function is the set that contains all possible output values for the function.
The parent function \(y = \sqrt[3]{x}\) has all real values as the range, hence any translation of the function, such as \(y = \sqrt[3]{-x -1}\), will have a range of all real values.
More can be learned about the range of a function at https://brainly.com/question/27887009
#SPJ1
I would love for you to help me with my geometry home work
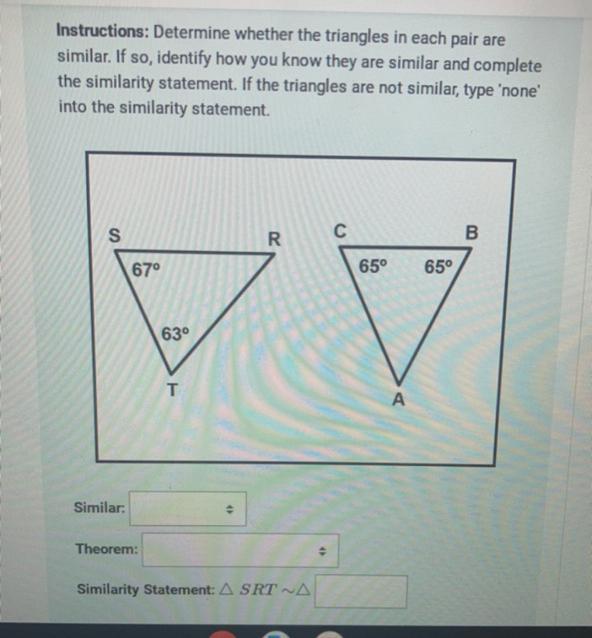
Answers
If two triangles are similar, then their internal angles have the same measure.
Since the internal angles of any triangle must sum to 180º, then the angle R must have a measure of 50º and the angle A must have a measure of 50º.
Nevertheless, notice that angles C and B have a measure of 65º while the angles S and T have measures of 67º and 63º respectively.
Since not all the angles from triangle ABC match those of STR, then, these triangles are not similar.
NO LINKS!! Each graph represents a relation. Determine the domain and range. 2ii

Answers
Answer:
7) Domain: (-∞, ∞)
Range: [-1, ∞)
8) Domain: (-∞, ∞)
Range: (-∞, ∞)
Step-by-step explanation:
Interval notation
( or ) : Use parentheses to indicate that the endpoint is excluded.
[ or ] : Use square brackets to indicate that the endpoint is included.
Domain & Range
The domain is the set of all possible input values (x-values).
The range is the set of all possible output values (y-values).
Question 5From inspection of the graph, the line is continuous.
The arrows either end of the line indicate that the line continues indefinitely in those directions.
Therefore, the domain of the relation is unrestricted: (-∞, ∞)
From inspection of the graph, the minimum y-value is y = -1.
The end behavior of the relation is:
\(y \rightarrow + \infty, \textsf{as } x \rightarrow - \infty\)
\(y \rightarrow + \infty, \textsf{as } x \rightarrow +\infty\)
Therefore, the range of the relation is restricted: [-1, ∞)
Question 6From inspection of the graph, the line is continuous.
The arrows either end of the line indicate that the line continues indefinitely in those directions.
Therefore, the domain of the relation is unrestricted: (-∞, ∞)
The end behavior of the function is:
\(y \rightarrow + \infty, \textsf{as } x \rightarrow - \infty\)
\(y \rightarrow -\infty, \textsf{as } x \rightarrow +\infty\)
Therefore, the domain of the relation is unrestricted: (-∞, ∞)
The directed line segment PR is divided by point Q (0,-1) in a ratio of 4:3. point P (-8,-9)
Draw segment QR, where point R is the endpoint of segment PR.
Answers
The coordinates of R(x₂, y₂) is (6,5)
Given, the directed line segment PR is divided by point Q (0,-1) in a ratio of 4:3. point P (-8,-9)
We know the formula for section formula here
Q(x, y) = ((x₂m + x₁n)/(m + n), (y₂m + y₁n)/(m + n))
Here, (x₁, y₁) = (-8, -9)
(x,y) = (0,-1)
we have to find (x₂, y₂)
(0, -1) = ((4x₂ + (- 24))/(4+3) , (4y₂ + (- 27))/(3+4))
(0, -1) = ((4x₂ - 24)/7 , (4y₂ - 27)/7)
(4x₂ - 24)/7 = 0
4x₂ - 24 =0
4x₂ = 24
x₂ = 6
(4y₂ - 27)/7 = -1
4y₂ - 27 = -7
4y₂ = 20
y₂ = 5
Therefore, the coordinates of R(x₂, y₂) is (6,5)
Learn more about section formula here
https://brainly.com/question/28822588
#SPJ1

x+y+2x=1,x-y+z=-5,3x+y+z=3.
Answers
Hence, The solution is:
x = 1
y = - 2
z = 2
Step-by-step explanation:
Combine Like Terms:3x + y = 1
Combine The Equations:x - y + z = 5
3x + y + z = 3
Eliminate Variables by Method of Elimination:x + y = -1
Unite The System of Linear Equations in Two Variables:x + y = -1
3x + y = 1
Obtain the solution:x = 1
y = -2
Substitute into an original equation:1 - (-2) + z = 5
Evaluate the Value of the Variable:z = 2
Solve a Three Variable System:Hence, The Solution is: x = 1, y = -2, z = 2
I hope this helps you!
nth term for 300,250,200
Answers
The nth term of the arithmetic sequence 300,250,200 is 350-50n if the common ratio is -50
What is a sequence?It is defined as the systematic way of representing the data that follows a certain rule of arithmetic.
We have an arithmetic sequence:
300,250,200
The first term a = 300
Common difference d = 250-300 = -50
nth term:
A(n) = a + (n-1)d
A(n) = 300 + (n-1)(-50)
A(n) = 300 -50n + 50
A(n) = 350—50n
Thus, the nth term of the arithmetic sequence 300,250,200 is 350-50n if the common ratio is -50
Learn more about the sequence here:
brainly.com/question/21961097
#SPJ1
1: 16cm3 = ___________mm3
2: 85000dm3 = _____m3
3:4 L= _____cL
4: 5000 mL= _____ L
5: 25000mm3 = ______cm3
Sorry about the cm3 the number 3 should be up on cm but my phone doesn't have that future.
THANKS FOR THE ANSWER!
its MEASUREMENT!
Answers
1dm is 0.1m so 85000dm is 8500m
1l is 100 cl so 4l is 400cl
1000ml in 1l so 5000ml is 5l
25000mm is 2500cm
Type the integer that makes the following subtraction sentence true for Brainliest!!!

Answers
Answer:
The answer; – 15
\( - 15 \: \: - 19 = - 34\)
I hope I helped you^_^
Answer:
-15
Step-by-step explanation:
34-19=15
CHECK:
-15-19=-34 (correct, and proven)
. Suppose a government agency has a monopoly in the provision of internet connections.
The marginal cost of providing internet connections is 1
2
, whereas the inverse demand
function is given by: p = 1
Answers
The government agency as a monopolist will produce and sell internet connections up to the point where the marginal cost is 1/2. The price will be set at 1, given the perfectly elastic demand function.
In the scenario where a government agency has a monopoly in the provision of internet connections and the inverse demand function is given by p = 1, we can analyze the market equilibrium and the implications for pricing and quantity.
The inverse demand function, p = 1, implies that the market demand for internet connections is perfectly elastic, meaning consumers are willing to purchase any quantity of internet connections at a price of 1. As a monopolist, the government agency has control over the supply of internet connections and can set the price to maximize its profits.
To determine the optimal pricing and quantity, the monopolist needs to consider the marginal cost of providing internet connections. In this case, the marginal cost is given as 1/2. The monopolist will aim to maximize its profits by equating marginal cost with marginal revenue.
Since the inverse demand function is p = 1, the revenue received by the monopolist for each unit sold is also 1. Therefore, the marginal revenue is also 1. The monopolist will produce up to the point where marginal cost equals marginal revenue, which in this case is 1/2.
As a result, the monopolist will produce and sell internet connections up to the quantity where the marginal cost is 1/2. The monopolist will set the price at 1 since consumers are willing to pay that price.
For more such question on monopolist. visit :
https://brainly.com/question/28336090
#SPJ8
2x-1=y
3x-1=y
Consider the system of equations above. Which of the following statements about this system is true?

Answers
Answer:
B; There is only one (x,y) solution and y is negative
Step-by-step explanation:
First, I graphed the two equations. Attached is an image of the equations graphed. Next, I looked for overlapping points. Wherever the two points overlap, there is a solution. When looking at the graph, we can see the lines overlap at only one point, (0,-1). Since y is negative, the answer must be B; there is only one (x,y) solution and y is negative.
If this answer helped you, please leave a thanks!
Have a GREAT day!!!

Ashley has a points card for a movie theater.
• She receives 25 rewards points just for signing up.
• She earns 2.5 points for each visit to the movie theater.
• She needs 45 points for a free movie ticket.
How many visits must Ashley make to earn a free movie ticket?
Answers
Answer:
8
Step-by-step explanation:
45 points for a free movie - 25 points = 20 remaining points needed
20 / 2.5 = 8
She would need 8 visits to earn a free movie ticket.
Answer:
8
Step-by-step explanation:
25+2.5x=45
subtract 25 from each side
2.5x=20
divide both sides by 2.5
x=8
What is the product of 2 linear functions?
Answers
The product of two linear functions having same variables will be a quadratic function where as the The product of two linear functions having different variables will be a linear function.
Linear function is the function whose degree is 1.
Degree of a function is the highest power of the variable of the function.
Let us take two examples.
1. Suppose the two linear functions are -
f(x) = 2x + 3 and g (x) = x + 5
The product of f(x) and g(x) will be
(2x + 3)(x + 5)
=2x (x + 5) + 3 (x + 5)
= 2x² + 10x + 3x + 15
= 2x² + 13x + 15
Here, f(x) and g(x) are the functions having same variables so there product is a quadratic function.
2. Suppose the two linear functions are -
f(x) = 2x + 3 and g (y) = y + 5
The product of f(x) and g(y) will be
(2x + 3)(y + 5)
=2x (y + 5) + 3 (y + 5)
= 2xy + 10x + 3y + 15
Here, f(x) and g(y) are the functions having different variables so there product is a linear function.
To know more about quadratic function here. https://brainly.com/question/27958964#
#SPJ4
HELP PLEASE URGENT!!!
A Ferris wheel is 50 meters in diameter and boarded from a platform that is 4 meters above the ground. The six o'clock position on the Ferris wheel is level with the loading platform. The wheel completes 1 full revolution in 2 minutes. How many minutes of the ride are spent higher than 38 meters above the ground?
answer in minutes.
Answers
The number of minutes spent higher than 38 meters above the ground on the Ferris wheel ride is approximately 1.0918 minutes.
To solve this problem, we need to determine the angular position of the Ferris wheel when it is 38 meters above the ground.
The Ferris wheel has a diameter of 50 meters, which means its radius is half of that, or 25 meters.
When the Ferris wheel is at its highest point, the radius and the height from the ground are aligned, forming a right triangle.
The height of this right triangle is the sum of the radius (25 meters) and the platform height (4 meters), which equals 29 meters.
To find the angle at which the Ferris wheel is 38 meters above the ground, we can use the inverse sine (arcsine) function.
The formula is:
θ = arcsin(h / r)
where θ is the angle in radians, h is the height above the ground (38 meters), and r is the radius of the Ferris wheel (25 meters).
θ = arcsin(38 / 29) ≈ 1.0918 radians
Now, we know the angle at which the Ferris wheel is 38 meters above the ground.
To calculate the time spent higher than 38 meters, we need to find the fraction of the total revolution that corresponds to this angle.
The Ferris wheel completes one full revolution in 2 minutes, which is equivalent to 2π radians.
Therefore, the fraction of the revolution corresponding to an angle of 1.0918 radians is:
Fraction = θ / (2π) ≈ 1.0918 / (2π)
Finally, we can calculate the time spent higher than 38 meters by multiplying the fraction of the revolution by the total time for one revolution:
Time = Fraction \(\times\) Total time per revolution = (1.0918 / (2π)) \(\times\) 2 minutes
Calculating this expression will give us the answer in minutes.
For similar question on diameter.
https://brainly.com/question/28162977
#SPJ8
How many tractors should be produced to incur minimum cost

Answers
For this problem, we are given the function that models the cost of producing a tractor in the function of the number of tractors built. We need to determine the number of tractors we should build to incur the minimum cost.
To solve this problem, we need to find the minimum value for the given function, which happens to be the vertex of the quadratic function. So we have:
\(C(x)=1700-110x+0.2x^2\)\(x_{min}=\frac{-b}{2a}=\frac{-(-110)}{2(0.2)}=\frac{110}{0.4}=275\\\)We need to build 275 tractors.
I’m the standard equation for a line, what does the variable b stand for
Answers
In the standard equation for a line, y = mx + b, the variable b represents the y-intercept of the line.
The standard equation of a line is a way of representing a straight line in a two-dimensional Cartesian coordinate system. It is also called the slope-intercept form.
The slope represents the steepness of the line, while the y-intercept represents the value of y when x is equal to 0.
This form is useful for graphing lines, as well as for finding the equation of a line given its slope and y-intercept.
The y-intercept in the standard equation is the point where the line intersects the y-axis, which means it is the value of y when x = 0.
The slope of the line, represented by "m", determines how steep the line is, while the y-intercept determines where the line crosses the y-axis.
Thus, the b in the standard equation represents y-intercept of the line.
For more details regarding standard equation, visit:
https://brainly.com/question/29059560
#SPJ1
Complete the equation to show how to use the distributive property to express the sum of 30 + 45
with a greatest common factor
30 + 45 = ____ ( ____ + ____ )
Answers
15(2 + 3)
5(6 + 9)
75
1,350
Answers
15(5)
=75
5(6+9)
5(15)
=75
Both answers are equal to 75 so it should be either or
Ginny's account after withdrawal?

Answers
Account balance of Ginny after withdrawal = $ 20 .
Given : Ginny's account balance before withdrawal ie . $ 40
Her withdrawal amount ie . $ 20
To find : account balance after withdrawal
Calculation : Opening balance = $ 40 ie . initially Ginny had $ 40 .
After withdrawal ( taking out ) of $ 20 ,
Ginny has 40 - 20 = $ 20 left .
After adjustment , final amount = $ 20 .
Therefore , account balance of Ginny after withdrawal = $ 20 .
To learn more on word problems follow link :
https://brainly.com/question/21405634
#SPJ9
What is 78 1/3 as a decimal?
Pls help!
Answers
Answer:
78.333333333
Step-by-step explanation:
PLEASE HELP ME ON QUESTION ASAP!!
IF YOU HAVE A TOPIC LIST IN YOUR EXAMS AND IT SAYS AVERAGES AND THE RANGE ARE YOU GOING TO BE HAVING MEAN AND RANGE IN YOUR TEST OR MEAN, RANGE MODE, MIDPOINT BASICALLY ALL OF IT ? IF ANSWERS CORRECT ILL RATE YOU FIVE STARS, GIVE YOU A THANKS AND MAYBE EVEN BRAINLIEST (sorry for caps)
Answers
Answer:
Step-by-step explanation:
Typically yes you need to know
Mean
Median
Mode
and Range
Mean = average, add all numbers then divide by how many
Median = midpoint, middle number. Be sure to list numbers from small to large if there are 2 middle numbers (this happens when there are an even amount), take the average of the 2 middle numbers
Mode = numbers that occurs the most in the list of numbers
Range = This is the largest number minus the smallest number.
look at picture and answer ASAP

Answers
Answer:
its B and A
Step-by-step explanation:
Answer:
its in between the fist and second one cuusing what is given thats what i figured out
Step-by-step explanation:
3 x 36= 108 / 3 x 15 = 45
9 x 12 = 108 / 9 x 5 = 45
6 x 18 = 108 / 6 x 7 = 42
i hope this helps :)
Y (4)
+4y ′′
+4y=0 A general solution with x as the independent variable is y(x)=
Answers
Answer:
Step-by-step explanation:
We can use the method of undetermined coefficients to solve this differential equation. First, we will need to find the solution to the homogeneous equation and the particular solution to the non-homogeneous equation.
For the homogeneous equation, we will use the form y"+ky=0, where k is a constant. We can find the solutions to this equation by letting y=e^mx,
y"=m^2e^mx -> (m^2)e^mx+k*e^mx=0, therefore (m^2+k)e^mx=0
(m^2+k) should equal 0 for the equation to have a non-trivial solution. Therefore, m=±i√(k), and the general solution to the homogenous equation is y=A*e^i√(k)x+Be^-i√(k)*x.
Now, we need to find the particular solution to the non-homogeneous equation. We can use the method of undetermined coefficients to find the particular solution. We will let yp=a0+a1x+a2x^2+.... As the derivative of a sum of functions is the sum of the derivatives, we get
yp″=a1+2a2x....yp‴=2a2+3a3x+....
Substituting the general solution into the non-homogeneous equation, we get
a0+a1x+a2x^2+...+2a2x+3a3x^2+...=Y(4)
So, the coefficient of each term in the expansion of the left hand side should equal the coefficient of each term in the expansion of the right hand side. Since there is only one term on the right hand side, we get the recurrence relation:
a(n+1)=Y(n-2)/n^2
From this relation, we can find all the coefficients in the expansion for the particular solution. Using this particular solution, we can find the total solution to the differential equation as the sum of the homogeneous solution and the particular solution.
Please awnser asap I will brainlist

Answers
Using simultaneous equation, the solution to the system of linear equations are 1223 $10 tickets, 1332 $20 tickets, and 763 $30 tickets were sold.
How many tickets of each kind has been sold?Let's solve the problem step by step.
Let:
x = number of $10 tickets sold
y = number of $20 tickets sold
z = number of $30 tickets sold
From the given information, we can form the following equations:
Equation 1: x + y + z = 3318 (Total number of tickets sold)
Equation 2: y = x + 109 (109 more $20 tickets than $10 tickets were sold)
Equation 3: 10x + 20y + 30z = 61760 (Total sales from ticket sales)
We can use these three equations to solve for the values of x, y, and z.
First, let's substitute Equation 2 into Equation 1:
x + (x + 109) + z = 3318
2x + 109 + z = 3318
2x + z = 3209 (Equation 4)
Now, let's substitute the value of y from Equation 2 into Equation 3:
10x + 20(x + 109) + 30z = 61760
10x + 20x + 2180 + 30z = 61760
30x + 30z = 59580
x + z = 1986 (Equation 5)
We now have a system of equations (Equations 4 and 5) with two variables (x and z). We can solve this system to find the values of x and z.
Multiplying Equation 4 by 30, and Equation 5 by 2, we get:
60x + 30z = 96270 (Equation 6)
2x + 2z = 3972 (Equation 7)
Now, subtract Equation 7 from Equation 6:
(60x + 30z) - (2x + 2z) = 96270 - 3972
58x + 28z = 92298
Simplifying, we have:
29x + 14z = 46149 (Equation 8)
Now, we can solve Equations 5 and 8 simultaneously:
x + z = 1986 (Equation 5)
29x + 14z = 46149 (Equation 8)
Multiplying Equation 5 by 14, and Equation 8 by 1, we get:
14x + 14z = 27804 (Equation 9)
29x + 14z = 46149 (Equation 8)
Now, subtract Equation 9 from Equation 8:
(29x + 14z) - (14x + 14z) = 46149 - 27804
15x = 18345
Divide both sides of the equation by 15:
x = 18345 / 15
x = 1223
Substituting the value of x into Equation 5, we can find z:
1223 + z = 1986
z = 1986 - 1223
z = 763
Now that we have the values of x and z, we can substitute them back into Equation 1 to find y:
1223 + y + 763 = 3318
y + 1986 = 3318
y = 3318 - 1986
y = 1332
Therefore, the solution to the problem is:
x = 1223 (number of $10 tickets sold)
y = 1332 (number of $20 tickets sold)
z = 763 (number of $30 tickets sold)
Learn more on system of linear equation here;
https://brainly.com/question/13729904
#SPJ1
Find the remaining trigonometric ratios. tan(α) = 2, 0<α<π/2the responses they want are:1. sine(α)=_2. cos(α)=_3. cot(α)=_4. sec(α)=_5. csc(α)=_
Answers
Answer:
1. sinα = +2√5/5 2. cosα = +√5/5 3. cotα = +1/2 4. secα = +√5 5. cosecα = +√5/2.
Step-by-step explanation:
1. Since tan(α) = 2 and 1 + cot²α = cosec²α
1 + 1/tan²α = 1/sin²α
1 + 1/2² = 1/sin²α
1 + 1/4 = 1/sin²α
5/4 = 1/sin²α
sinα = ±√(4/5)
sinα = ±2/√5
sinα = ±2√5/5
Since 0<α<π/2, sinα = +2√5/5
2. sin²α + cos²α = 1
(2/√5)² + cos²α = 1
4/5 + cos²α = 1
cos²α = 1 - 4/5
cos²α = 1/5
cosα = ±1/√5
cosα = ±√5/5
Since 0<α<π/2, cosα = +√5/5
3. cotα = 1/tanα = 1/2
Since 0<α<π/2, cotα = +1/2
4. secα = 1/cosα = 1/±1/√5 = ±√5
Since 0<α<π/2, secα = +√5
5. cosecα = 1/sinα = 1/±2/√5 = ±√5/2
Since 0<α<π/2, cosecα = +√5/2
The box plots display data collected when two teachers asked their classes how many pencils they lose in a school year.
A box plot uses a number line from 5 to 47 with tick marks every one unit. The box extends from 8 to 14 on the number line. A line in the box is at 11. The lines outside the box end at 7 and 45. The graph is titled Mr. Johnson's Class, and the line is labeled Number Of Pencils.
A box plot uses a number line from 0 to 51 with tick marks every one unit. The box extends from 12 to 21 on the number line. A line in the box is at 14.5. The lines outside the box end at 0 and 50. The graph is titled Mr. Simpson's Class, and the line is labeled Number Of Pencils.
Which class lost the most pencils overall based on the data displayed?
Mr. Simpson's class; it has a larger median value 14.5 pencils
Mr. Johnson's class; it has a larger median of 11 pencils
Mr. Simpson's class; it has a narrow spread in the data
Mr. Johnson's class; it has a wide spread in the data
Answers
Answer:
A) Mr. Simpson's class; it has a larger median value 14.5 pencils.
Step-by-step explanation:
A box plot is a visual display of the five-number summary:
Minimum value = The value at the end of the left whisker.Lower quartile (Q₁) = The left side of the box.Median (Q₂) = The vertical line inside the box.Upper quartile (Q₃) = The right side of the boxMaximum = The value at the end of the right whisker.From inspection of the box plots (attached), the measures of central tendency (median) and dispersion (range and IQR) are:
Mr Johnson's class:
Median = 11IQR = Q₃ - Q₁ = 14 - 8 = 6Range = max - min = 45 - 7 = 38Mr Simpson's class:
Median = 14.5IQR = Q₃ - Q₁ = 21 - 12 = 9Range = max - min = 50 - 0 = 50In a box plot, the median is a measure of central tendency and tells us the location of the middle value in the dataset. It divides the data into two equal halves, with 50% of the values falling below the median and 50% above it.
The median number of pencils lost in Mr Simpson's class is greater than the median number of pencils lost in Mr Johnson's class. Therefore, Mr. Simpson's class has a larger median value.
The spread of data in a dataset can be measured using both the range and the interquartile range (IQR).
As Mr Simpson's class has a greater IQR and range than Mr Johnson's class, the data in Mr Simpson's class is more spread out than in Mr Johnson's class.
In summary, as Mr Simpson's class has a larger median 14.5 and a wider spread of data, then Mr Simpson's class lost the most pencils overall.

prove if 1-norm less than 2 norm less then infinty norm the there is no c such that inginity norm is less than c 1 norm
Answers
There does not exist a constant C > 0 such that p∞(v) ≤ Cp1(v) for all vectors v in V. Therefore, p1-norm < p2-norm < p∞-norm implies there is no c such that p∞-norm < c p1-norm.
Given two norms, p and q, on a vector space V, we say that p is less than q, written p ≤ q, if there exists a constant C > 0 such that for all vectors v in V,
p(v) ≤ Cq(v)
Now, let's consider the three norms:
The 1-norm: p1(v) = ∑|v_i|
The 2-norm: p2(v) = √(∑v_i^2)
The infinity-norm: p∞(v) = max{|v_i|}
We are given that p1(v) ≤ p2(v) for all vectors v in V and that p2(v) ≤ p∞(v) for all vectors v in V. We want to show that there does not exist a constant C > 0 such that p∞(v) ≤ Cp1(v) for all vectors v in V.
Suppose for the sake of contradiction that such a constant C does exist. Then, for any non-zero vector v in V,
p∞(v) ≤ Cp1(v)
max{|v_i|} ≤ C ∑|v_i|
Since v is non-zero, there exists an index i such that |v_i| > 0. We can divide both sides of the inequality by |v_i| to get:
1 ≤ C ∑|v_j| / |v_i|
Now, since p1(v) ≤ p2(v) for all vectors v in V, we have:
p1(v) = ∑|v_j| ≤ √(∑v_j^2) = p2(v)
So, we can substitute this into the inequality above to get:
1 ≤ C √(∑v_j^2) / |v_i| = Cp2(v) / |v_i|
Finally, since p2(v) ≤ p∞(v) for all vectors v in V, we have:
p2(v) / |v_i| ≤ p∞(v) / |v_i| = 1
So, we have reached a contradiction:
1 ≤ Cp2(v) / |v_i| ≤ C
This contradicts the assumption that C > 0, so there does not exist a constant C > 0 such that p∞(v) ≤ Cp1(v) for all vectors v in V. Therefore, p1-norm < p2-norm < p∞-norm implies there is no c such that p∞-norm < c p1-norm.
To know more about vectors, here
https://brainly.com/question/24256726
#SPJ4
Please help me out!
On a unit test in statistics class, the teacher determines that the mean test grade was 77.5 with a standard deviation of 5.2. What is the test grade, rounded to the nearest whole number, with a z-score of 2.4?
A.65
B.83
C.90
D.95
Answers
Answer:
C: 90
Step-by-step explanation:
Which Statement about 4(x-3) is True?

Answers
Answer: it’s b because if you times that by anything it will always be a product I think
Step-by-step explanation:
A 450m long field is drawn to a scale 1cm to 90m l.find the length of the drawing
Answers
answer: 5cm long
Carla asked students at a lunch table what their main course they liked. Out of these students, 28n liked pizza, 15 liked chicken nuggets, and 8 liked both. what is the probability that a randomly selected student will like pizza but not chicken nuggets?
Answers
The probability that a randomly selected student will like pizza but not chicken nuggets is (28n - 8)/(28n + 7), where 28n is the students who like pizza and 8 is students who like both pizza and chicken nuggets.
To find the probability that a randomly selected student will like pizza but not chicken nuggets.
Let P = the number of students who like pizza but not chicken nuggets
Then, P = the number of students who like pizza - the number of students who like both pizza and chicken nuggets
P = 28n - 8
So, the probability that a randomly selected student will like pizza but not chicken nuggets is:
P(Pizza but not nuggets) = P/(Total number of students)
We can find the total number of students who like either pizza or chicken nuggets by adding the number of students who like pizza and the number of students who like chicken nuggets, and then subtracting the number of students who like both:
Total number of students = 28n + 15 - 8 = 28n + 7
So, the probability that a randomly selected student will like pizza but not chicken nuggets is:
P(Pizza but not nuggets) = P/(Total number of students) = (28n - 8)/(28n + 7)
To learn more about probability please click on below link
https://brainly.com/question/16484393
#SPJ1
