7. IfQ, and Q2 are orthogonal 1 X matrices, show that the product QO2 is orthogonal.
Answers
The product of the two matrices Q₁Q₂ is orthogonal
What i orthogonal matrix?In linear algebra, an orthogonal matrix, or orthonormal matrix, is a real square matrix whose columns and rows are orthonormal vectors. ... {\displaystyle Q^{\mathrm {T} }Q=QQ^{\mathrm {T} }=I,} where QT is the transpose of Q and I is the identity matrix.
It is said to be an orthogonal matrix if its transpose is equal to its inverse matrix, or when the product of a square matrix and its transpose gives an identity matrix of the same order.
If A is an n*n orthogonal matric, then A*A¹ = A¹*A
Therefore A*A¹ = A¹*A = 1
This implies that the product Q₁O₂ is orthogonal.
Learn more about orthogonal matrix on https://brainly.com/question/31053015
#SPJ4
Related Questions
If f(x) = 5 - 2x, find f(-15)
Answers
Answer: 35
Please give me Brainliest
A telecommunication station is designed to receive a maximum of 10 calls per 1/2 second. If the number of calls to the station is modeled as a Poisson random variable with a mean of 9 calls per 1/2 second, what is the probability that the number of calls will exceed the maximum design constraint of the station
Answers
The probability that the number of calls will exceed the maximum design constraint of the station is approximately 0.038, or 3.8%
A telecommunication station is designed to receive a maximum of 10 calls per 1/2 second.
If the number of calls to the station is modeled as a Poisson random variable with a mean of 9 calls per 1/2 second, the probability that the number of calls will exceed the maximum design constraint of the station is approximately 0.038.
We can find this probability using the Poisson distribution formula and solving for the probability of having more than 10 calls in 0.5 seconds.
The Poisson distribution formula is:
P(X = k) = (e^-λ * λ^k) / k!
where X is the random variable (number of calls), λ is the mean of the distribution (9 calls per 0.5 seconds), k is the number of occurrences, e is Euler's number (approximately 2.71828), and k! is the factorial of k.
To find the probability of having more than 10 calls, we need to sum up the probabilities for
k = 11, 12, 13, and so on, up to infinity:
P(X > 10) = 1 - P(X ≤ 10)≈ 1 - 0.962≈ 0.038
Therefore, the probability that the number of calls will exceed the maximum design constraint of the station is approximately 0.038, or 3.8% (rounded to three decimal places).
To know more about probability visit:
https://brainly.com/question/31828911
#SPJ11
Determine what type of transformation is represented help pls
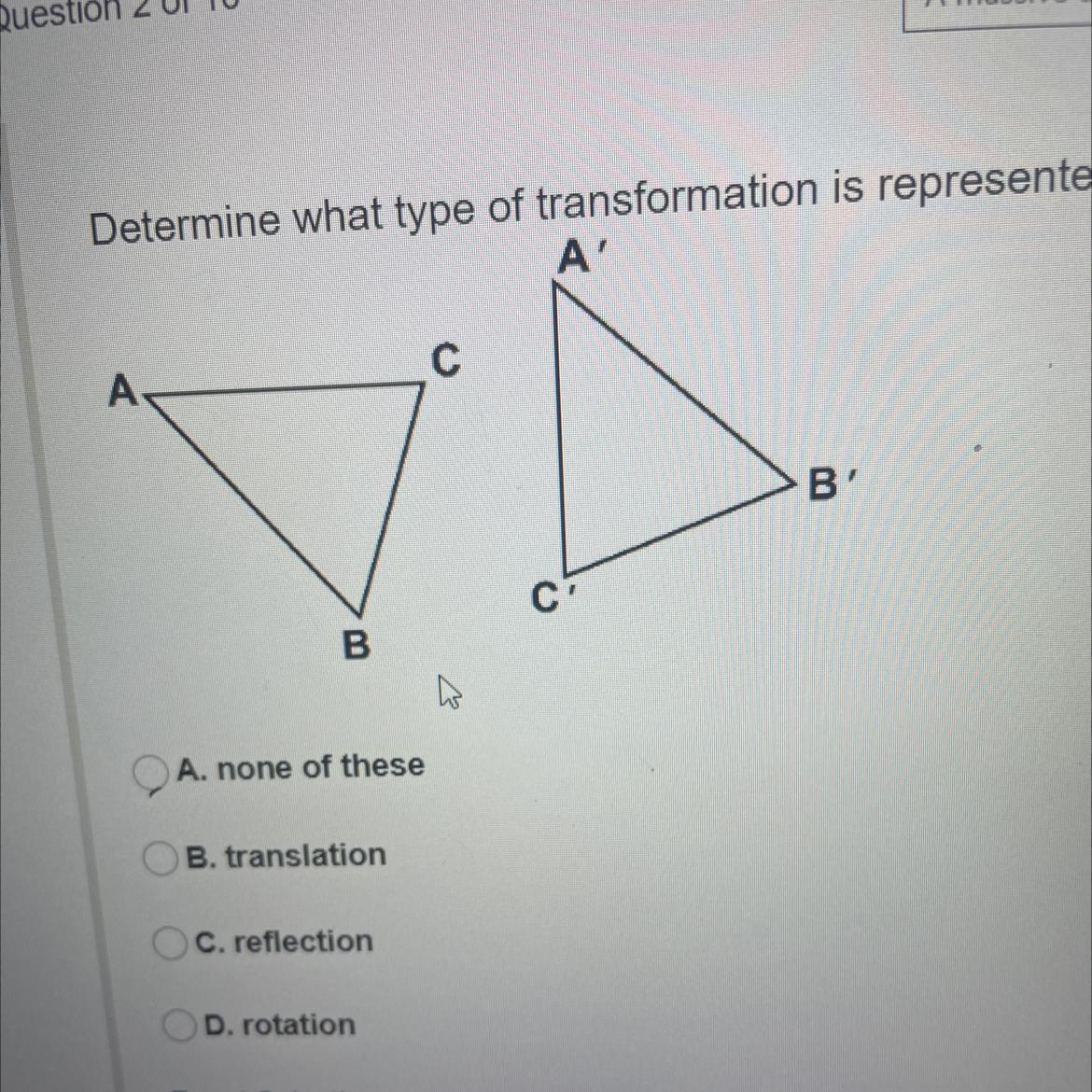
Answers
The type of transformation represented is rotation
Transformation of shapesTransformation techniques is the process of changing the position of an object on the xy-plane.
The transformation technique that we have include;
TranslationReflectionRotationFrom the diagram, you can see that the vertices ABC rotates clockwisely to generate the position A'B'C'. Hence the type of transformation represented is rotation
Learn more on rotation here: https://brainly.com/question/26249005
#SPJ1
Gretel went to the store to buy donuts. She bought 9 boxes of donuts. Since it was the baker’s birthday, he gave out an extra 8 donuts to each box in celebration. In total Gretel bought 117 donuts
a. Equation-
b. Please describe your steps for solving the equation
c. x=
Arnold has 9 boxes of Twix’s. Arnold buys 6 more Twix’s to place in each box. Carson now has 30 Twix’s.
a. Equation-
b. Please describe your steps for solving the equation
c. x=
Max bought 4 packages of oranges. Then she bought 3 more In total she has 31 oranges
a. Equation-
b. Please describe your steps for solving the equation
c. x=
Answers
The equation representing the context is 9(x + 8) = 117 and normally each box contains 5 donuts.
What is an equation?An equation is written in the form of variables and constants separated by the operation of multiplication and division,
An equation states that terms in different forms on both sides of the equality sign are equal.
Multiplication and division do not separate the terms of an equation.
Let, The number of donuts in each box be 'x'
And for the baker’s birthday, it is (x + 8).
Therefore, The equation can be formed as,
9(x + 8) = 117.
9x + 72 = 117.
9x = 45.
x = 5.
So, Normally each box contains 5 donuts.
learn more about equations here :
https://brainly.com/question/10413253
#SPJ1
How do you Form an equation for x and then solve to find the value of x

Answers
9514 1404 393
Answer:
x = 38.2
Step-by-step explanation:
Each of the functions of x represents the measure of an angle in the triangle. You write an equation for x by using what you know about the relationships of angles in a triangle: their sum is 180°.
(2x) +(x -18) +(2x +7) = 180
5x -11 = 180 . . . . . . . collect terms
5x = 191 . . . . . . . . . . add 11
x = 38.2 . . . . . . . . . divide by 5
Can someone help me with the questions in the picture?

Answers
Answer:
\( y = 8 \)
Step-by-step explanation:
Equation of the line that passes through (-2, 8) with a slope of 0, can be written in point-slope form, \( y - y_1 = m(x - x_1) \) and also in slope-intercept form, \( y = mx + b \).
Using a point, (-2, 8) and the slope (m), 0, substitute x1 = -2, y1 = 8 and m = 0 in \( y - y_1 = m(x - x_1) \).
Thus:
\( y - 8 = 0(x - (-2)) \)
\( y - 8 = 0 \)
Rewrite in slope-intercept form
\( y - 8 + 8 = 0 + 8 \) (addition property of equality)
\( y = 8 \)
A size 8 kid's shoe measures 9 2/3 inches. If 5 size 8 shoes are lined end to end, then how many inches will they cover?
Answers
Answer:
its 77 1/3
just do the math with a calculator
Answer: 48 1/3
Step-by-step explanation:
Define Chi square test OR Tests of significance based on Chi-Square. A: -Various tests of significance described previously have mostly applicable to only quantitative data and usually to the data which are approximately normally distributed. It may also happens that we may have data which are not normally Inference: (i) If Z0 ≤ Ze we accept the H0 (ii) If Z0 >Ze we reject the H0 Example: A test of the breaking strengths of two different types of cables was conducted using samples of n1 = n2 = 100 pieces of each type of cable. Do the data provide sufficient evidence to indicate a difference between the mean breaking strengths of the two cables? Use 0.01 level of significance. x = 1925 and sigm = 40 and X2 = 1905, sigma = 30
Answers
The Chi-square test is a statistical test used to determine if there is a significant difference between observed and expected frequencies in categorical data. In this example, the test is used to assess whether there is a significant difference in the mean breaking strengths of two types of cables.
The Chi-square test of significance is employed when dealing with categorical or nominal data. It compares the observed frequencies with the frequencies that would be expected if the variables were independent. In this case, the breaking strengths of the two cables are the variables of interest.
To perform the test, the first step is to define the null hypothesis (H0) and the alternative hypothesis (Ha). In this example, H0 assumes that there is no difference in the mean breaking strengths of the two cables, while Ha suggests that there is a difference.
Next, the test statistic, denoted by X2 (chi-square), is calculated using the formula X2 = Σ[(O - E)²/E], where O represents the observed frequencies and E represents the expected frequencies under the assumption of independence.
To determine the expected frequencies, we need to estimate the means and variances of the breaking strengths. Here, x = 1925 and sigma = 40 for the first cable, and x = 1905 and sigma = 30 for the second cable.
Once the test statistic is calculated, it is compared to a critical value from the Chi-square distribution with degrees of freedom equal to (r - 1)(c - 1), where r is the number of rows and c is the number of columns in the contingency table. The significance level of 0.01 determines the critical value.
If the calculated X2 value is greater than the critical value, we reject the null hypothesis and conclude that there is sufficient evidence to indicate a difference in the mean breaking strengths of the two cables. Conversely, if the calculated X2 value is less than or equal to the critical value, we fail to reject the null hypothesis and conclude that there is no significant difference.
To learn more about chi-square click here: brainly.com/question/32379532
#SPJ11
Select all angle measures for which \sin\theta=-\frac{\sqrt{2}}{2}
Answers
The angles which are equivalent to sin \(\theta\) = √2/2 are,
In the first quadrant sin 45° = √2/2 In the second quadrant sin 225° = √2/2 In the third quadrant sin 135° = √2/2 In the fourth quadrant 315° = √2/2Given sin \(\theta\\\) = √2/2 the theta value is equal to 45° which is present in the first quadrant.
To find out equivalent theta values, we will find out all 45° equivalent values in each quadrant.
In second quadrant equivalent angle = 180° + 45° = 225°.In third quadrant equivalent angle = 180° - 45° = 135°.In fourth quadrant equivalent angle = 360° - 45° = 315°.From the above analysis, the equivalent angles are 45°, 225°, 135° and 315°. So, the option A is correct.
To know more about quadrants,
https://brainly.com/question/28587485
#SPJ1
The given question is missing options. The complete question is,
Select all angle measures for which sin theta= -sqrt2/2
A) 45°, 225°, 135°, and 315°
B) 45°, 225°, 280° and 325°
C)60°, 90°, 225° and 135°
D)75°, 135°, 250° and 315°
2x - 42 = 94
Solve for x
Answers
Answer:
x = 68
Step-by-step explanation:
2x - 42 = 94
Use inverse operations to add 42 to both sides of the equation.
2x - 42 + 42 = 94 + 42
Simplify this to-
2x = 136
Now divide 2x and 136 by two for-
2x/2 = 136/2
Simplify.
x = 68
The answer, then, is x = 68.
I hope this helps ^^
Good luck :]
Find the amount necessary to fund the given withdrawals. 12 Semiannual withdrawals of $950 for 4 years; interest tate is 6.6% compounded semiannually
Answers
In this case, the periodic payment (PMT) is $950, the interest rate (r) is 0.066 (6.6% divided by 100), and the total number of periods (n) is 48.
To find the amount necessary to fund the given withdrawals, we can use the formula for the future value of an ordinary annuity. First, we need to convert the interest rate to a decimal form by dividing it by 100:
6.6% / 100 = 0.066.
Since there are 12 semiannual withdrawals over 4 years, the total number of periods is 12 * 4 = 48.
The formula to find the future value of an ordinary annuity is:
\(FV = PMT * [(1 + r)^n - 1] / r\)
where FV is the future value, PMT is the periodic payment, r is the interest rate per period, and n is the total number of periods.
Plugging in the values into the formula:
\(FV = 950 * [(1 + 0.066)^48 - 1] / 0.066\)
Calculating this expression will give us the amount necessary to fund the given withdrawals.
To know more about the interest, visit:
https://brainly.com/question/8100492
#SPJ11
an angle measures 238 degrees, which is an equivalent coterminal angle measure

Answers
Answer:
c 58
Step-by-step explanation:
Answer:
Step-by-step explanation:
58
Find the exact solution of the initial value problem. Indicate the interval of existence:
y′ = (1+y2) , y(0) = 1
Answers
The exact solution to the initial value problem\(y′= (1+y^2), y(0) = 1 is y + (1/3)y^3 = x + 4/3,\) with an interval of existence of (-∞, ∞).
The given initial value problem is y′ = \((1+y^2),\) with the initial condition y(0) = 1.
To find the exact solution, we can use separation of variables.
1. Start by separating the variables:
\((1+y^2)dy = dx\)
2. Integrate both sides with respect to their respective variables:
∫\((1+y^2)dy\) = ∫dx
3. Integrate the left side:
\(y + (1/3)y^3 = x + C\)
where C is the constant of integration.
4. Substitute the initial condition y(0) = 1:
\(1 + (1/3)(1)^3 = 0 + C\)
1 + (1/3) = C
C = 4/3
5. Substitute the value of C back into the equation:
\(y + (1/3)y^3 = x + 4/3\)
This is the exact solution to the initial value problem.
The interval of existence is determined by the domain of the solution. In this case, the solution is valid for all real numbers, so the interval of existence is (-∞, ∞).
In summary, the exact solution to the initial value problem y′ \(= (1+y^2), y(0) = 1 is y + (1/3)y^3 = x + 4/3,\)with an interval of existence of (-∞, ∞).
know more about real numbers,
https://brainly.com/question/31715634
#SPJ11
.Distribute and combine like terms: −4(7r + 7)
Answers
Answer:
−28r−28
Step-by-step explanation:
−4(7r+7)
=(−4)(7r+7)
=(−4)(7r)+(−4)(7)
In 5-7 complete sentences, write a real world situation that can be modeled by the equation. 3x = 5x + 10
Answers
20 points!!! please please help I don't understand how to do this :( please explain it so that I can do problems similar

Answers
Answer:
Line n
Step-by-step explanation:
We see on the picture that XM=MY
So M is midpoint of the segment XY
Line n passes through midpoint M, so it is the segment bisector of XY
Correct choice is Line n
What percentage of bolivians are catholic? 77% 82% 87% 92%
Answers
According to a survey report in 2018, the percentage of Bolivians that are Catholics is about: A. 77%
Who are the Bolivians?The Bolivians are people from the country, Bolivia. The country Bolivia is described a predominantly Catholic country as a result of its relations between the Church and the state.
Based on a survey report in 2018, about 77% of Bolivians were said to be Catholics.
Learn more about the Bolivians on:
https://brainly.com/question/20556953
#SPJ4
Answer:
1. b- El trópico
2. A- 77%
Step-by-step explanation:
got a 100 and i jus took the test
Find the value of x and y

Answers
Answer:
x=45 degrees
y=45 degrees
Step-by-step explanation:
Answer: y = 50; x = 34
ABCD is a quadrilateral inscribed in the circle
=> ∠ABD = ∠ACD
⇔ x = 34°
and ∠ADB = ∠ACB
we also have:
∠DCE + ∠ DCB = 180°
⇔ 96° + x + ∠ACB = 180°
⇔ ∠ACB = 180 - 96 - x = 180 - 96 - 34 = 50
because ∠ADB = ∠ACB => y = 50°
Step-by-step explanation:
Calculate the value of A please ?

Answers
A=7(4)+13
A= 28+13
A=41
Students are asked to estimate the number of gumballs in a jar. Sam says there are 228 gumballs. In actuality, there are 240 gumballs. What is the percent error
Answers
Answer:
5%
Step-by-step explanation:
Percent error = (actual - estimated) / actual x 100
(240 - 228) / 240 x 100 = 5%
Which expression represents the prime factorization of 276? 7TH Grade Math!
A. 2 x 2 x 3 x 23
B. 2 x 3 x 3 x 23
C. 2 x 2 x 2 x 3 x 23
D. 2 x 2 x 3 x 3 x 23
Answers
Answer:
a
Step-by-step explanation:
Simplify
please answer this question and attach a photo of your solution

Answers
Answer:
7q
Step-by-step explanation:
that is the procedure above

Determine if the relation represents a function. (2,1) (4,-7) (6,0) (4,-1) (2,9)
Answers
Answer:
It isn't a function
Step-by-step explanation:
2 and 4 both have 2 x values, and on a graph, a function cannot have more than 1 x value.
slope -3/8y+-3/4x=12
Answers
Answer:
=
10 − 2 7 - 3
Step-by-step explanation:
5x + 25
25
10
X + 5
Solve for x
Answers
Answer:
can you send a pic of the assignment
Step-by-step explanation:
(i will edit answer)
The functions f and g are defined by fx=8x+33 and gx=2. 1.2x 1
Which function eventually grows faster, f or g? explain how you know.
80 points
Answers
Answer:
To determine which function eventually grows faster, we need to look at their growth rates as x approaches infinity.
For function f(x), the growth rate is 8x, which means that as x gets larger, f(x) gets larger at a rate of 8 times x.
For function g(x), the growth rate is 1.2x, which means that as x gets larger, g(x) gets larger at a rate of 1.2 times x.
Since 8x grows faster than 1.2x as x approaches infinity, we can conclude that function f(x) grows faster than function g(x) in the long run.
Therefore, function f(x) eventually outgrows function g(x).
What is the area?
4 mm
6 mm
6 mm
Answers
which expression is a possible leading term for the polynomial function graphed below? –18x14 –10x7 17x12 22x9
Answers
Among the given expressions, the one that could be the possible leading term for the polynomial function graphed below is -18x¹⁴.
The leading term of a polynomial function is the term containing the highest power of the variable. Among the given expressions, the one that could be the possible leading term for the polynomial function graphed below is -18x¹⁴.
The degree of a polynomial function is the highest degree of any of its terms.
If a polynomial has only one term, then the degree of that term is the degree of the polynomial and is also called a monomial.
For example, consider the given function:Now, observe the degree of the function, which is 14, as the highest exponent of the function is 14.
Thus, the term containing the highest power of the variable x is -18x¹⁴.
Therefore, among the given expressions, the one that could be the possible leading term for the polynomial function graphed below is -18x¹⁴.
To know more about probability visit :-
https://brainly.com/question/1496352
#SPJ11
After several weeks, 18 out of 50 zinnia seeds, 12 out of 30 sunflower seeds, 14 out of 40 marigold seeds grew into plants.
List the names of the plants in order from least percentage to greatest percentage of plants that grew.
Answers
14 out of 40 marigold seeds , 18 out of 50 zinnia seeds , 12 out of 30 sunflower seeds are the names of the plants in the order from least percentage to greatest percentage of the plants that grew
What is percentage?
There is no dimension to percentages. As a result, it is known as a dimensionless number. When we say a number is 50% of anything, we imply that it is 50% of everything.
As in 0.6%, 0.25%, etc., percentages can also be expressed as decimals or fractions. The grades earned in any topic are calculated in terms of percentages in academics. Ram, for instance, scored 78% in his final test. This percentage is derived based on Ram's overall grade point average (GPA) across all disciplines.
10% is equivalent to a fraction of one.
20% is equal to a 1/5 fraction.
25% is equal to a 1/4 fraction.
50% is equal to a 1/2 fraction.
75% is equal to a 1/4 fraction.
90% is equal to a fraction of 9/10.
14 out of 40 marigold seeds = 14/40 x 100 = 35%
18 out of 50 zinnia seeds = 18/50 x 100 = 36%
12 out of 30 sunflower seeds = 12/30 x 100 =40%
Learn more about percentage from the link below
https://brainly.com/question/28269290
#SPJ1
If in δ abc angle a is 50° and angle c is 75°, which triangle is similar to δ abc?.
Answers
The triangle similar to triangle ABC will be the triangle with the corresponding angles as same as 50°, 75°, 55°.
What is triangle?
A triangle is a polygon with three edges and three vertices. The sum of all the angles of a triangle is 180 degrees. Mathematically -
∠x + ∠y + ∠z = 180°
The sum of two sides of a triangle is greater then the third side. Mathematically -
a + b > c
There are different types of triangles such as -
equilateral triangle , scalene triangle , isosceles triangle etc.
Given is a triangle ABC in which angle [A] is 50° and angle [C] is 75°
The third angle of the triangle would be -
A + B + C = 180
50 + 75 + C = 180
C = 180 - 125
C = 55°
The triangle similar to triangle ABC will be the triangle with the corresponding angles as same as 50°, 75°, 55°.
Therefore, the triangle similar to triangle ABC will be the triangle with the corresponding angles as same as 50°, 75°, 55°.
To solve more questions on triangles, visit the link below-
brainly.com/question/25950519
#SPJ1